When sound is transmitted or stored it may need to change form, hopefully without being destroyed.

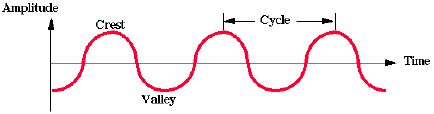
Sound moves fast: in air, at 340 m/sec = 750 miles per hour. Its two important characteristics are Frequency (aka pitch) and Amplitude (aka loudness). Frequency is measured in Hz or cycles per second. Humans can hear frequencies between 20 Hz and 20,000 Hz (20 KHz). Amplitude is measured in deciBels (we will see later that it is approximated with "bit-resolution").
Consider music:
A similar kind of story can be told about visual images (sequences of static images) stored on videotape or DVD and played on your home VCR or DVD player.
Any time signals are transmitted, there will be some degrading of quality:
When we continue to transmit and transform signals, the effect is compounded. Think of the children's game of "telephone." Or think about photocopies of photocopies of photocopies...
This is the transmitted signal:
and this is the received signal (dashed) compared to the transmitted signal:
The horizontal axis here is time. The vertical axis is some physical property of the signal, such as electrical voltage, pressure of a sound wave, or intensity of light.
The degradation may not be immediately obvious, but there is a general lessening of strength and there is some noise added near the second peak.
There doesn't have to be much degradation for it to have a noticeable and unpleasant cumulative effect!
The pictures we saw above are examples of analog signals:
An analog signal varies some physical property, such as voltage, in proportion to the information that we are trying to transmit.
Examples of analog technology:
Analog technology always suffers from degradation when copied.
With a digital signal, we are using an analog signal to transmit numbers, which we convert into bits and then transmit the bits.
A digital signal uses some physical property, such as voltage, to transmit a single bit of information.
Suppose we want to transmit the number 6. In binary, that number is 110. We first decide that, say, "high" means a 1 and "low" means a 0. Thus, 6 might look like:
The heavy black line is the signal, which rises to the maximum to indicate a 1 and falls to the minimum to indicate a 0.
The signals used to transmit bits degrade, too, because any physical process degrades. However, and this is the really cool part, the degraded signal can be "cleaned up," because we know that each bit is either 0 or 1. Thus, the previous signal might be degraded to the following:
Despite the general erosion of the signal, we can still figure out which are the 0s and which are the 1s, and restore it to:
This restoration isn't possible with analog signals, because with analog there aren't just two possibilities. Compare a photocopy of a photocopy ... with a copy of a copy of a copy of a computer file. The computer files are (very probably) perfect copies of the original file.
The actual implementation of digital transmission is somewhat more complex than this, but the general technique is the same: two signals that are easily distinguishable even when they are degraded.
Suppose we have a really bad bit of static, so a 1 turns into a 0 or vice versa. Then what? We can detect errors by transmitting some additional, redundant information. Usually, we transmit a "parity" bit: this is an extra bit that is 1 if the original binary data has an odd number of 1s. Therefore, the transmitted bytes always have an even number of 1s. This is called "even" parity. (There's also "odd" parity.)
How does this help? If the receiver gets a byte with an odd number of 1s, there must have been an error, so we ask for a re-transmission. Thus, we can detect errors in transmission.
You can see some examples of parity using the following form. The parity bit is the last (rightmost) one.
Assuming even parity, what is the parity bit for each of the following:
With some additional mathematical tricks, we can not only detect that a bit is wrong, but which bit is wrong, which means we can correct the value. Thus, we don't even have to ask for re-transmission, we can just fix the problem and go on.
Try it with the following JavaScript form. Type in a number, and it will tell you the binary code to transmit. Then, take the bits and add any single-bit error you want. (In other words, change any 1 to 0 or any 0 to 1.) If you click on "receive," it will tell you which bit is wrong and correct it. If you think I'm cheating, you can type the bits into another browser!
Note: for technical reasons, the parity bits are interspersed with the data bits. In our example, the parity bits are bits 1, 2, 4 and 8, numbering from the left starting at 1. (Notice that those bit position numbers are all powers of two.) So, that means the seven data bits are bits 3, 5, 6, 7, 9, 10, and 11.
transmitbutton
receivebutton.
What if more than one bit is wrong? What if a whole burst of errors comes along? There are mathematical tricks involving larger chunks of bits to check whether the transmission was correct. If not, re-transmission is often possible.
The main point here is that digital transmission and storage of information offers the possibility of perfect (undegraded) copies, because we are only trying to distinguish 1s from 0s, and because of mathematical error checking and error correcting.
 If digital is so much better, can we use digital for music and pictures?
Of course! To do that, we must convert analog to digital, which is done by
sampling.
If digital is so much better, can we use digital for music and pictures?
Of course! To do that, we must convert analog to digital, which is done by
sampling.
Sampling measures the analog signal at different moments in time, recording the physical property of the signal (such as voltage) as a number. We then transmit the stream of numbers. Here's how we might sample the analog signal we saw earlier:
Reading off the vertical scale on the left, we would transmit the numbers 0, 5, 3, 3, -4, ... (The number of bits we need to represent these numbers is the so-called bit-resoluton. In some sense it is the sound equivalent to images' bit-depth.)
Of course, at the other end of the process, we have to convert back to analog, also called "reconstructing" the signal. This is essentially done by drawing a curve through the points. In the following picture, the reconstructed curve is dashed
In the example, you can see that the first part of the curve is fine, but there are some mistakes in the later parts.
The solution to this has two parts:
In the example above, it's clear that we didn't sample often enough to get the detail in the intervals. If we double it, we get the following, which is much better.
In general, finer resolution (bits on the vertical axis) and faster sampling, gets you better quality (reproduction of the original signal) but the size of the file increases accordingly.
How often must we sample? The answer is actually known, and it's called the Nyquist Sampling Theorem (first articulated by Nyquist and later proven by Shannon). Roughly, the theorem says:
Sample twice as often as the highest frequency you want to capture.
For example, the highest sound frequency that most people can hear is about 20 KHz (20,000 cycles per second), with some sharp ears able to hear up to 22 KHz. (Test yourself with this hearing test.) So we can capture music by sampling at 44 KHz (44,000 times per second). That's how fast music is sampled for CD-quality music (actually, 44.1 KHz).
The size of an uncompressed audio file depends on the number of bits per second, called the bit rate and the length of the sound (in seconds).
We've seen that there are two important contributions to the bit rate, namely:
As the sampling rate is doubled, say from 11KHz to 22KHz to 44KHz, the file size doubles each time. Similarly, doubling the bit resolution, say from 8 bits to 16 bits doubles the file size.
As we've seen, the sampling rate for CD-quality music is 44KHz. The bit-resolution of CD-quality music is 16: that is, 16-bit numbers are used on the vertical axis, giving us 216=65,536 distinct levels from lowest to highest. Using this, we can actually calculate the bit rate and the file size:
bit rate (bits per second) = bit-resolution * sampling rate
file size (in bits) = bit rate * recording time
For example, how many bits is 1 second of monophonic CD music?
16 bits per sample * 44000 samples per second * 1 second = 704,000
Therefore, 704,000 / 8 bits per byte = 88,000 bytes ≈ 88 KB
That's 88 KB for one second of music! (Note that there are 1000 bytes in 1KB, so 88000/1000 is 88KB.)
And that's not even stereo music! To get stereo, you have to add another 88KB for the second channel for a total bit-rate of 176KB/second.
An hour of CD-quality stereo music would be:
176 KB/sec * 3600 seconds/hour = 633,600 KB ≈ 634 MB
634 MB is about the size of a CD. In fact, it is not accidental that a CD can hold about 1 hour of music; it was designed that way.
Consider the following form to compute bit-rate and file size. Fill in the missing function definitions.
What are the practical implications of various choices of sampling rate and bit-resolution?
Bandwidth over the internet cannot compete with the playback speed of a CD. Think of how long it would take for that to be downloaded over a slow modem.
So, is it impossible to have sound and movies on your web pages? No, thanks to sound compression techniques. We have seen how GIF and JPG manage to compress images to a fraction of what they would otherwise require. In the case of sound and video, we have some very powerful compression file formats such as Quicktime, AVI, RealAudio and MP3. Read more about the history of MP3 (or history of MP3).
The tradeoffs among different compression formats and different bit rates are explained well in this article on audio formats from the New York Times. (This article is available only on-campus or with a password.)
A discussion of the technology behind these compression schemes is beyond the scope of this course. They are similar in spirit to the JPEG compression algorithm, in that they are lossy compression schemes. That is, they discard bits, but hopefully the bits that least degrade the quality of the music?
Some compression algorithms take advantage of the similarity between two channels of stereo, so adding a second channel might only add 20-30%.
What do you think?
A condensed version of these notes can be found here.
Note that beyond here is information that we think you might find interesting and useful, but which you will not be responsible for. It's for the intellectually curious student.
The error correcting code we saw above may seem a bit magical. And, indeed, the algorithm is pretty clever. But once you see it work, it becomes somewhat mechanical.
Here's the basic idea of this error-correcting code. (This particular code is a Hamming code. The Hamming (7,4) code sends 7 bits, 4 of which are data. The (7,4) code is easy to visualize using Venn diagrams. The general idea is this:
For more detail, see this general algorithm
Solution to the Exercise with Form for Bit-Rate and File Size is here.