PS3: Racket List Recursion
- Due: 11:59pm Wednesday 28 September (no grace period on this!)
- Notes:
- Unlike PS2, this has no reading, but lots of programming (in Racket). Start soon.
- Unlike previous psets, this contains a solo problem (Problem 1). You can start the solo problem right away.
- You should be able to do almost all the rest of the problems after the Tue. Sep. 20 class.
- The problems needn’t be done in order. Feel free to jump around.
- Submission:
- In your yourFullName CS251 Spring 2016 Folder, create a Google Doc named yourFullName CS251 PS3.
- At the top of your yourFullName CS251 PS3 doc, include your name, problem set number, date of submission, and an approximation of how long each problem part took.
- For all parts of all problems, include all answers (derviations, code, etc.) in your PS2 google doc. Please format your evaluation derivations so that they’re easy to read. Format small-step derivations and Racket code using a fixed-width font, like Courier New. You can use a small font size if that helps.
- For Problem 1 (Solo Problem: Recursive Numeric Functions)
- Be sure that all function definitions in
yourAccountName-ps3-solo-functions.rktalso appear in your Google Doc (so that I can comment on them) - Drop a copy of your
yourAccountName-ps3-solo-functions.rktin your~/cs251/drop/ps03drop folder on cs.wellesley.edu.
- Be sure that all function definitions in
- For Problem 3 (Recursive Racket List Functions):
- Be sure that all function definitions in
yourAccountName-ps3-list-functions.rktalso appear in your Google Doc (so that I can comment on them) - Drop a copy of your
yourAccountName-ps3-list-functions.rktin your~/cs251/drop/ps03drop folder on cs.wellesley.edu.
- Be sure that all function definitions in
1. Solo Problem: Recursive Numeric Functions (20 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
This problem involves the following recursive Racket function f:
(define f
(lambda (n)
(if (<= n 2)
n
(+ n (f (quotient n 2)) (f (quotient n 3))))))-
(8 points) Use small-step semantics to derive the evaluation of
(f 17). To keep the size of your derivation manageable, use the same conventions used in small-step derivations in PS2 Problem 5 Sum Fun. In particular:-
Use the notation λ_f as an abbreviation for the
lambdaexpression(lambda (n) (if (<= n 2) n (+ n (f (quotient n 2)) (f (quotient n 3)))))) -
Use ⇒* to show only the most important steps of the derivation.
Also note that
(quotient a b)performs an integer division ofabyb. For example(quotient 11 2)is5and(quotient 11 4)is2. -
-
(1 point) How many times is
fcalled in the evaluation of(f 17)? -
(1 point) What is the maximum stack depth (measured in terms of maximum number of nested
+operations) in the evaluation of(f 17)? -
(5 points) Define a recursive Racket function named
num-f-callsthat takes a single integer argumentnand returns the number of times that the functionfis called in the evaluation of(f n). Notes:-
Define the
num-f-callsfunction in a new file namedyourAccountName-ps3-solo-functions.rktthat you create in Dr. Racket. -
(num-f-calls 17)should return your answer from part b. -
You should only use Racket language features you used in PS2 or learned in the lectures on Racket expressions and declarations and Racket functions
-
Do not attempt to modify the definition of
fso that it counts the number of timesfis called by changing the contents of a global variable. -
Instead, write a new recursive function
num-f-callsthat is very much likef, but rather than returning the number calculated byfinstead returns the number of calls tofmade in that calculation.
-
-
(5 points) Define a recursive Racket function named
max-depth-fthat takes a single integer argumentnand returns the maximum stack depth (measured in terms of maximum number of nested+operations) in the evaluation of(f n). Notes:-
Add the
max-depth-ffunction to youryourAccountName-ps3-solo-functions.rktfile. -
(max-depth-f 17)should return your answer from part c. -
You should only use Racket language features you used in PS2 or learned in the lectures on Racket expressions and declarations and Racket functions
-
The
maxfunction is especially useful here. -
Do not attempt to modify the definition of
fso that it determines the stack depth by changing the contents of a global variable. -
Instead, write a new recursive function
max-depth-fthat is very much likef, but rather than returning the number calculated byfinstead returns the maximum stack depth in that calculation.
-
2. Box-and-pointer diagrams (10 points)
Consider the following box-and-pointer diagram for the list structure named a:
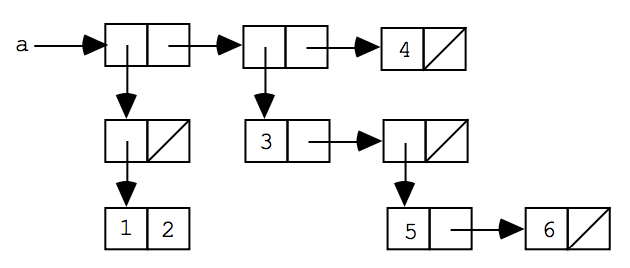
-
For each of the numbers 1 through 6, write a Racket expression that uses
carandcdrto extract that number froma. -
Write down the printed representation for a (i.e., what would be returned by the Racket interpreter for evaluating
a?). -
Write a Racket definition of the form
(define aexpr), where expr is an expression usingcons,list,
and the numbers 1 through 6 (but noquoteor quotation) to create the structure depicted in the diagram. (Once you have definedain this way, you may test your expressions from part (a).)
3. Recursive Racket List Functions (70 points)
In PS2, you wrote some recursive Racket functions that manipulate numbers. Here, you will continue to practice defining recursive Racket functions, but now you focus on functions that manipulate Racket lists. Unlike list and array data structures in many other languages, which are most naturally processed with loops, the linked-list recursively-defined nature of Racket lists make them natural candidates for recursive processing.
For each of the following Racket function specifications, write and test a recursive function that satisfies that specification. In all of your definitions, you should use the following recursive problem solving strategy:
-
For which argument(s) is the function so simple that the answer can be returned immediately? This is the base case.
-
For the other case(s) (known as the recursive case(s)), use divide/conquer/glue:
-
divide: make one or more subproblems that are smaller instances of the given problem;
-
conquer: assume that the recursive function you’re defining simply works and returns the correct answer on all of the smaller problems.
-
glue: combine the result(s) of the recursive function call(s) with information in the original problem to create the correct result for the whole problem.
-
Notes:
-
For this problem, you should use Dr. Racket to create a single file named
yourAccountName-ps3-list-functions.rktthat contains all the functions (including helper functions) that you define for this problem. -
In your definitions, unless otherwise instructed, you should not introduce any recursive helper functions. (But you can define nonrecursive helper functions).
-
If the following error message pops up during the testing of one of your functions, it mostly likely means that you have an infinite recursion that doesn’t reach its base case and runs out of memory due to a stack depth that cannot fit into available memory.
-
(5 points) Define a function
map-remainderthat takes two arguments (an integerdivisorand a listintsof integers) and returns an integer list the same length asintsin which every element is remainder of dividing the corresponding element ofintsbydivisor.> (map-remainder 2 (list 16 23 42 57 64 100)) '(0 1 0 1 0 0) > (map-remainder 3 (list 16 23 42 57 64 100)) '(1 2 0 0 1 1) > (map-remainder 5 (list 16 23 42 57 64 100)) '(1 3 2 2 4 0) > (map-remainder 17 (list 16 23 42 57 64 100)) '(16 6 8 6 13 15) -
(5 points) Define a function
filter-divisible-bythat takes two arguments (an integerdivisorand a listintsof integers) and returns a new integer list containing all the elements ofintsthat are divisible bydivisor. Usedivisible-by?from above to determine divisibility.> (filter-divisible-by 2 (list 16 23 42 57 64 100)) '(16 42 64 100) > (filter-divisible-by 3 (list 16 23 42 57 64 100)) '(42 57) > (filter-divisible-by 4 (list 16 23 42 57 64 100)) '(16 64 100) > (filter-divisible-by 5 (list 16 23 42 57 64 100)) '(100) > (filter-divisible-by 17 (list 16 23 42 57 64 100)) '() -
(5 points) Define a function
contains-multiple?that takes an integermand a list of integersnsthat returns#tifmevenly divides at least one element of the integer listns; otherwise it returns#f. Usedivisible-by?from above to determine divisibility.> (contains-multiple? 5 (list 8 10 14)) #t > (contains-multiple? 3 (list 8 10 14)) #f > (contains-multiple? 5 null) #f -
(5 points) Write a function
all-contain-multiple?that takes an integernand a list of lists of integersnss(pronounced “enziz”) and returns#tif each list of integers innsscontains at least one integer that is a multiple ofn; otherwise it returns#f. Usecontains-multiple?in your definition ofall-contain-multiple?.> (all-contain-multiple? 5 (list (list 17 10 2) (list 25) (list 3 8 5))) #t > (all-contain-multiple? 2 (list (list 17 10 2) (list 25) (list 3 8 5))) #f > (all-contain-multiple? 3 null) #t ; said to be "vacuously true"; there is no counterexample! -
(5 points) Define a function
map-consthat takes any valuexand an n-element listysand returns an n-element list of all pairs'(x . y)whereyranges over the elements ofys. The pair'(x . y)should have the same relative position in the resulting list asyhas inys.> (map-cons 17 (list 8 5 42 23)) '((17 . 8) (17 . 5) (17 . 42) (17 . 23)) > (map-cons 3 (list (list 1 6 2) (list 4 5) (list) (list 9 6 8 7))) '((3 1 6 2) (3 4 5) (3) (3 9 6 8 7)) > (map-cons 42 null) '() -
(10 points) Define a function
my-cartesian-productthat takes two listsxsandysand returns a list of all pairs'(x . y)wherexranges over the elements ofxsandyranges over the elements ofys. The pairs should be sorted first by thexentry (relative to the order inxs) and then by theyentry (relative to the order inys).> (my-cartesian-product (list 1 2) (list "a" "b" "c")) ; yes, Racket has string values '((1 . "a") (1 . "b") (1 . "c") (2 . "a") (2 . "b") (2 . "c")) > (my-cartesian-product (list 2 1) (list "a" "b" "c")) '((2 . "a") (2 . "b") (2 . "c") (1 . "a") (1 . "b") (1 . "c")) > (my-cartesian-product (list "c" "b" "a") (list 2 1)) '(("c" . 2) ("c" . 1) ("b" . 2) ("b" . 1) ("a" . 2) ("a" . 1)) > (my-cartesian-product (list "a" "b") (list 2 1)) '(("a" . 2) ("a" . 1) ("b" . 2) ("b" . 1)) > (my-cartesian-product (list 1) (list "a")) '((1 . "a")) > (my-cartesian-product null (list "a" "b" "c")) '()Notes:
- We ask you to name your function
my-cartesian-productbecause Racket already provides a similar (but slightly different)cartesian-productfunction (which you cannot use, of course). - Use the
map-consfunction from above as a helper function in yourcartesian-productdefinition. - Racket’s
appendfunction is helpful here.
- We ask you to name your function
-
(10 points) Assume that the elements of a list are indexed starting with 0. Define a function
altsthat takes a listxsand returns a two-element list of lists, the first of which has all the even-indexed elements (in the same relative order as inxs) and the second of which has all the odd-indexed elements (in the same relative order as inxs).> (alts (list 7 5 4 6 9 2 8 3)) '((7 4 9 8) (5 6 2 3)) > (alts (list 5 4 6 9 2 8 3)) '((5 6 2 3) (4 9 8)) > (alts (list 4 6 9 2 8 3)) '((4 9 8) (6 2 3)) > (alts (list 3)) '((3) ()) > (alts null) '(() ())Notes:
-
An earlier version of this problem mentioned using Racket’s
foldrfunction to solve it. That was a bug in the problem description! Do not usefoldrto definealtsin PS3; instead use regular list recursion based on the divide/conquer/glue strategy. (You will usefoldrto definealtsin PS4.). -
There is no need to treat even-length and odd-length cases differently, nor is there any need to treat the singleton list specially.
-
Racket’s
letconstruct for declaring local names is helpful for avoiding unnecessarily recalculating the recursive call.
-
-
(10 points) Define a function
insertsthat takes a valuexand an n-element listysand returns an n+1-element list of lists showing all ways to insert a single copy ofxintoys.> (inserts 3 (list 5 7 1)) '((3 5 7 1) (5 3 7 1) (5 7 3 1) (5 7 1 3)) > (inserts 3 (list 7 1)) '((3 7 1) (7 3 1) ( 7 1 3)) > (inserts 3 (list 1)) '((3 1) (1 3)) > (inserts 3 null) '((3)) > (inserts 3 (list 5 3 1)) '((3 5 3 1) (5 3 3 1) (5 3 3 1) (5 3 1 3))Notes:
- The
map-consfunction from above is useful here. - Think very carefully about the base case and the combination function for the recursive case.
- The
-
(15 points) Define a function
my-permutationsthat takes as its single argument a listxsof distinct elements (i.e., no duplicates) and returns a list of all the permutations of the elements ofxs. The order of the permutations does not matter.> (my-permutations null) '(()) > (my-permutations (list 4)) '((4)) > (my-permutations (list 3 4)) '((3 4) (4 3)) ; order doesn't matter > (my-permutations (list 2 3 4)) '((2 3 4) (3 2 4) (3 4 2) (2 4 3) (4 2 3) (4 3 2)) > (my-permutations (list 1 2 3 4)) '((1 2 3 4) (2 1 3 4) (2 3 1 4) (2 3 4 1) (1 3 2 4) (3 1 2 4) (3 2 1 4) (3 2 4 1) (1 3 4 2) (3 1 4 2) (3 4 1 2) (3 4 2 1) (1 2 4 3) (2 1 4 3) (2 4 1 3) (2 4 3 1) (1 4 2 3) (4 1 2 3) (4 2 1 3) (4 2 3 1) (1 4 3 2) (4 1 3 2) (4 3 1 2) (4 3 2 1))Notes:
- We ask you to name your function
my-permutationsbecause Racket already provides the same function namedpermutations(which you cannot use, of course). - In this problem, you are allowed to use one or more recursive helper functions.
- Although the specification allows the permuted elements to be listed in any order, the above examples show an order that works particularly well with the divide/conquer/glue strategy. In particular, study the above examples carefully to understand (1) the recursive nature of
my-permutationsand (2) why theinsertsfunction from above is helpful to use when definingmy-permutations. - In the example
(my-permutations (list 1 2 3 4)), the 24 results would normally be printed by Racket in 24 separate lines, but here they have been formatted to strongly sugggest a particular solution strategy.
- We ask you to name your function
Extra Credit: Permutations in the Presence of Duplicates (15 points)
This problem is optional. You should only attempt it after completing all the other problems.
Define a version of the my-permutations function named my-permutations-dup that correctly handles lists with duplicate elements. That is, each permutation of such a list should only be listed once in the result. You should not generate duplicate permutations and then remove them; rather, you should just not generate any duplicates to begin with. As before, the order of the permutations does not matter.
> (my-permutations-dup (list 2 1 2))
'((1 2 2) (2 1 2) (2 2 1)) ; order doesn't matter
> (my-permutations-dup (list 1 2 1 2 2))
'((1 1 2 2 2) (1 2 1 2 2) (1 2 2 1 2) (1 2 2 2 1)
(2 1 1 2 2) (2 1 2 1 2) (2 1 2 2 1)
(2 2 1 1 2) (2 2 1 2 1) (2 2 2 1 1)) ; order doesn't matter