PS2: Racket Recursion
- Due: 5pm Saturday 13 February. (The pset is due on Saturday rather than Friday because I’ve posted is late. But you should try to complete as much of it as possible before 5pm Fri 12 Februrary, while help is easily available.)
- Notes:
- This is a long assignment. Start soon!
- You should be able to do Problems 1, 2, 4a, and 4b now.
- You will be able to do all the problems after the Tue. Feb 9 class.
- The problems needn’t be done in order. Feel free to jump around.
- The problem set is worth 120 points.
- This is a long assignment. Start soon!
- Submission:
- In the yourFullName CS251 Spring 2016 Folder that you created for PS1, create a Google Doc named yourFullName CS251 PS2.
- For Problems 1 through 3, include all answers in your PS2 google doc. Please format your evaluation derivations so that they’re easy to read. Format the derivation using the fixed-width Courier New font (can use a small font size if that helps).
- For Problem 4 (Recursive Racket Functions):
- Copy the contents of
yourAccountName-ps2-functions.rktto the Google Doc. Format the definitions using the fixed-width Courier New font (can use a small font size if that helps). - Drop a copy of your
yourAccountName-ps2-functions.rktin your~/cs251/drop/ps02drop folder on cs.wellesley.edu.
- Copy the contents of
1. Truthiness (10 points)
 )
)
In the context of a conditional test, a value that chooses the then arm of the conditional is called truthy and a value that chooses the else arm of the conditional is called falsey (sometimes spelled falsy). We will use the term neither to refer to a value that cannot be used as a conditional test (causing a compile-time or run-time error).
We have seen that in Racket, the #f value is falsey and every value that is not #f is truthy; Racket has no neither values. This problem asks you to explore truthiness in other languages.
Below are four programming languages and links to their language specification documents. Based on information in the documents, determine which values are truthy, which are falsey, and which (if any) are neither. In your answers, cite the section(s) of the reference manuals that you used to determine your answer.
-
JavaScript (a.k.a. EcmaScript): http://www.ecma-international.org/publications/files/ECMA-ST/Ecma-262.pdf
-
C: http://www.open-std.org/JTC1/SC22/WG14/www/docs/n1570.pdf
Notes:
-
Hint: begin by searching for the terms if statement or conditional in the documents.
-
One of the purposes of this problem is to introduce you to language specification documents. These are the authoritative sources for answering any questions about the languages, even nit-picky ones. Although they can be somewhat dense, you should get into the habit of consulting them.
2. Sum Fun (30 points)
In class, we defined the following recursive factorial function:
(define fact
(lambda (n)
(if (= n 0)
1
(* n (fact (- n 1))))))We can use the small-step semantics introduced in lecture on Fri. Feb 5 to explain the evaluation of (fact 4). To simplify things, let’s introduce the abbreviation λ_fact for the lambda expression
(lambda (n) (if (= n 0) 1 (* n (fact (- n 1)))))Then here is the small-step evaluation derivation for (fact 4):
(fact 4)
⇒ (λ_fact 4)
⇒ (if (= 4 0) 1 (* 4 (fact (- 4 1))))
⇒ (if #f 1 (* 4 (fact (- 4 1))))
⇒ (* 4 (fact (- 4 1)))
⇒ (* 4 (λ_fact (- 4 1)))
⇒ (* 4 (λ_fact 3))
⇒ (* 4 (if (= 3 0) 1 (* 3 (fact (- 3 1)))))
⇒ (* 4 (if #f 1 (* 3 (fact (- 3 1)))))
⇒ (* 4 (* 3 (fact (- 3 1))))
⇒ (* 4 (* 3 (λ_fact (- 3 1))))
⇒ (* 4 (* 3 (λ_fact 2)))
⇒ (* 4 (* 3 (if (= 2 0) 1 (* 2 (fact (- 2 1))))))
⇒ (* 4 (* 3 (if #f 1 (* 2 (fact (- 2 1))))))
⇒ (* 4 (* 3 (* 2 (fact (- 2 1)))))
⇒ (* 4 (* 3 (* 2 (λ_fact (- 2 1)))))
⇒ (* 4 (* 3 (* 2 (λ_fact 1))))
⇒ (* 4 (* 3 (* 2 (if (= 1 0) 1 (* 1 (fact (- 1 1)))))))
⇒ (* 4 (* 3 (* 2 (if #f 1 (* 1 (fact (- 1 1)))))))
⇒ (* 4 (* 3 (* 2 (* 1 (fact (- 1 1))))))
⇒ (* 4 (* 3 (* 2 (* 1 (λ_fact (- 1 1))))))
⇒ (* 4 (* 3 (* 2 (* 1 (λ_fact 0)))))
⇒ (* 4 (* 3 (* 2 (* 1 (if (= 0 0) 1 (* 0 (fact (- 0 1))))))))
⇒ (* 4 (* 3 (* 2 (* 1 (if #t 1 (* 0 (fact (- 0 1))))))))
⇒ (* 4 (* 3 (* 2 (* 1 1))))
⇒ (* 4 (* 3 (* 2 1)))
⇒ (* 4 (* 3 2))
⇒ (* 4 6)
⇒ 24To highlight the essential steps of such an evaluation, we will often use the notation e1 ⇒* e2 to mean that expression e1 rewrites to expression e2 by some number (possibly zero) of ⇒ steps, and then omit all lines except for the ones involving (1) calls to λ_fact on argument values or (2) calculation of the final result. Here’s an example of an abbreviated evaluation derivation for the above example:
(λ_fact 4)
⇒* (* 4 (λ_fact 3))
⇒* (* 4 (* 3 (λ_fact 2)))
⇒* (* 4 (* 3 (* 2 (λ_fact 1))))
⇒* (* 4 (* 3 (* 2 (* 1 (λ_fact 0)))))
⇒* (* 4 (* 3 (* 2 (* 1 1))))
⇒ (* 4 (* 3 (* 2 1)))
⇒ (* 4 (* 3 2))
⇒ (* 4 6)
⇒ 24As another example, consider a recursive definition of a function for calculating the nth Fibonacci number:
(define fib
(lambda (n)
(if (<= n 1)
n
(+ (fib (- n 1)) (fib (- n 2))))))Suppose λ_fib is an abbreviation for the lambda expression
(lambda (n)
(if (<= n 1)
n
(+ (fib (- n 1)) (fib (- n 2))))))Then here is an abbreviated evaluation derivation for (fib 4)
(λ_fib 4)
⇒* (+ (λ_fib 3) (fib (- 4 2)))
⇒* (+ (+ (λ_fib 2) (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ (+ (λ_fib 1) (fib (- 2 2))) (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ (+ 1 (λ_fib 0)) (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ (+ 1 0) (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ 1 (λ_fib 1)) (fib (- 4 2)))
⇒* (+ (+ 1 1) (fib (- 4 2)))
⇒* (+ 2 (λ_fib 2))
⇒* (+ 2 (+ (λ_fib 1) (fib (- 2 2))))
⇒* (+ 2 (+ 1 (λ_fib 0)))
⇒* (+ 2 (+ 1 0))
⇒ (+ 2 1)
⇒ 3Note that (λ_fib 4) ⇒* (+ (λ_fib 3) (fib (- 4 2))) and not (λ_fib 4) ⇒* (+ (λ_fib 3) (λ_fib 2)). Why? Because the small-step evaluation of (+ e1 e2) must fully evaluate e1 to a value v1 before any evaluation is performed on e2. So the expression (fib (- 4 2)) is not simplified in any way until (λ_fib 3) evaluates to 2.
In this problem you are asked to reason about and create such abbreviated derivations.
a. Alternative if semantics (2 points)
The small-step reduction rules for if expressions in Racket are
(if v_test e_then e_else) ⇒ e_then, ifv_testis a value that is not#f(if nonfalse)(if #f e_then e_else) ⇒ e_else(if false)
Lois Reasoner thinks that the reduction of if expressions should be changed to:
(if v_test v_then v_else) ⇒ v_then, ifv_testis a value that is not#f(if nonfalse Lois)(if #f v_then v_else) ⇒ v_else(if false Lois)
These differ from the actual rules by requiring that all three subexpressions e_test, e_then, and e_false of (if e_test e_then e_false) are first evaluated to values before the if expression can be simplified.
Explain that Lois’s alternative semantics for if are a bad idea. For example, what would happen in the evaluation of (fact 4) if Lois’s rules were used?
b. sum-between (4 points)
Here is a definition of a sum-between function that returns the sum of all the integers between its two integer arguments (inclusive):
(define sum-between
(lambda (lo hi)
(if (> lo hi)
0
(+ lo (sum-between (+ lo 1) hi)))))Using the abbreviated small-step derivation notation shown above for (fact 4), show an abbreviated evaluation derivation for (sum-between 3 7) that shows the key steps in this derivation. Use the notation λ_sb as an abbreviation for the lambda expression
(lambda (lo hi)
(if (> lo hi)
0
(+ lo (sum-between (+ lo 1) hi))))Your derivation should only show lines in which λ_sb is called on values and lines involving the calculation of + in (+ lo ..., but not any lines that involve if, >, or the calculation of + in (+ lo 1).
c. Stack depth for sum-between (3 points)
Although the small-step evaluation model does not have any explicit notion of stack frames, operations like * in the recursive fact definition and + in the recursive sum-between definition correspond to pending operations that are remembered to be performed when control returns the stack frame for a particular function invocation in a model based on stack frames. In the (fact 4) example, the fact that the maximal sequence of nested multiplications, (* 4 (* 3 (* 2 (* 1 1)))), has five multiplications corresponds to a nesting of five stack frames (one for each call of fact on arguments 4 down to 0).
In the case of fact, we will call the maximal number of pending multiplications the stack depth. So (fact 4) has a stack depth of 4, and (fact 100) would have a stack depth of 100. So the stack depth of (fact n) grows linearly in n.
Let’s define the stack depth for sum-between to be the maximal number of nested pending addition operations in the small-step evaluation derivation.
-
What is the stack depth for
(sum-between 3 7)? -
What is the stack depth for
(sum-between 1 128)? -
How does the stack depth for
(sum-between 1 n)grow withn?
d. sum-between-halves (10 points)
Here is a definition of a sum-between-halves function that also returns the sum of all the integers between its two integer arguments (inclusive), but does so in a different way from sum-between:
(define sum-between-halves
(lambda (lo hi)
(if (> lo hi)
0
(if (= lo hi)
lo
(+ (sum-between-halves lo (quotient (+ lo hi) 2))
(sum-between-halves (+ 1 (quotient (+ lo hi) 2)) hi))))))Show an abbreviated evaluation derivation for (sum-between-halves 3 7) that shows the key steps in this derivation. Use the notation λ_sbh as an abbreviation for the lambda expression
(lambda (lo hi)
(if (> lo hi)
0
(if (= lo hi)
lo
(+ (sum-between-halves lo (quotient (+ lo hi) 2))
(sum-between-halves (+ 1 (quotient (+ lo hi) 2)) hi))))))Your derivation should be similar to the (fib 4) example given above. Note that somes lines will have a mixture of calls to λ_sbh on values and calls to sum-between-halves on unevaluated expressions. See the (fib 4) example for an explanation of this. For example, your derivation should begin like this:
(λ_sbh 3 7)
⇒* (+ (λ_sbh 3 5)
(sum-between-halves (+ 1 (quotient (+ 3 7) 2)) 7))
⇒* (+ (+ (λ_sbh 3 4)
(sum-between-halves (+ 1 (quotient (+ 3 5) 2)) 5))
(sum-between-halves (+ 1 (quotient (+ 3 7) 2)) 7))e. Stack depth for sum-between-halves (5 points)
Define the stack depth for a call to sum-between-halves as the maximal number of nested pending + operations from (+ (sum-between-halves ...) (sum-between-halves ...)).
-
What is the stack depth for
(sum-between-halves 3 7)? -
What is the stack depth for
(sum-between 1 128)? -
How does the stack depth for
(sum-between-halves 1 n)grow withn? -
Does
sum-between-halvesoffer any benefit oversum-betweenas a way to calculate the sum of integers in a range?
f. sum-between-iter (4 points)
Now we consider one more way to calculate the sum of integers in a given range. The function sum-between-iter defined below also sums numbers in a given range using the helper function sum-between-tail.
(define sum-between-iter
(lambda (lo hi)
(sum-between-tail lo hi 0)))
(define sum-between-tail
(lambda (lo hi sum-so-far)
(if (> lo hi)
sum-so-far
(sum-between-tail (+ lo 1) hi (+ lo sum-so-far)))))Show an abbreviated evaluation derivation for (sum-between-iter 3 7) that shows the key steps in this derivation. Use the notation λ_sbi as an abbreviation for the lambda expression
(lambda (lo hi)
(sum-between-tail lo hi 0)))and the notation λ_sbt as an abbreviation for the lambda expression
(lambda (lo hi sum-so-far)
(if (> lo hi)
sum-so-far
(sum-between-tail (+ lo 1) hi (+ lo sum-so-far)))))In your derivation, show only lines in which λ_sbi or λ_sbt are called on values.
g. Benefits of sum-between-iter/sum-between-tail (2 points)
Do sum-between-iter/sum-between-tail offer any benefit(s) over sum-between and sum-between-halves? Explain.
3. Box-and-pointer diagrams (10 points)
Consider the following box-and-pointer diagram for the list structure named a:
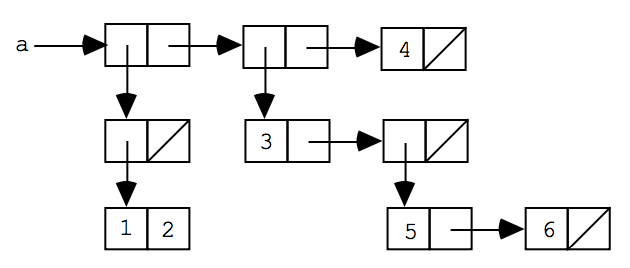
-
For each of the numbers 1 through 6, write a Racket expression that uses
carandcdrto extract that number froma. -
Write down the printed representation for a (i.e., what would be returned by the Racket interpreter for evaluating
a?). -
Write a Racket definition of the form
(define aexpr), where expr is an expression usingcons,list,
and the numbers 1 through 6 (but noquoteor quotation) to create the structure depicted in the diagram. (Once you have definedain this way, you may test your expressions from part (a).)
4. Recursive Racket functions (70 points)
Although you’ve written recursive function definitions before in other courses, recursion is particularly important in CS251 for three reasons:
-
The list data structures in Racket and Standard ML are recursively defined, and so are naturally processed with recursion.
-
Neither Racket nor Standard ML has looping constructs, so what you would express via loops in other languages must be expressed via recursion in these languages. (We’ll see that a particular kind of recursion known as tail recursion can express anything expressible with loops in other languages and then some.)
-
Later in the semester we will study metaprograms – i.s., programs that manipulate other programs. Metaprograms typically process the abstract syntax tree (AST) structure of the program being manipulated. Such tree processing is most naturally expressed using recursion. Indeed, you’ve already seen that big-step evaluation semantics is recursive in nature.
For each of the following Racket function specifications, write and test a recursive function that satisfies that specification. In all of your definitions, you should use the following recursive problem solving strategy:
-
For which argument(s) is the function so simple that the answer can be returned immediately? This is the base case.
-
For the other case(s) (known as the recursive case(s)), use divide/conquer/glue:
-
divide: make one or more subproblems that are smaller instances of the given problem;
-
conquer: assume that the recursive function you’re defining simply works and returns the correct answer on all of the smaller problems.
-
glue: combine the result(s) of the recursive function call(s) with information in the original problem to create the correct result for the whole problem.
-
The fact, fib, sum-between and sum-between-halves functions shown above are all instances of this strategy, and we will see many examples of recursion with list arguments in the coming week. (The sum-between-iter function is not an instance of this strategy because it introduces a helper function that changes the structure of the problem into an iteration.)
Notes:
-
For this problem, you should use Dr. Racket to create a single file named
yourAccountName-ps2-functions.rktthat contains all the functions (including helper functions) that you define for this problem. -
In your definitions, unless otherwise instructed, you should not introduce any recursive helper functions. (But you can define nonrecursive helper functions).
-
If the following error message pops up during the testing of one of your functions, it mostly likely means that you have an infinite recursion that doesn’t reach its base case and runs out of memory due to a stack depth that cannot fit into available memory.
-
(7 points) Define a function
sum-squares-of-ints-divisible-bythat takes three integer arguments (divisor,lo, andhi) and returns the sum of the squares of all the integers betweenloandhi(inclusive) that are evenly divisible bydivisor.> (sum-squares-of-ints-divisible-by 2 1 8) 120 ; = 2^2 + 4^2 + 6^2 + 64^2 > (sum-squares-of-ints-divisible-by 3 1 10) 126 ; = 3^2 + 6^2 + 9^2 > (sum-squares-of-ints-divisible-by 5 1 10) 125 ; = 5^2 + 10^2 > (sum-squares-of-ints-divisible-by 7 1 10) 49 ; = 7^2 > (sum-squares-of-ints-divisible-by 11 1 10) 0 ; no multiples of 11 between 1 and 10 > (sum-squares-of-ints-divisible-by 11 7 15) 121 ; = 11^2 > (sum-squares-of-ints-divisible-by 2 10 8) 0 ; the range "from 10 up to 8" is emptyUse the following helper function, which is helpful in this problem and some of the following ones.
(define divisible-by? (lambda (num divisor) (= (remainder num divisor) 0))) -
(8 points) A Hamming number is any positive integer expressible as 2i⋅3j⋅5k. E.g., the Hamming numbers between 1 and 100 are:
1 2 3 4 5 6 8 9 10 12 15 16 18 20 24 25 27 30 32 36 40 45 48 50 54 60 64 72 75 80 81 90 96 100Define a function
hamming?that takes a single numeric argument (including 0, negatives, and nonintegers), and returns#tif the argument is a Hamming number and#fif it is not. Your function need not work on arguments that are not numbers.> (hamming? 30) #t > (hamming? 31) #f > (hamming? -31) #f > (hamming? 3.141) #f > (hamming? 0) #f > (filter hamming? (range -100 101)) ; list all integers from -100 up to (but not including 101) ; for which hamming? is true '(1 2 3 4 5 6 8 9 10 12 15 16 18 20 24 25 27 30 32 36 40 45 48 50 54 60 64 72 75 80 81 90 96 100)Notes:
- Use
integer?to test if a value is an integer. - Use
(and e1 e2 ... en)to determine if all of the expressionse1,e2, …,enare true. - Use
(or e1 e2 ... en)to determine if at least one the expressionse1,e2, …,enis true. - You needn’t use any
ifexpressions in your definition. All you need areandandor. (But you can useifif you want to.) - The
divisible-by?helper function from above is useful.
- Use
-
(5 points) Define a function
filter-divisible-bythat takes two arguments (an integerdivisorand a listintsof integers) and returns a new integer list containing all the elements ofintsthat are divisible bydivisor. Usedivisible-by?from above to determine divisibility.> (filter-divisible-by 2 (list 16 23 42 57 64 100)) '(16 42 64 100) > (filter-divisible-by 3 (list 16 23 42 57 64 100)) '(42 57) > (filter-divisible-by 4 (list 16 23 42 57 64 100)) '(16 64 100) > (filter-divisible-by 5 (list 16 23 42 57 64 100)) '(100) > (filter-divisible-by 17 (list 16 23 42 57 64 100)) '() -
(5 points) Define a function
contains-multiple?that takes an integermand a list of integersnsthat returns#tifmevenly divides at least one element of the integer listns; otherwise it returns#f. Usedivisible-by?from above to determine divisibility.> (contains-multiple? 5 (list 8 10 14)) #t > (contains-multiple? 3 (list 8 10 14)) #f > (contains-multiple? 5 null) #f -
(5 points) Write a function
all-contain-multiple?that takes an integernand a list of lists of integersnss(pronounced “enziz”) and returns#tif each list of integers innsscontains at least one integer that is a multiple ofn; otherwise it returns#f. Usecontains-multiple?in your definitiofall-contain-multiple?.> (all-contain-multiple? 5 (list (list 17 10 2) (list 25) (list 3 8 5))) #t > (all-contain-multiple? 2 (list (list 17 10 2) (list 25) (list 3 8 5))) #f > (all-contain-multiple? 3 null) #t ; said to be "vacuously true"; there is no counterexample! -
(5 points) Define a function
map-consthat takes any valuexand an n-element listysand returns an n-element list of all pairs'(x . y)whereyranges over the elements ofys. The pair'(x . y)should have the same relative position in the resulting list asyhas inys.> (map-cons 17 (list 8 5 42 23)) '((17 . 8) (17 . 5) (17 . 42) (17 . 23)) > (map-cons 3 (list (list 1 6 2) (list 4 5) (list) (list 9 6 8 7))) '((3 1 6 2) (3 4 5) (3) (3 9 6 8 7)) > (map-cons 42 null) '() -
(10 points) Define a function
my-cartesian-productthat takes two listsxsandysand returns a list of all pairs'(x . y)wherexranges over the elements ofxsandyranges over the elements ofys. The pairs should be sorted first by thexentry (relative to the order inxs) and then by theyentry (relative to the order inys).> (my-cartesian-product (list 1 2) (list "a" "b" "c")) ; yes, Racket has string values '((1 . "a") (1 . "b") (1 . "c") (2 . "a") (2 . "b") (2 . "c")) > (my-cartesian-product (list 2 1) (list "a" "b" "c")) '((2 . "a") (2 . "b") (2 . "c") (1 . "a") (1 . "b") (1 . "c")) > (my-cartesian-product (list "c" "b" "a") (list 2 1)) '(("c" . 2) ("c" . 1) ("b" . 2) ("b" . 1) ("a" . 2) ("a" . 1)) > (my-cartesian-product (list "a" "b") (list 2 1)) '(("a" . 2) ("a" . 1) ("b" . 2) ("b" . 1)) > (my-cartesian-product (list 1) (list "a")) '((1 . "a")) > (my-cartesian-product null (list "a" "b" "c")) '()Notes:
- We ask you to name your function
my-cartesian-productbecause Racket already provides a similar (but slightly different)cartesian-productfunction (which you cannot use, of course). - Use the
map-consfunction from above as a helper function in yourcartesian-productdefinition. - Racket’s
appendfunction is helpful here.
- We ask you to name your function
-
(10 points) Define a function
insertsthat takes a valuexand an n-element listysand returns an n+1-element list of lists showing all ways to insert a single copy ofxintoys.> (inserts 3 (list 5 7 1)) '((3 5 7 1) (5 3 7 1) (5 7 3 1) (5 7 1 3)) > (inserts 3 (list 7 1)) '((3 7 1) (7 3 1) ( 7 1 3)) > (inserts 3 (list 1)) '((3 1) (1 3)) > (inserts 3 null) '((3)) > (inserts 3 (list 5 3 1)) '((3 5 3 1) (5 3 3 1) (5 3 3 1) (5 3 1 3))Notes:
- The
map-consfunction from above is useful here. - Think very carefully about the base case and the combination function for the recursive case.
- The
-
(15 points) Define a function
my-permutationsthat takes as its single argument a listxsof distinct elements (i.e., no duplicates) and returns a list of all the permutations of the elements ofxs. The order of the permutations does not matter.> (my-permutations null) '(()) > (my-permutations (list 4)) '((4)) > (my-permutations (list 3 4)) '((3 4) (4 3)) ; order doesn't matter > (my-permutations (list 2 3 4)) '((2 3 4) (3 2 4) (3 4 2) (2 4 3) (4 2 3) (4 3 2)) > (my-permutations (list 1 2 3 4)) '((1 2 3 4) (2 1 3 4) (2 3 1 4) (2 3 4 1) (1 3 2 4) (3 1 2 4) (3 2 1 4) (3 2 4 1) (1 3 4 2) (3 1 4 2) (3 4 1 2) (3 4 2 1) (1 2 4 3) (2 1 4 3) (2 4 1 3) (2 4 3 1) (1 4 2 3) (4 1 2 3) (4 2 1 3) (4 2 3 1) (1 4 3 2) (4 1 3 2) (4 3 1 2) (4 3 2 1))Notes:
- We ask you to name your function
my-permutationsbecause Racket already provides the same function namedpermutations(which you cannot use, of course). - In this problem, you are allowed to use one or more recursive helper functions.
- Although the specification allows the permuted elements to be listed in any order, the above examples show an order that works particularly well with the divide/conquer/glue strategy. In particular, study the above examples carefully to understand (1) the recursive nature of
my-permutationsand (2) why theinsertsfunction from above is helpful to use when definingmy-permutations. - In the example
(my-permutations (list 1 2 3 4)), the 24 results would normally be printed by Racket in 24 separate lines, but here they have been formatted to strongly sugggest a particular solution strategy.
- We ask you to name your function
Extra Credit: Permutations in the Presence of Duplicates (15 points)
This problem is optional. You should only attempt it after completing all the other problems.
Define a version of the my-permutations function named my-permutations-dup that correctly handles lists with duplicate elements. That is, each permutation of such a list should only be listed once in the result. You should not generate duplicate permutations and then remove them; rather, you should just not generate any duplicates to begin with. As before, the order of the permutations does not matter.
> (my-permutations-dup (list 2 1 2))
'((1 2 2) (2 1 2) (2 2 1)) ; order doesn't matter
> (my-permutations-dup (list 1 2 1 2 2))
'((1 1 2 2 2) (1 2 1 2 2) (1 2 2 1 2) (1 2 2 2 1)
(2 1 1 2 2) (2 1 2 1 2) (2 1 2 2 1)
(2 2 1 1 2) (2 2 1 2 1) (2 2 2 1 1)) ; order doesn't matter