CS307: Reading on Color

Color Models

Several color models are common in CG. We'll go over all of these in the second half of this reading; for this half, we'll focus on RGB.

Color Vision

Our retinas happen to have rod-shaped cells that are sensitive to all light, and cone-shaped cells that come in three kinds: red-sensitive, green-sensitive, and blue-sensitive. Therefore, there are three (additive) primary colors: Red, Green and Blue or RGB. All visible colors are seen by exciting these three types of cells in various degrees. (Take a look at the Wikipedia page on Trichromacy for a good introduction.) The consequence is that almost any color can be mimicked by some amount of Red, some amount of Green, and some amount of Blue.

Color monitors and TV sets use RGB to display all their colors, including yellow, chartreuse, you name it. If we imagine that the amount of a primary color (Red, Green or Blue) is measured by a number from 0 to 255 inclusive, we can represent a color by a triple of numbers, such as (255,0,0), which is pure Red, and so forth. Here are some more interesting examples:

You can find more examples of these in any of zillions of color reference pages on the web.

Demo: RGB Color Cube

The RGB color system is 3-dimensional. That is, you can think of it as a cube with three perpendicular axes: Red, Green and Blue. Because of the way our eyes work, that is sufficient to capture nearly every color.

Here's an example of a color cube, built in Three.js:

A screenshot from an earlier version:

Color Cube

In the picture above, the red vertex is color (1,0,0): 1 on the red axis and zeros elsewhere. The green vertex is color (0,1,0) and the blue vertex is color (0,0,1). These are the primary colors. (Often, we normalize the RGB coordinates to [0-1]. You can think of it as a fraction of the maximum intensity. In the color cubes above, I have made the red axis the same as the x axis, the green with y, and the blue with z.)

The magenta vertex at the bottom is color (1,0,1). The cyan vertex is (0,1,1). The yellow vertex is (1,1,0). These are the secondary colors.

The white vertex in the center is color (1,1,1). The black vertex that we can see if we drag the WebGL color cube around is color (0,0,0).

Others of the millions of colors correspond to points in the interior of the cube. For example, Cornflower might be represented as:

R = 100/255 = 0.39
G = 149/255 = 0.58
B = 237/255 = 0.93

Of course, as you may know, integer division in C and in Python yields an integer result, so all the fractions in the example above evaluate to zero — hardly useful. Instead, we need to explicitly use floating point values. One way is to enter the values with decimal points.

R = 100.0/255.0 = 0.39
G = 149.0/255.0 = 0.58
B = 237.0/255.0 = 0.93

(Fortunately, integer division is not an issue with JavaScript, so you don't have to worry about it, but this trick of using decimal points is good to remember.)

Thought questions:

For more info, consult the Wikipedia article on RGB

Specifying RGB Colors in Three.js

Three.js has a Color class that allows you to enter colors in a variety of ways: 

var red1 = new THREE.Color( 0xff0000 );  // hexadecimal triple
var red3 = new THREE.Color( 1, 0, 0 );  // color cube
var red2 = new THREE.Color( "rgb(255,0,0)" );  // CSS string
var red4 = new THREE.Color( "red" ); // CSS string
alert(red1.equals(red2) && red2.equals(red3) && red3.equals(red4));
alert("Numeric value: "+red1.getHex())
alert("Hex String: "+red1.getHexString());

Demo: Red Barn

We can use that idea in this demo to make a red barn:

Here's the relevant part of the code:

As you can see, the geometry of the barn is the same, but the material is different. In this case, it's a THREE.MeshBasicMaterial that is set to a particular color. For some reason, THREE.js requires a numeric value, rather than accepting one of its own Color objects, but the Color objects have a method, getHex() which produces a numeric value that we can use. (The method name implies that the value is hex, but it's just a number, so you can print it in decimal or hex or whatever).

You'll notice that the red barn above lacks a lot of depth cues because there's no shading. Later, we'll learn about materials that interact with light to produce nice shading.

Multi-Color Barns

In principle, each face (triangle) of a Three.js geometry object can be a different color. Setting it up is a bit more complicated than what we have so far, because we need to specify a color for each face. There are essentially two parts to the change:

Note that if pretty much every face has a different color (material index), you might just decide to have the array of materials be the same length as the array of faces (possibly with some repetitions), and match them up one-to-one. If you decide to do this, you might use TW.setMaterialForFaces11, which does the following: 

  


Demo: Multi-Color Barn



Here it is in
  action: multi-colored
  barn:
  





Let's look at the code.  First, the changed geometry:







You may have to look back at the definition
  of TW.createBarn (all TW code is
  in /~cs307/threejs/libs/tw.js)
  to see how the faces were set up, or you could trust me that I got the
  indexes correct.


The code uses a TW function to set the material index of several faces
  at once.  For example, if faces 0-5 are all material m, our
  code would be tedious repetition of assignment statements like this:
  

  barnGeometry.faces[0].materialIndex = m;
  barnGeometry.faces[1].materialIndex = m;
  barnGeometry.faces[2].materialIndex = m;
  barnGeometry.faces[3].materialIndex = m;
  barnGeometry.faces[4].materialIndex = m;
  barnGeometry.faces[5].materialIndex = m;




Instead, we can say this:

    TW.setMaterialForFaces(barnGeometry, m, 0, 1, 2, 3, 4, 5);




Finally, given such a geometry, we can create a list of materials to
  apply:





Note the array that spans lines 11 - 15; square brackets could easily
  be overlooked, but the argument to THREE.MeshFaceMaterial
  is an array of materials.


As you can see, we easily apply different colors to this barn, say to
  make it all red and green at Christmas, or orange and black on
  Halloween.  However, if we wanted to make the front a different color
  from the back, we'd have to dig into the geometry object, make the
  material index for the back three faces different from the material
  index for the front three faces, and then use a five-element list of
  colors.





Coding Colors



One thing to consider is coding technique and how to name your
variables.  It seems intuitive to use a variable
like cornflower above to hold an instance
of THREE.Color() with the values for cornflower, and then
whatever you want to use that variable whenever you want something that
color, such as the sky or a barn.  But suppose that later, you want to
make the sky a bit darker or the barn green.  You could find all the
places in your program where you use the cornflower variable
and replace it with a variable name for a different color, or you
could adjust the values in the variable. But then cornflower
doesn't mean cornflower any more, which is very weird.


An alternative is to name the variable by what its purpose
or use is.  Such as:


var skyColor = new THREE.Color( 0.39, 0.58, 0.93 ); // use cornflower for the sky




Later, if you decide to change the color of the sky, you can change the
definition of skyColor and everything adjusts correctly.
This is a powerful idea.


You can even combine these approaches, by defining some of the
colors you will use and then assigning them to various uses:


var cornflower = new THREE.Color( 0.39, 0.58, 0.93 );
var skyColor = cornflower;  // use cornflower for the sky
...




Smooth and Flat Shading



There is special hardware on a graphics card for computing the color of
  a fragment (such as a triangle).  This hardware is called
  the shader, and modern OpenGL programming allows you to write
  code for the shader.  Fortunately, the THREE.js software writes these
  shaders for us.


When shading a fragment where the vertices are different colors, the
  shader has two choices:





Parametric Equation for a Line



To learn how OpenGL does this linear interpolation, we first have to
understand how OpenGL represents lines.  It uses parametric
equations.  Suppose we want to define a line from point A to point B.
(Points A and B could be in 2D or 3D; everything works the same).  All the
following are equivalent:



P(t) = A + vt

P(t) = A + (B-A)t

P(t) = A(1-t) + B*t





All of these equations generate a point on the line given the value of
the t.  The parameter t can be any real number.  Any value of t generates a
point on the line.  Thus, the 3D line is like the number line, with t=0 at
A and t=1 at B.


The first equation form, above, defines the line using point A and a
vector, v.  Thinking visually, A is a dot and v is an arrow:
point A is the starting point and vector v is the direction.  For example,
A might be "the center of Boston Common," and v might be "north" or "south
by south west."  If you start at A and go in direction v, your path will
be a line.  If we imagine that you start at A at time 0 and you move with
constant velocity, any point on the line is defined just by the time.  For
example, P(4.5) would be your location 4.5 hours after you started.


The second equation uses two points, A and B, and substitutes B-A for
the vector v.  This is because one way to define a vector is to subtract
two points.  For example, if point B is "Logan Airport," we can define a
line from point A to point B and we only implicitly know the compass
heading, but we know that we're heading directly to the airport (as the
crow flies).  Interestingly, because of the way the vector is defined, we
know we'll reach the airport exactly when t=1.  As with the first form of
the equation, any value for t generates exactly one point on the line.


The third form of the equation is just a bit of algebraic rearrangement
of the second form.  It emphasizes the idea that any point on the line
segment from A to B can be defined as a mixture of A and B in some
proportion.  The midpoint is a 50/50 mixture (a parameter value of 0.5),
but a 25/75 mixture is a point three fourths of the way towards B.  (The
greater the proportion of B, the closer we are to B.)


We can define lines that go through the same points but that have
different equations.  For example, a line from B to A.  In that case, the
equation looks like:


Q(s) = B + (A-B)s




With this line, s=0 is at B and s=1 is at A, so the line starts at B
and goes through A.  It generates the same points as P(t), but the
interpretation of the parameter is different.  In this case, the parameter
goes in the opposite direction.  (Someone driving on 95 from Boston to New
York City drives the same road as someone driving on 95 from New York City
to Boston, so it's the same line, but a different journey.)


Parametric Line Metaphor: Bug Paths





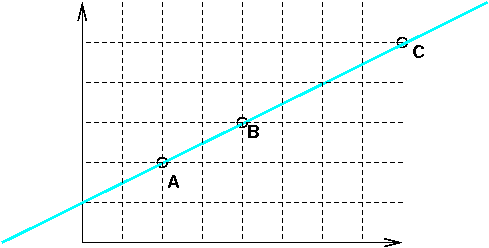
a line in a 2D coordinate system
  
Figure 1: a line in a 2D coordinate system





The math above works fine, but might be a little dry.  Let's explore
  some metaphors for parametric equations. To start with, consider the
  picture in figure 1.  The coordinates of the points are:

  



Suppose we have an ant crawling along the line.  The ant starts at
  point A at time 0 and proceeds in a determined, steady, ant-like way to
  the upper right, arriving at B at time 1. Let's measure time in minutes
  and position in meters. We can say that
  
    

    
  1. The ant is moving along the vector V=B-A=(2,1). This means it's
      moving to the right twice as fast as it's moving up: the slope of
      the line is 1/2.

    
  2. The parametric equation of the line is P(t)=A+V*t.

    
  3. The ant's height as a function of time is y(t)=2+t, because it
    starts at A at time 0, and A's height is 2, and the ant's height
    increases at 1 meter per minute.

    
  4. The ant's horizontal position as a function of time is x(t)=2+2t,
    because it starts at A at time 0 and A's x coordinate is 2, and the
    ant's x coordinate increases at 2 meters per minute.

    
  5. The points A and B differ by 2 along the x direction and by 1
    along the y direction. Their total distance is
    sqrt(22+12) or sqrt(5).

    
  6. The ant's velocity along the line is sqrt(5) meters per minute.
    Sqrt(5) is the distance between A and B, and also the length of the
    velocity vector, since the way that we defined the parametric equation
    means that, by definition, the ant takes 1 time unit to get from A to
    B. That's because P(0)=A and P(1)=B.

  



Suppose we have a different bug, maybe a beetle, that starts at B at
  time zero and gets to C at time 1.  We can make corresponding 
  observations:

  
    

    
  1. The beetle is moving along the vector W=C-B=(4,2). This means
      that, like the ant, it's moving to the right twice as fast as it's
      moving up.  The velocity vector of the beetle, W, is exactly twice
      that of the ant, V, so the beetle is moving twice as fast as the
      ant.

    
  2. The parametric equation of the line is Q(t)=B+W*t.

    
  3. The beetle's height as a function of time is y(t)=3+4t, because it
    starts at B at time 0, and B's height is 3, and the beetle's height
    increases at 2 meters per minute.

    
  4. The beetle's horizontal position as a function of time is
    x(t)=4+4t, because it starts at B at time 0 and B's x coordinate is 4,
    and the beetle's x coordinate increases at 4 meters per minute.

    
  5. The points B and C differ by 4 along the x direction and by 1
    along the y direction. Their total distance is
    sqrt(42+22) or sqrt(20).  Note that
    sqrt(20)=2*sqrt(5), which isn't too surprising, since C is twice as
    far from B as A is.

    
  6. The beetle's velocity along the line is sqrt(20) meters per
    minute.  Sqrt(20) is the length of the velocity vector and the
    distance between B and C.  Once again Q(0)=B and Q(1)=C.

  



But wait, you say. These stories of ants and beetles are all very good,
  but it's the same darn line.  Are there two different equations
  for this one line?


Yes.  One feature of parametric equations is that there are infinitely
  many equations for a particular line. We can choose one that is
  convenient for the problem we want to solve and the points we are given.
  Also, we can ask questions like:
  
Suppose a centipede starts at C at time 0 and gets to A
  at time 1.  At what time does it meet (and eat) the ant? Where does this
  gruesome event occur?




Before we answer that question, let's look at another situation, this
  with two lines:




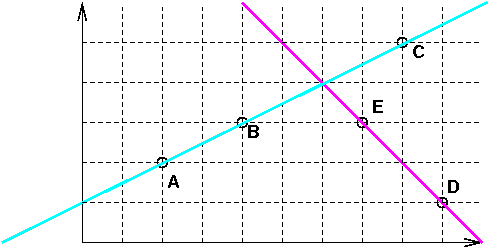
two lines in a 2D coordinate system
  
Figure 2: two lines in a 2D coordinate system





We now have two lines, the cyan one and the magenta one.  We can see
  that they intersect, but where?  Do the bugs meet?  Convince yourself of
  the following:
  



In a way, I find the parameter somewhat reassuring, because a line is,
  intuitively, a one-dimensional thing, so a single, one-dimensional
  number should be sufficient for specifying a location on the line.
  That's exactly what the parameter does: it specifies where on the line a
  point is. 


Parametric Line Metaphor: Mixtures



Forget about bugs crawling through a 2D Cartesian grid, or even flying
  through a 3D Cartesian space.  Let's think about parametric lines in a
  different say, namely as a weighted average or as
  a mixture.


To start, I'm going to repeat figure 1, now as figure 3:




a line in a 2D coordinate system
  
Figure 3: a line in a 2D coordinate system





Let's think about a line from A to C:


  P(t) = A + (C-A)t

  P(t) = A + Ct - At

  P(t) = A(1-t) + Ct




Intuitively, the point B is 1/3rd of the way from A to C, so we can
  make the following observations:
  

  

Thus, points on the line segment from A to C can be viewed as weighted
  averages of the two endpoints. For example, if a course's grade depends
  only on a midterm and a final, and the final counts twice as much as the
  midterm, you'd compute the course grade as:
  

    grade = midterm*(1/3) + final*(2/3)
  



That's exactly the kind of equation we have for this line!


We can also think of the points on the line segment as
  different mixtures of the endpoints.  For example, when cooking
  rice, we need to get the right balance of rice and water.  If the point
  A represents 100% water and the point C represents 100% rice, the
  parameter of any point on the line segments represents a ratio of rice
  to water.


The point B has a parameter of 1/3, so that means it's a mixture of 2/3
  of A (the water) and 1/3 of C (the rice).  Remember the parameter and
  the weights are inversely related: the parameter tells how far we are
  from the starting point, and the weight is proportional to how near we
  are to an endpoint.

  

  

Note that the mixture metaphor doesn't work so well for points
  on the line but outside the line segment (110% rice and -10% water?),
  but it works very well for points on the interior of the line segment,
  and computer graphics is usually more concerned with line segments than
  infinite lines.  So this is a useful metaphor.


In particular, if points A and C are different colors and the line
  segment is being drawn with interpolated color, the points on the line
  segment can be colored using the mixture idea.  If A is red (1,0,0) and
  C is green (0,1,0), the point B will be:
  

    B = A(2/3) + C(1/3)

    B = (1,0,0)(2/3) + (0,1,0)(1/3)

    B = (2/3,1/3,0)




3D Parametric Line Example



Suppose we want a line from A through B, with:


A = (1,2,3)

B = (2,5,1)




We can write down the following equations:


P(t) = A+(B-A)t

P(t) = (1,2,3)+(1,3,-2)t

P(t) = (1+t, 2+3t, 3-2t)




The last equation gives another way to think about parametric equations:
by introducing a parameter (in this case, "t"), we write an equation that
generates each coordinate independently.  The equations in this example
are:


x(t) = 1+t

y(t) = 2+3t

z(t) = 3-2t





This makes it easy to see how parametric equations work so well in 3D:
each spatial coordinate (x, y, and z) is generated by a simple linear
function of just a single parameter, namely t.  None of this y=mx+b stuff
that doesn't work in 3D.


Features of Parametric Equations of Lines



Why are parametric equations so cool???




Example: Finding a Point on a Parametric Line



Problem:  Find the coordinates of a point 2/3 of the way from A=(2,3,4)
to B=(5,9,1)


Solution:  Since the point is 2/3 of the way from A to B, our parameter
is 2/3 and our starting point is A.  Our vector v is (B-A).



v = B-A = (5-2, 9-3, 1-4) = (3,6,-3)





Now, we can substitute into our equation and solve




P(2/3)= A+v(2/3)


 = (2,3,4) + (3,6,-3)(2/3) 


 = (2,3,4) + (2,4,-2) 


 = (4,7,2)





So, the point 2/3 of the way from A to B has coordinates (4,7,2).  Done!


Note that we could have solved this problem slightly differently, using
the mixture equation.  We compute a mixture of two parts B to one part A:




P(2/3)= A(1/3)+B(2/3)


 = (2,3,4)(1/3) + (5,9,1)(2/3) 


 = (2/3,1,4/3) + (10/3,6,2/3) 


 = (4,7,2)





This may seem weird at first, because we're using a weight of 1/3 on A
and a weight of 2/3 on B, but the point is closer to B, so the weight on B
has be greater.  


Problem: Suppose that vertex A is red (1,0,0) and vertex B is magenta
(1,1,0).  What is the color of the point that is 2/3 of the way from A to
B?


Solution:  We can use the same mixture equation that we just used to
find coordinates:


P(2/3) = A(1/3) + B(2/3)

P(2/3) = (1,0,0)(1/3) + (1,1,0)(2/3)

P(2/3) = (1,2/3,0)





Note if a problem calls for more than one line, each
line gets its own parameter, such as r, s, or u.  This makes sense because
the parameters have meaning: t=0 means the initial point of the line, so
s=0 would be the initial point of the other line.


Summary



These are the main points from the reading:
  



Answers





The purpose of these thought problems is to start thinking about color
interpolation.  As it turns out, the cone cells are not equally sensitive
to light.  In particular, the blue cells are less sensitive than the red
and green.  Consequently, many colors have more blue in them than you'd
think.  For example, (1,0.75,0.8) turns out to be a decent pink.