A quick trig review

In the right triangle shown below (so called because it has a right (90 degree) angle in it), we have labeled the 3 sides.
The hypotenuse is opposite the right angle of the triangle.
The height is the blue line and the base is the red line.

There are relationships between the angle of a right triangle and its base and height.

The ratio of the height to the hypotenuse is called the sine.
The ratio of the base to the hypotenuse is called the cosine.

Here's a fun demo that shows the height (or base) of a triangle as the hypotenuse swings around a circle to plot a sine (or cosine) wave.

Generating (x,y) coordinates of a circle

Let's take a circle that is centered at the point (0,0).
The radius of the circle is 1.
In the figure below, we show the X (horizontal) and Y (vertical) axis.
Angles are measured starting from the x-axis.
If we draw a line from the point (0,0) at an angle a from the x-axis, the line will intersect the circle at the point P.

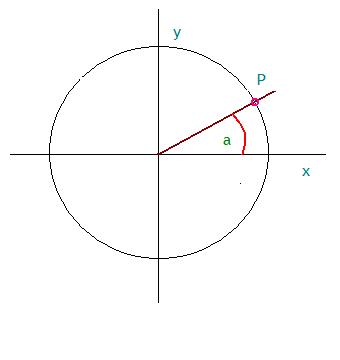
We can use the ratios above to determine the x and y coordinates of the point P. Here's how:

• The x-coordinate of P is called the cosine of a (written like this: cos(a))
• The y-coordinate of P is called the sine of a (written like this: sin(a))

Taking a closer look at generating points around a circle

To generate the coordinates along a circle, let's start with a small example.
We'll use r to refer to the radius of the circle and a to refer to the angles spanned starting from the x-axis.

Let's start with just the five following angles: 0, 90, 180, 270 and 360.
(0 and 360 degrees are the same angle, namely, the positive x-axis).

r = 1
a = 0, 90, 180, 270, 360 (angles in degrees)

Now let's look at the same angles, but show them in radians rather than degrees.

a = 0, pi/2, pi, 3pi/2, 2pi
(angles in radians, where a complete trip around the circle is 2pi)

Then, to generate the x and y coordinates along the circle, we use:

x = r * cos(a)
y = r * sin(a)

For each of the 5 values of our angle a, this gives us:

	a = 0	a = pi/2	a = pi	a = 3pi/2	a = 2pi
x =	1 * cos(0)	1 * cos(pi/2)	1* cos(pi)	1* cos(3*pi/2)	1* cos(2*pi)
x =	1 * 1	1 * 0	1 * -1	1 * 0	1 * 1
x =	1	0	-1	0	1

And we do a similar calculation for the y-coordinates using:

   y = r * sin(a)

y =	1 * sin(0)	1 * sin(pi/2)	1* sin(pi)	1* sin(3*pi/2)	1* sin(2*pi)
y =	1 * 0	1 * 1	1 * 0	1 * -1	1 * 0
y =	0	1	0	-1	0

These x and y coordinates (in the yellow boxes above), taken in pairs, do indeed give us the coordinates of the points shown in the above figure (working our way around counter-clockwise):

(1, 0)
(0, 1)
(-1, 0)
(0, -1)
(1,0)

In the above examples, we're only using 4 points, so it doesn't look much like a circle yet.
However, if we consider these 9 angles:

a = 0, pi/4, pi/2, 3pi/4, pi, 5pi/4, 3pi/2, 7pi/8, 2pi

Then, we can produces the x and y coordinates for these 9 angles:

And if we jump from 9 to 17 angles between 0 and 2pi, we can see the coordinates are approaching a circular shape.

Back to Assignment 1