Circuit Herbology
ex Grow circuits and processor components.
- Assign: Thursday, 22 September
- Due: before class Thursday, 29 September
- Submit: Bring a typed or neatly handwritten paper copy to class.
- Relevant Reference:
- Collaboration: individual ex assignment policy, as defined by the syllabus.
1. Marauder’s Map (10 points)
| A | B | C | D | F(A,B,C,D) |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Draw a Karnaugh Map for the function F defined by the truth table at right. Use the Karnaugh Map to derive a minimal sum-of-products Boolean formula for F. Show any intermediate work. Review the reading on Karnaugh Maps carefully to understand the rules, especially with respect to wrapping boxes around.
2. Encoder a.k.a. the Undecoder? (8 points)
Draw a circuit to implement a 4-to-2 encoder using gates. An encoder is the opposite of a decoder. It takes 2n inputs and provides n outputs. Here, n = 2. Assume exactly one of the inputs carries a 1 and all others carry 0. The output should be an n-bit binary number giving the index of the input that is enabled. For example, if input 2 (in the range 0-3) is enabled and all others are disabled, the output should be 1 0.
3. Moving Staircases (8 points)
Draw a circuit to implement a switching network with two data inputs (A and B), two data outputs (C and D), and a control input (S). If S is 1, the network is in pass-through mode: output C should equal input A and output D should equal input B. If S is 0, the network is in crossing mode: C should equal B, and D should equal A. Use the most reasonable combinational building blocks or gates.
4. Value Judgments (24 points)
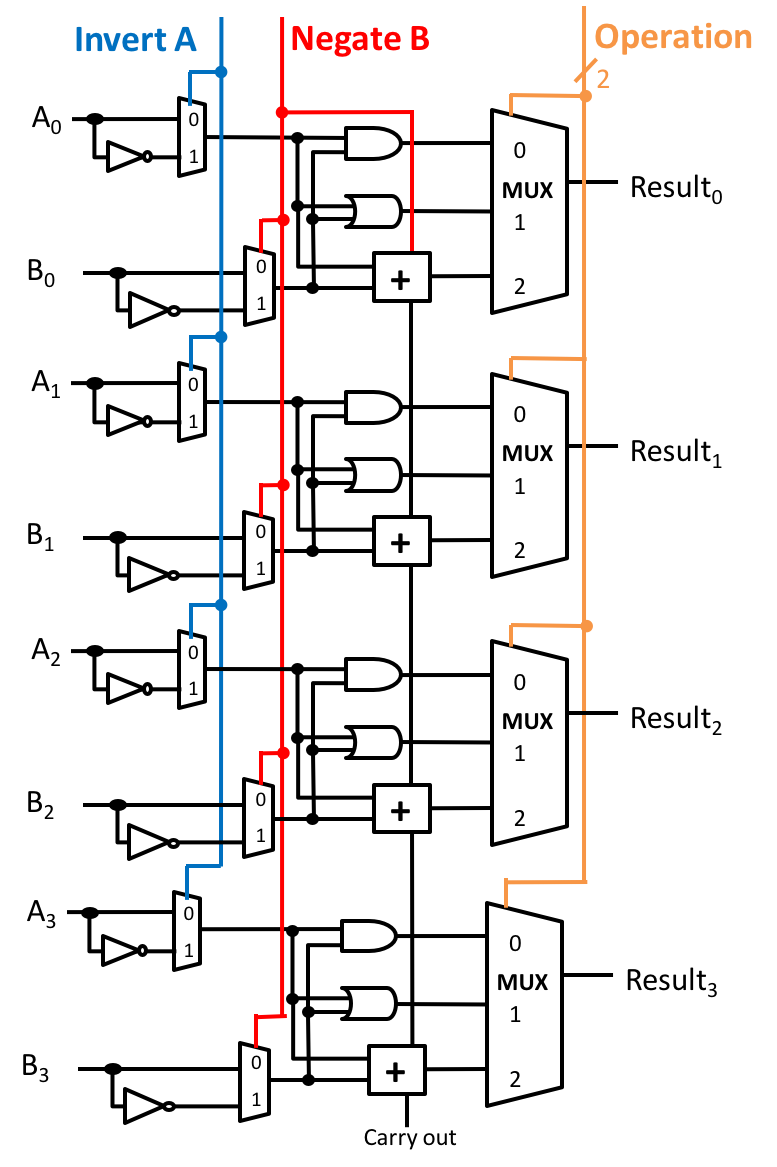
In class and lab we designed an n-bit ALU by connecting n 1-bit ALUs. In these exercises, you will improve the 4-bit version of our design.
Summary of our ALU design:
- The carry out from each bit is wired to the carry in of the next bit, if present.
- The full n-bit ALU has 4 lines of control input:
- Invert A controls the invert A inputs of all of the 1-bit ALUs.
- Negate B controls:
- the invert B inputs of all of the 1-bit ALUs; and
- the carry-in of the least significant bit ALU.
- Two bits of Operation ID control the Operation inputs of all of the 1-bit ALUs.
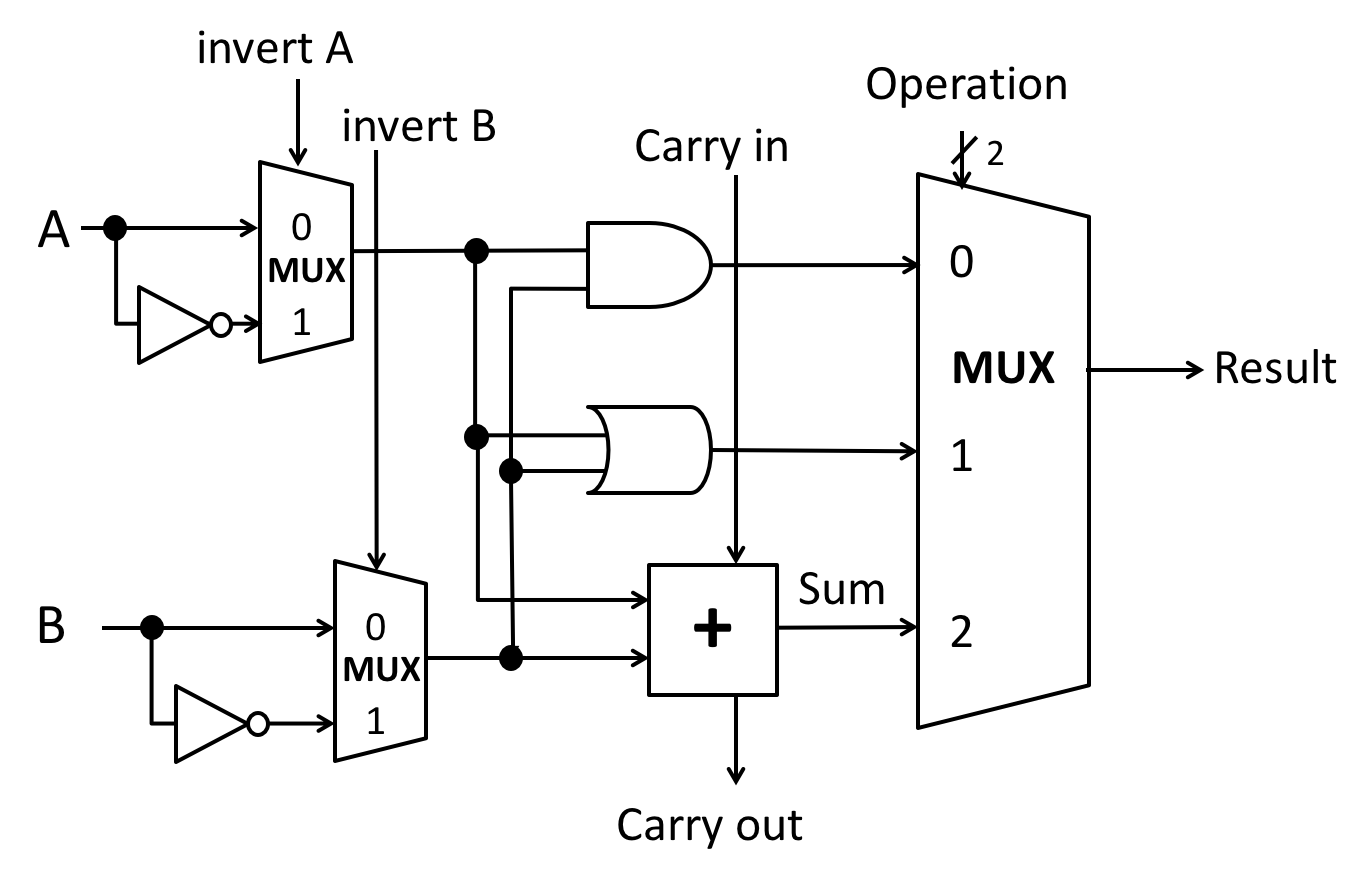
Rules for extending the ALU:
- Use the ALU sheet available here to draw logic diagrams for these exercises. There are 4 identical pages, allowing you to print 1, 2, or 4 ALUs per side.
- Any additional logic may connect to any existing wires in the ALU and add gates or other building blocks as needed.
- Minimize the number of gates or other building blocks you add.
- Choose the simplest option and clearly label new outputs.
- Feel free to draw answers for separate exercises on separate diagrams or to combine them in one diagram, as you wish.
Exercises:
-
[2 points] Design extra 1-bit outputs from the n-bit ALU for the four conditions codes (i) Zero Flag, (ii) Sign Flag, (iii) Carry Flag, and (iv) Overflow Flag. Their definitions are given in the slides on ALUs. Using the ALU sheet, draw and label the additional logic required for each condition code (flag), all on one ALU diagram. Feel free to reuse designs from your notes.
-
[6 points] Describe the output of the ALU when “Invert A” = 1, “Negate B” = 1, and “Operation ID” = 10.
- Write your answer as an arithmetic or Boolean/bitwise expression using A and B, e.g., Result = A & B or Result = 2A / B.
- Your expression must use either arithmetic operators or Boolean/bitwise operators. You may not mix them.
-
[8 points] Consider a less-than check for two’s-complement operands that computes A - B and returns a value based on the sign bit of the difference: 0 means A ≥ B, 1 means A < B.
- [1 point] Give a pair of values, A and B, where this approach correctly indicates A < B.
-
[1 point] Give a pair of values, A and B, where this approach incorrectly indicates A < B, even though actually, A ≥ B. Name the key effect that caused the answer to be incorrect.
- [6 points]
Redesign less-than so it works correctly for all pairs of
4-bit two’s-complement operands.
- Show how to control each of the 4 control lines of the full ALU.
- Using the ALU sheet, draw minimal additional logic to compute the correct less-than result as a 1-bit output of the full ALU, in the style of the condition codes you implemented above, yielding 1 if A < B and 0 otherwise.
-
[6 points] Design a 1-bit equality test output for the ALU using minimal additional logic (but no additional XOR gates). Given inputs A and B, this output wire should carry 1 if A = B and 0 otherwise. Using the ALU sheet, draw and label your design.
-
[2 points] Does the problem we encountered with less-than matter in your design of equality logic?
5. Points Affixed or Afloat in a C of Numbers (14 points)
-
[6 points] The Sea language (an imaginary programming language otherwise identical to C) supports a
signed fixed8ths chartype1 using an 8-bit signed fixed point number system with precision to the 1/8 (eighths) place.-
[1 point] What are the minimum and maximum numbers representable by a
signed fixed8ths char? Write your answer as a base ten number using fractions or decimals. -
[1 point] What are the minimum and maximum numbers representable by a
signed fixed32nds char, which uses 8-bit signed fixed-point representation with precision to the 32nds place? Write your answer as a base ten number using fractions or decimals. -
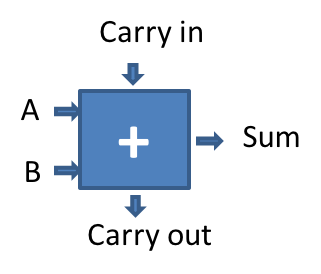
8-bit two's complement adder.
A, B, and Sum are 8-bit buses.[3 points] We provide a hardware adder design (at right) that supports 8-bit two’s complement addition (e.g., for
signed charnumbers). Draw a logic diagram for a hardware adder that supports thesigned fixed8ths charnumber system. If it is helpful, you may use the provided adder as a black box (no need to draw the internals) and extend it with whatever wiring and logic is necessary. (Warning: see (iv).) - [1 points]
What would change in your design for (iii) to support
signed fixed32nds char? What is the “trick” here? (one short phrase or sentence for both questions)
-
-
[8 points] Complete the function
float_less_or_equalwith an expression that implements a less-than-or-equal comparison on the bit representations ofxandywithout comparisons onfloat-type expressions. You may use<=and other comparison operators onunsigned-type expressions only. Otherwise, there are no restrictions on operators. The (provided) functionfloat_bitsis used to get this bit representation as anunsigned32-bit value. (Since C actually converts representations (instead of reinterpreting bits) when casting to or from floating point types, this function is difficult to implement.)You do not need to produce a C file with your code. Just write the return expression as text.
Your implementation should handle any
xandyof typefloat(IEEE single-precision floating point), including denormalized values. Review the notes from class or CSAPP 2.4 (especially 2.4.2) to for the details of this representation.
// Returns the unsigned value with the same 32-bit
// *representation* as the float argument.
unsigned float_bits(float a);
// Return true if x <= y, false otherwise.
// Assume x != NaN and y != NaN.
// Treat +0.0 and -0.0 as equal.
int float_less_or_equal(float x, float y) {
unsigned xbits = float_bits(x);
unsigned ybits = float_bits(y);
// Get the sign bits.
unsigned xsign = xbits >> 31;
unsigned ysign = ybits >> 31;
// Fill in the blank with an expression that provides the correct
// return value, based only on xbits, ybits, xsign, and ysign.
return _____________________________;
}Hint: the expression likely will not fit comfortably in one line.
Think of 4 independent conditions under which the x<=y relation
holds.
-
charis often used for characters in C, including with literal character values like'c', but it is just a number type. It is synonymous withsigned charin most implementations, just a signed 8-bit integer.unsigned charis an unsigned 8-bit integer. ↩