pencil Grow logic circuits and processor components.

Exercises

Please write your answers on the cs240-circuits-worksheet.pdf submission sheet to streamline the grading process.

1. Marauder’s Map (10 points)

$A$ $B$ $C$ $D$ $F(A,B,C,D)$
0 0 0 0 1
0 0 0 1 1
0 0 1 0 1
0 0 1 1 0
0 1 0 0 0
0 1 0 1 1
0 1 1 0 0
0 1 1 1 1
1 0 0 0 1
1 0 0 1 0
1 0 1 0 1
1 0 1 1 0
1 1 0 0 0
1 1 0 1 1
1 1 1 0 0
1 1 1 1 1
Truth table for Marauder's Map.

Draw a Karnaugh Map for the function $F$ defined by the truth table at right. Use the Karnaugh Map to derive a minimal sum-of-products Boolean formula for $F$. Show any intermediate work. Review the reading on Karnaugh Maps carefully to understand the rules, especially with respect to wrapping boxes around.

2. Encoder a.k.a. the Undecoder? (8 points)

Draw a circuit to implement a 4-to-2 encoder using gates. An encoder is the opposite of a decoder. It takes $2^n$ inputs and provides $n$ outputs. Here, $n = 2$. Assume exactly one of the inputs carries $1$ and all others carry $0$. The output should be an $n$-bit binary number giving the index of the input that is enabled. For example, if input $2$ (in the range $0..3$) is enabled and all others are disabled, the output should be $1$ $0$.

3. Moving Staircases (8 points)

Draw a circuit to implement a switching network with two data inputs ($A$ and $B$), two data outputs ($C$ and $D$), and a control input ($S$). If $S = 1$, the network is in pass-through mode: $C = A$ and $D = B$. If $S = 0$, the network is in crossing mode: $C = B$, and $D = A$. Use the most reasonable combinational building blocks or gates.

4. Value Judgments (24 points)

n-bit ALU
4-bit ALU

In class and lab we designed an $n$-bit ALU by connecting $n$ 1-bit ALUs. In these exercises, you will improve the 4-bit version of our design.

Summary of our ALU design:

  • The Carry out from each bit is wired to the Carry in of the next bit, if present.
  • The full $n$-bit ALU has 4 lines of control input:
    • Invert A controls the invert A inputs of all of the 1-bit ALUs.
    • Negate B controls:
      • the invert B inputs of all of the 1-bit ALUs; and
      • the carry-in of the least significant bit ALU.
    • Two bits of Operation ID control the Operation inputs of all of the 1-bit ALUs.
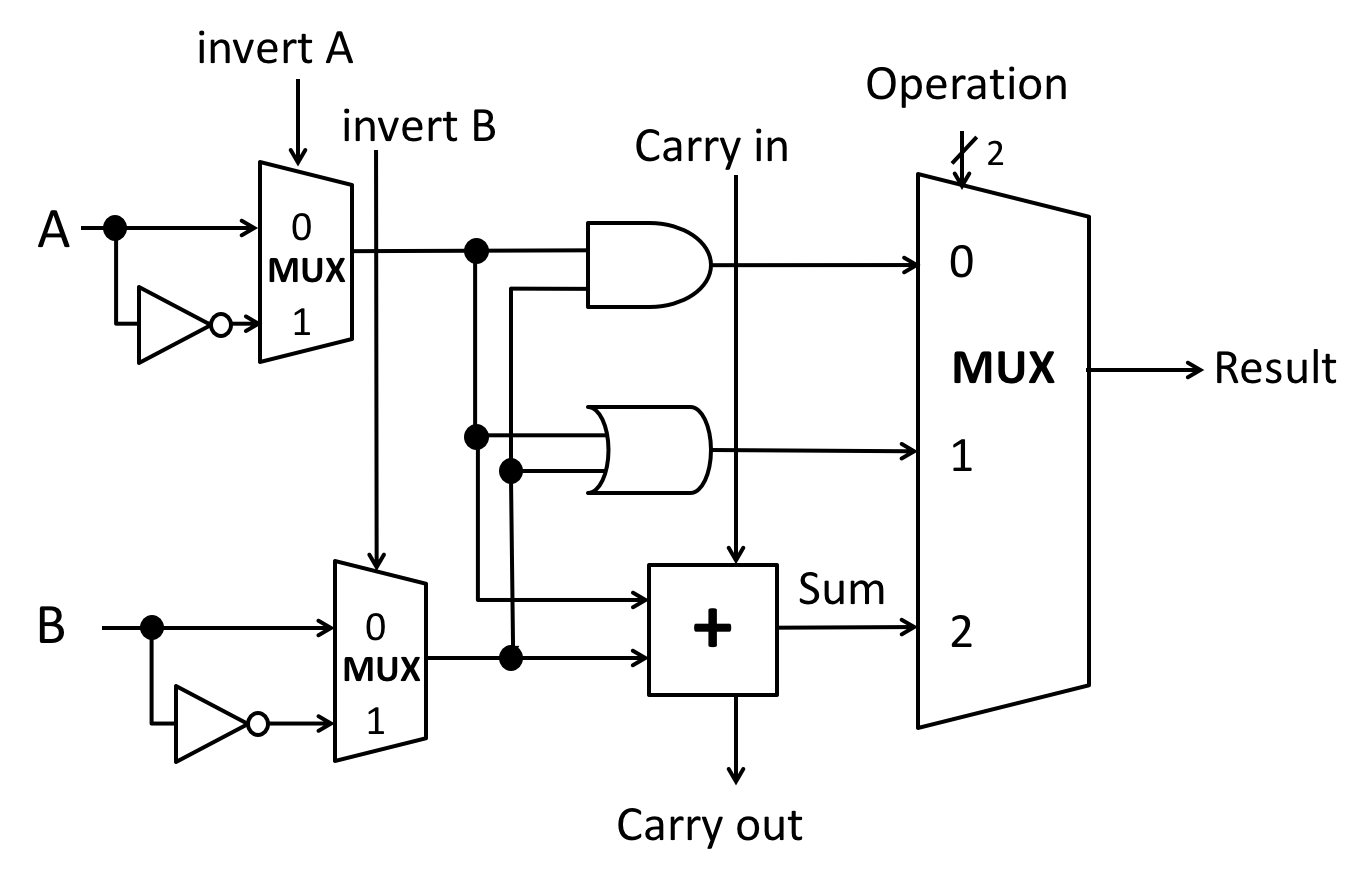
1-bit ALU
1-bit component ALU

Rules for extending the ALU:

  • Any additional logic may connect to any existing wires in the ALU and add gates or other building blocks as needed.
  • Minimize the number of gates or other building blocks you add.
  • Choose the simplest option and clearly label new outputs.
  • Feel free to draw answers for separate exercises on separate diagrams or to combine them in one diagram, as you wish.

Exercises:

  1. [2 points] Design extra 1-bit outputs from the $n$-bit ALU for the four conditions codes (i) Zero Flag, (ii) Sign Flag, (iii) Carry Flag, and (iv) Overflow Flag. Their definitions are given in the slides on ALUs. Using the provided sheet, draw and label the additional logic required for each condition code (flag), all on one ALU diagram. Feel free to reuse designs from your notes.

  2. [6 points] Describe the output of the ALU when Invert A = 1, Negate B = 1, and Operation ID = 10.
    • Write your answer as an arithmetic or Boolean/bitwise expression using $A$ and $B$, e.g., Result = $A \& B$ or Result = $\frac{2A}{B}$.
    • Your expression must use either arithmetic operators or Boolean/bitwise operators. You may not mix them.

  3. [8 points] Consider a less-than check for two’s-complement operands that computes $A - B$ and returns a value based on the sign bit of the difference: 0 means $A \geq B$, 1 means $A < B$.

    1. [1 point] Give a pair of values, $A$ and $B$, where this approach correctly indicates $A < B$.

    2. [1 point] Give a pair of values, $A$ and $B$, where this approach incorrectly indicates $A < B$, even though actually, $A \geq B$. Name the key effect that caused the answer to be incorrect.

    3. [6 points] Redesign less-than using minimal additional logic to compute the correct less-than result for all pairs of 4-bit two’s-complement values. Provide a 1-bit output of the full ALU in the style of the condition codes you implemented above, yielding 1 if $A < B$ and 0 otherwise.
      • Show how to control each of the 4 control lines of the full ALU.
      • Using the provided sheet, draw and label your design.
  4. [5 points] Design a 1-bit equality test output for the ALU using minimal additional logic (but no additional XOR gates). Given inputs $A$ and $B$, this output wire should carry 1 if $A = B$ and 0 otherwise.
    • Show how to control each of the 4 control lines of the full ALU.
    • Using the provided sheet, draw and label your design.
  5. [3 points] Consider the similarities and differences in the workings of your designs for less-than and equals. Does the problem we encountered with less-than matter in your design of equality logic? Briefly explain why or why not.