• Assign: Tuesday, 4 September
• Due: In class or under the door of Ben's office (SCI S580) by 11:59pm on Tuesday, 11 September
• Policy: Individual graded synthesis assignment
• Submit: A neat paper copy of the cs240-gates-worksheet.pdf submission sheet .
• Reference:
  • digital logic
  • Boolean Laws

Exercises

Please write your answers on the cs240-gates-worksheet.pdf submission sheet to streamline the grading process.

1. [3 points] Write truth tables and unsimplified Boolean expressions for each of the output signals $F_1$ and $F_2$ in the following circuit. Create the boolean expressions via a direct translation of the circuit.

   

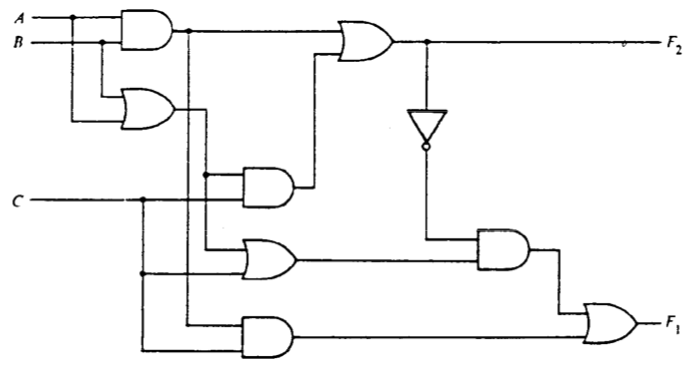
2. [6 points] Draw unsimplified circuits to implement the following Boolean expressions. We use the apostrophe$’$ notation as an alternative to the overbar to indicate logical negation of the preceding term. The apostrophe binds tightly. For example, $AB’$ means $(A)(B’)$.

   1. $(A + B)(A + B’)$
   2. $ABC + A’B + ABC’$
   3. $A’B’ + A’BC’ + (A + C’)’$

3. [5 points] Write a Boolean expression and draw a circuit in sum-of-products form for the output $Y$ of this truth table.

   $A$	$B$	$C$		$Y$
   0	0	0		1
   0	0	1		0
   0	1	0		1
   0	1	1		0
   1	0	0		1
   1	0	1		1
   1	1	0		0
   1	1	1		1

4. [15 points] Using elementary rules of Boolean algebra, find the simplest equivalent of the Boolean expressions below using only products, sums, and negation (i.e., no XOR). Show your derivation step by step. Label each step with the name of the rule you apply. You may find this sheet of Boolean laws useful.

   1. $(A + B)(A + B’)$
   2. $ABC + A’B + ABC’$
   3. $A’B’ + A’BC’ + (A + C’)’$
   4. [Harder!] $A’B’C’D’ + AB’C’ + AB’CD’ + ABD + A’B’CD’ + BC’D + A’$

5. [6 points] Draw two circuits that implement two-input XOR:

   1. Using only 2-input NAND gates.
   2. Using only 2-input NOR gates.

   In both circuits, use the smallest number of gates you can.