Gates

Assignment: Gates

• Assign: Wednesday 8 September
• Due: Tuesday 14 September
• Policy: Individual graded synthesis assignment
• Submit: Upload a PDF written on the cs240-gates-worksheet.pdf submission sheet
• Reference:
  • Digital Logic
  • Boolean Laws

Contents

• Assignment: Gates
• Exercises
  • 1. Circuit to Expression (3 points)
  • 2. Expression to Circuit (6 points)
  • 3. Sum of Products (5 points)
  • 4. Simplification (15 points)
  • 5. XOR from Universal Gates (6 points)
• Submission

Exercises

Please write your answers on the cs240-gates-worksheet.pdf submission sheet to streamline the grading process. Submit your work by scanning a PDF of all worksheet pages (in order) and uploading it to Gradescope. Remember that this course uses your Gradescope account attached to your Wellesley email address (the variety that matches your username). You can merge accounts across multiple email addresses if helpful.

1. Circuit to Expression (3 points)

Write truth tables and unsimplified Boolean expressions for each of the output signals $F_1$ and $F_2$ in the following circuit. Create the boolean expressions via a direct translation of the circuit.

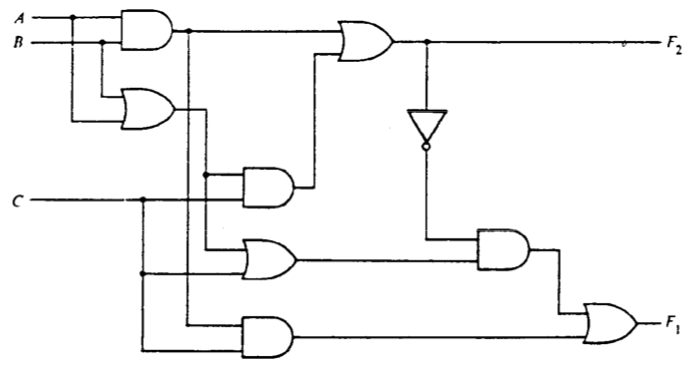
2. Expression to Circuit (6 points)

Draw unsimplified circuits to implement the following Boolean expressions. We use the apostrophe$’$ notation as an alternative to the overbar to indicate logical negation of the preceding term. The apostrophe binds tightly. For example, $AB’$ means $(A)(B’)$. Use many-input AND, OR, NOR, or NAND gates where they are useful (instead of using only 2-input gates).

1. $(A + B)(A + B’)$
2. $ABC + A’B + ABC’$
3. [Independent] $A’B’ + A’BC’ + (A + C’)’$

3. Sum of Products (5 points)

Write a Boolean expression and draw a circuit in sum-of-products form for the output $Y$ of this truth table. Use many-input AND and OR gates where useful (instead of using only 2-input gates). Give a direct translation of the truth table to a sum of products without simplifying.

$A$	$B$	$C$		$Y$
0	0	0		1
0	0	1		0
0	1	0		1
0	1	1		0
1	0	0		1
1	0	1		1
1	1	0		0
1	1	1		1

4. Simplification (15 points)

Using elementary rules of Boolean algebra, find the simplest equivalent of the Boolean expressions below using only products, sums, and negation (i.e., no XOR). Show your derivation step by step. Label each step with the name of the rule you apply. You may find this sheet of Boolean laws useful.

1. $(A + B)(A + B’)$
2. $ABC + A’B + ABC’$
3. [Independent] $A’B’ + A’BC’ + (A + C’)’$
4. [Independent. This one is harder and serves as a teaser to motivate a useful technique we will learn later. Give it a try, but do not be concerned if you think you are stuck. ] $A’B’C’D’ + AB’C’ + AB’CD’ + ABD + A’B’CD’ + BC’D + A’$

5. XOR from Universal Gates (6 points)

Draw two circuits that implement two-input XOR:

1. Using only 2-input NAND gates.
2. [Independent] Using only 2-input NOR gates.

In both circuits, use the smallest number of gates you can. Generally, this problem may require trial and error. You are not expected to know an elegant strategy for it ahead of time.

Submission

Please write your answers on the cs240-gates-worksheet.pdf submission sheet to streamline the grading process. Submit your work by scanning a PDF of all worksheet pages (in order) and uploading it to Gradescope. Remember that this course uses your Gradescope account attached to your Wellesley email address (the variety that matches your username). You can merge accounts across multiple email addresses if helpful.