▲ ☰ ▼

CS 240 Lab 4

ALU & Sequential Logic

CS 240 Lab 4

In lab today, you will investigate the circuit which allows you to perform a variety of logical and arithmetic operations, the Arithmetic and Logic Unit (ALU), which is an essential part of a computer processor.

You will also investigate the behavior of several sequential logic circuits, which form the basis for the various kinds of memories needed to implement a computer.

If you want to work in CircuitVerse today, download this project file and use the different tabs for each part of the lab. Use this link to open CircuitVerse

Arithmetic Logic Unit

An Arithmetic Logic Unit (ALU) is a combinational circuit used to perform all the arithmetic and logical operations for a computer processor, and can be built using basic components that you are familiar with.

You saw a very simple ALU on the lab assignment. The circuit below also uses an additional set of 2x1 multiplexers at the inputs, controlled by new control lines “Invert A,” “Invert B, and it has a”Carry in” line.

“Invert A” allows you to invert the A input (for logical operations), and “Invert B” does the same for the B input.

“Carry in” allows you to add a carry-in bit to the adder, and when combined with “Invert B,” this lets you do subtraction, since (~B + 1) = -B, and thus A + (~B + 1) = A - B.

In the following circuit, the box with + is a 1-bit adder. The “invert B” and “Carry in” inputs have been combined into one “Negate B / Carry-in” input. Assume Operation is a 2-bit value Op1 Op0.

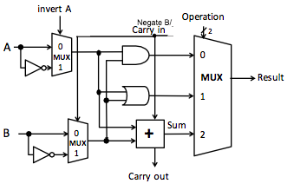
Circuit diagram of an ALU. On the left, input values are A and B. At the top, inputs “invert A,” “Negate B/Carry in,” and Operation are present. An output “Result” goes to the right, and an output “Carry out” exits downwards. For both the A and B inputs, the wire splits and one side goes into a NOT gate. Then both the normal and inverted signals for each input go into a 2x1 mux. The “invert A” input controls the mux for the A input, and the “Negate B/Carry in” input controls the mux for the B input. That input also gets fed into the adder as the carry-in bit. In the middle of the circuit, in addition to the aforementioned adder at the bottom, there is one AND gate at the top and one OR gate in the middle. Both of these gates take the multiplexed A and B inputs as their inputs, and the adder does as well. The outputs from the AND gate, the OR gate, and the adder all feed into a final multiplexer, whose select bits are hooked up to the “Operation” input (which has 2 bits, not just one). The output of that multiplexer is the result output for the entire circuit. 

The basic operations are:

Operation Explanation
add A + B + Carry in
sub invert B = 1, Carry in = 1, then add
AND A AND B
OR A OR B
NOR invert A=1, invert B=1, then AND
NAND invert A=1, invert B=1, then OR

The following partial truth table shows the inputs necessary to enact each of these operations. Note the clever use of DeMoragn’s law to get NAND and NOR operations. Also note that we can use one column for both “invert B” and “Carry in” because their values can be the same in every row.

invert A invert B/Carry in Op1 Op0 Result
0 0 0 0 A AND B
0 0 0 1 A OR B
0 0 1 0 A + B
0 1 1 0 A – B
1 1 0 0 A NOR B
1 1 0 1 A NAND B

Exercise 1:

Predict the results for this circuit (the answers to the first combination of inputs are shown; click in the Cout and Result columns to cycle through answers):

A B invA invB/Cin Op1 Op0 Cout Result Check Description
0 0 0 0 0 0 0 0 Result: 0 (0 AND 0)
Cout: 0 (0 + 0 has no carry-out)
GCorrect answer: 0 1 0 0 0 1 0
 1
 0
 1
 Correct answer: See above Example answer:
Result: 1 (0 OR 1)
Cout: 0 (0 + 1 has no carry-out)
GCorrect answer: 0 1 0 0 0 0 0
 1
 0
 1
 Correct answer: See above Example answer:
Result: 0 (0 AND 1)
Cout: 0 (0 + 1 has no carry-out)
GCorrect answer: 1 1 0 0 1 0 0
 1
 0
 1
 Correct answer: See above Example answer:
Result: 0 (1 + 1)
Cout: 1 (1 + 1 has carry-out)
GCorrect answer: 0 1 0 1 1 0 0
 1
 0
 1
 Correct answer: See above Example answer:
Result: 1 (0 + 0 w/ carry-in)
Cout: 0 (0 + 0 + carry-in has no carry-out)
GCorrect answer: 1 1 0 0 0 0 0
 1
 0
 1
 Correct answer: See above Example answer:
Result: 1 (1 AND 1)
Cout: 1 (1 + 1 has carry-out, even though that’s not the operation we care about)
GCorrect answer: 1 1 1 1 0 0 0
 1
 0
 1
 Correct answer: See above Example answer:
Result: 0 (0 AND 0 since A and B are inverted)
Cout: 0 (0 + 0 + carry-in has no carry-out)

Download this aluparts.cct circuit and then open it in LogicWorks, or work in the Falstad window below, or work in the “ALU Parts” tab of the Circuitverse project (see link above). Build a 1-bit ALU by connecting the provided parts together.

Note: In the Falstad simulator you can hover over a component to see its name.

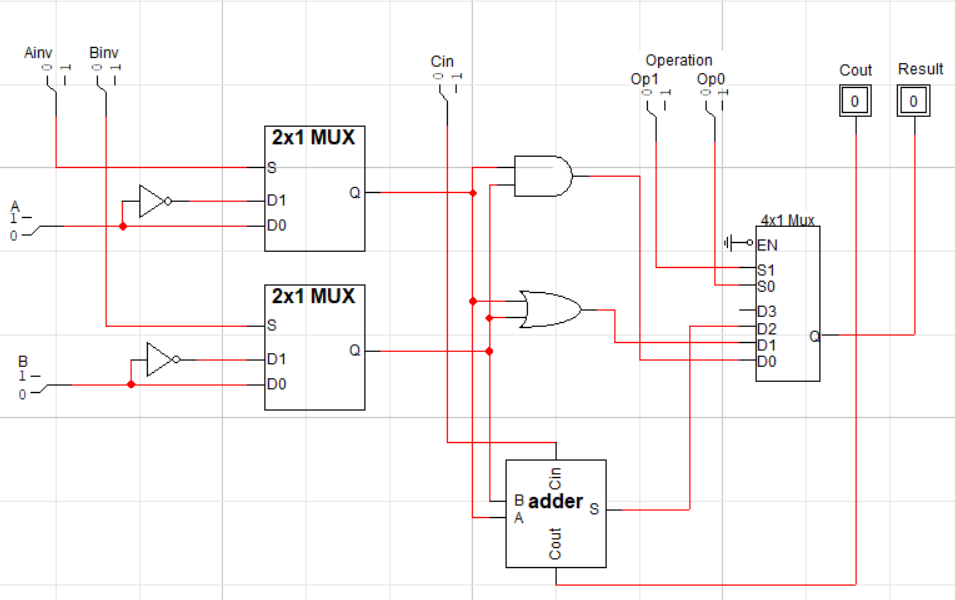
Verify your predicted results by setting the inputs from the table above and checking that the outputs match what you expected. Click this button to show the intended connections if you get stuck:

Example answer:

Here’s what the connections should look like in LogicWorks (with some extra binary probes to show intermediate values):

LogicWorks screenshot showing correct connections for the ALU parts: Ainv is connected to the S input on the top 2x1 mux. Binv is connected to the S input on the bottom 2x1 mux Cin is connected, to the carry-in line of the adder. A is connected to the D0 input of the top mux, and to the NOT gate for that mux, whose output connects to its D1. B is connected to the D0 input of the bottom mux, and to the NOT gate for that mux, whose output connects to its D1. The top mux output connects to the top inputs of the AND gate and the OR gate, and to the A input of the adder. The bottom mux output connects to the bottom inputs of the AND gate and the OR gate, and to the B input of the adder. The mux outputs and the adder carry-in each have extra binary probes attached to show their values. The outputs from the AND gate, the OR gate, and the adder connect to the D0, D1, and D2 inputs to the 4x1 mux, respectively. Its D3 input is not connected. The Op0 and Op1 inputs connect to the S0 and S1 inputs of the 4x1 multiplexer, and its enable line (which is active low) is connected to ground. The Q output of the 4x1 mux is connected to the Result binary probe, while the carry-out from the adder is connected to the Cout binary probe. 

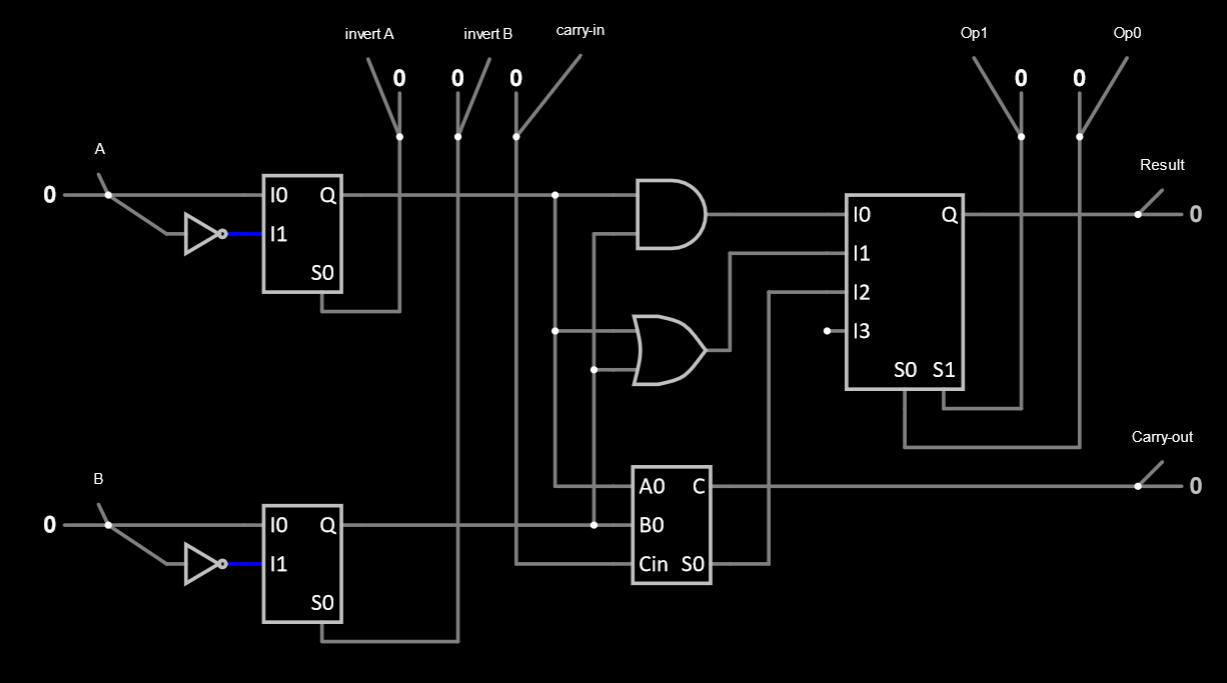
Here’s what they should look like in Falstad:

Falstad screenshot showing the parts hooked together: The A input is connected to both the I0 input of the top 2x1 mux and the NOT gate which connects to the I1 input. The B input is likewise connected to the I0 and I1 inputs of the bottom 2x1 mux with a NOT gate on the I1 path. The “invert A” input is connected to the S0 input of the top 2x1 mux. The “invert B” input is connected to the S0 input of the bottom 2x1 mux. The “carry-in” input is connected to the Cin input of the adder. The Q output of the top 2x1 mux connects to the top inputs of the AND gate, the OR gate, and the adder (labeled A0 on the adder). The Q output of the bottom 2x1 mux connects to the bottom inputs of the AND gate, the OR gate, and the adder (labeled B0 on the adder). The AND gate output connects to the I0 input of the 4x1 mux. The OR gate output connects to the I1 input of the 4x1 mux. The adder S0 output connects to the I2 input of the 4x1 mux. The I3 input of the 4x1 mux is not connected. The Op0 input connects to the S0 input of the 4x1 mux. The Op1 input connects to the S1 input of the 4x1 mux. The Q output of the 4x1 mux connects to the Result output. The C output of the adder connects to the Carry-out output. 

Exercise 2:

It is possible to make a 4-bit ALU by connecting four 1-bit ALUs together in a similar way to how you connected 4 1-bit adders to make a 4-bit adder in lab last week (for this they need separate invert-B and carry-in inputs):

Without testing it in the simulator above, predict the results for this 4-bit ALU in the table below, taking into account:

  • A and B are 4-bit values represented by hex digits, and are signed two’s complement representations. Use this hex reference to help you translate between hex, binary, and decimal.
  • The Result is a 4-bit value and should be written as a hex digit.
  • Cout, Sign, and Overflow are single bits.
  • Cout and Overflow are produced according to the addition operator, even when the circuit is performing a different operation.

The definitions for each column are:

  • Result is the result for the selected operation.
  • Cout is the carry-out bit from addition. This is always computed by the adder, whether or not the operation is addition.
  • Sign is the sign bit of the result (the most-significant bit).
  • Overflow is true if there’s overflow from the adder (assuming signed two’s-complement numbers). Overflow is always computed by the adder, whether or not the operation is addition.
  • Zero should be true if and only if the result is exactly 0.
Function Test Inputs Result
(in hex)		 Cout Sign Overflow Zero Check
A + B A=3, B=7 A 0 1 1 0
GCorrect answer: A + B A=F, B=E Correct answer: D 0
 1
 0
 1
 0
 1
 0
 1
 Correct answer: See above
GCorrect answer: A AND B A=1, B=F Correct answer: 1 0
 1
 0
 1
 0
 1
 0
 1
 Correct answer: See above
GCorrect answer: A AND B A=7, B=8 Correct answer: 0 0
 1
 0
 1
 0
 1
 0
 1
 Correct answer: See above
GCorrect answer: A OR B A=3, B=C Correct answer: F 0
 1
 0
 1
 0
 1
 0
 1
 Correct answer: See above
GCorrect answer: A NOR B A=6, B=9 Correct answer: 0 0
 1
 0
 1
 0
 1
 0
 1
 Correct answer: See above
GCorrect answer: A - B A=3, B=4 Correct answer: F 0
 1
 0
 1
 0
 1
 0
 1
 Correct answer: See above
GCorrect answer: A - B A=C, B=9 Correct answer: 3 0
 1
 0
 1
 0
 1
 0
 1
 Correct answer: See above
GCorrect answer: A + B A=5, B=4 Correct answer: 9 0
 1
 0
 1
 0
 1
 0
 1
 Correct answer: See above

Exercise 3:

Given the simulated 4-bit ALU above, describe the underlying connections/logic needed to produce the Sign, Overflow, and Zero outputs (including any gates that are required).

Sign bit:

Example answer: The sign bit is wired to the most-significant bit of the 4 output lines, which is the sign bit in two’s-complement arithmetic.

Overflow bit:

Example answer: The more complex way is to do (NOT(A3 XOR B3)) AND (A3 XOR R3). This breaks down into NOT(A3 XOR B3) which is true when A3 is the same as B3, along with A3 XOR R3 which is true when A3 is different from R3. In other words: “Signs were the same going in, but we got the opposite sign coming out.” An easier way to implement this is to just XOR the carry-in and carry-out for the last 1-bit ALU. That works because if there’s carry-in, there will be carry-out unless both sign bits are 0, in which case there must be overflow since we had two zeroes going in but a carry means a 1 will go out. On the other hand, if there’s no carry-in, there can only be carry-out if both sign bits were 1’s, meaning we added two negative numbers and due to carry-out ended up with a positive number.

Zero bit:

Example answer: The Zero bit is wired to the result of a 4-input NOR gate (or several 2-input OR gates with a NOT gate at the end to emulate a 4-input NOR) that takes all 4 bits of output as its inputs. That way, the Zero bit is 1 when the value of the output is exactly 0000₂, and 0 otherwise.

Exercise 4:

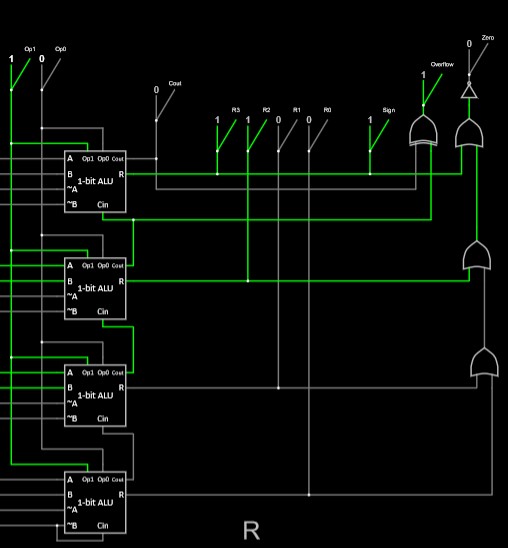
Now add the gates you just described to the simulator above, so that in addition to result and carry outputs, it has 1-bit outputs for Sign, Overflow, and Zero.

Verify that your outputs work by comparing against the table above, then check your design against the example below.

Example answer:

Here’s what the additional outputs should look like:

The right-hand side of the 4-bit ALU, showing the Operation input lines but not the negate lines or inputs. Circuits have been built to the right to implement the inputs or negate lines. The 4 1-bit ALU outputs connect to the result and Cout outputs as usual, but include additional circuitry to create Sign, Overflow, and Zero bits. The Sign bit is attached to the same wire as R3. The Overflow bit is the result of an XOR gate whose inputs are the carry-in and carry-out for the 4th 1-bit ALU (the one whose output is R3). The Zero bit is connected to a NOT gate, behind which there are a series of 3 OR gates that work to combine all four R0-R3 outputs so that if any of them is on, the input to the NOT gate is on, and thus the Zero bit will be 0. 

SR Latch

The SR latch is the basic unit of memory in most modern computers:

S means set the output to 1, and R means reset the output to 0. The two outputs Q and Q’ should always be opposites of each other.

Qp is the previous state of the latch. If you neither set or reset the circuit, it remembers its previous state. This means it is a bistable circuit: it has two stable voltage configurations, and external input can force it to swap between them.

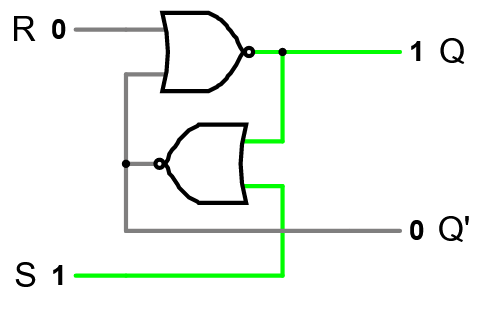
Circuit diagram for an SR latch, showing two NOR gates whose inputs each feed back into the other. Besides these feedback lines, the top NOR gate takes input from R, and sends output to Q. The bottom NOR takes its second input from S, and sends output to Q’ 

S R Q Q’
0 0 Qp Qp’
0 1 0 1
1 0 1 0
1 1 0 0

Exercise 5:

Build this circuit on your workbench, using:

  • 1 7402 NOR chip (inserted at top right)
  • two logic switches as inputs to S and R
  • two logic indicators as outputs Q and Q’

Here is the pinout for the 7402:

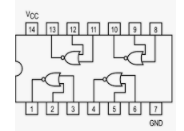
Pinout for the 7402 with 7 pins to a side numbered counterclockwise around the chip from the bottom-left next to the notch on the left. It shows Vcc on pin 14, ground on pin 7, and four NOR gates. These gates have inputs and outputs as follows: Pins 2 and 3 are inputs to a gate with output at pin 1, pins 5 and 6 are inputs to a gate with output at pin 4. Likewise pins 8 and 9 are inputs with output at pin 10, and pins 11 and 12 are inputs with output at pin 13. 

First, plan out how you will connect the circuit, by filling in the following table:

Purpose Comes from Connect to Check row
R input logic switch pin 2 N/A
Q output GCorrect answer: …
 pin 1
 pin 2
 pin 3
 pin 4
 pin 5 and …
 logic indicator
 pin 3
 pin 4
 pin 6
 Correct answer: See above
S input GCorrect answer: …
 pin 1
 logic switch
 pin 4
 …
 pin 3
 pin 4
 pin 6
 Correct answer: See above
Q’ output GCorrect answer: …
 pin 1
 pin 2
 pin 3
 pin 4
 …
 pin 3
 pin 4
 pin 5
 and logic indicator		 Correct answer: See above

Verify the circuit by following these steps:

  1. Set S=1 and R=0. What is Q? 0
     1

  2. Now set S=0 and R=0. What is Q? 0
     1

  3. Now set R=1, leaving S=0. What is Q? 0
     1

  4. Set R back to 0, leaving S=0. What is Q? 0
     1

    Why doesn’t Q return to 1, the value it had last time S=0 and R=0?

    Example answer: Since the most recent value was Q=0, and we’ve only turned off inputs since then, without a reason to swap to the other stable configuration, the circuit stays in the one it’s in, where Q=0.

  5. Now set both S=1 and R=1. What happens to Q and Q’?

    Example answer: They’re both set to 0, since both NOR gates have an active input. This violates the design principle that they should be opposites.

  6. Now set S=0 and R=0, and turn off the board, then turn it back on. What is the value of Q? Explain why the answer to that question is complicated:

    Example answer: Since the board was powered off, the remembered value gets cleared out (all wires return to neutral voltage). When you power it on, neither NOR gate has high-voltage inputs, since R=0 and S=0, and the feed-back connection isn’t high-voltage to start with. Both gates will try to activate simultaneously, since NOR logic dictates their output should be high if both inputs are off. This sends power to one input of both gates, and so they then both try to deactivate, restarting the cycle. Practically, one of them will be slightly faster to activate eventually, preventing the other gate’s signal from flipping and thus stabilizing the circuit. But we can’t easily predict which one it will be, since it might depend on factors like precise manufacturing details of the chip, temperature of the two specific gates used in the chip, humidity, etc.

Don’t disconnect your circuit! You use it in the next exercise.

Clocked SR Latch

Note: Skip this exercise if you’re making up for Lake Day.

Certain circuits require that the action of the latches in the circuit occur simultaneously, and that they can wait to receive updates until other parts of the circuit have time to settle. This can be accomplished through synchronization with a common clock input.

Exercise 6:

Modify your previous circuit so that it is a clocked SR latch:

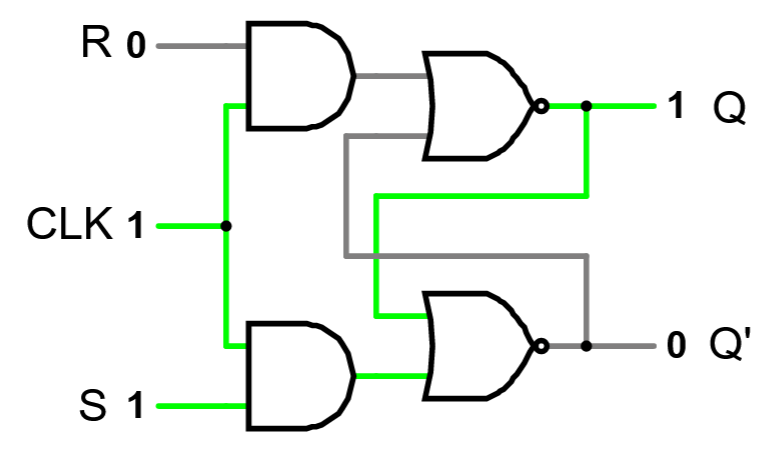
An SR Latch (the double-NOR version from before) with an additional clock input on the left. Each of the S and R inputs is now connected via an AND gate with this clock input to where it was before. 

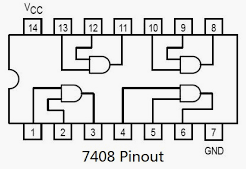
You will need to connect to a 7408 AND chip, using switch PB1 or PB2 as your clock. The 7408 chip is inserted BELOW the 7402 chip you wired in the previous exercise, and uses the following pin-out:

Pinout for the 7408 showing pins 1-14, 7 on each side of the chip numbered counter-clockwise from the top-left (with the notch at the top). Pin 14 is Vcc and pin 7 is ground. The chip has four AND gates inside, each with two input pins and one output pin. The gates are arranged so that: 1 and 2 feed 3, 4 and 5 feed 6, 10 and 9 feed 8, and finally 13 and 12 feed 11. 

Verify the correct operation of the latch as follows:

  1. Without pushing the clock button, set S=0 and R=0. Then flip through all four combinations of S and R. Why didn’t the outputs change?

    Example answer: Without the clock on, the latch part just sees both inputs as 0s, since neither AND gate activates.

  2. Set S=1 and R=0, then push and release the clock button. What is the value of Q? 0
     1

  3. Now set S=0 and R=1, and push the clock button again. What is the value of Q? 0
     1

    Did Q change when the button was pressed in, or when it was released (test again if you need to)? When it was pressed (rising edge).
     When it was released (falling edge).

  4. Now set S=0 and R=0, and push the button. What is the value of Q? 0
     1

  5. Without pressing the clock, flip S on and then off again. When it’s off, press the clock. Did Q’s value change? no
     yes

  6. Set S=1 and R=1, and push and hold the button. Observe the value of Q while holding the button, and then release it. Explain why you cannot predict the value of Q after the button is released:

    Example answer: This is the same situation as before, where with both NOR gates inactive due to active inputs from S and R, if you simultaneously turn those inputs off (such as by turning off the clock signal that’s connected to both), the system enters an unstable state. Whichever gate activates faster will stabilize it, but it’s not easy to predict which gate will win.

D Latch and Flip-Flop

The SR latch should only ever receive inputs 00, 10, and 01. 11 is problematic because it sets both Q and Q’ to 0, and because if we transition from 11 to 00, the outcome is unpredictable. The D latch makes a 11 input to the latch portion impossible, by using a single D input instead of S and R inputs, along with a clock. Here’s a circuit diagram for a D latch:

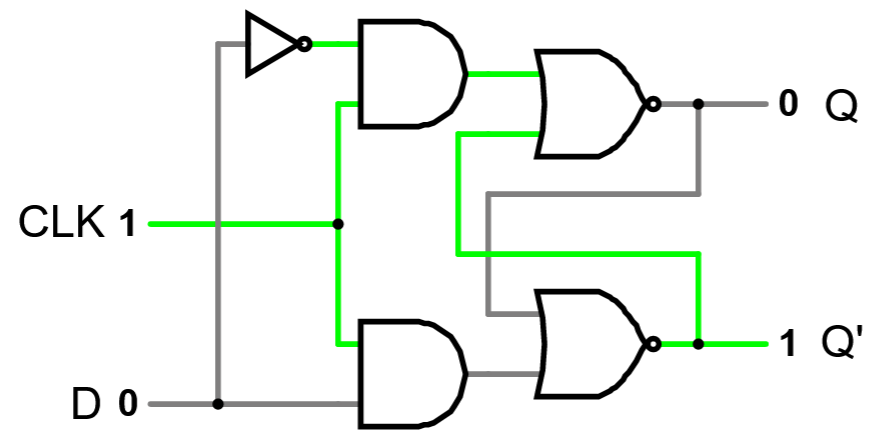
A D latch circuit diagram, with the same setup as a clocked SR latch, except that instead of two S and R inputs, there’s one D input which feeds into the old S directly and into the old R through a NOT gate. 

Note: The “CLK” input above is not an actual clock element, it’s just a logic input labeled “CLK.” We do this so that we can have manual control over when the clock shifts, instead of having to work around a constantly changing real clock.

Exercise 7:

Implement the clocked D latch circuit in LogicWorks, or in the Falstad simulator (or in CircuitVerse using the “D Latch (blank)” tab):

When you first connect the circuit, it will be in an unpredictable state. Pulse the clock once to achieve valid inputs.

Verify your circuit by following these steps:

  1. Set D to 0, and CLK to 1; then set CLK back to 0. What is the value of Q? 0
     1
  2. Set D to 1. Does Q change? no
     yes
  3. Set CLK to 1. What is the value of Q? 0
     1
  4. Now set CLK back to 0. Does the value of Q change? no
     yes

What inputs should be used to set or reset the output, and what inputs can be used to remember the previous output?

Example answer: When you turn the clock on, set D to 1 to set the output, and set D to 0 to reset the output. Turning the clock off remembers the most recent setting, even when D changes.

Explain why this circuit solves the problem of S=R=1:

Example answer: The D input is sent to each AND gate but one of the lines is inverted, so it can ONLY send the equivalent of S=1/R=0 or S=0/R=1. This isn’t useful without the clock mechanism, as it wouldn’t be able to send S=0/R=0, but when the CK input is off, the latch gets S=0/R=0 and remembers the most recent state.

Exercise 8:

A D latch will change its state each time D changes, as long as the clock remains on. However, it would be even better to have a circuit which can “observe” D only for an instant, and then remember it the rest of the time. This is called a D flip-flop, and it changes its state only at the falling edge of the clock, remembering that observed state at all other times.

Next, construct a D flip-flop with a falling-edge trigger in one of the two simulators (or using the “D flip-flop parts” tab in CircuitVerse):

In LogicWorks, it should look like this (using two “D Latch” ICs from the parts window):

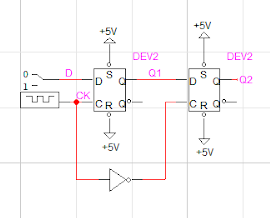
Circuit diagram of a D flip-flop in LogicWorks. On the left, there is a binary switch labeled D above a clock labeled CK. These feed into the D and C inputs of a D latch. The S and R inputs on the top and bottom are both connected to +5V (and are both marked active-low). The Q’ output of the D latch is disconnected, but the Q output feeds into the D output of a second D latch. This latch’s C input connects back to a NOT gate beneath the first D latch, whose inputs is connected to the CK clock output. This D latch also has S and R connected to +5V, and a disconnected Q’. The Q of the second D latch is labeled Q2. 

Note: It is necessary to set the S and R inputs high, as shown in the diagram.

You’ll also have to label the D input, the clock, and the Q1 intermediate output and Q2 final output.

In the Falstad simulator, it should look like this (hook things up in the window below where we’ve laid out the components you’ll need):

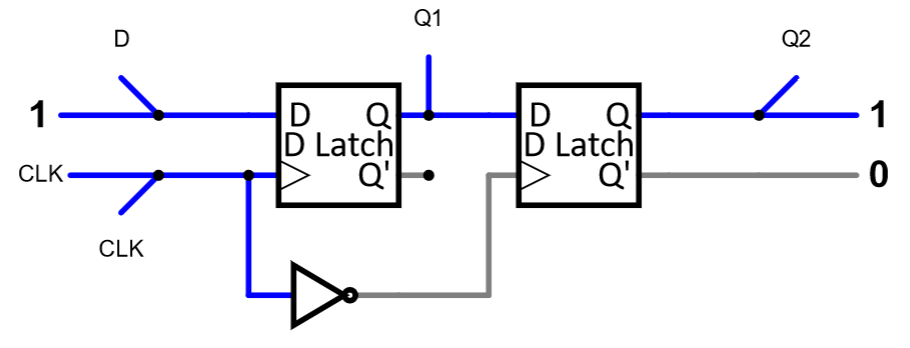
Circuit diagram of a D flip-flop in the Falstad simulator. On the left, there is a logic input labeled D, and a clock labeled CLK. These connect to the D and clock inputs of a D Latch (the clock input is indicated with a triangle pointing into the IC). The Q’ output of the D latch is disconnected, but the Q output is labeled Q1 and feeds into the D input of a second D latch. The clock input of this second latch comes from a NOT gate, whose input connects back to the same clock input feeding the first D latch. The second D latch has both outputs connected to logic outputs with the top one labeled Q. 

Use the timing window in LogicWorks or the scopes in the Falstad simulator to observe the behavior of the circuit over time, and answer these questions:

  1. Toggle the D input off, and wait until Q2 becomes 0.
  2. Try to quickly toggle the D input on and then off in such a way that the Q1 input never changes. When is this possible? Example answer: When the clock input is low, toggling the D input does not affect Q1 or Q2, so if you toggle D on and then back off before the clock input turns on again, Q1 will not change.
  3. Now try to quickly toggle the D input on and then off so that Q1 changes to a 1 and then back to a 0, without ever changing Q2. When is this possible? Example answer: When the clock input is high, D directly affects Q1, but Q1 does NOT affect Q2. So during the on phase of the clock, you can toggle D1 on and then back off, which will also toggle Q1 for the same duration, but Q2 will not be affected.
  4. Now turn D on and keep it there. When does the Q2 output change, relative to the clock signal? Example answer: It changes on the next falling edge of the clock that occurs after the D signal becomes a 1.
  5. Now turn D off again, and observe when Q2 turns off. When does it change, relative to the clock signal? Example answer: It changes on the next falling edge of the clock that occurs after the D signal becomes a 0.

This circuit remembers input, but only observes that input when the clock signal changes from high to low. This means that it can simultaneously receive input for a new state, while sending output from its old state, and flip over from the old to the new in an instant. Try the following:

  1. Disconnect the input switch from the D input (you can just drag it to the side in the Falstad simulator or use the lightning tool in LogicWorks to remove the connection).
  2. Take the output Q2 and connect it to a NOT gate oriented back towards the start of the circuit.
  3. Connect the output of that NOT gate back to the D input of the first D latch, where you just disconnected the input switch.

Notice: if this were a D latch, by connecting the output back to the input via a NOT gate, you’d have an inconsistent circuit: as soon as you turned the clock on, the circuit would rapidly flip back and forth between on and off, and it would be difficult to predict the state it would end up in when you turned off the clock. However, this circuit is different. Describe what happens if you connect the output Q2 through a NOT gate back to the input D:

Example answer:

At each falling edge of the clock, the Q2 value changes to match the Q1 value, which has been storing the D input. This in turn flips the D input to the opposite of what it had been via the NOT gate. However, this does not create a contradiction, since with the clock off, the new D input does not affect Q1. At the next rising edge of the clock, the new D input gets forwarded to Q1, but still does not affect Q2, so the circuit is still consistent. Finally, at the second falling edge of the clock, the new Q1 value forwards to Q2, swapping the D input once more, and the cycle begins again. This circuit ends up creating an on/off pattern that consists of on pulses which are twice as long as the clock pulses it receives, always starting and ending on the falling edges of the input clock signal.

This simulator link shows what the circuit looks like with the NOT gate hooked up.

Register

A register is an n-bit memory (contains n flip-flops, which share a common clock, and are therefore all written to simultaneously). For example, the following diagram is an abstraction for a device that internally contains 16 D flip-flops, and can store 16 bits of information.

Note: the diagonal slash through a line indicates that the line represents multiple wires; for this example, 16. This is called a “bus” and when we separate the individual wires out of a bus, that’s called a “breakout.” LogicWorks allows you to create buses and breakouts, but the Falstad simulator does not. In the Falstad simulator, we will instead use banks of named nodes that we can copy and paste, since named nodes are considered connected to each other.

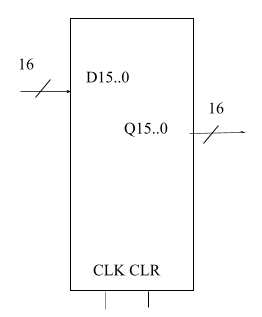
A logic diagram with inputs D0-D15 on the left, outputs Q0-Q15 on the right, and inputs CLK and CLR on the bottom. The D and Q inputs are not represented as individual wires, but instead as single wires where the wire part has a diagonal slash through it and the number 16 written above the slash. Inside the component, the inputs are simply labeled “D15..0” and “Q15..0” . 

You can do the following with this device:

  • You can read the current contents of the register at the outputs Q15..0
  • You can write a new value to all 16 bits at once by setting the value at the inputs D15..0, and then pulsing (setting to high, then back to low) the CLK input.
  • You can also clear all 16 bits to 0 at any time by activating the CLR input (when not using the CLR input, keep it set to 0).

Exercise 9:

For this exercise, either download this register circuit and open it in LogicWorks, or work in the frame below where we’ve set up a similar circuit in the Falstad simulator (or use the “Register” tab in the CircuitVerse project).

The inputs to the register should all be zeroes, but notice that the outputs are not all zeroes. How is this possible?

Example answer: The register stores data, and only updates when the clock input is pulsed. So although the inputs are zeroes, the stored data matches what is shown in the hex displays.

Now pulse the clock input (CLK in LogicWorks and Ld in Falstad) to forward through the inputs, setting the outputs to zeroes. Then, manipulate the circuit so that the output shows “C5F0” from top to bottom, and describe what you did:

Example answer: First, set the inputs to “C”, “5”, “F”, and “0”, which in binary becomes 1100, 0101, 1111, and 0000. Next, turn the clock on and off again, to trigger an update of the stored value.

Stretch Exercises: Register File

If you’re making up for Lake Day, skip these stretch exercises and skip ahead to Lab 5, Exercise 2 instead.

For this and subsequent parts of the lab, if you’re working in CircuitVerse you’ll need this hw_isa.cv project.

A register file is a set of registers that can be read from and written to. We number the registers in the set, and use the numbers to specify which registers from the set are accessed at any particular time.

Our register file has 16 registers, numbered 0 to 15 (note that it takes 4 bits to encode the register number).

Each register stores 16 bits of data (similar to the register from the previous exercise).

Registers 0 and 1 don’t store data like the others, instead they are always set to 0 (for register 0) and 1 (for register 1).

Below is an abstraction for a register file. You can read the data from each of 2 registers and write new data to a third register simultaneously.

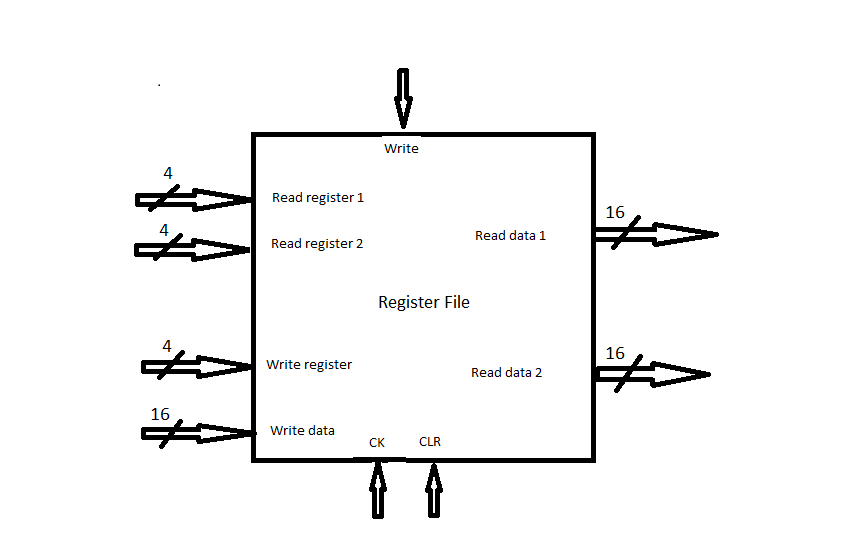
Logic diagram for a register file. It has a “Write” input at the top and “CLK” and “CLR” inputs at the bottom. It has four inputs on the left: 4 bytes of “Read register 1,” four bytes of “Read register 2,” four bites of “Write register,” and 16 bytes of “Write data.” Then it has two 16-bit outputs on the right: “Read data 1” and “Read data 2.” 

To read the contents of 2 registers at any given time, specify the number of the first register at the Read register 1 input, and the number of the second register on Read register 2.

The contents of the two registers are then available at the Read data 1 and Read data 2 outputs.

To write a new value to a specified register, set the Write register”” input to the number of the register, set the Write data** inputs to the value to be written to the register, and then pulse the Write line.

Exercise 10:

Download this regfile.cct circuit and then open it in LogicWorks (we don’t have a Falstad implementation this time, but you can use the “Register File” tab in CircuitVerse; see project link above).

The blue wires that split into many labeled ends are called “buses,” and the parts that split out are “breakouts.” You can use the heavy + tool to create buses, and you can right-click on a bus to create a breakout by entering the wire names you’d like to use. For example, entering “D0..15” will create a 16-wire breakout. Breakout ends with the same name only count as connected if there is a bus connecting the two breakouts.

To read the values currently stored in the registers, do the following:

  1. Set the Read register 1 and Read register 2 inputs to register numbers you wish to read from (start with 0 and 1).

  2. Examine the value stored at those registers at the outputs Read data 1 and Read data 2.

Write the value stored in each register from the table below. (Write values as upper-case 4-digit hex numbers, without any prefix). Remember you can read two at a time.

GCorrect answer:

  • Register 0: Correct answer: 0000
  • Register 1: Correct answer: 0001
  • Register 2: Correct answer: C5F0
  • Register 3: Correct answer: FEED

Correct answer: See above

To clear all the registers, set Write = 0 and pulse CLR (this input is controlled by a push-button, so click once to pulse). Do this now.

Next, follow these directions to write values to registers 4 and 5:

  • Set Write = 1.
  • For each register:
    • Set Write register to the number of the register to write to.
    • Set Write data to the data specified.
    • Pulse the CLK.
  • Set Write back to 0 to disable writes.
Register Data
4 FACE
5 ACED

After you have written these values specified, set the circuit to read registers 4 and 5. Confirm the following:

GCorrect answer:

  • Value of Read Register 1: Correct answer: 4
  • Value of Read Register 2: Correct answer: 5
  • Value of Read Data 1: Correct answer: FACE
  • Value of Read Data 2: Correct answer: ACED
  • Clock pulses required to write registers 4 an 5: Correct answer: 2

Correct answer: See above

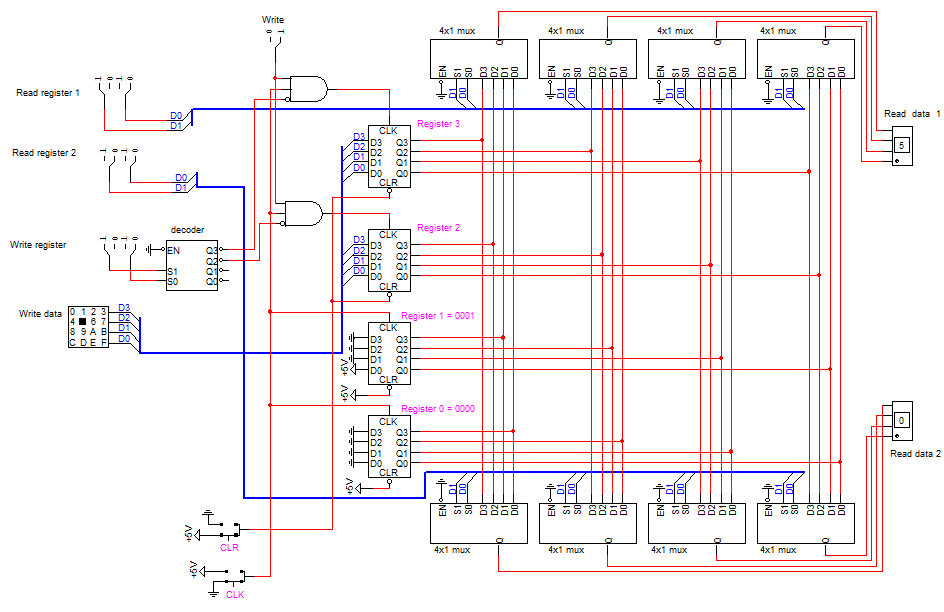
Below is LogicWorks circuit which implements a register file for a set of 4 4-bit registers. Register 0 always produces a value of 0, and register 1 always produces a value of 1 (those values are hardwired in this circuit).

This register file circuit is small enough that you can examine and understand the underlying circuitry:

A diagram of a 4-register 4-bit register file. It 2-bit inputs “Read register 1,” “Read register 2,” and “Write register” on the left. It also has a hex keyboard to specify a 4-bit “Write data” input. At the top it has a 1 bit “Write” input, and at the bottom it has push-buttons for pulsing “CLR” and/or “CLK” inputs. It has four 4-bit registers, as well as 8 4x1 muxes that connect in two groups of 4 to the “Read data 1” (on top) and “Read data 2” (on bottom) outputs. The internal connections are as follows: First, the “Read register 1” and “Read register 2” 2-bit values are connected to the S0 and S1 bits of the muxes. “Read register 1” connects to each of the 4 top muxes which together produce the 4 bits of “Read data 1” output, while “Read register 2” connects to the select bits for each of the four bottom muxes feeding “Read data 2.” Next, each output wire from each of the four registers outputs is hooked up to two muxes: Register 3 output 3 to the D3 input of the 3rd top and 3rd bottom mux, then Register 3 output 2 to the D3 input of the 2nd top and bottom muxes, likewise with outputs 1 and 0 to the second and first top and bottom muxes. This way, when the select bits read 3, all 4 bits of the 3rd register will be selected as the 4 bits to output, for either the top or the bottom output. The connections for the other 3 registers follow this pattern as well. As for the register inputs, the top two (registers 2 and 3) each receive a CLR input directly from the CLR button. The CLR input is permanently turned off for registers 0 and 1. Those two registers receive CLK input directly from the CLK button. But the top two registers receive CLK input from AND gates (more on those in a second). The inputs for registers 0 and 1 are hard wired: all ground for register 0, and D0 to +5V with the rest to ground for register 1. This ensures these two registers always hold values 0 and 1. The data input from the “Write data” hex keyboard is routed to both register 2 and register 3. The “Write register” input, meanwhile, goes into a 2x4 decoder, with outputs Q0 through Q3. Outputs Q0 and Q1 are disconnected (because writing to those registers is not allowed) but outputs Q2 and Q3 connect to one input each of two 3-input AND gates. These are the AND gates that drive the CLK signals for registers 2 and 3, mentioned before. Their other inputs are the CLK button, and the “Write” input. This means that for a particular register to receive clock input, three things have to be true: It has to be the register selected by the “Write register” bits, the global “Write” line has to be active, and the CLK button has to be pushed. There are a few active-low lines that have not been specified in this description to reduce its complexity, and the muxes all have enable inputs that are permanently activated. 

Exercise 11:

What is the purpose of the decoder device in the circuit?

Example answer: It turns a binary number specifying which register to write into a 1-hot encoding so that the clock for the indicated register can be turned on when the CLK button is pushed while all other clocks are left off.

Explain how the multiplexers are used to produce the value of the specified registers at the Read data 1 and Read data 2 outputs:

Example answer: Four multiplexers are used for each read output, each taking one signal from each register. Each multiplexer handles the output for a particular bit (so e.g., it reads bit 0 of each of the 4 registers and writes bit 0 of the read output). The multiplexers all receive the same select inputs (from the read register 1 or read register 2 input, depending on which output they’re for). This means that all 4 bits of e.g., register 2 will be sent to the read data 1 output when 2 is selected in binary as the read register 1 input.

Extra exercises: RAM Memory

This exercise will show you how a RAM device is used to store and retrieve values from memory.

Download this instructionMemory.cct circuit and then open it in LogicWorks (or go to the “RAM Test” tab in CircuitVerse):

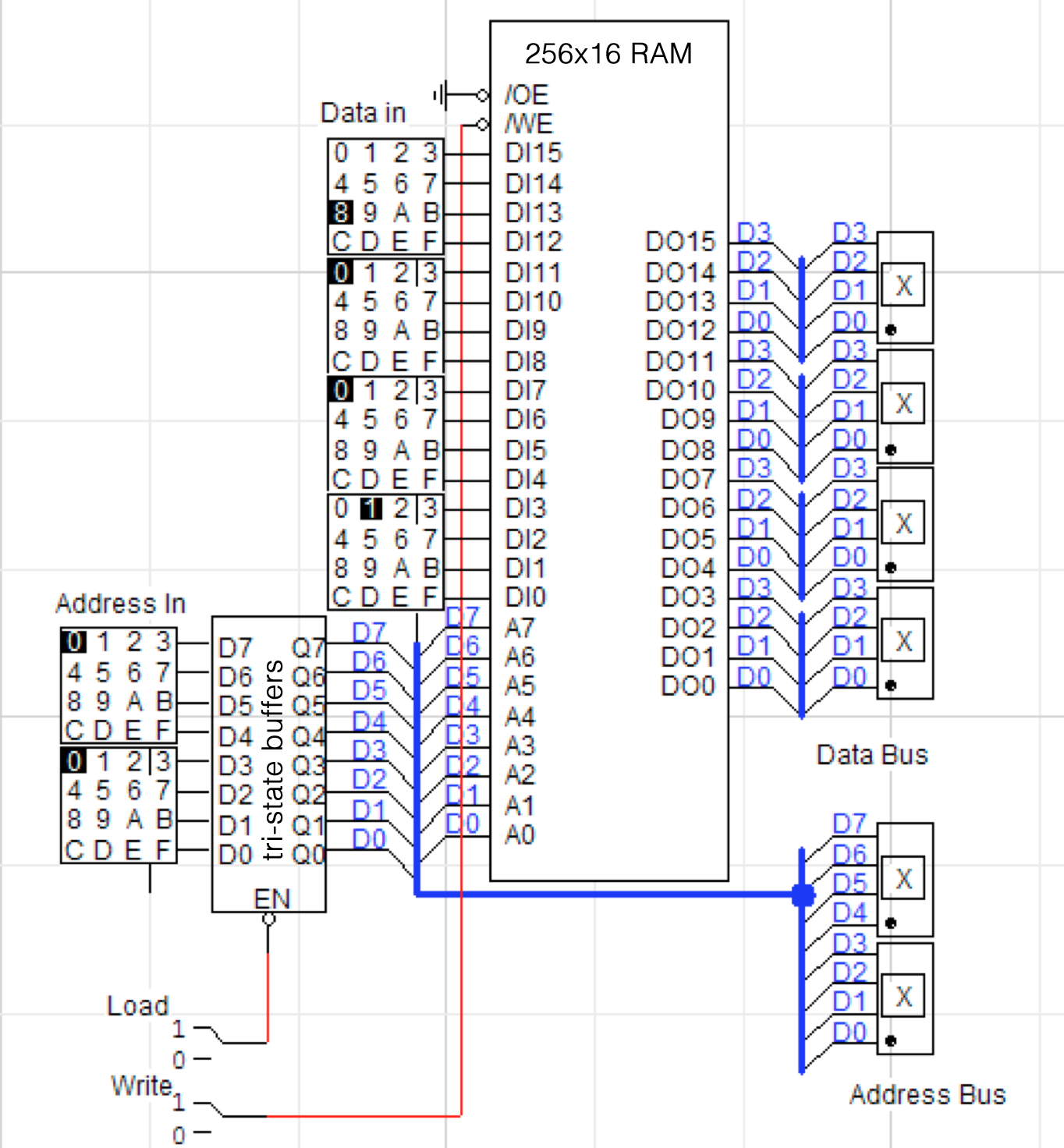
Logic diagram for instruction memory. On the left, it has two hex keyboards to specify an 8-bit Address in value, which is fed into an 8-input/8-output tri-state buffer. The enable line of this buffer is connected to a binary switch labeled “Load.” A second “Write” switch is below that, and connects further on to the write-enable input of a “256x16 RAM” component. Both the tri-state buffer enable input and the write enable of the RAM are active-low. The 8 tri-state buffer outputs holding the address connect to the A0-A7 inputs of the RAM, and are also forwarded to two hex displays labeled “Address bus.” Their values are both ‘X’ in the image, because the tri-state buffer is not enabled (“Load” is set to 1). The RAM has 16 data inputs which are connected to 4 hex keyboards labeled “Data in.” It also has an “/OE” input which is active-low and connected to ground (so always activated). This is for disabling the output, which we don’t need to do here. The RAM has 16 outputs, DO0 through D015. These are connected to a bus labeled “Data bus” and thence to four hex displays (which each read ‘X’ in the image). 

This circuit can be used to store data into addresses of a RAM memory, which is necessary for loading a program into the instruction memory.

Examine the circuit carefully to understand its operation: you write data values into a memory location specified by an address by using the hex keyboards on the left to specify the data and address.

The currently selected address and the value stored at that address are displayed on the hex displays on the right.

Exercise 12:

To read from memory: 1. Set Load to 0 (the Load line connects the address switches to the memory chip through the tri-state buffers, which let a signal through only when Load is set to 0. When inactive, the tri-state buffers have neither high nor low output, which LogicWorks shows as an ‘X’). 2. Select the address you want to read from on the Address in keyboards. 3. The data at that address will appear on the Data bus at the right.

Read the data at addresses 0 through 3, and confirm it below (enter just the 4 hex digits you see, from top to bottom):

GCorrect answer:

Address 00: Correct answer: 5002

Address 01: Correct answer: 5003

Address 02: Correct answer: 5003

Address 03: Correct answer: 0230

Correct answer: See above

Exercise 13:

To write to memory (load a program): 1. Set Load to 0. 2. Set the Address switches to the location in memory at which you wish to write a data value. 3. Set the Data switches to the value you wish to write to that location. 4. Set Write to 0, then back to 1 (writes the data input into the specified address in memory). 5. Repeat steps 2 - 4 for each address and its data value.

Using the write procedure, load the following data values to the specified addresses:

Addr Data
00 5002
02 5003
04 1220
06 0230
08 2122
0A 8001

As you write the values, you will observe the address and data values on the data and address bus displays. At any time, you can observe the contents of an address by setting the address switches to the desired location (without toggling the Write switch).

When you are finished, set Load = 1 to disable the address inputs.

This will always be required when the user is finished loading the program into memory, and wishes to run the program. When RAM is used as part of a full computer, the address is supplied by the CPU during execution of the program, so the switches are not needed at that point (and would interfere with the CPU operation if still connected).

Given that the RAM has 8 address inputs, how many storage slots does it have (i.e., how many distinct addresses are there)? Correct answer: 256

Which part(s) of this RAM would it make sense to hook up to which part(s) of an ALU in a design for a full computer (there are several good answers here)?

Example answer: The “Data in” could be hooked up to an ALU’s result to store that result in memory. Similarly, the “Data bus” outputs could be hooked up to one of the inputs of an ALU in order to use data from memory as part of an operation. Although less obvious, the address bus could serve as input and/or output as well, if we need to compute the address of some data using a formula. For example, using the address as one input and the number 1 as another input and setting the ALU to do addition, we could compute the next higher address as part of a solution for writing multiple values into sequential addresses. Finally, one could hook part of the data bus outputs into the Operation bits of the ALU, to let the data determine what operation the ALU will perform!

Extra exercises: Underlying Memory Organization

The circuit below shows how a larger memory is organized from basic latches. Examine the circuit carefully:

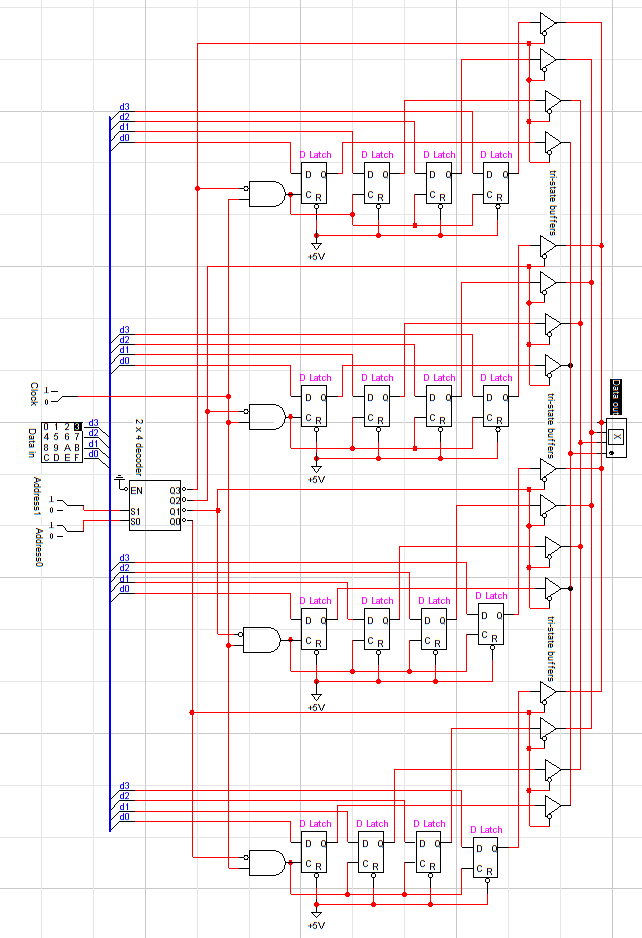
A circuit diagram. On the left, there’s a “Clock” input switch, four “Data in” inputs connected to a hex keyboard, and two “Address” input switches. On the right, there are 4 bits of “Data out” connected to a hex display. The address inputs go into a 2x4 decoder, resulting in address lines Q0 through Q3. These feed into four AND gates along with the Clock signal, so that according to the current address, when the clock is on, only one of the four AND gates will be active. Each AND gate is connected to the C input for four different D latches, which receive their D inputs from “Data in” inputs D0-D3 respectively. These latches have their R input permanently deactivated, and their Q outputs connect to one of four tri-state buffers, which are enabled by the same address Q line that enables the AND gate for that set of latches. The four groups of four tri-state buffers are interleaved and connected to the four “Data out” lines: the top buffers from each group connect together at the top output of the “Data out,” and likewise with the third, second, and first outputs. Thus each output line is connected to 4 different tri-state buffers: one from each of the four groups of buffers corresponding to the four groups of latches. Of the four tri-state buffers connected to each output, each comes from a different group, and thus would be enabled by a different address line. 

The triangular symbols are tri-state buffers, which act to either allow connection between the input and output of the gate (when enabled), or disconnect (when disabled). The enable line for the tri-state buffers is active low.

Exercise 14:

Describe the overall purpose of this circuit.

Example answer: This circuit allows you to read and write memory and also select where to do so, it’s a random access memory or RAM circuit. At all times, based on the 2 address bits, one of the four sets of tri-state buffers is active, sending the (4-bit) contents of memory at that address to the output. If you want to overwrite memory at the currently selected address, just turn the clock on and the clock inputs of the D latches for that address will be activated, allowing the 4 bits of “Data in” to replace the old data at that address (and the output will be updated immediately as well).

How is the 2x4 decoder used?

Example answer: It turns a 2-bit binary address into a 1-of-four-lines-is-on signal to send enabling signals to just one of the four memory units at once, and similarly to enable one of the four sets of tri-state buffers.

What is the purpose of the tri-state buffers?

Example answer: When not enabled, they prevent different memory outputs from sending signals onto the same wire, which could result in a short circuit. When one set of the 4 is enabled, it forwards the signals from the 4 bits of the associated register to the output lines.