CS 240 Lab 2: Data as Bits
Peter Mawhorter
How do Computers Work?
When you press the power button, electricity flows through a bunch of transistors. This feeds power to things like a keyboard & monitor, which send inputs into or receive outputs from the transistors.
The transistors are organized into logic gates, like AND and OR.
But what about… ?
- There are tens of billions of transistors in a modern computer. How are they connected?
- Transistors have 1 input & 1 output. How do we represent numbers or text?
- Logic gates just compute a single outcome from some inputs. How do computers deal with signals over time? How is memory implemented?
- How can we change what a computer does by writing a program, instead of having to re-wire it?
Outline
- Memes & Questions
- Representing Numbers
- Counting with a Circuit
- BREAK
- Designing Circuits
- Bit Puzzles
Memes & Questions
Setup status?
- Has everyone successfully run
cs240 auth -i s23? - Questions about
cs240script orgit?
Representing Numbers
Representing Numbers
- Binary represents numbers using 0 and 1
- In base 10, each digit represents
- 1, 10, 100, 1000, etc.
- In base 2 (binary), each digit represents
- 1, 2, 4, 8, 16, 32, 64, 256, 512, 1024, etc.
- We call these digits “bits”
- These numbers show up everywhere in CS
- In base 10, each digit represents
- We use a suffix when base is unclear:
- For example,
Converting to Binary
- Figure out biggest power-of-2 that’s smaller
- Hint: 1024 is
- This is the largest bit that’s a 1
- Repeat with the remainder after subtraction
Hexadecimal
- Binary numbers are long and hard to read
- Decimal numbers are hard to convert to/from binary
- Hexadecimal is a compromise: base-16
- Because the base is a power-of-2, conversion to/from binary is easy
- Large enough to be short
- Close enough to base-10 to be somewhat intuitive
Hexadecimal
- Uses letters A-F in addition to numbers 0-9
- Each digit is , and converts to/from 4 bits
- A
0xprefix is often used, e.g.,0xF83A - Two hex digits are 8 bits, which is a byte
- Bytes are a common unit of information because one byte is enough to represent any letter of the Latin alphabet + plenty of symbols (see ASCII)
- Max value of a byte is 255, which is
FFin hex
- Converting to binary: convert each digit + concatenate
Two’s Complement
How to represent negative numbers using bits?
- Could use one bit to represent +/-, and leave other bits alone
- 4 bits would represent -7 () to +7 (), including +0 () and -0 ()
- Adding two negative numbers requires special logic
- Instead, let the first bit represent
and then other bits add to that to bring us closer to 0.
- Now 4 bits can represent -8 () to +7 (), with just one 0 (). -1 is represented as -8 + 7 = .
Advantages of Two’s Complement
- Only one zero (simplifies equality checking)
- Addition & subtraction work using a single algorithm for
positive and negative numbers
- When adding a positive number to a negative number, the overflow into the sign bit will correctly determine whether the result is positive or negative
- See this StackOverflow answer for more.
Counting w/ a Circuit
Logic Diagrams
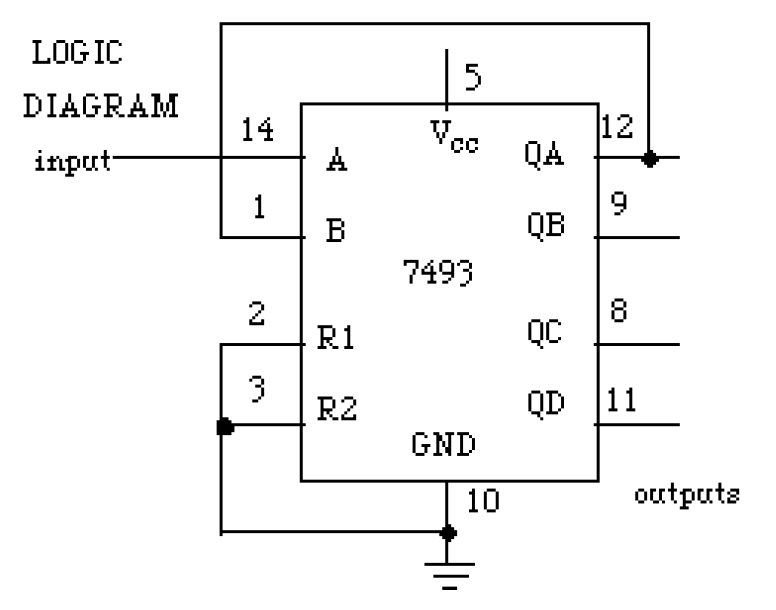
- NOT the same as a pinout.
- Inputs on the left
- Outputs on the right
- Voltage on top
- Ground on bottom
Logic Diagrams
- The layout inside a chip is set up to minimize fabrication costs, not to make your life easy.
- When wiring things on the protoboard, ignore the logic diagram layout and just pay attention to the pin numbers.
At this point, complete exercise 1 in the notebook by wiring the 7493 up to a push button plus logic outputs and observing its behavior.
Now, add wires to connect your 7493 to the TIL311, and complete exercise 2 in the notebook.
Timing Diagrams
-
Combinational logic circuits can be represented by a
truth table or an expression in Boolean algebra.
- They have 1-way paths from inputs, through gates, to outputs: no loops.
- Is the 7493 a combinational circuit? NO
-
But what about memory and changes over time?
- We’ll need more complex notation
- Sequential circuits have internal state
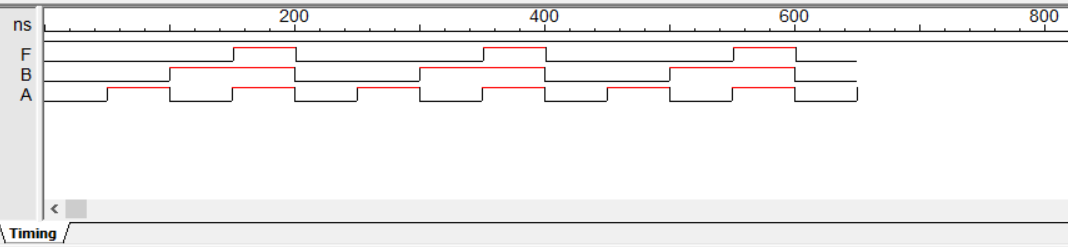
Timing Diagrams
- A Timing Diagram shows the high/low state of
multiple inputs/outputs as they change over time
- Plots time on the X-axis vs. voltage on the Y-axis
- Each input or output has its own stacked Y-axis
What combinational function is this?
Timing Diagrams
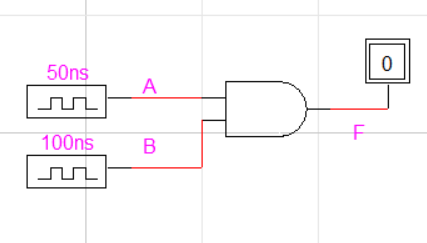
- Inputs are clocks:
- Off for ns then on for ns
- Editable via the “Delay.Dev” attribute in LogicWorks

Timing Diagrams
- Sequential circuits have behavior that changes over
time
- Some elements may trigger based on a change in voltage, rather than a particular stable voltage
- System state may depend on hidden internal variables
- Timing diagram shows how inputs/outputs change over time, but it doesn’t show hidden variables directly
- We’ll see more of these later
Now, open LogicWorks and work through Exercise 3 in the notebook.
BREAK
Designing Circuits
Designing Circuits
- Given a truth table, how to design a circuit for it?
- Use sum-of-products to build a Boolean expression
- Wire up gates for each operation
- Might be an inefficient circuit if you don’t simplify
- Gets messy w/ many inputs
Designing Circuits
- Can also use intuition, especially when building for many inputs
- Often, we have 8, 16, or 32 bits (= wires) to work with
- Just like trying integration rules in calculus, you can try out different operations over many bits mentally, and work towards a solution
Parity
- A parity bit is set so that the total number of ON bits in a message, including the parity bit, is even
- By sending a parity bit along with each row of a message, you can quickly determine if a row of the message has been corrupted (assuming only 1 bit is corrupted)
- Using row & column parity bits, you can often localize & correct errors
has 3 bits set, so the parity bit would 1
has 2 bits set, so the parity bit would 0
Parity with XOR
- It’s possible to design a circuit for the parity bit of a message using only XOR gates.
- The truth table for parity P on 2 bits A and B is the same as XOR.
- How to do this for more bits?
| A | B | P |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Work through Exercise 4 in the notebook in LogicWorks.
Bit Puzzles
Bit Puzzle Goals
- Exercise + grow your intuition about logical operators
- Learn some tricks that may eventually come in handy
- Gain a thorough understanding of 2’s-complement representation
Bit Puzzle Tips
- Work with 4-bit or 8-bit values; double-check with 32 bits
- Write out (by hand can be good) results from applying a few operators to see if you can see a pattern
Things to try:
- Complement the number
- Add or subtract 1
- Mask (
&with a mask value like0x0F) - !(0) = 1, but !(any other number) = 0
- Use XOR to compare values
- Bitwise OR a general solution with a special case
- Shift left & then right (or vice versa)
Work on Exercises 5-7 in the notebook as practice for the upcoming Bits assignment.