▲ ☰ ▼

CS 240 Lab 3

Data as Bits

CS 240 Lab 3

Arithmetic Circuits

All the circuits you will work with today in lab are combinational circuits. Like basic gates, the output of combinational circuits depends only on the current inputs to the circuit. Combinational circuits are made with basic gates, but produce more complex functions.

Certain functions are very useful for a variety of tasks that help us design important components of a computer, so we examine them here. These include the multiplexer, decoder, demultiplexer, encoder, and the adder (the basic arithmetic circuit for addition).

Multiplexer

Exercise 1:

Although you may not have realized it, in the first problem on the lab assignment, you designed a simple 2x1 multiplexer (MUX), which you have also learned about in lecture.

A multiplexer can be thought of as a steering circuit, which steers a single input from a set of inputs through to the output, based on the select line.

A diagram showing a mutiplexer as multiple wires that come in, one of which is connected to the output wire, with the select inputs controlling which connection is made. This isn’t actually how it’s implemented using transistors, but it’s a good analogy.

A schematic diagram showing conceptually how an 8x1 mux works.

The symbol for a multiplexer: a trapezoid with the narrow end facing right, which is where the output (Q) comes out. The inputs (D0 and D1) come into the wide end on the left and the select input (S) comes into either the top or the bottom (the bottom in this image).

The logic diagram symbol for a 2x1 mux.

A trapezoid with the wide end towards the left, where there are 8 wires coming in labeled 0 through 7. There’s one wire going out the right side, and another connection at the bottom. The wires on the left and right are light or dark green indicating a single wire. The connection at the bottom is black, which hints that it’s actually a 3-wire bus, not a single wire.

An 8x1 MUX has 8 input lines on the left, 3 select lines (in CircuitVerse, a single 3-wire bus at the bottom), and 1 output line on the right.

Use this link to open CircuitVerse, and then download & import this circuit project. If it stalls during loading check this lab 2 footnote. The project file contains all of the circuits you’ll need for this lab in different tabs, including blank tabs for circuits you should build yourself.

Open the “8x1 Mux” tab and follow these steps:

From the “Decoders and Plexers” section the “Circuit Elements” panel, select a “Multiplexer” and add it to your circuit.
Select the multiplexer, and in the “Properties” panel, set the “Control Signal Size” to 3. The size should increase and there should now be 8 inputs instead of just 2.
Connect the 8 D0-D7 inputs that are already set up to the 8 inputs on the left side of the multiplexer.
Connect the output of the multiplexer to the Q output.
Connect the 0:2 wires that are split off from the “Keyboard Hexer” upwards to the select input of the multiplexer (one line in the simulator will hold all 3 wires at once).

But how can you hook up 3 wires with just one line?

In the “8x1 Mux” tab in CircuitVerse, when we insert the 8x1 multiplexer, it only has 1 connection on the bottom, but we need 3 bits to select one of 8 inputs. As it turns out, CircuitVerse has the ability to use lines in a circuit diagram to represent a bundle of wires instead of just a single wire. Instead of light or dark green to indicate high or low voltage, a bundle of wires will just show up as black. These are created automatically when connecting from or to multi-bit inputs/outputs. For example, at the bottom of the circuit template there’s a “Keyboard Hexer” and the right-side output from that is a 4-wire bundle (because a hex digit is represented using 4 bits).

The circuit actually splits up the 4 bits from the hex digit into one group of 3 plus a leftover bit that we leave disconnected. That’s called a “breakout” (or a “splitter” in CircuitVerse terminology). This diagram shows how a breakout circuit symbol would actually work in terms of wires:

The breakout symbol shows one wire bundle coming in and splitting up into one or more groups, with the numbers indicating which wire(s) go in which group(s). In a physical circuit, you’d have multiple insulated wires bundled together and then some of them would split off into a different bundle. We count wires that represent numbers starting from the least-significant bit of a binary number as ‘0’. So if we took the hexadecimal digit 9 (1001 in binary) and split it into “0:1”, “2”, and “3” groups, the “0:1” group would be binary 01 (the two least-significant bits), the “2” group would be a 0, and the “3” group would be a 1.

If we split 4 wires into “0:2” and “3” groups, and the 4 wires had bit pattern 1101 for the number 13 (hex digit D), what bits would the first group have in it?

Correct answer: 101 Explanation: The first group takes the 3 least-significant bits, so the 1s, 2s, and 4s places. The other wire split off would be a 1.

Now that things are hooked up, you can click on the keyboard input and type in a hex digit to set the values of the select lines. Answer these questions:

Which hex digit should you use to set the select lines to S0 = 0, S1 = 1, and S2 = 1?

Correct answer: 6 Feedback: This would also work, since E is 1110, and the 4th bit is discarded. Feedback: We expected just ‘6’ but this is correct. Explanation: 6 is 0110 and E is 1110, so either will work since we discard the 4th bit.
Set the select lines to S0 = 0, S1 = 1, and S2 = 1 by entering the hex digit you just identified on the keyboard input (click to select it then type the digit on your keyboard). With this select configuration, which of the 8 data input(s) affects the output (toggle them to test)?

Example answer: Only input number 6 will affect the output.
Now set the select lines to S0 = 1, S1 = 0, and S2 = 0 (enter ‘1’ on the keyboard). Does the same input still affect the output? yes
no

Which input(s) will affect the output now?

Example answer: Now only input number 1 affects the output.
What is the relationship between the data inputs, the select inputs, and the output of a multiplexer?

Example answer: The select bits are interpreted as a binary number. This specifies which of the data inputs should be forwarded through to the output. The other data inputs are ignored. That’s why there are always $2^n$ data inputs for $n$ select bits.

Exercise 2:

The “4x1 Mux Gates” tab in CircuitVerse has an implementation of a 4x1 multiplexer using basic gates.

Edit the circuit by removing components to create a 2x1 multiplexer. Verify that it works by manipulating your inputs and observing the output, and then describe your circuit below:

Example answer:

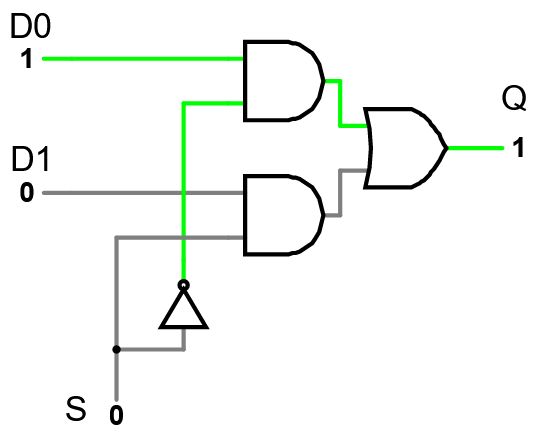
A 2x1 multiplexer circuit diagram, showing how it’s implemented (see description below)

Two inputs each connect to a separate AND gate. The other inputs of those and gates connect to the single selector input, with a NOT gate on one of them. This means that switching the selector back and forth switches which AND gate gets activated by the selector input, but only one of them does at a time. Both AND gates connect to an OR gate whose output is the circuit output.

You can cross-check your design with the “2x1 Mux Gates” tab.

How many different input combinations should you test to thoroughly test the circuit? Correct answer: 8 Explanation: Since there are 3 inputs (2 data inputs and 1 select input) we have $2^3 = 8$ possible input combinations to test.

Exercise 3:

A multiplexer can be used to implement any boolean function by hard-wiring the data inputs to fixed high or low values. The select lines become the inputs to the boolean function, and based on the desired truth table, you set the appropriate data input to either 0 or 1.

This following truth table for a function Q indicates whether or not a 3-bit value S2 S1 S0 is a power of two:

S2	S1	S0	Q
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	0

Here is a pin-out for a 74151 8x1 multiplexer:

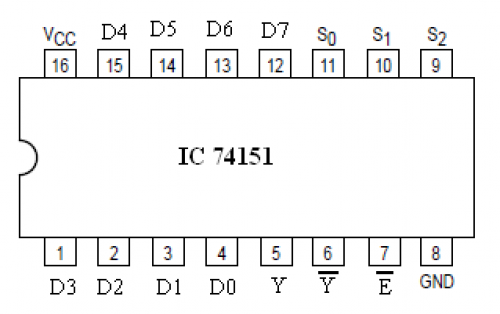
Pinout for the 74151. The notch is on the left, with pin 1 below it and pins numbered counterclockwise around the chip. There are 8 pins on each side. In order, the pins are labeled: D3, D2, D1, D0, Y, Y-bar, E-bar, GND (pin 8), S₂, S₁, S₀, D7, D6, D5, D4, and Vcc (pin 16).

On your protoboard, there is a 74151 chip (8 x 1 MUX) inserted in the top-right area. Connect it to produce the function Q (answer some of the questions below to help figure out how).

Output is measured at Y (pin 5). It is not necessary to use or connect pin 6.

Don’t forget the power (pin 16), ground (pin 8), and enable line (pin 7, connect to ground)!

The enable line (pin 7) is called active low. In the pinout diagram, it has a bar above an E, where the bar is the same notation used for NOT in boolean logic (sometimes you’ll see a little circle on the corresponding leg of the chip for a NOT gate instead). Inputs and outputs that are active low are active when voltage is low, rather than high like most other inputs/outputs. So to enable this chip, you must connect pin 7 to ground (low voltage)

When everything is plugged in, how many logic switches should be connected?

0
1
3
8

Which inputs should those switches connect to? Example answer: They need to connect to the S0, S1, and S2 inputs, which are pins 11, 10, and 9.

Where should the data inputs D0-D7 be connected? Example answer: Each data input should connect to either the +5V or ground rail via a wire. For this circuit, D1, D2, and D4 should connect to +5V and the rest should connect to ground.

Confused? Click here for hints.

The key to this exercise is to figure out what “hard-wiring the data inputs” means. The data inputs are D0-D7. Rather than connect these to switches, like you did in the previous exercise in the simulator, you’re going to connect each one directly to either +5V or ground, to establish a permanent high or low voltage signal for that input.

The goal given that info is to figure out: which data inputs should I connect to +5V and which should I connect to ground, in order to make the chip behave according to the specified truth table?

You will connect S0/S1/S2 to three of the logic switches, because those inputs are what you’ll be manipulating.

Demonstrate to the instructor that your circuit detects inputs on the select lines which represent a power of 2.

Decoder

Exercise 4:

A $n \times 2^n$ decoder has $n$ inputs and $2^n$ outputs. Only one of the outputs is active for any given $n$ -bit input combination.

In the second problem on the pre-lab assignment, you designed a simple 2x4 decoder. Assuming 2 inputs D0 and D1 and 4 outputs Q0 - Q3, and:

Q0 is only true when D1D0 = 00 Q1 is only true when D1D0 = 01 Q2 is only true when D1D0 = 10 Q3 is only true when D1D0 = 11

This can be described by the following truth table:

D1	D0	Q0	Q1	Q2	Q3
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

Such a device is said to decode the binary number which is specified by the inputs, activating the output which corresponds to the decimal value of the binary input.

On the pre-lab, you should have designed a circuit that looks something like this:

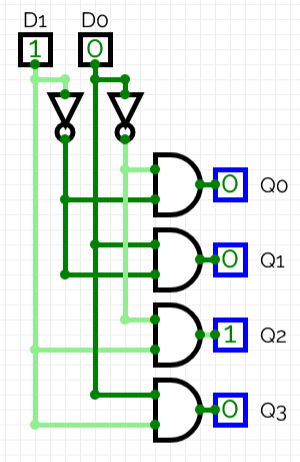
A circuit diagram with inputs D1 and D0 at the top. It has 4 AND gates feeding into outputs Q0 through Q1 on the right. Wires distribute normal and inverted versions of D0 and D1 to the AND gates as follows: Q0 is NOT-D1 and NOT-D0, Q1 is NOT-D1 and D0, Q2 is D1 and NOT-D0, and Q3 is D1 and D0. In the diagram, D0 is off and D1 is on, activating the Q2 output and leaving the rest inactive.

Build the circuit for the 2x4 decoder in CircuitVerse using the “2x4 Decoder” tab (it should be blank at first).

Notes on building the decoder:

You’ll have to add inputs and outputs. These will show up in the “Decoder test” tab as you add them.
You’ll find the gates you need in the “Gates” tab of the “Circuit Elements” panel.
Use the “Properties” pane to add labels to each input & output so you can tell which is which. Label your inputs D1 and D0 and your outputs Q0 through Q3.

When you set both inputs to 1, which of the outputs is/are active?

D0
D1
D2
D3

When you set both inputs to 0, which of the outputs is/are active?

D0
D1
D2
D3

Why doesn’t a decoder ever have more than one of its outputs active?

Example answer: The purpose of a decoder is to use $2^n$ outputs to indicate the binary value represented by a bit pattern on its $n$ inputs. Since any possible input pattern corresponds to a unique number, only the output line for that number will be active. Having two output lines active doesn’t make sense, because it implies that two distinct bit patterns are active at once, which is impossible.

Open the “Decoder test” tab in CircuitVerse. This is set up to test both your decoder implementation and the solution. The big chips in the middle are custom “tester” chips that read test inputs and expected outputs from a memory bank and then light up the “Wrong” light if a particular input doesn’t match the associated output (the “Failed” light lights up when the “Wrong” light does and stays on until the chip is reset). To use them, you can:

Hook up as many of the T0-T3 outputs as you need to the inputs of the chip being tested.
Hook up as many of the R0-R3 inputs as you need to the outputs of the chip being tested.
Connect a “Read-Only Memory” (ROM) chip from the “Sequential Elements” section of the “Circuit Elements” panel to the Taddr and Test lines at the bottom.
Enter values into the ROM by clicking on individual squares in the grid and typing them in. Each 2-digit value (8 bits) is split into 4 bits of “test input” and 4 bits of “expected output.”
Toggle the “RST” line on and then off again to reset the tester.
Each time you toggle the clock, it will switch to the next test stored in the ROM. When a test fails, it will light up the wrong/failed lights (and keep the failed light on until reset). Keep toggling the “CLK” input until you’ve run all the tests you want to.

During testing, the digits on the face of the chip will show the current inputs being sent to your chip, the current result from your chip, the expected result for those inputs, and which bit(s) have errors (each digit displays only a single bit).

We’ve done steps 3-4 above already. You just need to do steps 1 and 2, and then 5 and 6.

Demonstrate correct operation of the test setup to the instructor.

Exercise 5:

The 74138 is a 3x8 decoder chip. You will find one inserted in the bottom-right corner of your protoboard. Below is a pin-out for the 74138:

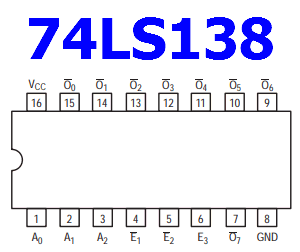
Make the following connections to the device:

Connect VCC pin to voltage and GND pin to ground on the board.
Connect the select lines A₀ A₁ A₂ on the chip to 3 Logic Switches on the board.
Connect each of the 8 outputs (O) on the chip to Logic Indicators on the board.
Connect the enable lines E₁ and E₂ to ground on the board.
Connect the enable line E₃ to voltage on the board.

Now complete this truth table based on your observations of the decoder:

GCorrect answer:

C	B	A
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

Correct answer: See above

The outputs for this device are active low. Describe what that means in your own words:

Example answer: It means that instead of high-voltage meaning ‘active’ while low voltage means ‘inactive,’ the opposite is true: low-voltage means ‘active’ and high-voltage means ‘inactive.’

Demultiplexer

A demultiplexer is the exact opposite of the multiplexer.

The symbol for a 1x4 demux: input D comes in on the left which is the short end of a trapezoid. Select inputs S0 and S1 come in from the bottom, and outputs Q0 through Q3 go out from the right (the wide end of the trapezoid).

The demultiplexer takes one single input data line and then switches it to only one of the individual output lines at a time based on selector inputs, leaving the rest of the output lines low.

Exercise 6:

Complete the truth table for the 1x4 demultiplexer with select lines S1 and S0 and input D.

GCorrect answer:

S1	S0	D
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

Correct answer: See above

Why are there some rows in the table where all of the data outputs are zeroes?

Example answer: Because if the input is 0, it doesn’t matter where it gets directed to, that line will be a 0 and the others will be zeroes by default.

Complete the Boolean algebra function for each output:

Q3 = Example answer: S1S0D

Q2 = Example answer: S1S0’D

Q1 = Example answer: S1’S0D

Q0 = Example answer: S1’S0’D

Exercise 7:

We can use the 74138 chip as a demultiplexer by hooking up our data input to the enable pin, so that when the ‘data’ is a 1 we get an output on the corresponding output line, and when the ‘data’ is a 0, we get no active outputs at all (because the chip is inactive).

Disconnect the E₃ enable line from voltage, and connect it instead to a push-button on the board.

If we set the select lines A₀, A₁, and A₂ to 1, 0, and 1 respectively, what number does that represent in decimal? Correct answer: 5

When the select lines are set that way, what will happen when we push the button?

Example answer: The 6th LED (index 5 counting from 0) should blink off as long as the button is pressed, and turn on again (so that they’re all on) when the button is released.

What configuration of select lines + the button state would cause the 4th LED (index 3 counting from 0) to turn off?

Example answer: Setting A₀ and A₁ to 1 and A₂ to 0, and then pushing the button should turn off the 4th LED.

Encoder

An encoder is the exact opposite of the decoder.

A schematic of a 4x2 encoder, which is just a rectangle with four inputs D0-D3 on the left and two outputs Q0 and Q1 on the right.

It takes $2n$ inputs (it is assumed that only 1 of the inputs can be active at a time). The input number of the input that’s active specifies a decimal number, which gets translated to binary on the output lines.

Exercise 8:

Complete the (partial) truth table for the 4x2 encoder:

GCorrect answer:

D3	D2	D1	D0
0	0	0	1
0	0	1	0
0	1	0	0
1	0	0	0

Correct answer: See above

Why doesn’t this truth table need 16 rows for 4 inputs?

Example answer: It doesn’t include rows which violate the assumption that only one of the 4 inputs is on at once. Since an encoder is supposed to take a “1-hot” encoding where only one wire is on and translate that to binary, its behavior is undefined when more than one input is on at once. There are multiple ways to build the circuit, which would have different behaviors for the rows not shown in the truth table above, but in theory, if people use the chip properly and only ever give it inputs where one wire is on, they shouldn’t matter.

Complete the Boolean algebra function for each output:

Q1 = Example answer: D3 + D2

Q0 = Example answer: D1 + D3

Why doesn’t D0 appear in either equation above?

Example answer: Because when D0 is the input that’s on, the correct output is 00, and so neither output variable is true. Boolean algebra formulas express what’s necessary to make something true, and they are false under any other condition.

Addition

In the pre-lab assignment for today, you saw that you can represent the sum of two single bit numbers A and B with the following truth table:

A	B	CarryOut	Sum
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

This points to the following logical formulae:

CarryOut = A AND B

Sum = A XOR B

Exercise 9:

Using the “Half Adder” tab of the CircuitVerse project, build the circuit which produces Sum and CarryOut from inputs A and B. You should use exactly one AND gate and one XOR gate.

Check your circuit against the truth table above. In particular, if you set both A and B inputs to 1, then:

GCorrect answer: CarryOut = 0
1

and Sum = 0
1
Correct answer: See above.

The following is the truth table for a full adder (which incorporates a carry-in bit to the sum of A and B):

CarryIn	A	B	CarryOut	Sum
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

The circuit for the full adder is:

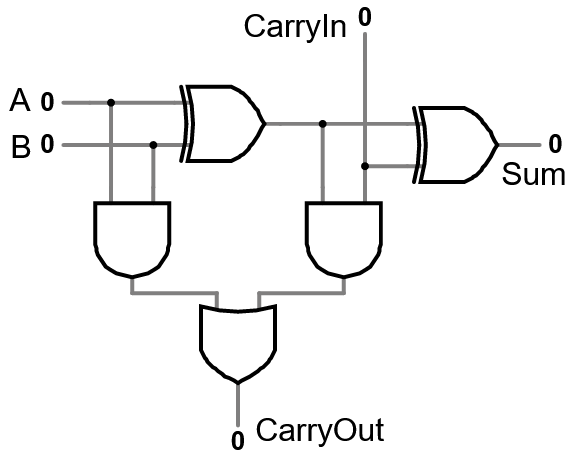
Exercise 10:

In the “Full adder” tab of CircuitVerse, build a full adder.

Go to the “Adder test” tab and cycle through the test cases to make sure it works (yours in on the left, solution is on the right).

Demonstrate its operation to the instructor.

Stretch Material: IC 7483

Note: You can disconnect the wires you have currently set up before working on this part.

You will find an IC 7483 inserted in the middle section of your protoboard. Here is a logic diagram of the chip (as usual, actual pins are numbered counterclockwise around the chip from 1 at the top left), along with a diagram showing the ordering for the input connections:

Logic diagram for a 7483. It shows 9 inputs along the left-hand side: B4 at pin 16, A4 at pin 1, B3 at pin 4, A3 at pin 3, B2 at pin 7, A2 at pin 8, B1 at pin 11, A1 at pin 10, and C0 at pin 13. Vcc (pin 5) is on top and GNC (pin 12) is at the bottom. The 5 outputs along the right-hand side are: C4 on pin 14, S4 on pin 15, S3 on pin 2, S2 on pin 6, and S1 on pin 9.

Logic diagram (NOT a pinout) for the 7483.

How to connect the inputs (output connections not shown). Ordering and grouping of A and B inputs is important.

Exercise 11:

Wire up the chip, following these guidelines:

Use logic switches on the board for the A and B inputs, and the PB1 switch for C0.
It is best to group the A switches next to one another (don’t alternate with the B switches), and arrange the input switches so the most significant bit is on the left (see diagram on the right).
Connect all 5 outputs to logic indicators, in order with S1 on the right, S2 to its left, etc. Leave a gap between S4 and C4 for clarity.
Don’t forget to connect Vcc and GND.

REMEMBER: the actual chip layout has pin 1 on the upper left, with 8 pins on each side of the chip numbered counterclockwise around it.

Now that it’s working, perform the following tests:

Set the A4 A3 A2 A1 and B4 B3 B2 B1 inputs to the numbers shown below, and record the outputs for each setting:

What function do you think the chip is performing?

Example answer: 4-bit addition, with carry-in and carry-out.

What is the purpose of C4? Is it correct for the calculations above?

Example answer: C4 is the carry-out bit. It’s off in all results above, as it should be.

Next, set A to 1010 and B to 1111 leaving C0 off, and record the result:

GCorrect answer:

C4 0
1

S4 0
1

S3 0
1

S2 0
1

S1 0
1

Correct answer: See above

Click to select answers for these questions, assuming a 4-bit two’s-complement (i.e., signed) representation:

GCorrect answer:

Is this result correct? no
yes

Is there carry-out? no
yes

Is there overflow? no
yes

Correct answer: See above

Extra Exercises: 4-bit Ripple-Carry Adder

It turns out that once you have a 1-bit adder, you can do $n$ -bit addition by using $n$ 1-bit adders: one for each matched pair of bits in the two $n$ -bit numbers being added. The CarryOut for each pair of bits becomes the CarryIn for the next most significant pair of bits in the numbers. This is known as a ripple-carry adder.

Exercise 11:

Use the “4-bit Ripple-Carry” tab in circuitVerse to build a 4-bit adder out of 4 1-bit adders. All the necessary components are there already; you just need to hook up the inputs and outputs.

Perform the following tests to verify the circuit:

2 + 5 = Correct answer: 7

A + 3 = Correct answer: D

A + A = Correct answer: 4 (should have carry-out; this is overflow)

6 + 5 = Correct answer: B (no carry-out, but this is overflow)

F + F (with carry-in on) = Correct answer: F (carry-out and overflow)

Extra Practice

Exercise 12:

Build a 1x4 demultiplexer and/or a 4x2 encoder in CircuitVerse (create a new tab for this purpose by clicking the ‘+’ icon in the tabs tray).

Exercise 13:

Hook up two 4-bit adders to create an 8-bit adder. Make a new tab, and use “Circuit -> Insert SubCircuit” to add two copies of your “4-bit Ripple-Carry” circuit (you can also add one and then copy/paste it).

C	B	A
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

S1	S0	D
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

C	B	A
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

S1	S0	D
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

C	B	A
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

S1	S0	D
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1