PS1: Evaluating Languages
-
Due: 5:30pm Friday 9 September
- Relevant reading:
- Syllabus
- Computability and the Halting Problem
- Racket (through the section Expressions, Values, Bindings, and Environments)
- Optional: Why Undergraduates Should Learn the Principles of Programming Languages, 2011.
- Tools:
-
Overview: The purpose of this assignment is to get you thinking about the dimensions of programming languages and about evaluating and comparing programming languages. It also has exercises on computability and Racket.
-
Collaboration: All parts of this assignment fall under the standard Gilligan’s Island Rule collaboration policy. That is, you may discuss the problems and strategies for solving them with classmates and other, but all coding and written solutions must be your own individual work.
-
Submission:
At least at the beginning of this semester, CS251 work will be submitted via a combination of submitting written work via Google Docs and submitting code files via a drop folder on cs.wellesley.edu. Here’s how to submit this pset.
-
Begin by creating a Google Drive folder named yourFullName CS251 Fall 2016 Folder that you share with me and Mary Ruth Ngo with editing privileges. During the course, you will create many Google Docs in this folder, and by default they will inherit these permissions.
-
Within the folder from Step 1, create a Google Doc named yourFullName CS251 PS1.
-
Add a link to your PS1 document from your Porfolio document.
-
Now create a file folder on your computer named
yourCSAccountName_ps1. Below you will be asked to populate this file folder with various files on the assignment that you will submit (in the final step) to a drop folder on cs.wellesley.edu. -
Submit your work as described below.
-
At the top of your PS1 Google Doc, please include a header with your name, the problem set numer (e.g. PS1), and the date of submission..
-
Beneath the above header, please give a summary (for each problem or problem part) of how much time you spent on that problem or problem part. This feedback is critical for helping me design the psets to take a reasonable amount of time.
-
For Problem 1 (Concrete Syntax):
-
Put your
updateScore.pyandupdateScore.jsfiles in youryourCSAccountName_ps1folder. -
Copy the contents of these files into a Problem 1 section of your PS1 Google Doc. Make sure that code formatting is correct and easy to read. In particular, Python code must be indented properly.
-
-
For Problem 2 (Python vs. Java):
-
For parts (a) and (c), include in the Problem 2 section of your PS1 Google Doc your written answer to these parts.
-
Put your
printNames.javafile and a copy of thenames.txtfile in youryourCSAccountName_ps1folder. -
For part (b), copy the contents of
printNames.javainto the Problem 2 section of your PS1 Google Doc. Make sure that code formatting is easy to read.
-
-
For Problem 3 (Revenge of the Nerds), include your writeup in a Problem 3 section of your PS1 Google Doc.
-
For Problem 4 (Deciding Properties of Programs), include your writeup in a Problem 4 section of your PS1 Google Doc.
-
For Problem 5 (Racket Evaluation), in a Problem 5 section of your PS1 Google Doc, write one binding (or error) per line.
-
-
Copy your final
yourCSAccountName_ps1folder to yourps01cs251 drop folder on cs.wellesley.edu. This drop folder will be in acs251/drop/ps01subfolder of your account. (These folders have now been created.)
-
1. Concrete Syntax (15 points)
This problem explores how the same program can be written with different concrete syntax in different languages.
Consider the following App Inventor program, which consists of two global variable declarations and the declaration of an updateScore procedure. (This program is incomplete, since updateScore is never called.)
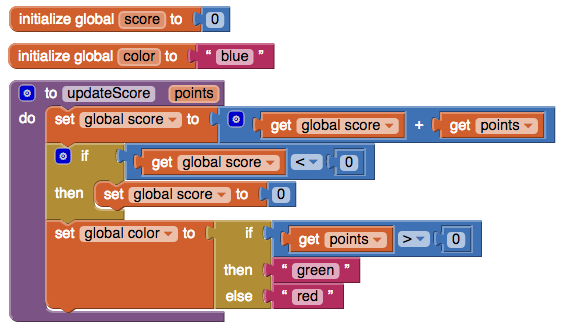
Create two files, updateScore.py and updateScore.js, that contain, respectively, (1) Python and (2) JavaScript versions of the App Inventor program.
Notes:
-
If you don’t know or can’t remember details of Python or JavaScript syntax, look it up on the Web!
-
The App Inventor example includes two global variable declarations (
scoreandcolor), a local procedure parameter declaration (points), variable references (getters) for all of these, and variable assignments (setters) for the global variables. In one of your programs, you will need an extra declaration to distinguish global from local variables. Why? (You don’t need to answer this question in your solution, but should think about it.) -
App Inventor includes both conditional statement blocks (the two left blocks below) and conditional expression blocks (the rightmost block below).

In general, a statement is a program phrase that performs an action while an expression is a program phrase that returns a value. In App Inventor, statements compose vertically to emphasize that their actions are performed sequentially from top to bottom, while expressions have plugs on their left side that denote the value returned by the expression. This value is used by the block whose socket the plug is connected to.
Both Python and JavaScript have different syntax for conditional statements vs. conditional expressions. In your programs, you should use the appropriate syntax for each one. (If you don’t know it, look it up!) In particular, do not use the conditional statement syntax to translate App Inventor’s conditional expression block!
BTW #1, App Inventor also has top-level declarations (blocks that introduce top-level named entities, like procedures and global variables). These are blocks that do not have any plugs or sockets and so cannot be connected to other blocks.
BTW #2, Racket only has declarations and expressions; it does not have statements. So Racket’s if is a condtional expression and not a conditional statement. What’s it like to program in a language without statements? You’ll find out!
-
What App Inventor calls a “procedure” is called a “function” in Python and JavaScript. The term “function” often implies that callers for the entity can return a value (i.e., function calls are expressions), whereas “procedure” often implies that callers for the entity perform an action but do not return a value (i.e., procedure calls are statements). But the usage is rather inconsistent between languages.
-
It is strongly recommended that you test your
updateScorefunctions to verify that they work correctly. E.g., you can use Canopy to testupdateScore.pyand a browser JavaScript interpreter to testupdateScore.js.
2. Python vs. Java (45 points)
All general-purpose programming languages are Turing-complete, which means that they all can be used to define the same set of computable functions. However, PLs differ in their “expressiveness”, an informal notion that attempts to capture how easy it is to write a program in one language vs. another.
This problem explores the notion of expressiveness by asking you (1) to understand a give Python program (2) to translate that program into Java and (3) to compare the resulting Java program to the original Python program.
a. Understanding a Python Program (10 points)
Below is the contents of a Python program printNames.py. The lines with comments beginning #*** were modified on Sep. 05 to make the program easier to understand and translate.
import sys
def printNames(namesFile, numEntries):
with open (namesFile, 'r') as inFile:
nameDict = {}
for line in inFile.readlines():
first, last = line.split()
if first not in nameDict:
nameDict[first] = [last]
else:
nameDict[first].append(last)
for (fst,lastList) in (sorted(nameDict.items(),
key=lambda (f,lasts): totalLength(lasts), #***MODIFIED
reverse=True))[:numEntries]:
sortedLasts = sorted(lastList, key=lambda s: (len(s), s))
print '--------\n' + fst + ' (' + str(totalLength(sortedLasts)) + '):\n' \
+ '\n'.join([str(i+1) + '. ' + s for i,s in enumerate(sortedLasts)]) #***MODIFIED (2 lines)
def totalLength(strings): #***NEW
return sum([len(s) for s in strings]) #***NEW
if __name__ == "__main__":
if len(sys.argv) != 3:
print "Usage: python findNames.py <namesFile> <numEntries>"
else:
# All kinds of errors can occur here, but don't worry about exception handling
printNames(sys.argv[1], int(sys.argv[2]))Here is a sample input file names.txt on which to run printNames.py. (This file was generated using http://homepage.net/name_generator/.)
After carefully studying the program and examining its output when run on the sample input file, describe exactly what the program does. Your description must be precise enough that someone else could implement the program from scratch based on your description without seeing the code for printNames.py. Some notes:
-
Do not give a line-by-line or step-by-step explanation of the algorithm! Instead, give a high-level specification of the input/output behavior of the program. What is expected for the inputs? What is the output of the program as a function of the inputs?
-
In this problem, you need not focus on errors/exceptions. Instead, explicitly state assumptions about the inputs for which the program will work correctly.
b. Translating the Python Program to Java (25 points):
In this part, you should write a Java program printNames.java that has the same input/output behavior as printNames.py. Your Java program need not follow exactly the same steps as the Python program; it just needs to have the same input/output behavior. Indeed, you should not copy the “Pythonic style” of the Python program, but instead use a “Java style” for your Java program, with standard data structures and methods appropriate for Java.
Here are some notes and hints for your Java program:
-
Remember that you can talk with your classmates about high-level approaches for writing this program (e.g. what classes/interfaces/methods to use) but should not share any detailed Java code with them.
-
It’s a good idea to use many classes and interfaces from the
java.utilpackage. (Useimport java.util.*;to import these.). Some particularly helpful classes/interfaces used in Lyn’s solution are the following:ArrayList,Collections,Comparator,HashMap,Iterator,List,Map.Entry,Set,Scanner. (You need not use all of these and are welcome to use others.) -
Google is your friend for finding relevant documentation/examples for the above classes. You needn’t cite “obvious” documentation sources (e.g Oracle’s Java documentation), but are encouraged to cite less obvious ones that were helpful for you.
-
The
Scannerclass is useful for reading lines from a file in Java. See slide 18-8 these Java I/O notes for how to use theScannerclass. -
Java’s built-in arrays are not a good way to translate Python’s style of extensible lists (why not?). Instead, use the
ArrayListclass for this purpose. If you’ve never usedArrayListbefore, check out an online tutorial, like this one. -
The
HashMapclass is Java’s version of Python’s dictionary. -
It’s natural to translate Python
forloops to Java’s so-calledfor eachloops, which are an abstraction for hiding details of theIteratorclass. See these notes on the Javafor eachloop. -
Do not implement your own sorting algorithm. Use
Collections.sortin conjunction with classes that implement theComparatorinterface. -
Test your Java program on the sample input file names.txt for various values of
numEntriesto verify that it has the same behavior as the Python program.
c. Reflecting on Python vs. Java (10 points)
After you have finished implementing and testing printNames.java, reflect on comparing the two languages in the context of this particular example. What aspects of Python/Java made these programs easy or hard to understand or to write? For each of the two languages, list the all the features that either (1) helped you understand/write the program or (2) got in the way of you understanding/writing the program, justifying each of your claims.
3. Revenge of the Nerds (15 points)
Read Paul Graham’s essay Revenge of the Nerds and the follow-up article Re: Revenge of the Nerds. Write a few paragraphs in which you summarize Graham’s arguments. Then explain, based on your programming experience, what you think of his arguments. What do you think is insightful? What is baloney?
4. Deciding Properties of Programs1 (15 points)
Travel for a moment to a magical land. Assume you are given the code for a function haltsNoInput. haltsNoInput decides whether a given program halts, but it works only on programs that do not take any arguments. Can you implement a solution for the general halting problem using haltsNoInput?
To be more precise, assume that:
-
You are given an implementation of a Python function
takesArguments(q, n)that takes a stringqand a nonnegative integern, and returnsTrueifqis the string representation of a legal declaration of a Python functionpthat takesnarguments and does not invoke any code that might read input from the user through the console. Ifqdoes not satisfy all these conditions,takesArguments(q, n)returnsFalse. ThetakesArgumentsfunction is definitely decidable, since such a function is indeed writable in Python. (But you are not expected to write it in this problem; you may simply assume it is given to you!) -
You are given an implementation of a Python function
haltsNoInput(r)that takes, as a string, a declaration for a Python functionrthat takes no inputs, and returns a boolean.haltsNoInput(r)has the following behavior:haltsNoInput(r)returnsTrueiftakesArguments(r,0)isTrueand the Python function described byrterminates when called on zero inputs. (Note that a function may terminate by returning a value or by throwing an exception.)haltsNoInput(r)returnsFalseif either (1)takesArguments(r,0)isFalseor (2)takesArguments(r,0)isTrue, but the Python function described byrdoes not terminate when called on zero inputs.
The question you are investigating is whether haltsNoInput can actually be written. I.e., does it describe a decidable mathematical function?
Given the above two Python functions, is it possible to write a Python function halts(p, s) that decides whether a legal one-argument Python function described by a string p would terminate when called on a string argument s? That is:
halts(p,s)returnsTrueiftakesArguments(p,1)returnsTrue,sis a string, and the Python function described bypterminates when called ons.halts(p,s)returnsFalseif either (1)takesArguments(p,1)returnsFalse, (2)sis not a string, or (3)takesArguments(p,1)returnsTrue,sis a string, and the Python function described bypdoes not terminate when called ons.
Some examples:
Many of the above descriptions are rather abstract and can be hard to understand. Here are some concrete examples that are intended to clarify things.
Consider the following Python strings definitions:
PString1 = \
'''def P(x):
return len(x)'''
PString2 = \
'''def P(x):
while True:
pass'''
PString3 = \
'''def P(x):
inputFromUser = raw_input()
return len(x + inputFromUser)'''
PString4 = \
'''def P():
return 17'''
PString5 = \
'''def P():
while True:
pass'''
SString = 'bunny'The first five definitions are string representations of Python functions named P. Here are some notes on these functions:
-
Calling the function represented by
PString1on the contents ofSStringwould return 5 (sincebunnyhas 5 characters). -
Calling the function represented by
PString2on any argument would loop infinitely. -
Calling the function represented by
PString3on the contents ofSStringwould wait for the user to enter an input string at the console, and would return the length of that string plus 5. -
Calling the function represented by
PString4on zero arguments would return 17. -
Calling the function represented by
PString5on zero arguments would loop infinitely. -
takesArguments(PString1, 1)will returnTruesincePString1is the string representation of a legal one-argument Python function. ButtakesArguments(PString1, n)for any nonnegative integernthat is not 1 will returnFalsesincePString1is the string representation of a legal one-argument Python function, and it does not takenarguments for anynother than 1. -
takesArguments(PString2, 1)will returnTruesincePString2is the string representation of a legal one-argument Python function;takesArguments(PString2, n)for any nonnegative integernthat is not 1 will returnFalsesincePString2is the string representation of a legal one-argument Python function, and it does not takenarguments for anynother than 1. -
takesArguments(PString3, n)will returnFalsefor any nonnegative integern. AlthoughPString3is the string representation of a legal one-argument Python function, that function reads user input from the console, so it will still returnFalsewhennis 1. -
takesArguments(PString4, 0)will returnTruesincePString4is the string representation of a legal zero-argument Python function.takesArguments(PString4, n)for any nonnegative integernthat is not 0 will returnFalsesincePString2is the string representation of a legal zero-argument Python function, and it does not takenarguments for anynother than 0. -
takesArguments(PString5, 0)will returnTruesincePString5is the string representation of a legal zero-argument Python function.takesArguments(PString5, n)for any nonnegative integernthat is not 0 will returnFalsesincePString2is the string representation of a legal zero-argument Python function, and it does not takenarguments for anynother than 0. -
takesArguments(SString, n)will returnFalsefor any nonnegative integernsinceSStringis not the string representation of a Python function. -
If
haltscould be written, the following would all returnTrue:halts(PString1, SString)halts(PString1, PString1)(and similarly for second argumentPString2throughPString5)
- If
haltscould be written, the following would all returnFalse:halts(PString2, s)for any string inputs, because the function denoted byPString2loops on all arguments.halts(PString3, s)for any string inputs, because thetakesArguments(PString3, 1)returnsFalsehalts(PString4, s)for any string inputs, because thetakesArguments(PString4, 1)returnsFalsehalts(PString5, s)for any string inputs, because thetakesArguments(PString5, 1)returnsFalsehalts(SString, v)for any valuev, becausetakesArguments(SString, 1)returnsFalse(it does not represent a Python function)halts(PString1, n)for any number inputn, because a numbernis not a string
-
If
haltsNoInputcould be written, thenhaltsNoInput(PString4)would returnTrue: - If
haltsNoInputcould be written, then all the following would returnFalse:haltsNoInput(PString5), because the function denoted byPString5loops infinitely when called on zero arguments.haltsNoInput(PString1), becausetakesArguments(PString1, 0)returnsFalsehaltsNoInput(PString2), becausetakesArguments(PString2, 0)returnsFalsehaltsNoInput(PString3), becausetakesArguments(PString3, 0)returnsFalsehaltsNoInput(SString), becausetakesArguments(SString, 0)returnsFalse(it does not represent a Python function)
How to answer:
A formal proof is not required.
- If the halting problem can be solved assuming you are given
haltsNoInputas described, give a pseudocode implementation ofhalts(p, s)and describe in prose how it works. - If the halting problem cannot be solved using
haltsNoInput, explain in prose why not. - Finally, does your answer imply anything about the possibility of implementing
haltsNoInput? Answer in prose.
5. Racket Evaluation (10 points)
For each of the following Racket definitions, write the value to which the variable will be bound, or “error” if evaluating this binding would result in an error.
Write your answers, with one line per definition, in order, in the form:
x --> 7
y --> 3
z: divide-by-zero errormeaning that variable x is bound to value 7, variable y is bound to value 3, and evaluating the binding for z results in a divide-by-zero error.
Predict the answers without running the code. You may find it useful to write evaluation derivations, leaving blanks for the result values as you build the derivation, and then filling in the results once you begin to reach values, but you do not need to submit derivations. You may also check your manually evaluated answers by running each binding in order in the DrRacket REPL. (Instructions on using DrRacket are here.)
#lang racket
(define a 5)
(define b (* a a))
(define c (+ (* 2 a) (- b a)))
(define d (+ a b c))
(define e (+ a))
(define f (+))
(define g (*))
(define h b)
(define i (if (< a 0) 7 (quotient 43 a)))
(define j (if (= a 0) 11 (remainder 43 a)))
(define k (/ i j))
(define l (< a b))
(define m (= b c))
(define n (< b c d))
(define o (+ a m))
(define p (< a m) )
(define q (if a b c))
(define r (if l m n))
(define s (if (if (< i j) m l)
(if (> a c) (+ a c) (* a c))
(if (< a b) (+ a b) (* a b))))
(define t (= (if (< b c)
(* (remainder (- (* a b) (* 2 a)) c) (- (quotient d b)))
(* (- (+ d (* (* a b) (quotient d a))))))
(- (* (/ (- c a) (- a 1)) (quotient b (if (> a c) i j))))))
(define u (if (> i j) (< a 0) (< (< b c) a)))
(define v (if (<= i j) (< a 0) (< (< b c) a)))-
This problem is adapted from a problem by Stephen Freund at Williams College, by permission. ↩