PS7: Set Yourself Free
- Due: Friday, Dec 02.
- Notes:
- This pset contains two solo problems worth 25 points.
- This pset has 100 total points.
- The problems needn’t be done in order. Feel free to jump around.
- Submission:
- In your yourFullName CS251 Fall 2016 Folder, create a Google Doc named yourFullName CS251 PS7.
- At the top of your yourFullName CS251 PS7 doc, include your name, problem set number, date of submission, and an approximation of how long each problem part took.
- For all parts of all problems, include all answers (including SML code) in your PS7 google doc. Format code using a fixed-width font, like Consolas or Courier New. You can use a small font size if that helps.
- For Problem 1 (first solo problem), include the English answers to parts 1a and 1b (including any Racket code examples) in your PS7 google doc.
- In Problems 2 through 5, you will create the following code files from starter files populating your
~wx/cs251/sml/ps7directory on your wx Virtual Machine:- Problem 2:
yourAccountName-marbles.sml - Problem 3:
yourAccountName-TTTreeFuns.sml - Problem 4:
yourAccountName-FunSet.sml - Problem 5:
yourAccountName-OperationTreeSet.sml
Drop copies of the above four files as well asTTTree.smlinto in your~/cs251/drop/ps07drop folder oncs.wellesley.edu.
- Problem 2:
- For Problems 2 through 5 you should include all functions from the four files named
yourAccountName...in your Google Doc (so that I can comment on them). - For Problem 4b, don’t forget to include your English answers in your Google Doc.
Starting this Problem Set
Problems 2 through 5 involve starter files in the ~wx/cs251/sml/ps7 directory in your wx Virtual Machine.
To create this directory, execute the following two commands in a wx VM shell:
cd ~/cs251/sml
git pull origin master1. Solo Problem: Conjunction Junction (10 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
We have seen that Racket’s and is not a function, but syntactic sugar. For example, if exp1 and exp2 are expressions, (and exp1 exp2 ) desugars to (if exp1 exp2 #f).
Suppose we define a function and-fun as follows:
(define (and-fun a b) (if a b #f))Although and and and-fun seem similar, there are some subtle but important differences between them.
-
(8 points) For each of the following three function definitions using
and, explain whether the defined functions would or would not have exactly the same behavior ifandwere replaced byand-fun. In this problem ``behavior’’ not only means the input/output behavior of the function, but also how much work it does (i.e., how many operations does it perform?) Behavior also includes errors; are there situations in which one ofandorand-fungives an error, but the other does not?Explain each answer. In cases where behaviors are different, give one or more concrete examples in which the two versions behave differently, and explain why they behave differently.
(define (between x lo hi) (and (<= lo x) (<= x hi))) (define (first-positive? nums) (and (not (null? nums)) (> (first nums) 0))) (define (all-negative? nums) (foldr and #t (map (λ (n) (< n 0)) nums)))Note: The
all-negative?function above has a syntax error, but that is intentional. Understanding this error is part of the problem. Hint: is there still an error ifandis replaced byand-funinall-negative?. -
(2 points) Is Java’s
&&construct more like (1) Racket’sandor (2) theand-funfunction defined above? Briefly explain your answer, using examples as appropriate.
2. Solo Problem: Losing Your Marbles (15 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
Put all your definitions for this problem in the starter file ~/cs251/sml/ps7/marbles.sml. When you finish this problem, rename the file to yourAccountName-ps7-marbles.sml before you submit it.
In this problem, you will define an SML function satisfying the following specification:
val marbles: int -> int -> int list list
Assume that
mis a non-negative integer and thatcis a positive integer. Givenmmarbles and a row ofccups,marbles m creturns a sorted list of all configurations whereby allmmarbles are distributed among theccups. Each configuration should be a list of lengthcwhose elements are integers between 0 andmand the sum of whose elements ism. The returned list should be ordered lexicographically (i.e., in dictionary order).
At the end of this problem description are numerous sample invocations of the marbles function.
Your task is to define the marbles function in SML so that it satisfies the above specification and has the same behavior as the sample invocations below.
Notes:
-
As usual, you should use divide/conquer/glue as your problem-solving strategy. Strive to make your solution as simple as possible. For example, do not use more base cases than are strictly necessary.
-
Don’t forget the very powerful notion of “wishful” thinking, in which you blindly apply a recursive function to smaller versions of the same problem and combine their results. Study the examples carefully to see how the result of a call to
marblesis stitched together from the results of calls to “smaller” versions ofmarbles. -
Your
marblesfunction should generate the elements in sorted order without calling any kind of sorting function. -
You are expected to use higher-order list functions where they can simplify your definition.
-
The stater file begins with the following helper functions, which you might find useful:
fun cons x ys = x :: ys (* curried list consing operator *) fun range lo hi = (* list all ints from lo up to (but not including) hi *) List.tabulate(hi - lo, fn i => i + lo)Reminder: these and other helper functions must be defined above your definition of
marbles, because definition order matters in SML. -
Feel free to define any additional auxiliary functions you find helpful.
-
To display elements beyond the default cutoff length for lists, use
Control.Print.printLength := 100;
- Control.Print.printLength := 100;
val it = () : unit
- marbles 0 1;
val it = [[0]] : int list list
- marbles 0 2;
val it = [[0,0]] : int list list
- marbles 0 3;
val it = [[0,0,0]] : int list list
- marbles 0 4;
val it = [[0,0,0,0]] : int list list
- marbles 1 1;
val it = [[1]] : int list list
- marbles 1 2;
val it = [[0,1],[1,0]] : int list list
- marbles 1 3;
val it = [[0,0,1],[0,1,0],[1,0,0]] : int list list
- marbles 1 4;
val it = [[0,0,0,1],[0,0,1,0],[0,1,0,0],[1,0,0,0]] : int list list
- marbles 2 1;
val it = [[2]] : int list list
- marbles 2 2;
val it = [[0,2],[1,1],[2,0]] : int list list
- marbles 2 3;
val it = [[0,0,2],[0,1,1],[0,2,0],[1,0,1],[1,1,0],[2,0,0]] : int list list
- marbles 2 4;
val it =
[[0,0,0,2],[0,0,1,1],[0,0,2,0],[0,1,0,1],[0,1,1,0],[0,2,0,0],[1,0,0,1],
[1,0,1,0],[1,1,0,0],[2,0,0,0]] : int list list
- marbles 3 1;
val it = [[3]] : int list list
- marbles 3 2;
val it = [[0,3],[1,2],[2,1],[3,0]] : int list list
- marbles 3 3;
val it =
[[0,0,3],[0,1,2],[0,2,1],[0,3,0],[1,0,2],[1,1,1],[1,2,0],[2,0,1],[2,1,0],
[3,0,0]] : int list list
- marbles 3 4;
val it =
[[0,0,0,3],[0,0,1,2],[0,0,2,1],[0,0,3,0],[0,1,0,2],[0,1,1,1],[0,1,2,0],
[0,2,0,1],[0,2,1,0],[0,3,0,0],[1,0,0,2],[1,0,1,1],[1,0,2,0],[1,1,0,1],
[1,1,1,0],[1,2,0,0],[2,0,0,1],[2,0,1,0],[2,1,0,0],[3,0,0,0]]
: int list list
- marbles 4 1;
val it = [[4]] : int list list
- marbles 4 2;
val it = [[0,4],[1,3],[2,2],[3,1],[4,0]] : int list list
- marbles 4 3;
val it =
[[0,0,4],[0,1,3],[0,2,2],[0,3,1],[0,4,0],[1,0,3],[1,1,2],[1,2,1],[1,3,0],
[2,0,2],[2,1,1],[2,2,0],[3,0,1],[3,1,0],[4,0,0]] : int list list
- marbles 4 4;
val it =
[[0,0,0,4],[0,0,1,3],[0,0,2,2],[0,0,3,1],[0,0,4,0],[0,1,0,3],[0,1,1,2],
[0,1,2,1],[0,1,3,0],[0,2,0,2],[0,2,1,1],[0,2,2,0],[0,3,0,1],[0,3,1,0],
[0,4,0,0],[1,0,0,3],[1,0,1,2],[1,0,2,1],[1,0,3,0],[1,1,0,2],[1,1,1,1],
[1,1,2,0],[1,2,0,1],[1,2,1,0],[1,3,0,0],[2,0,0,2],[2,0,1,1],[2,0,2,0],
[2,1,0,1],[2,1,1,0],[2,2,0,0],[3,0,0,1],[3,0,1,0],[3,1,0,0],[4,0,0,0]]
: int list list
- marbles 5 1;
val it = [[5]] : int list list
- marbles 5 2;
val it = [[0,5],[1,4],[2,3],[3,2],[4,1],[5,0]] : int list list
- marbles 5 3;
val it =
[[0,0,5],[0,1,4],[0,2,3],[0,3,2],[0,4,1],[0,5,0],[1,0,4],[1,1,3],[1,2,2],
[1,3,1],[1,4,0],[2,0,3],[2,1,2],[2,2,1],[2,3,0],[3,0,2],[3,1,1],[3,2,0],
[4,0,1],[4,1,0],[5,0,0]] : int list list
- marbles 5 4;
val it =
[[0,0,0,5],[0,0,1,4],[0,0,2,3],[0,0,3,2],[0,0,4,1],[0,0,5,0],[0,1,0,4],
[0,1,1,3],[0,1,2,2],[0,1,3,1],[0,1,4,0],[0,2,0,3],[0,2,1,2],[0,2,2,1],
[0,2,3,0],[0,3,0,2],[0,3,1,1],[0,3,2,0],[0,4,0,1],[0,4,1,0],[0,5,0,0],
[1,0,0,4],[1,0,1,3],[1,0,2,2],[1,0,3,1],[1,0,4,0],[1,1,0,3],[1,1,1,2],
[1,1,2,1],[1,1,3,0],[1,2,0,2],[1,2,1,1],[1,2,2,0],[1,3,0,1],[1,3,1,0],
[1,4,0,0],[2,0,0,3],[2,0,1,2],[2,0,2,1],[2,0,3,0],[2,1,0,2],[2,1,1,1],
[2,1,2,0],[2,2,0,1],[2,2,1,0],[2,3,0,0],[3,0,0,2],[3,0,1,1],[3,0,2,0],
[3,1,0,1],[3,1,1,0],[3,2,0,0],[4,0,0,1],[4,0,1,0],[4,1,0,0],[5,0,0,0]]
: int list list3. 2-3 Trees (25 points)
In this problem you will use SML to implement aspects of 2-3 trees, a particular search tree data structure that is guaranteed to be balanced.
Begin by skimming pages 1 through 7 of this handout on 2-3 trees. (I create this handout for CS230 in Fall, 2004, but we no longer teach 2-3 trees in that course).
In a 2-3 tree, there are three kinds of nodes: leaves, 2-nodes, and 3-nodes. Together, these can be expressed in SML as follows:
datatype TTTree = (* 2-3 tree of ints *)
L (* Leaf *)
| W of TTTree * int * TTTree (* tWo node *)
| H of TTTree * int * TTTree * int * TTTree (* tHree node *)For simplicity, we will only consider 2-3 trees of integers, though they can be generalized to handle any type of value.
For conciseness in constructing and displaying large trees, the three constructors have single-letter names. For example, below are the pictures of four sample 2-3 trees from the handout and how they would be expressed with these constructors:

val t1 = W( W(W(L,1,L), 2, W(L,3,L)), 4, W(W(L,5,L), 6, W(L,7,L)))
val t2 = H( W(L,1,L), 2, H(L,3,L,4,L), 5, H(L,6,L,7,L))
val t3 = H( H(L,1,L,2,L), 3, W(L,4,L), 5, H(L,6,L,7,L))
val t4 = H( H(L,1,L,2,L), 3, H(L,4,L,5,L), 6, W(L,7,L))As explained in the handout on 2-3 trees, a 2-3 tree is only valid it it satisfies two additional properties:
- The ordering property:
- In a 2-node with left subtree l, value X, and right subtree r, (all values in l) ≤ X ≤ (all values in r).
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, (all values in l) ≤ X ≤ (all values in m) ≤ Y ≤ (all values in r).
- The height property (called path length invariant in the handout): in a 2-node or 3-node, the height of all subtrees must be exactly the same.
The height property guarantees that a valid 2-3 tree is balanced. Together, these two properties guarantee that a 2-3 tree is efficiently searchable.
Your ~wx/cs251/sml/ps7 folder includes the file TTTree.sml, which contains the TTTree dataytype defined above as well as numerous examples of valid and invalid 2-3 trees that are instances of this datatype. Note that t and vt are used for valid trees, io is used for invalidly ordered trees, and ih is used for invalid height trees.
| tree name | elements | ordered? | satisfies the height property? |
|---|---|---|---|
| t1 | [1,…,7] | Yes | Yes, with height 3 |
| t2 | [1,…,7] | Yes | Yes, with height 2 |
| t3 | [1,…,7] | Yes | Yes, with height 2 |
| t4 | [1,…,7] | Yes | Yes, with height 2 |
| vt0 | [] | Yes | Yes, with height 0 |
| vt2 | [1,2] | Yes | Yes, with height 1 |
| vt17 | [1,…,17] | Yes | Yes, with height 3 |
| vt20 | [1,…,20] | Yes | Yes, with height 4 |
| vt44 | [1,…,44] | Yes | Yes, with height 5 |
| vt92 | [1,…,92] | Yes | Yes, with height 6 |
| io2 | [1,2] | No | Yes, with height 1 |
| io7 | [1,…,7] | No | Yes, with height 2 |
| io17 | [1,…,17] | No | Yes, with height 3 |
| io20 | [1,…,20] | No | Yes, with height 4 |
| io44 | [1,…,44] | No | Yes, with height 5 |
| io92 | [1,…,92] | No | Yes, with height 6 |
| ih2 | [1,2] | Yes | No |
| ih7 | [1,…,7] | Yes | No |
| ih17 | [1,…,17] | Yes | No |
| ih20 | [1,…,20] | Yes | No |
| ih44 | [1,…,44] | Yes | No |
| ih92 | [1,…,92] | Yes | No |
These trees are used to define two lists:
val validTrees = [vt0, vt2, t2, t3, t4, t1, vt17, vt20, vt44, vt92]
val invalidTrees = [io2, io7, io17, io20, io44, io92,
ih2, ih9, ih17, ih20, ih44, ih92]In this problem you will (1) implement a validity test for 2-3 trees and (2) implement the effcient 2-3 insertion algorithm from the handout on 2-3 trees.
Your ~wx/cs251/sml/ps7 folder also includes the starter file TTTreeFuns.sml. In this file, flesh out the missing definitions as specified below. When you finish this problem, rename the file to yourAccountName-TTTreeFuns.sml before you submit it.
-
satisfiesOrderingProperty(7 points)In this part, you will implement a function
satisfiesOrderingProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree ordering property andfalseif it does not. An easy way to do this is to define two helper functions:elts: TTTree -> int listreturns a list of all the elements of the tree in in-order — i.e.,- In a 2-node with left subtree l, value X, and right subtree r, all values in l are listed before X, which is listed before all elements in r.
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, all values in l are listed before X, which is listed before all values in m, which are listed before Y , which is listed before all values in r.
isSorted: int list -> boolreturnstrueif the list of integers is in sorted order andfalseotherwise.
For example:
- elts vt17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] : int list - elts io17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,17,16] : int list - isSorted(elts vt17); val it = true : bool - isSorted(elts io17); val it = false : boolUsing these two helper functions,
satisfiesOrderingPropertycan be implemented as:fun satisfiesOrderingProperty t = isSorted(elts t)For example:
- map satisfiesOrderingProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesOrderingProperty invalidTrees; val it = [false,false,false,false,false,false,true,true,true,true,true,true] : bool listNotes:
-
Once (and only once) execute
use "TTTree.sml";to load the
TTTreedatatype and example trees. Then every time you change the fileTTTreeFuns.sml, executeuse "TTTreeFuns.sml" -
If you haven’t done so already, read these notes on SML/NJ and Emacs SML Mode and follow the advice there. In particular, it is strongly recommended that you create an SML interpreter within a
*sml*buffer in Emacs. Then you can useM-pandM-nto avoid retyping your test expressions. -
You may need to execute
Control.Print.printLength := 100;in order to see all the list elements. -
Implement
isSortedusing the same zipping approach you used in PS3. You do zipping in SML viaListPair.zipfrom the ListPair module.List.allfrom the List module is also helpful.
-
satisfiesHeightProperty(6 points)In this part, you will implement a function
satisfiesHeightProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree height property andfalseif it does not. An easy way to do this is to definesatisfiesHeightPropertyasfun satisfiesHeightProperty t = Option.isSome (height t)where
Option.isSomeis a function from the Option module that determines if anoptionvalue is aSOME(vs. aNONE) andheightis a function with typeTTTree -> option intsuch thatheight treturnsSOME hiftsatisfies the height property with heighthand otherwise returnsNONE.Implement the
heightfunction by fleshing out this skeleton:(* height: TTTree -> int option *) fun height L = (* return an appropriate option value here *) | height (W(l, _, r)) = (case (height(l), height(r)) of (* put appropriate pattern clauses here *)) | (* handle the H case here, similarly to the W case *)For example:
- map height validTrees; val it = [SOME 0,SOME 1,SOME 2,SOME 2,SOME 2,SOME 3,SOME 3,SOME 4,SOME 5,SOME 6] : int option list - map height invalidTrees; val it = [SOME 1,SOME 2,SOME 3,SOME 4,SOME 5,SOME 6,NONE,NONE,NONE,NONE,NONE,NONE] : int option listNotes:
-
It’s important to enclose the
caseexpressions withinheightin parens to distinguish the pattern clauses of thecaseexpression from those of theheightfunction definition. -
Once
heightis defined,satisfiesHeightPropertyis defined:- map satisfiesHeightProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesHeightProperty invalidTrees; val it = [true,true,true,true,true,true, false,false,false,false,false,false] : bool list -
Once both
satisfiesOrderingPropertyandsatisfiesHeightPropertyare defined, it is trivial to define a functionisValid: TTTree -> boolthat returnstrueif a given 2-3 tree is valid andfalseotherwise.fun isValid t = satisfiesOrderingProperty t andalso satisfiesHeightProperty t - map isValid validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map isValid invalidTrees; val it = [false,false,false,false,false,false, false,false,false,false,false,false] : bool list
-
-
insert(12 points) In this part, you will implement the insertion algorithm for 2-3 trees as described on pages 3 to 5 of the handout on 2-3 trees. You will not implement the special cases described on page 6 .The insertion algorithm is a recursive algorithm that uses the notion of a pseudo 2-node that is “kicked up” in certain cases and handled specially in the upward phase of the recursion. To distinguish an insertion result that is a regular 2-3 tree from a pseudo 2-node that is “kicked up”, we use the following datatype:
datatype InsResult = Tree of TTTree | KickedUp of TTTree * int * TTTree (* pseudo 2-node "kicked up" from below *)You will implement 2-3 tree insertion via a pair of functions:
-
(insert v t)returns the newTTTreethat results from inserting a given intvinto a given treet.inserthas typeint -> TTTree -> TTTree. -
(ins v t)is a helper function that returns the instance ofInsResultthat results from inserting a given intvinto a given treet.inshas typeint -> TTTree -> InsResult.
Your implementation should flesh out the following code skeleton by turning the pictures on pages 3 to 5 from the handout on 2-3 trees into SML code.
(* insert: int -> TTTree -> TTTree *) fun insert v t = case ins v t of Tree t => t | KickedUp(l, w, r) => W(l, w, r) and (* "and" glues together mutually recursive functions *) (* ins: int -> TTTree -> InsResult *) ins v L = KickedUp (L, v, L) | ins v (W(l, X, r)) = if v <= X then (case ins v l of Tree l' => Tree(W(l', X, r)) | KickedUp (l', w, m) => Tree(H(l', w, m, X, r))) else (* flesh this out *) | (* handle an H node similarly to the W node based on rules from the handout *)Notes:
-
The
insfunction should only callinsrecursively and should not callinsert. -
An easy way to test
insertis to call the followinglistToTTTreefunction on a list of numbers generated byrange. (These are already defined in your starter file.) Note that you may need to increase the print depth (viaControl.Print.printDepth := 100) in order to see all the details of the printed trees:fun listToTTTree xs = foldl (fn (x,t) => insert x t) L xs fun range lo hi = if lo >= hi then [] else lo :: (range (lo + 1) hi) - listToTTTree (range 1 8); val it = W (W (W #,2,W #),4,W (W #,6,W #)) : TTTree - listToTTTree (range 1 17); val it = W (W (W #,4,W #),8,W (W #,12,W #)) : TTTree - Control.Print.printDepth := 100; val it = () : unit - listToTTTree (range 1 7); val it = H (W (L,1,L),2,W (L,3,L),4,H (L,5,L,6,L)) : TTTree - listToTTTree (range 1 18); val it = W (W (W (W (L,1,L),2,W (L,3,L)),4,W (W (L,5,L),6,W (L,7,L))),8, W (W (W (L,9,L),10,W (L,11,L)),12, H (W (L,13,L),14,W (L,15,L),16,W (L,17,L)))) : TTTree - listToTTTree (range 1 45); val it = W (W (W (W (W (L,1,L),2,W (L,3,L)),4,W (W (L,5,L),6,W (L,7,L))),8, W (W (W (L,9,L),10,W (L,11,L)),12,W (W (L,13,L),14,W (L,15,L)))),16, H (W (W (W (L,17,L),18,W (L,19,L)),20,W (W (L,21,L),22,W (L,23,L))),24, W (W (W (L,25,L),26,W (L,27,L)),28,W (W (L,29,L),30,W (L,31,L))),32, H (W (W (L,33,L),34,W (L,35,L)),36,W (W (L,37,L),38,W (L,39,L)),40, W (W (L,41,L),42,H (L,43,L,44,L))))) : TTTree -
Unfortunately, inserting elements in sequential order as above tends to create 2-3 trees with almost all 2-nodes and very few 3-nodes. It turns out a better way is to mix up the order of insertion as is done in the following code for
makeTTTree. This results in trees that have a good mix of 2-nodes and 3-nodes:(* Return list that has all ints in nums, but those not divisible by 3 come before those divisible by three *) fun arrangeMod3 nums = let val (zeroMod3, notZeroMod3) = List.partition (fn n => (n mod 3) = 0) nums in notZeroMod3 @ zeroMod3 end (* Make a 2-3 tree with elements from 1 up to and including size. Use arrangeMod3 to mix up numbers and lead to more 3-nodes than we'd get with sorted integers lists *) fun makeTTTree size = listToTTTree (arrangeMod3 (range 1 (size + 1))) - makeTTTree 17; val it = H (W (W (L,1,L),2,H (L,3,L,4,L)),5,W (H (L,6,L,7,L),8,H (L,9,L,10,L)),11, H (H (L,12,L,13,L),14,W (L,15,L),16,W (L,17,L))) : TTTree - makeTTTree 44; val it = W (W (W (W (W (L,1,L),2,H (L,3,L,4,L)),5,W (H (L,6,L,7,L),8,H (L,9,L,10,L))), 11, W (W (H (L,12,L,13,L),14,H (L,15,L,16,L)),17, W (H (L,18,L,19,L),20,H (L,21,L,22,L)))),23, W (W (W (H (L,24,L,25,L),26,H (L,27,L,28,L)),29, W (H (L,30,L,31,L),32,H (L,33,L,34,L))),35, W (W (H (L,36,L,37,L),38,H (L,39,L,40,L)),41, W (W (L,42,L),43,W (L,44,L))))) : TTTree -
Finally, to test your insertion implementation more extensively, try
(testInsert 1000)with the following function, which will usemakeTTTreeto create 2-3 trees containing 0 elements to 1000 elements and warn you of any invalid trees.fun testInsert upToSize = let val pairs = map (fn n => (n, makeTTTree n)) (range 0 (upToSize + 1)) val (validPairs, invalidPairs) = List.partition (fn (_,t) => isValid t) pairs val wrongElts = List.filter (fn (n,t) => (elts t) <> (range 1 (n + 1))) validPairs in if (null invalidPairs) andalso (null wrongElts) then (print "Passed all test cases\n"; []) else if (not (null invalidPairs)) then (print "There are invalid trees in the following cases\n"; invalidPairs) else (print "The elements or element order is wrong in the following cases\n"; wrongElts) end - testInsert 1000; Passed all test cases val it = [] : (int * TTTree) list
-
4. Fun Sets (25 points)
In SML, we can implement abstract data types in terms of familiar structures like lists and trees. But we can also use functions to implement data types. In this problem, you will investigate a compelling example of using functions to implement sets.
Your ~wx/cs251/sml/ps7 folder contains the starter file FunSet.sml. This includes the same SET signature we studied in class:
signature SET =
sig
(* The type of sets *)
type ''a t
(* An empty set *)
val empty : ''a t
(* Construct a single-element set from that element. *)
val singleton : ''a -> ''a t
(* Check if a set is empty. *)
val isEmpty : ''a t -> bool
(* Return the number of elements in the set. *)
val size : ''a t -> int
(* Check if a given element is a member of the given set. *)
val member : ''a -> ''a t -> bool
(* Construct a set containing the given element and all elements
of the given set. *)
val insert : ''a -> ''a t -> ''a t
(* Construct a set containing all elements of the given set
except for the given element. *)
val delete : ''a -> ''a t -> ''a t
(* Construct the union of two sets. *)
val union : ''a t -> ''a t -> ''a t
(* Construct the intersection of two sets. *)
val intersection : ''a t -> ''a t -> ''a t
(* Construct the difference of two sets
(all elements in the first set but not in the second.) *)
val difference : ''a t -> ''a t -> ''a t
(* Construct a set from a list of elements.
Do not assume the list elements are unique. *)
val fromList : ''a list -> ''a t
(* Convert a set to a list without duplicates.
The elements in the resulting list may be in any order. *)
val toList : ''a t -> ''a list
(* Construct a set from a predicate function:
the resulting set should contain all elements for which
this predicate function returns true.
This acts like math notation for sets. For example:
{ x | x mod 3 = 0 }
would be written:
fromPred (fn x => x mod 3 = 0)
*)
val fromPred : (''a -> bool) -> ''a t
(* Convert a set to a predicate function. *)
val toPred : ''a t -> ''a -> bool
(* Convert a set to a string representation, given a function
that converts a set element into a string representation. *)
val toString : (''a -> string) -> ''a t -> string
(* Convert a set to a list without duplicates.
The elements in the resulting list may be in any order. *)
val toList : ''a t -> ''a list
(* Construct a set from a predicate function:
the resulting set should contain all elements for which
this predicate function returns true.
This acts like math notation for sets. For example:
{ x | x mod 3 = 0 }
would be written:
fromPred (fn x => x mod 3 = 0)
*)
val fromPred : (''a -> bool) -> ''a t
(* Convert a set to a predicate function. *)
val toPred : ''a t -> ''a -> bool
(* Convert a set to a string representation, given a function
that converts a set element into a string representation. *)
val toString : (''a -> string) -> ''a t -> string
endIn this problem, you will flesh out the skeleton of the FunSet structure below. When you finish this probelm, you should rename this file to yourAccountName-FunSet.sml before you submit it.
exception Unimplemented (* Placeholder during development. *)
exception Unimplementable (* Impossible to implement *)
(* Implement a SET ADT using predicates to represent sets. *)
structure FunSet :> SET = struct
(* Sets are represented by predicates. *)
type ''a t = ''a -> bool
(* The empty set is a predicate that always returns false. *)
val empty = fn _ => false
(* The singleton set is a predicate that returns true for exactly one element *)
val singleton x = fn y => x=y
(* Determining membership is trivial with a predicate *)
val member x pred = pred x
(* complete this structure by replacing "raise Unimplemented"
with implementations of each function. Many of the functions
*cannot* be implemented; for those, use raise Unimplementable
as there implementation *)
fun isEmpty _ = raise Unimplemented
fun size _ = raise Unimplemented
fun member _ = raise Unimplemented
fun insert _ = raise Unimplemented
fun delete _ = raise Unimplemented
fun union _ = raise Unimplemented
fun intersection _ = raise Unimplemented
fun difference _ = raise Unimplemented
fun fromList _ = raise Unimplemented
fun toList _ = raise Unimplemented
fun fromPred _ = raise Unimplemented
fun toPred _ = raise Unimplemented
fun toString _ = raise Unimplemented
endThe fromPred and toPred operations are based on the observation that a membership predicate describes exactly which elements are in the set and which are not. Consider the following example:
- val s235 = fromPred (fn x => (x = 2) orelse (x = 3) orelse (x = 5));
val s235 = - : int t
- member 2 s235;
val it = true : bool
- member 3 s235;
val it = true : bool
- member 5 s235;
val it = true : bool
- member 4 s235;
val it = false : bool
- member 100 s235;
val it = false : boolThe set s235 consists of exactly those elements satisfying the predicate passed to fromPred – in this case, the integers 2, 3, and 5.
Defining sets in terms of predicates has many benefits. Most important, it is easy to specify sets that have infinite numbers of elements! For example, the set of all even integers can be expressed as:
fromPred (fn x => (x mod 2) = 0)This predicate is true of even integers, but is false for all other integers. The set of all values of a given type is expressed as fromPred (fn x => true). Many large finite sets are also easy to specify. For example, the set of all integers between 251 and 6821 (inclusive) can be expressed as
fromPred (fn x => (x >= 251) && (x <= 6821))Although defining sets in terms of membership predicates is elegant and has many benefits, it has some big downsides. The biggest one is that several functions in the SET signature simply cannot be implemented. You will explore this downside in this problem.
-
(17 points) Flesh out the code skeleton for the
FunSetstructure inFunSet.sml. Some value bindings cannot be implement; for these, useraise Unimplementableas the implementation.At the end of the starter file are the following commented out test cases. Uncomment these test cases to test your implementation. Feel free to add additional tests.
open FunSet (* range helper function *) fun range lo hi = if lo >= hi then [] else lo::(range (lo + 1) hi) (* Test an int pred set on numbers from 0 to 100, inclusive *) fun intPredSetToList predSet = List.filter (toPred predSet) (range 0 101) val mod2Set = fromPred (fn x => x mod 2 = 0) val mod3Set = fromPred (fn x => x mod 3 = 0) val lowSet = fromList (range 0 61) val highSet = fromList (range 40 101) val smallSet = insert 17 (insert 19 (insert 23 (singleton 42))) val smallerSet = delete 23 (delete 19 (delete 57 smallSet)) (* Be sure to print all details *) val _ = Control.Print.printLength := 101; val smallSetTest = intPredSetToList(smallSet) val smallerSetTest = intPredSetToList(smallerSet) val mod3SetTest = intPredSetToList(mod3Set) val mod2SetUnionMod3SetTest = intPredSetToList(union mod2Set mod3Set) val mod2SetIntersectionMod3SetTest = intPredSetToList(intersection mod2Set mod3Set) val mod2SetDifferenceMod3SetTest = intPredSetToList(difference mod2Set mod3Set) val mod3SetDifferenceMod2SetTest = intPredSetToList(difference mod3Set mod2Set) val bigIntersection = intPredSetToList(intersection (intersection lowSet highSet) (intersection mod2Set mod3Set)) val bigDifference = intPredSetToList(difference (difference lowSet highSet) (difference mod2Set mod3Set))For the test expressions generating lists, the results are as follows:
val smallSetTest = [17,19,23,42] : int list val smallerSetTest = [17,42] : int list val mod3SetTest = [0,3,6,9,12,15,18,21,24,27,30,33,36,39,42,45,48,51,54,57,60,63,66,69,72,75, 78,81,84,87,90,93,96,99] : int list val mod2SetUnionMod3SetTest = [0,2,3,4,6,8,9,10,12,14,15,16,18,20,21,22,24,26,27,28,30,32,33,34,36,38,39, 40,42,44,45,46,48,50,51,52,54,56,57,58,60,62,63,64,66,68,69,70,72,74,75,76, 78,80,81,82,84,86,87,88,90,92,93,94,96,98,99,100] : int list val mod2SetIntersectionMod3SetTest = [0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96] : int list val mod2SetDifferenceMod3SetTest = [2,4,8,10,14,16,20,22,26,28,32,34,38,40,44,46,50,52,56,58,62,64,68,70,74,76, 80,82,86,88,92,94,98,100] : int list val mod3SetDifferenceMod2SetTest = [3,9,15,21,27,33,39,45,51,57,63,69,75,81,87,93,99] : int list val bigIntersection = [42,48,54,60] : int list val bigDifference = [0,1,3,5,6,7,9,11,12,13,15,17,18,19,21,23,24,25,27,29,30,31,33,35,36,37,39] : int list -
(8 points) For each function that you declared being unimplementable, explain in English why it is unimplementable. Give concrete examples where appropriate.
5. Operation Tree Sets (25 points)
A very different way of representing a set as a tree is to remember the structure of the set operations empty, insert, delete, union, intersection, and difference used to create the set. For example, consider the set t created as follows:
val s = (delete 4 (difference (union (union (insert 1 empty)
(insert 4 empty))
(union (insert 7 empty)
(insert 4 empty)))
(intersection (insert 1 empty)
(union (insert 1 empty)
(insert 6 empty)))))Abstractly, s is the singleton set {7}. But one concrete representation of s is the following operation tree:
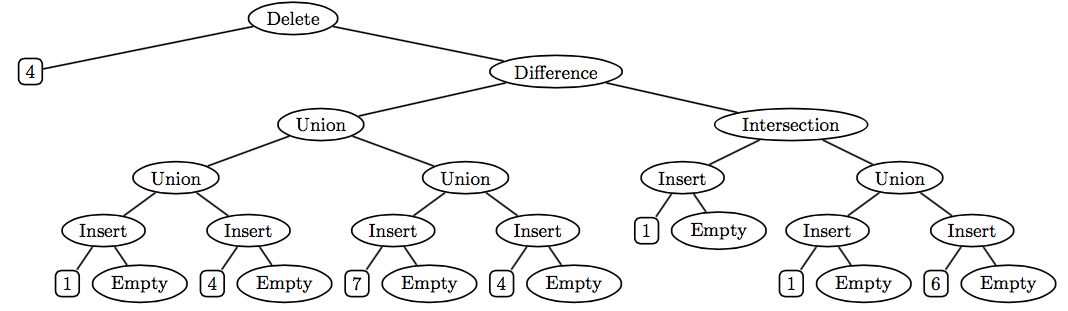
One advantage of using such operation trees to represent sets is that the empty, insert, delete, union, difference, and intersection operations are extremely cheap — they just create a new tree node with the operands as subtrees, and thus take constant time and space! But other operations, such as member and toList, can be more expensive than in other implementations.
In this problem, you are asked to flesh out the missing operations in the skeleton of the OperationTreeSet structure shown below. Your ~wx/cs251/sml/ps7 folder contains the starter file OperationTreeSet.sml. When you finish this problem, rename the file to yourAccountName-OperationTreeSet.sml before you submit it.
structure OperationTreeSet :> SET = struct
datatype ''a t = Empty
| Insert of ''a * ''a t
| Delete of ''a * ''a t
| Union of ''a t * ''a t
| Intersection of ''a t * ''a t
| Difference of ''a t * ''a t
val empty = Empty
fun insert x s = Insert(x,s)
fun singleton x = Insert(x, Empty)
fun delete x s = Delete(x, s)
fun union s1 s2 = Union(s1,s2)
fun intersection s1 s2 = Intersection(s1,s2)
fun difference s1 s2 = Difference(s1,s2)
fun member _ _ = raise Unimplemented
fun toList _ = raise Unimplemented
fun isEmpty _ = raise Unimplemented
fun size _ = raise Unimplemented
fun toPred _ = raise Unimplemented
fun toString eltToString _ = raise Unimplemented
fun fromList _ = raise Unimplemented
fun fromPred _ = raise Unimplementable
endIn the OperationTreeSet structure, the set datatype t is create by constructors Empty, Insert, Delete, Union, Intersection, and Difference. The empty, singleton, insert, delete, union, intersection, difference operations are easy and have been implemented for you. You are responsible for fleshing out the definitions of the member, toList, size, isEmpty, toPred, toString, and fromList operations.
Notes:
-
Your implementation of
membershould not use thetoListfunction. Instead, it should be defined by case analysis on the structure of the operation tree. -
Your
toListfunction should also be defined by case analysis on the structure of the operation tree. Thememberfunction should not be used in the implementation oftoList(because it can be very inefficient). Keep in mind that sets are unordered, and yourtoListfunction may return lists of elements in any order, but it should not have any duplicates. -
In your
toListdefinition, be very careful with includingtoListinside functional arguments, because this can often cause the same list to be calculated a tremendous number of times, leading to tests that take a very long time for large sets. If some of the test cases for large sets don’t return in a reasonable time, this is probably the cause. -
Your implementation of
sizeandisEmptyshould use thetoListfunction. Indeed, it is difficult to implement these functions by a direct case analysis on the operation tree. Note thatsizewill only work correcty if the output oftoListdoes not contain duplicates. -
In the implementation of
toString, the functionString.concatWithis particularly useful. -
In the implementation of
fromList, for lists with >= 2 elements, you should first split the list into two (nearly) equal-length sublists usingList.takeandList.dropand union the results of turning the sublists into sets. This yields a height-balanced operation tree. -
OperationTreeSet.smlends with two collections of test cases. The first collection involves “small” sets that are defined without usingfromList. The second collection involves “big” sets that are defined usingfromList. The expected outputs to these tests can be found in this transcript file. Because of the way the testing functions are written, the integer elements in the outputs formemberandtoPredwill be in sorted order from low to high, but the integers in the outputs fortoListandtoStringmay be in any order. -
The testing code for most functions (all except for
memberand assumes thattoListworks correctly. So you must implementtoListfor for most of the tests to work.
Extra Credit: 2-3 Tree Deletion (20 points)
In SML, implement and test the 2-3 tree deletion algorithm presented in pages 8 through 11 of the handout on 2-3 trees.
Extra Credit: 2-3 Trees in Java (35 points)
Implement and test 2-3 tree insertion and deletion in Java. Compare the SML and Java implementations. Which features of which languages make the implementation easier and why?