• Clarifications shown in magenta.

  • Dueish:: Mon Nov 02

  • Notes:
    • As with all psets, you can work on this problem in a two-person team or as an individual. But you need to partner in a team on at least 3 psets during the semester.
    • You can do Problems 1 through 3 right away.
    • Problems 4 and 5 require only a little knowledge of Racket and some review of CS111-style Divide/Conquer/Glue fruitful recursive functions (see link to CS111 recursion lecture in Problem 5).
    • You should wait until the lectures on big-step and small-step semantics before attempting Problem 6.
    • The problems needn’t be done in order. Feel free to jump around.
    • This pset has 100 points, but also includes a competely optional 12-point extra credit problem. You should only attempt the extra credit problem once you have finished the required problems. Extra credit problems must always be done by individuals, never by a team.

  • How to Start PS1

    1. Follow the instructions in the GDoc CS251-F20-T2 Pset Submission Instructions for creating a PS1 Google Doc. Put all written answers and a copy of all code into this PS1 GDoc.

    2. Create a file folder on your computer named yourCSAccountName_ps1 (e.g., gdome_ps1). (If working on a two-person team, you can use one partner’s name or combine both partners names.) Below you will be asked to populate this file folder with various files on the assignment that you will submit (in the final step) to a drop folder on cs.wellesley.edu.

  • Submission:

    • For all problems, include all answers (including Racket code and big-step/small-step derivations) in your PS1 GDoc. Please format your Racket function definitions in Problem 5 and your derivations in Problem 6 so that they’re easy to read. Format all derivations and code using a fixed-width font (Courier New or Consolas). You use a small font size if that helps.

    • For Problem 1 (Concrete Syntax), put your updateScore.py and updateScore.js files in your yourCSAccountName_ps1 folder on your computer.

    • For Problem 5 (Racket Recursion), put your ps1-functions.rkt file in your yourCSAccountName_ps1 folder on your computer.

    • Drop a copy of your yourCSAccountName_ps1 folder into your ~/cs251/drop/ps01 drop folder on cs.wellesley.edu (a.k.a. tempest). For transferring files to your CS251 drop folder, you may use a file transfer application like Cyberduck, but you can also use scp from a Terminal window on your computer via the following command. (This assumes you are connected to the correct directory and have replaced both occurrences of gdome by your tempest username.)

      ~~~ scp -r yourCSAccountName_ps1 gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps01 ~~~

1. Concrete Syntax (18 points)

This problem explores how the same program can be written with different concrete syntax in different languages.

Consider the following App Inventor program, which consists of two global variable declarations and the declaration of an updateScore procedure. (This program is incomplete, since updateScore is never called.)

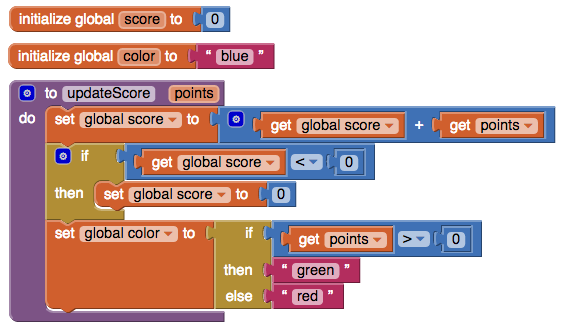
App Inventor updateScore procedure example

Create two files, updateScore.py and updateScore.js, that contain, respectively, (1) Python and (2) JavaScript versions of this App Inventor program. These files must also include (1) testing code that shows the programs work as expected and (2) transcripts showing the result of running the test cases (as comments in the code).

Notes:

  • If you don’t know or can’t remember details of Python or JavaScript syntax, look it up on the Web!

  • The App Inventor example includes two global variable declarations (score and color), a local procedure parameter declaration (points), variable references (getters) for all of these, and variable assignments (setters) for the global variables. In one of your programs, you will need an extra declaration to distinguish global from local variables. Why? (You don’t need to answer this question in your solution, but should think about it.)

  • You should translate App Inventor’s get block as a simple variable reference. E.g. get x in App Inventor would translate to the variable reference x in both languages.

  • You should translate App Inventor’s set block as a simple variable assignment. E.g. set x 42 would translate to x = 42 in both languages.

  • App Inventor includes both conditional statement blocks (the two left blocks below) and conditional expression blocks (the rightmost block below). Make sure you understand the difference between these and translate them appropriately.

    App Inventor conditional blocks

    In general, a statement is a program phrase that performs an action while an expression is a program phrase that returns a value. In App Inventor, statements compose vertically to emphasize that their actions are performed sequentially from top to bottom, while expressions have plugs on their left side that denote the value returned by the expression. This value is used by the block whose socket the plug is connected to.

    Both Python and JavaScript have different syntax for conditional statements vs. conditional expressions. In your programs, you should use the appropriate syntax for each one. (If you don’t know it, look it up!) In particular, do not use the conditional statement syntax to translate App Inventor’s conditional expression block!

  • What App Inventor calls a “procedure” is called a “function” in Python and JavaScript. The term “function” often implies that callers for the entity can return a value (i.e., function calls are expressions), whereas “procedure” often implies that callers for the entity perform an action but do not return a value (i.e., procedure calls are statements). But the usage is rather inconsistent between languages.

  • You must test your updateScore functions to verify that they work correctly. E.g., you can use a Python intepreter to test updateScore.py and a JavaScript interpreter in the browser (or a standalone Node.js JavaScript intepreter) to test updateScore.js. You should show the inputs and outputs of all test cases. For full credit, you should use test cases that exercise all combinations of conditional branches in your updateScore functions.

  • In your testing, you need only consider inputs that are numbers. Don’t worry how the functions deal with non-numeric inputs.

BTW #1: App Inventor also has top-level declarations (blocks that introduce top-level named entities, like procedures and global variables). These are blocks that do not have any plugs or sockets and so cannot be connected to other blocks.

BTW #2: Racket only has declarations and expressions; it does not have statements. So Racket’s if is a condtional expression and not a conditional statement. What’s it like to program in a language without statements? You’ll find out!

BTW #3: If you’re curious, you can learn more about App Inventor at the MIT App Inventor website and can experiment with building your own apps using the App Inventor development environment. You can even test your new apps on your own mobile device using the MIT AI2 Companion app:

  • If you have an Android device, you can test the apps you create on your device by downloading the MIT AI2 Companion from the Google Play Store on that device.

  • If you have an iOS device, there is a beta version of the Companion you can test. First you need to install the TestFlight app from the Apple app store on you device. Then go to this link on your device’s browser after installing TestFlight. This will download and install the iOS companion on your device.

2. The Evils of Two Lesses (15 points)

Consider the exact expression (3 < 4 < 2). (Do not remove the parens or any spaces, add any extra parens, or move around any symbols.) This expression is handled differently in different programming languages. For each of the following four programming languages, explain how this expression is handled in that language.

  • If the expression returns a value, specify that value and explain why that value is returned and how you know this fact. Give evidence from a sample program in that language that is has the value you claim. Your explanation can’t just be ``This is the value the interpreter for the language returned”. You have to explain why this particular value is returned according to the evaluation rules of the language.

  • If the expression causes an error, explain the nature of the error (is it a syntax error? static type error? dynamic type error? something else?) and how you know this fact. Again, give evidence from a sample program in that language that is has the error you claim.

  1. Java (4 points)
  2. JavaScript (4 points)
  3. Python (4 points)
  4. Racket (3 points)

Note: If the answer depends on special features of the language, you should cite a source for the documentation explaining those features.

3. Truthiness (16 points)

truthiness image)

In the context of a conditional test, a value that chooses the then arm of the conditional is called truthy and a value that chooses the else arm of the conditional is called falsey (sometimes spelled falsy). We will use the term neither to refer to a value that cannot be used as a conditional test (causing a compile-time or run-time error).

We have seen that in Racket, the #f value is falsey and every value that is not #f is truthy; Racket has no neither values. This problem asks you to explore truthiness in other languages.

Below are five programming languages and links to their language specification documents. Based on information in the documents, determine which values are truthy, which are falsey, and which (if any) are neither. In your answers, explicitly cite all the sections of the reference manuals that you use to justify your answer. Points will be deducted if appopriate citations are missing.

Notes:

  • Hint: begin by searching for the terms if statement or conditional in the documents.

  • One of the purposes of this problem is to introduce you to language specification documents. These are the authoritative sources for answering any questions about the languages, even nit-picky ones. Although they can be somewhat dense, you should get into the habit of consulting them. For reasons you will understand after doing this problem, people who write/consult/cite such language specifications are sometimes called language lawyers.

  • In the EcmaScript specification, notions like ReturnIfAbrupt and CompletionRecord are used to model the dynamic semantics of exceptions and can be ignored for the purposes of this problem.

  • The correct answer for C is particularly challenging to track down. Consider the following in your answer:

    • The true and false macros defined in Sec 7.18 are not relevant for this problem
    • The C specification for the semantics of if statments uses the terminology “compares equal to 0”. Although it’s not obvious, this terminology is defined in Section 6.5.9 Equality operators on p. 96.
    • The C specification for the semantics of if statements mentions “scalar types”. It’s important to understand what these are and what other types there are in C.
    • The notion of conversion between values of different types (Se 6.3.2) plays a role in this problem.
    • In C, a pointer is an abstraction over a memory address. Are there any pointers treated as falsey?
    • How are arrays treated by C in the context of a test expression? Is there any conversion on arrays that might treat them as a non-neither value?
    • Even after carefully considering all of the above, be warned that the situation may be as clear as mud. Give your best interpretation of the information that you find! <

  • Compare the length of the Scheme reference document (only 50 pages) to the others. When people say that Scheme/Racket are simpler than other languages, this is one piece of evidence that they give.

4. Racket Evaluation (11 points)

For each of the following Racket definitions, write the value to which the variable will be bound. If evaluating the expression in the definition would give rise to an error, write error, along with a brief explanation of why the error occurs.

Write your answers, with one line per definition, in order, in the form:

x |-> 7
y |-> 3
z: error -- attempt to divide a number by 0.

meaning that variable x is bound to value 7, variable y is bound to value 3, and evaluating the binding for z results in a divide-by-zero error.

Predict the answers without running the code. You may find it useful to write evaluation derivations, leaving blanks for the result values as you build the derivation, and then filling in the results once you begin to reach values, but you do not need to submit any derivations in this problem. You may also check your manually evaluated answers by running each binding in order in the DrRacket REPL. (Instructions on using DrRacket are here.) It’s OK to change your answer if the interpreter shows that your predicted answer is incorrect. However, in this case, you should explain that your original prediction was wrong and your understanding of why the answer given by the interpreter is correct.

#lang racket
(define a 5)

(define b (* a a))

(define c (+ (* 2 a) (- b a)))

(define d (+ a b c))

(define e (+ a))

(define f (+))

(define g (*))

(define h b)

(define i (if (< a 0) 7 (quotient 43 a)))

(define j (if (= a 0) 11 (remainder 43 a)))

(define k (/ i j))

(define l (< a b))

(define m (= b c))

(define n (< b c d))

(define o (+ a m))

(define p (< a m) )

(define q (if a b c))

(define r (if l m n))

(define s (if (if (< i j) m l)
              (if (> a c) (+ a c) (* a c))
              (if (< a b) (+ a b) (* a b))))            

(define t (= (if (< b c)
                 (* (remainder (- (* a b) (* 2 a)) c) (- (quotient d b)))
                 (* (- (+ d (* (* a b) (quotient d a))))))
             (- (* (/ (- c a) (- a 1)) (quotient b (if (> a c) i j))))))

(define u (if (> i j) (< a 0) (< (< b c) a)))

(define v (if (<= i j) (< a 0) (< (< b c) a)))

5. Racket Recursion (20 points)

Although you’ve written recursive function definitions before in other courses, recursion is particularly important in CS251 for three reasons:

  • The list data structures in Racket and Standard ML are recursively defined, and so are naturally processed with recursion. (You will get lots of practice with these starting next week.)

  • Neither Racket nor Standard ML has looping constructs, so what you would express via loops in other languages must be expressed via recursion in these languages.

  • Later in the semester we will study metaprograms – i.s., programs that manipulate other programs. Metaprograms typically process the abstract syntax tree (AST) structure of the program being manipulated. Such tree processing is most naturally expressed using recursion. Indeed, you’ve already seen that big-step evaluation semantics is tree-recursive in nature.

For each of the two Racket function specifications below, write and test a recursive function that satisfies that specification. In all of your definitions, you should use the following recursive problem solving strategy:

  • For which argument(s) is the function so simple that the answer can be returned immediately? This is the base case.

  • For the other case(s) (known as the recursive case(s)), use divide/conquer/glue:

    • divide: make one or more subproblems that are smaller instances of the given problem;

    • conquer: assume that the recursive function you’re defining simply works and returns the correct answer on all of the smaller problems.

    • glue: combine the result(s) of the recursive function call(s) with information in the original problem to create the correct result for the whole problem.

Notes:

;; Return the factorial of n
(define fact 
  (lambda (n)
    (if (= n 0)
        1
        (* n (fact (- n 1))))))

;; Return the nth Fibonacci number
(define fib
  (lambda (n)
    (if (<= n 1)
        n
        (+ (fib (- n 1)) (fib (- n 2))))))

;; Return the sum of the integers between lo and hi
(define sum-between
  (lambda (lo hi)
    (if (> lo hi)
        0
        (+ lo (sum-between (+ lo 1) hi)))))

  • For this problem, you should use Dr. Racket to create a single file named yourCSAccountName-ps1-functions.rkt that contains all the functions (including helper functions) that you define for this problem.

  • In your definitions you should not introduce any recursive helper functions. (But you can define nonrecursive helper functions).

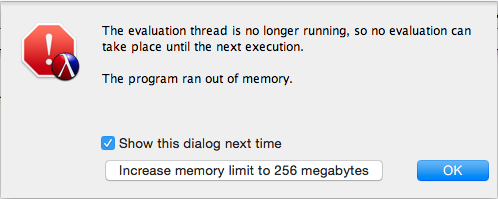
  • If the following error message pops up during the testing of one of your functions, it mostly likely means that you have an infinite recursion that doesn’t reach its base case and runs out of memory due to a stack depth that cannot fit into available memory.

box-and-pointer-diagram

  1. (10 points) Define a function sum-squares-of-ints-divisible-by that takes three integer arguments (divisor, lo, and hi) and returns the sum of the squares of all the integers between lo and hi (inclusive) that are evenly divisible by divisor.

     > (sum-squares-of-ints-divisible-by 2 1 8)
 120 ; =  2^2 + 4^2 + 6^2 + 8^2
 > (sum-squares-of-ints-divisible-by 3 1 10)
 126 ; =  3^2 + 6^2 + 9^2
 > (sum-squares-of-ints-divisible-by 5 1 10)
 125 ; =  5^2 + 10^2 
 > (sum-squares-of-ints-divisible-by 7 1 10)
 49 ; =  7^2 
 > (sum-squares-of-ints-divisible-by 11 1 10)
 0 ; no multiples of 11 between 1 and 10
 > (sum-squares-of-ints-divisible-by 11 7 15)
 121 ; = 11^2
 > (sum-squares-of-ints-divisible-by 2 10 8)
 0 ; the range "from 10 up to 8" is empty

    Use the following helper function in this problem:

    (define divisible-by?
  (lambda (num divisor)
    (= (remainder num divisor) 0)))

    Notes:

    • You may assume that all three inputs are integers. You need not worry about handling or testing inputs that are not integers.

    • Although not shown in the above examples, any of the integer inputs can be negative. So both (sum-squares-of-ints-divisible-by 2 -4 4) and (sum-squares-of-ints-divisible-by -2 -4 4) should yield 40 = (-4)^2 + (-2)^2 + 0^2 + 2^2 + 4^2 and (sum-squares-of-ints-divisible-by 3 -10 -1) should yield 126 = (-9)^2 + (-6)^2 + (-3)^2.

  2. (10 points) A Hamming number is any positive integer expressible as 2i⋅3j⋅5k. E.g., the Hamming numbers between 1 and 100 are:

    1 2 3 4 5 6 8 9 10 12 15 16 18 20 24 25 27 30 32 36 40 45 48 50 54 60 64 72 75 80 81 90 96 100

    Define a function hamming? that takes a single numeric argument (including 0, negatives, and nonintegers), and returns #t if the argument is a Hamming number and #f if it is not. Your function need not work on arguments that are not numbers.

     > (hamming? 30)
 #t
 > (hamming? 31)
 #f
 > (hamming? -31)
 #f
 > (hamming? 3.141)
 #f
 > (hamming? 0)
 #f
 > (filter hamming? (range -100 101)) ; list all integers from -100 up to
                                      ; (but not including) 101 
                                      ; for which hamming? is true
 '(1 2 3 4 5 6 8 9 10 12 15 16 18 20 24 25 27 30 32 36 40 45 48 50 54 60 64 72 75 80 81 90 96 100)

    Notes:

    • As with all recursive functions, use the divide/conquer/glue strategy to solve this one.
    • You may assume that the input is a number. You need not worry about handling or testing inputs that are not numbers.
    • Use integer? to test if a value is an integer.
    • Use (and E1 E2 ... En) to determine if all of the expressions E1, E2, …, En are true.
    • Use (or E1 E2 ... En) to determine if at least one the expressions E1, E2, …, En is true.
    • You needn’t use any if expressions in your definition. All you need are and and or. (But you can use if if you want to.)
    • The divisible-by? helper function from Problem 5a may be useful here as well but is not required. There are correct solutions that do not use divisible-by?.

6. Big-step and Small-step Semantics (20 points)

Lec 04 and Lec 05 introduce two models for evaluation of Racket expressions:

  • The big-step evaluation model shows the evaluation of an expression as an evaluation derivation tree in which the evaluation of the whole expression is determined from the evaluation of its subexpressions.

  • The small-step evaluation model shows the evaluation of an expression as an step-by-step process in which the lefmost redex (reducible expression) is evaluated on each step until there are no more redexes.

As an example, consider evaluating the Racket expression (if (< x y) (* (- y 10) x) (/ y 0)) in an environment env2 in which x is bound to 5 and y is bound to 17. Then one way to write big-step evaluation derivation of this expression is

    | | x # env2 ↓ 5 [varref]
    | | y # env2 ↓ 17 [varref]
    | -------------------- [less-than]
    | (< x y) # env2 ↓ #t 
    | 
    | | | y # env2 ↓ 17 [varref]
    | | | 10 # env2 ↓ 10 [value]
    | | -------------------- [subtraction]
    | | (- y 10) # env2 ↓ 7
    | |
    | | x # env2 ↓ 5 [varref]
    | -------------------------- [multiplication]
    | (* (- y 10) x) # env2 ↓ 35
    ----------------------------------------------- [if nonfalse]
    (if (< x y) (* (- y 10) x) (/ y 0)) # env2 ↓ 35

In the above conclusion-below-subderivations format, each conclusion below a dotted line is justified by the subderivations above the dotted line. Another way to write this derivation is “upside down” using conclusion-above-subderivations format, where each conclusion at the top is justified by the bulleted subderivations below it:

  • (if (< x y) (* (- y 10) x) (/ y 0)) # env2 ↓ 35 [if nonfalse]
    • (< x y) # env2 ↓ #t [less-than]
      • x # env2 ↓ 5 [varref]
      • y # env2 ↓ 17 [varref]
    • (* (- y 10) x) # env2 ↓ 35 [multiplication]
      • (- y 10) # env2 ↓ 7 [subtraction]
        • y # env2 ↓ 17 [varref]
        • 10 # env2 ↓ 10 [value]
      • x # env2 ↓ 5 [varref]

A small-step derivation sequence for this example is shown below. Curly braces have been used to highlight the redex in the expression at each step. Rules names in square brackets show the rule used to reduce the redex in the previous line to the result in the current line.

    (if (< {x} y) (* (- y 10) x) (/ y 0)) # env2 

    ⇒ (if (< 5 {y}) (* (- y 10) x) (/ y 0)) # env2 [varref]

    ⇒ (if {(< 5 17)} (* (- y 10) x) (/ y 0)) # env2 [varref]

    ⇒ {(if #t (* (- y 10) x) (/ y 0))} # env2 [less-than]

    ⇒ (* (- {y} 10) x) # env2 [if nonfalse]

    ⇒ (* {(- 17 10)} x) # env2 [varref]

    ⇒ (* 7 {x}) # env2 [subtraction]

    ⇒ {(* 7 5)} # env2 [varref]

    ⇒ 35 # env2 [multiplication]

Despite differences between the big-step and small-step derivations, both are ultimately describing the same evaluation process, so they share lots of similarities:

  • They evaulate the same subexpressions to the same values and get the same final result value for the whole expression.
  • In both derivations, only the “then” clause of the if expression is evaluated. This is a good thing, since evaluating the “else” clause (/ y 0) would give a division-by-zero error.

a. Big-step derivation (12 points)

Construct a big-step derivation for the following expression in an environment env5 with bindings a↦3, b↦6, c↦4:

(+ (if (< a b) (* a (+ b c)) (+ b #t))
   (if (if (> a c) (< c b) (- c 4)) (* 2 b) a))

You may use either the conclusion-below-subderivations format or conclusions-above-subderivation format shown above — whichever you prefer. Regardless of format, you should indicate in brackets which rule is being used at each step of the derivation.

b. Small-step derivation (8 points)

Construct a small-step derivation for the same expression as in part a in the same environment, using the same formatting conventions used in the small-step derivation example above. In particular:

  • Each step of the small-derivation should evaluate the leftmost redex, which should be highlighted between curly braces.
  • The result of each step should be annotated with the rule name (in curly braces) used to reduce the redex from the previous line.

Extra Credit: Distinguishing Languages with One Expression (10 points)

This problem is optional. You should only attempt it after completing all the other problems.

In Problem 3, you saw that Racket, Python, JavaScript, and C all have slightly different notions of truthy and falsey. In this problem, the goal is to use this fact to design a single expression that denotes a string, and the string it denotes names the language in which the string is evaluated.

Of course, each of these four languages has a different syntax, so the “single expression” can’t be exactly the same in all the languages. Rather, it should have the same abstract syntax in all the languages but the concrete syntax can differ.

For example, consider these two conditional expressions:

  • JavaScript: ((3 < 4 < 2) ? "javascript" : "python")
  • Python: "javascript" if 3 < 4 < 2 else "python"

They have different concrete syntax but the same abstract syntax. (Actually, (3 < 4 < 2) is treated slightly differently in terms of abstract syntax trees in JavaScript and Pyton, but let’s ignore this detail for now.) But because of the difference in senantics between the languages, the JavScript expression evaluates to "javascript" and the Python expression evaluates to "python".

Your goal is to write a single (abstract syntax) expression that can return one of the four strings "javascript", "python", "racket" or "c", and when the (concrete syntax) of this expression is evaluated in JavaScript, Python, Racket, or C, it returns the name of the language in which it was evaluated. So effectively this expression is a test that answers the question “Which language I am in?”.

Notes:

  • You should give the concrete syntax of the same abstract expression in all four languages, and show a transcript from all four languages that it has the desired behavior.

  • You are allowed to use the following syntactic elements in your expression: numbers, strings, lists/arrays, and conditional expressions. You are not allowed to use operators (such as +, <, etc.) or built-in functions. Because of the restriction on <, you cannot use the example above to distinguish JavaScript and Python.

  • For the purposes of this problem, Racket’s immutable lists, Python’s & JavaScript’s mutable lists, and C’s arrays will be considered “equivalent”. E.g. Racket’s list '(1 2 3), Python’s & JavaScript’s list [1, 2, 3], and C’s array {1, 2, 3} will be considered “the same”.

  • For the C expression, you may (1) declare arrays outside of the expression that are used inside the expression and (2) may use explicit type casts to cast arrays to a type suitable for truthy/falsey.

  • You can get partial credit for distinquishing a subset of the languages: 2 points for distinquishing two languages, 5 points for distinguishin three languages, and 10 points for distinguishing all four.