CS 251: OPTIONAL: Open to Interpretation

Dueish: Fri. Dec. 18. (But keep in mind that all work will be accepted through Sat. Jan 02.)
Notes:
- This problem set is completely optional.
- This pset has three regular problems worth 91 total points. It also has two extra credit problems worth 40 total points.
- Unlike other extra credit problems, you may do the regular problems of this pset with a partner. These are the only problems in the course on which you may earn extra points with a partner.
  - However, make sure that you and you partner have compatible expectations on when you plan to complete the work on these probelms. Some may wish to be done by Dec. 18, and others before the holidays. It is less likely that partners may wish to work through the holidays.
- Any points you earn on the regular (not labeled as extra credit) problems of this assignment will count as extra points toward the pset component of your grade but will not count toward the 50 point extra credit limit on extra credit points mentioned in the syllabus.
  - In contrast, the two problems labeled extra credit will count toward the 50-point extra credit limit. Also, the problems labeled extra credit must be done individually.
- Of course, partial credit will be awarded where appropriate for incomplete problems.

Times from some previous semesters (in hours)

Times	Problem 1	Problem 2	Problem 3	Total
average time (hours)	2.1	3.2	2.3	8.6
median time (hours)	2.0	3.0	2.0	8.0
25% took more than	3.0	4	2.75	9.75
10% took more than	3.9	4	3.5	11.4

How to Start PS7
- Follow the instructions in the GDoc CS251-F20-T2 Pset Submission Instructions for creating your PS7 Google Doc. Put all written answers and a copy of all code into this PS7 GDoc. If you are working with a partner, only one of you needs to create this document, but you should link it from both of your List Docs.
Submission:
- For all parts of all problems, include all answers (including SML code and metalanguage derivatations) in your PS7 google doc. Format SML code using a fixed-width font, like Consolas or Courier New. You can use a small font size if that helps. o
- For Problem 1:
  - Include all new/modified functions from your file yourAccountName-BindexToPostFix.sml in your GDoc (so that the graders can comment on them). In the GDoc, you need only include your new and modified unctions, not all of the code of all the files you edited!
  - Drop a copy of your ~/cs251/sml/ps6/yourAccountName-BindexToPostFix.sml file in your ~/cs251/drop/ps07 drop folder on cs.wellesley.edu by executing the following (replacing all three occurrences of gdome by your cs server username):
```
scp -r ~/cs251/sml/ps7/gdome-BindexToPostFix.sml gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps07
```
- For Problem 2:
  - Include all new/modified functions from your files yourAccountName-Simprex.sml and yourAccountName-SimprexEnvInterp.sml in your GDoc (so that the graders can comment on them). In the GDoc, you need only include your new and modified unctions, not all of the code of all the files you edited!
  - Drop a copy of your ~/cs251/sml/ps6/yourAccountName-BindexToPostFix.sml file in your ~/cs251/drop/ps07 drop folder on cs.wellesley.edu by executing the following (replacing all three occurrences of gdome by your cs server username):
```
scp -r ~/cs251/sml/ps7/gdome-Simprex.sml gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps07
scp -r ~/cs251/sml/ps7/gdome-SimprexEnvInterp.sml gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps07
```
- For Problem 3, include your interpretation/compilation derivations. It is easiest to write these top-down via nested bullets, as shown in both the pset description and the lecture notes.

Starting this Problem Set

All coding parts in Problems 1 and 2 involve starter files in the ~/cs251/sml/ps7 directory in your csenv Virtual Machine.

To create this directory, execute this Linux commands in a shell on your csenv appliance:

cd ~/cs251/sml
git pull origin master

If you encounter any issues when executing these commands, you can troubleshoot by following these git instructions. If these instructions don’t help, please contact Lyn.

REMINDER: ALWAYS MAKE A BACKUP OF YOUR .sml FILES AT THE END OF EACH DAY TO AVOID POTENTIAL LOSS OF WORK.

1. Bindex To PostFix (22 points)

Background

In Lec 32, we studied the following intexToPostFix function that automatically translates Intex programs to equivalent PostFix programs:

fun intexToPostFix (Intex.Intex(numargs, exp)) =
  PostFix.PostFix(numargs, expToCmds exp 0)
    (* 0 is a depth argument that statically tracks 
       how many values are on stack above the arguments *)

and expToCmds (Intex.Int i) depth = [PostFix.Int i]
  | expToCmds (Intex.Arg index) depth = [PostFix.Int (index + depth), PostFix.Nget]
   (* specified argument is on stack at index + depth *)
  | expToCmds (Intex.BinApp(binop,exp1,exp2)) depth =
    (expToCmds exp1 depth) (* 1st operand is at same depth as whole binapp *)
    @ (expToCmds exp2 (depth + 1)) (* for 2nd operand, add 1 to depth 
                                      to account for 1st operand *)
    @ [PostFix.Arithop (binopToArithop binop)]

and binopToArithop Intex.Add = PostFix.Add
  | binopToArithop Intex.Sub = PostFix.Sub
  | binopToArithop Intex.Mul = PostFix.Mul
  | binopToArithop Intex.Div = PostFix.Div
  | binopToArithop Intex.Rem = PostFix.Rem

For example, given the Intex program intexP2 expressed as an Intex.pgm datatype instance

val intexP2 = Intex(4, BinApp(Mul,
                              BinApp(Sub, Arg 1, Arg 2),
                              BinApp(Div, Arg 3, Arg 4)))

the intexToPostFix translation is as follows:

- intexToPostFix(intexP2);
val it =
  PostFix
    (4,
     [Int 1,Nget,Int 3,Nget,Arithop Sub,Int 4,Nget,Int 6,Nget,Arithop Div,
      Arithop Mul]) : PostFix.pgm

With the helper function translateString shown below, the input and output of translation can be expressed as strings in s-expression format:

fun translateString intexPgmString =
  PostFix.pgmToString (intexToPostFix (Intex.stringToPgm intexPgmString))

- IntexToPostFix.translateString("(intex 4 (* (- ($ 1) ($ 2)) (/ ($ 3) ($ 4))))");
val it = "(postfix 4 1 nget 3 nget sub 4 nget 6 nget div mul)" : string

There are two key aspects to the translation from Intex to PostFix:

The expToCmds function translates every Intex expression to a sequence of PostFix commands that, when executed, will push the integer value of that expression onto the stack. In the case of translating a binary application expression, this sequence is composed by appending the sequences for the two operands followed by the appropriate arithmetic operator command.
The trickiest part of expToCommands is knowing how many integers are on the stack above the program arguments, so that references to Intex arguments by index can be appropriately translated. This is handled by a depth argument to expToCommands that keeps track of this number. Note that the first operand of a binary application has the same depth as the whole binary application expression, but the second operand has a depth one greater than the first to account for the integer value of the first operand pushed onto the stack.

Your Task

In this problem, you will think about and implement a similar translator from Bindex programs to PostFix programs.

Hand translating a sample Bindex expression (8 points) To get a better sense for the issues involved, give the PostFix program (in s-expression notation) that results from translating by hand the following Bindex program:
```
(bindex (a b)
  (- (bind c (+ a b)
       (+ (bind d (/ c a)
            (* (+ d b)
               (- a d)))
          (* b c)))
     (* b a)))
```
As in the the Intex-to-PostFix translator studied in class, your translation should have the following properties:
- The operands of an operator should be translated from left to right.
- When the commands translated from an expression are executed on a stack of values, they should have the effect of pushing onto the stack a single value that is the value of that expression. No other changes should be made to the original stack other than pushing this single value.
- The original program arguments should never be removed from the stack; they should always be the bottommost values on the stack.
- The value introduce by a bind should be pushed onto the stack before the body is evaluated and not popped until after the value of the body has been determined.
- You should not perform any clever optimizations in your translation. The purpose of this problem is to give you insight into how the translation can be performed automatically without any cleverness.
Your are required to comment the PostFix code that results from your translation to explain how it corresponds to parts of the original Bindex program.

Run your resulting program in PostFix to verify that it works as expected. In particular, running the PostFix program that results from hand translating the above Bindex program on the arguments 2 6 should return 16. If it doesn’t, there’s a bug in your translation strategy.

Fleshing out the translator (14 points): The file ps7/BindexToPostFix.sml contains a skeleton of the Bindex to PostFix translator in which all Bindex expressions translate to a command sequence consisting of the single integer command 42:

fun makeArgEnv args = Env.make args (Utils.range 1 ((length args) + 1))
(* returned env associates each arg name with its 1-based index *)

fun envPushAll env = Env.map (fn index => index + 1) env
(* add one to the index for each name in env *)

fun envPush name env = Env.bind name 1 (envPushAll env)

fun bindexToPostFix (Bindex.Bindex(args, body)) =
  PostFix.PostFix(length args, expToCmds body (makeArgEnv args))

(* In expToCmds, env statically tracks the depth of each named variable
   value on the stack *)
and expToCmds (Bindex.Int i) env = [PostFix.Int 42] (* replace this stub *)
  | expToCmds (Bindex.Var name) env = [PostFix.Int 42] (* replace this stub *)
  | expToCmds (Bindex.BinApp(binop, rand1, rand2)) env = [PostFix.Int 42] (* replace this stub *)
  | expToCmds (Bindex.Bind(name, defn, body)) env = [PostFix.Int 42] (* replace this stub *)

and binopToArithop Bindex.Add = PostFix.Add
  | binopToArithop Bindex.Sub = PostFix.Sub
  | binopToArithop Bindex.Mul = PostFix.Mul
  | binopToArithop Bindex.Div = PostFix.Div
  | binopToArithop Bindex.Rem = PostFix.Rem

Begin this part by renaming the file BindexToPostFix.sml to be yourAccountName-BindexToPostFix.sml.

When this file is loaded, evaluating the expression testAll() will run the translator on a collection of test cases. Initially, all of these test cases will fail. Your task is to redefine the clauses of expToCmds so that all the test cases succeed.

Notes:

The expToCmds function in the Bindex to PostFix translator uses an environment to track the depth of each variable name in the program. Recall from Lec 33hat an environment (defined by the Env structure in utils/Env.sml) maps names to values. In this case, it maps names in a Bindex program to the current stack depth of the value associated with that name. Carefully study the helper functions makeArgEnv, envPushAll, and envPush to understand what they do; all are helpful in the contex of this problem.
As in the Intex to PostFix translator, in the Bindex to PostFix translator, each Bindex expression should translate to a sequence of PostFix commands that, when executed, pushes exactly one value — the integer value of that expression — onto the stack. More formally, translating a Bindex expression to PostFix should obey the following invariant:

A Bindex expression E should translate to a sequence of commands, that, when executed on a stack S, should result in a stack v :: S, where v is the result of evaluating E relative to an environment represented by S.
For simplicity, you may assume there are no unbound variables in the Bindex program you are translating. With this assumption, you may use the Option.valOf function to extract the value v from a SOME(v) value.

The BindexToPostFix structure contains a testTranslator function that takes the name of a file containing a Bindex program and a list of argument lists and (1) displays the Bindex program as an s-expression string, (2) displays the PostFix program resulting from the translation as an s-expression string and (3) tests the behavior of both programs on each of the argument lists in the list of argument lists. If the behaviors match, it prints an approprate message; if they don’t match, it reports an an error with the two different result values. For instance, in the initial skelton, the behavioral tests fail on the program in ../bindex/avg.bdx:

Testing Bindex program file ../bindex/avg.bdx

Bindex program input to translation:
(bindex (a b) (/ (+ a b) 2))

PostFix program output of translation:
(postfix 2 42)

Testing args [3,7]: *** ERROR IN TRANSLATION ***
  Bindex result: 5
  PostFix result: 42

Testing args [15,5]: *** ERROR IN TRANSLATION ***
  Bindex result: 10
  PostFix result: 42

However, when the translator is working, the following will be displayed:

Testing Bindex program file ../bindex/avg.bdx

Bindex program input to translation:
(bindex (a b) (/ (+ a b) 2))

PostFix program output of translation:
(postfix 2 1 nget 3 nget add 2 div)

Testing args [3,7]: both programs return 5

Testing args [15,5]: both programs return 10

The function BindexToPostFix.testAll() runs a suite of test cases. You have succeeded when all of the test cases succeed when you evaluate this expression.
If some test cases succeed but others fail, it is likely that you are not obeying the invariant mentioned above. Think about this invariant carefully!

2. Simprex (37 points)

Background

Rae Q. Cerf of Toy-Languages-я-Us likes the sigma construct from the Bindex lecture, but she wants something more general. In addition to expressing sums, she would also like to express numeric functions like factorial and exponentiation that are easily definable via simple recursion. The functions that Rae wants to define all have the following form:

f(n) = z, if n ≤ 0
f(n) = c(n, f(n-1)), if n > 0

Here, z is an integer that defines the value of f for any non-positive integer value and and c is a binary combining function that combines n and the value of f(n−1) for any positive n. Expanding the definition yields:

f(n) = c(n, c(n-1, c(n−2, ... c(2, c(1, z)))))

For example, to define the factorial function, Rae uses:

z_fact = 1
c_fact(i, a) = i*a

To define the exponentation function bⁿ, Rae uses:

z_expt = 1
c_expt(i, a) = b*a

In this case, c_expt ignores its first argument, but the fact that c_expt is called n times is important.

As another example, Rae defines the sum of the squares of the integers between 1 and n using

z_sos = 0
c_sos(i, a) = (i*i) + a

The examples considered so far don’t distinguish right-to-left vs. left-to-right evaluation, A simple example of that is

z_sub = 0
c_sub(i, a) = i-a

For example, when n is 4, the result is the value of 4 - (3 - (2 - (1 - 0))), which is 2, and not the value of 1 - (2 - (3 - (4 - 0))), which is -2.

Another example that distinguishes right-to-left vs. left-to-right evaluation is using Horner’s method to calculate the value of the polynomial x^(n-1) + 2*(x^(n-2)) + 3*(x^(n-3)) + ... + (n-1)*x + n:

z_horner = 0
c_horner(i, a) = i + x*a

For example, when n is 4 and x is 5, the result is (4 + 5*(3 + 5*(2 + 5*(1 + 5*0)))) = 194, which is the value of 5^3 + 2*5^2 + 3*5^1 + 4 = (125 + 50 + 15 + 4) = 194.

Rae designs an extension to Bindex named Simprex that adds a new simprec construct for expressing her simple recursions:

(simprec E_zero (Id_num Id_ans E_combine) E_arg)

This simprec expression evaluates E_arg to the integer value n_arg and E_zero to the integer value n_zero. If n_arg ≤ 0, it returns n_zero. Otherwise, it returns the value

c(n_arg, c(n_arg−1, c(n_arg−2, ... c(2, c(1, nzero)))))

where c is the binary combining function specified by (Id_num Id_ans E_combine). This denotes a two-argument function whose two formal parameters are named Id_num and Id_ans and whose body is E_combine. The Id_num parameter ranges over the numbers from n_arg down to 1, while the Id_ans parameter ranges over the answers built up by c starting at n_zero. The scope of Id_num and Id_ans includes only E_combine; it does not include E_zero or E_arg.

Here is a diagram illustrating the semantics of (simprec E_zero (Id_num Id_ans E_combine) E_arg), in which V_zero is the value of E_zero and V_arg is the value of E_arg:

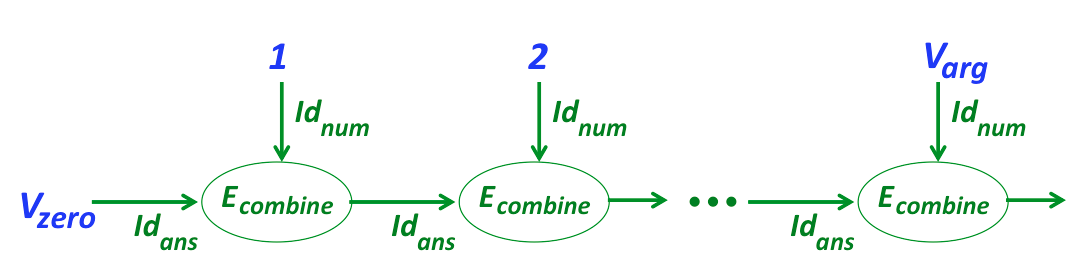
simprec semantics diagram

Note that simprec is effectively performing a foldl on the list [1, 2, 3, ..., V_arg] starting with initial value V_zero using a combiner that would be expressed in Racket as (lambda (Id_num Id_ans) E_combine). Since Bindex does not have any functions (inluduing anonymous higher-order functions introduced by lambda), it is necessary to introduce a new simprec construct in which (Id_num Id_ans E_combine) effectively acts like Racket’s (lambda (Id_num Id_ans) E_combine).

Rae’s simprec expression is closely related to the notion of primitive recursive functions defined in the theory of computation.

Here are some sample Simprex programs along with associated diagrams:

;; Program that calculuates the factorial of n
(simprex (n) (simprec 1 (i a (* i a)) n))

simprec semantics diagram

;; Exponentiation program raising base b to power p 
(simprex (b p) (simprec 1 (i ans (* b ans)) p))

simprec semantics diagram

;; Program summing the squares of the numbers from 1 to hi
(simprex (hi) (simprec 0 (i sumSoFar (+ (* i i) sumSoFar)) hi))

simprec semantics diagram

;; Program distingishing right-to-left and left-to-right evaluation via subtraction
(simprex (n) (simprec 0 (i ans (- i ans)) n))

simprec semantics diagram

;; Calculating x^(n-1) + 2*(x^(n-2)) + 3*(x^(n-3)) + ... + (n-1)*x + n via Horner's method
(simprex (n x) (simprec 0 (i a (+ i (* x a)) n)))

simprec semantics diagram

Your Tasks

After completing her design, Rae is called away to work on another language design problem. Toy-Languages-я-Us is impressed with your CS251 background, and has hired you to implement the Simprex language, starting with a version of the Sigmex implementation. (Sigmex is the name of the language that results from extending Bindex with the sigma construct from lecture.) Your first week on the job, you are asked to complete the following tasks that Rae has specified in a memo she has written about finishing her project.

(18 points) Rae’s memo contains the following Simprex test programs. Give the results of running each of the programs on the argument 3. Show your work so that you may get partial credit if your answer is incorrect.

;; program 1 (2 points)
(simprex (a) (simprec 0 (b c (+ 2 c)) a))

;; program 2 (3 points)
(simprex (x) (simprec 0 (n sum (+ n (* x sum))) 4))

;; program 3 (4 points)
(simprex (y) (simprec 0 (a b (+ b (sigma c 1 a (* a c)))) y))

;; program 4 (9 points)
(simprex (n) 
  (simprec (simprec (* n (- n 3)) (q r r) (* n n))
           (c d (+ d (simprec 0 (x sum (+ sum (- (* 2 x) 1))) c))) 
           (simprec -5 (a b (+ 1 b)) (* n n))))

(19 points)

Rae has created a skeleton implementation of Simprex by modifying the files for the Sigmex (= Bindex + sigma) implementation to contain stubs for the simprec construct. Her modified files, which are named Simprex.sml and SimprexEnvInterp.sml, can be found in the ps7 folder.

Finish Rae’s implementation of the Simprex language by completing the following four tasks, which Rae has listed in her memo:
1. (2 points) Extend the definition of sexpToExp in Simprex.sml to correctly parse simprec expressions.
2. (2 points) Extend the definition of expToSexp in Simprex.sml to correctly unparse simprec expressions.
3. (3 points) Extend the definition of freeVarsExp in Simprex.sml to correctly determine the free variables of a simprec expression.
4. (12 points) Extend the definition of eval in SimprexEnvInterp.sml to correctly evaluate simprec expressions using the environment model.
Notes:
- Begin this part by renaming the files Simprex.sml and SimprexEnvInterp.sml to be yourAccountName-Simprex.sml and yourAccountName-SimprexEnvInterp.sml. In the file yourAccountName-SimprexEnvInterp.sml, you also need to change the first line of the file from
```
use "../ps7/Simprex.sml";
```
  to
```
use "../ps7/yourAccountName-Simprex.sml";
```
- This problem is similar the the Sigmex (= Bindex + sigma) language extension mentioned in the Bindex slides for Lectures 32 and 33. (But we did not discuss Sigmex in class this term.) You are encouraged to study the solution files bindex/Sigmex.sml and bindex/SigmexEnvInterp.sml as part of doing this problem.
- In Simprex.sml, the exp type is defined to be:
```
and exp = Int of int (* integer literal with value *)
        | Var of var (* variable reference *)
        | BinApp of binop * exp * exp (* binary operator application with rator, rands *)
        | Bind of var * exp * exp (* bind name to value of defn in body *)
        | Sigma of var * exp * exp * exp (* E_lo, E_hi, E_body *)
        | Simprec of exp * var * var * exp * exp 
                     (* zeroExp * numVar * ansVar * combExp * argExp *)
```
  The s-expression notation (simprec E_zero (I_num I_ans E_combine) E_arg) is represented in SML as
```
Simprec (<exp for E-zero>, <string for I_num>, <string for I_ans>, 
         <exp for E_combine>, <exp for E_arg>)
```
  For example, the expression (simprec 1 (x a (* x a)) n) is represented in SML as Simprec(Int 1, "x", "a", BinApp(Mul, Var "x", Var "a"), Var "n")
- You can test your modifications of sexpToExp, expToSexp, and freeVarsExp by loading yourAccountName-Simprex.sml into the *sml* buffer, and evaluating the expression Simprex.testSyntax();. This will display the results of various test cases for freeVarsExp, and indirectly will also test sexpToExp and expToSexp. Until sexpToExp is correctly defined, evaluating Simprex.testSyntax(); will raise uncaught exception SyntaxError.
- A common error in this problem is to neglect the nested parens in (Id_num Id_ans E_combine) when defining sexpToExp and expToSexp. For example, the factorial of 5 is calculated by (simprec 1 (i ans (* i ans)) 5), but (simprec 1 i ans (* i ans) 5) (without the nested parens around (i ans (* i ans)) would be a syntax error.
  
  Another way to think of this is as follows. Let’s study the structure of the Sexp instance created by Simprex.stringToSexp "(simprec 1 (i ans (* i ans)) 5)":
```
- Control.Print.printDepth := 100; (* change printDepth to show all details *)
... lots of printout omitted ...
val it = () : unit

- Simprex.stringToSexp "(simprec 1 (i ans (* i ans)) 5)";
val it =
  Seq
    [Sym "simprec",Int 1,
     Seq [Sym "i",Sym "ans",Seq [Sym "*",Sym "i",Sym "ans"]],Int 5] : sexp
```
  Every parenthesized unit in a string representation of an s-expression is converted to a Seq (really Sexp.Seq) with a list of values of type sexp. The list for (simprec 1 (i ans (* i ans)) 5) has four elements: one for each of the four components simprec, 1, (i ans (* i ans)) and 5. The third component is itself a list of the three elements i, ans, and (* i ans).
  
  Suppose you attempt to use the pattern Seq [Sym "simprec", ezero, Sym idnum, Sym idans, ecombine, earg] to match the Seq returned by Simprex.stringToSexp "(simprec 1 (i ans (* i ans)) 5)". This match will fail because the Seq pattern has 6 components and the Seq value it is matched against only has 4 components. How can you fix the Seq pattern to match the Seq value?
- You can test your modifications of eval by loading yourAccounName-SimprexEnvInterp.sml into the *sml* buffer and evaluating the expression SimprexEnvInterp.testEval();. This will display the results of various test cases for eval.

3. Metaprogramming Derivations (32 points)

This problem involves the notion of proof-like derivations that show how programming languages are implemented in terms of interpreters and compilers.

Although we did not discuss these derivations in class, they are covered in slides 14 to 19 of the supplementary slides on Metaprogramming posted in the course schedule for Lec 31.

3a. Deriving Implementations (16 points)

As presented in slides 14 to 19 of the Metaprogramming slides there are two basic reasoning rules involving interpreters, translators (a.k.a. compilers), and program implementation:

The Interpreter Rule (I)

$\frac{P\text{-in-}L\text{ program} \qquad L\text{ interpreter machine}}{P\text{ machine}} (I)$

The Translator Rule (T)

$\frac{P\text{-in-}S\text{ program} \qquad S\text{-to-}T\text{ translator machine}}{P\text{-in-}T\text{ program}} (T)$

In practice, we often elide the word “machine” for interpreter machines and translator machines. For example, we will refer to an “L interpreter machine” as an “L interpreter”, and an “S-to-T translator machine” as an “S-to-T translator” or “S-to-T compiler”. We will also often elide the word “program”; e.g., we will refer to a “P-in-L program” as “P-in-L”. So an “L interpreter” means an “L interpreter machine” while a “S-in-L interpreter” means an “S-in-L interpreter program”. Similar remarks hold for translators (also called compilers): an “S-to-T translator” means an “S-to-T translator machine”, while a “S-to-T-in-L translator” means an “S-to-T-in-L translator program”.

Example

The Metaprogramming slides consider an example with the following elements:

a 251-web-page-in-HTML program (i.e., a 251 web page written in HTML)
an HTML-interpreter-in-C program (i.e., a web browser written in C)
a C-to-x86-compiler-in-x86 program (i.e., a C-to-x86 compiler written in x86)
a x86 computer (i.e., an x86 interpreter machine)

They can be used to build a 251 web page display machine as follows:

$\cfrac{ \text{251-web-page-in-HTML program} \qquad \cfrac{ \cfrac{ \text{HTML-interpreter-in-C program} \qquad \cfrac{ \text{C-to-x86-compiler-in-x86 program} \qquad \text{x86 computer} }{ \text{C-to-x86 compiler machine} } (I) }{ \text{HTML-interpreter-in-x86 program} } (T) \qquad \text{x86 computer} }{ \text{HTML interpreter machine} } (I) }{ \text{251 web page machine} } (I)$

Feel free to abbreviate by dropping the words “program” and “machine”. “… in …” denotes a program, while “… compiler” and “… translator” denote translator machines and “… interpreter” and “… computer” denote interpreter machines.

$\cfrac{ \text{251 web page in HTML} \qquad \cfrac{ \cfrac{ \text{HTML interpreter in C} \qquad \cfrac{ \text{C-to-x86 compiler in x86} \qquad \text{x86 computer} }{ \text{C-to-x86 compiler} } (I) }{ \text{HTML interpreter in x86} } (T) \qquad \text{x86 computer} }{ \text{HTML interpreter} } (I) }{ \text{251 web page machine} } (I)$

Writing Derivations

Rather that displaying derivations using horizontal lines, it is recommended that you use nested bullets to indicate the same structure as the inference rules (though drawn “upside down”). For example, the derivation above could also be written:

251 web page machine (I)

* 251-web-page-in-HTML program

* HTML interpreter machine (I)

  * HTML-interpreter-in-x86 program (T)

    * HTML-interpreter-in-C program

    * C-to-x86 compiler machine (I)

      * C-to-x86-compiler-in-x86 program

      * x86 computer

  * x86 computer

Questions

i. (8 points) Suppose you are given the following:

A P-in-Java program
a Java-to-C-compiler-in-Racket program (i.e., a Java-to-C compiler written in Racket);
a Racket-interpreter-in-x86 program (i.e., a Racket interpreter written in x86 machine code);
a C-to-x86-compiler-in-x86 program (i.e., a C-to-x86 compiler written in x86 code);
an x86 computer (i.e., an x86 interpreter machine).

Using the two reasoning rules above, construct a “proof” that demonstrates how to execute the P-in-Java program on the computer. That is, show how to construct a P machine.

ii. (8 points) Suppose you are given:

a GraphViz-in-C program
a C-to-LLVM-compiler-in-x86 program
an LLVM-to-JavaScript-compiler-in-x86 program
a JavaScript-interpreter-in-ARM program
an x86 computer (i.e., an x86 interpreter machine, such as your laptop)
an ARM computer (i.e., an ARM interpreter machine, such as a smartphone)

Show how to construct a GraphViz machine.

Notes:

In the above two parts, it is not possible to derive a “C interpreter”, a “Java interpreter”, or an “LLVM interpreter”, so if you need or use such a part in your derivation, you’ve done something wrong.
As shown in the above examples, you should use an (I) or (T) to indicate a conclusion that results from the Interpreter or Translator rule, respectively. Double check that the conclusion is actually justified by the rule from two nested bullets below the conclusion.

3b. Bootstrapping (16 points)

In his Turing Award lecture-turned-short-paper Reflections on Trusting Trust, Ken Thompson describes how a compiler can harbor a so-called “Trojan horse” that can make compiled programs insecure. Read this paper carefully and do the following tasks to demonstrate your understanding of the paper:

i. (6 points) Stage II of the paper describes how a C compiler can be “taught” to recognize '\v' as the vertical tab character. Using the same kinds of components and processes used in Problem 1, we can summarize the content of Stage II by carefully listing the components involved and describing (by constructing a proof) how a C compiler that “understands” the code in Figure 2.2 can be generated. (Note that the labels for Figures 2.1 and 2.2 are accidentally swapped in the paper.) In Stage II, two languages are considered:

the usual C programming language
C+\v = an extension to C in which '\v' is treated as the vertical tab character (which has ASCII value 11).

Suppose we are given the following:

a C-to-binary compiler machine (Here, “binary” is the machine code for some machine. This compiler is just a “black box”; we don’t care where it comes from);
a C+\v-to-binary-compiler-in-C program (Figure 2.3 in Thompson’s paper);
a C+\v-to-binary-compiler-in-C+\v program (what should be Figure 2.2 in Thompson’s paper);
a machine that executes the given type of binary code (i.e., a binary interpreter machine)

Construct a proof showing how to use the C+\v-to-binary-compiler-in-C+\v source code to create a C+\v-to-binary-compiler-in-binary program.

ii. (10 points) Stage III of the paper describes how to generate a compiler binary harboring a “Trojan horse”. Using the same kinds of components and processes used in Problem 1, we can summarize the content of Stage III by carefully listing the components involved and describing (by constructing a proof) how the Trojaned compiler can be generated. In particular, assume we have the parts for this stage:

a C-to-binary-compiler machine (again, just a “black box” we are given);
a C-to-binary-compiler-in-C program without Trojan Horses (Figure 3.1 in Thompson’s paper);
a C-to-binary-compiler_TH-in-C program with two Trojan Horses (Figure 3.3 in Thompson’s paper);
a login-in-C program with no Trojan Horse;
a binary-based computer (i.e., a binary interpreter machine)

The subscript _TH indicates that a program contains a Trojan Horse. A C-to-binary compiler_TH has the “feature” that it can insert Trojan Horses when compiling source code that is an untrojaned login program or an untrojaned compiler program. That is, if P is a login or compiler program, it is as if there is a new rule:

The Trojan Horse Rule (TH)

$\cfrac{ P\text{-in-C program} \qquad \text{C-to-binary-compiler}_{TH}\ \text{machine} }{ P_{TH}\text{-in-binary} } (TH)$

Using these parts along with the two usual rules (I) and (T) and the new rule (TH), show how to derive a Trojaned login program login_TH-in-binary that is the result of compiling the uninfected login-in-C program with a C compiler that is itself the result of compiling the uninfected C-to-binary-compiler-in-C program. The interesting thing about this derivation is that login_TH-in-binary is infected with a Trojan horse even though it is compiled using a C compiler whose source code (C-to-binary-compiler-in-C program) contains no code for inserting Trojan horses!

Notes:

Although only 3 pages long, the Thompson paper is very dense and challenging. Don’t be surprised if it requires multiple readings to ``get’’ the ideas, which are profound.
Double-check your derivations to make sure that they make sense and actually describe what’s being said in Thompson’s paper.

Extra Credit Problem 1: Self-printing Program (15 points)

In his Turing-lecture-turned-short-paper Reflections on Trusting Trust, Ken Thompson notes that it is an interesting puzzle to write a program in a language whose effect is to print out a copy of the program. We will call this a self-printing program. Write a self-printing program in any general-purpose programming language you choose. Your program should be self-contained — it should not read anything from the file system.

Important Note: There are lots of answers on the Internet, but you will get zero points if you just copy one of those. (I can tell!) Write this program from scratch completely on your own, without looking anything up online.

Extra Credit Problem 2: Partial Evaluation (25 points)

Avoiding Magic Constants

It is good programming style to avoid “magic constants” in code by explicitly calculating certain constants from others. For instance, consider the following two Bindex programs for converting years to seconds:

; Program 1
(bindex (years)
  (* 31536000 years))

; Program 2
(bindex (years)
  (bind seconds-per-minute 60 
    (bind minutes-per-hour 60
      (bind hours-per-day 24
        (bind days-per-year 365 ; ignore leap years
          (bind seconds-per-year (* seconds-per-minute 
                                    (* minutes-per-hour 
                                       (* hours-per-day days-per-year)))
            (* seconds-per-year years)))))))

The first program uses the magic constant 31536000, which is the number of seconds in a year. (It is worth noting that this number is approximately π × 10⁷. So a century is approximately π × 10⁹ seconds, which means that π seconds is approximately one nano-century!)

The second program shows how this constant is calculated from simpler constants. By showing the process by which seconds-per-year is calculated, the second program is a more robust and well-documented software artifact. Calculated constants also have the advantage that they are easier to modify. Although the numbers in the above program aren’t going to change, there are many so-called “constants” built into a program that change over its lifetime. For instance, the size of word of computer memory, the price of a first-class stamp, and the rate for a certain tax bracket are all numbers that could be hard-wired into programs but which might need to be updated in future version of the software.

However, magic constants can have performance advantages. In the above programs, the program with the magic constant performs one multiplication, while the other program performs four multiplications. If performance is critical, the programmer might avoid the clearer style and instead opt for magic constants.

Partial Evaluation

Is there a way to get the best of both approaches? Yes! We can write our program in the clearer style, and then automatically transform it to the more efficient style via a process known as partial evaluation. Partial evaluation transforms an input program into a residual program that has the same meaning by performing computation steps that would otherwise be performed when running the program. Any computation steps that can be performed during partial evaluation are steps that do not need to be performed when the residual program is run later. In most cases, the residual program has better run-time performance than the original program.

For instance, we can use partial evaluation to systematically derive the first program above from the second. We begin via a step known as constant propagation, in which we substitute the four constants at the top of the second program into their references to yield:

(bindex (years)
  (bind seconds-per-minute 60
    (bind minutes-per-hour 60 
      (bind hours-per-day 24
        (bind days-per-year 365 ; ignore leap years
          (bind seconds-per-year (* 60 (* 60 (* 24 365)))
            (* seconds-per-year years)))))))

Next, we eliminate the now-unnecessary first four bindings via a step known as dead code removal:

(bindex (years)
  (bind seconds-per-year (* 60 (* 60 (* 24 365)))
    (* seconds-per-year years)))

We can now perform the three multiplications involving manifest integers in a step known as constant folding:

(bindex (years)
  (bind seconds-per-year 31536000
    (* seconds-per-year years)))

Finally, another round of constant propagation and dead code removal yields the first program:

(bindex (years)
  (* 31536000 years))

It is not possible to eliminate bindings whose definition ultimately depends on the program parameters. Nevertheless, it is often possible to partially simplify such definitions. For example, consider:

(bindex (a)
  (bind b (* 3 4)
    (bind c (+ a (- 15 b)) 
      (bind d (/ c b)
        (* d c)))))

The transformation techniques described above can simplify this program to:

(bindex (a)
  (bind c (+ a 3)
    (bind d (/ c 12) (* d c))))

In this example, (+ a (- 15 b)) cannot be replaced by a number (because the value of a is unknown), but it can be simplified to the residual expression (+ a 3). Similarly, (/ c b) is transformed to the residual expression (/ c 12) and (bind b ...) is transformed to the residual expression (bind c (+ a 3) (bind d (/ c 12) (* d c))).

Setup

Before beginning this part, you should rename the files BindexPartialEval.sml and BindexPartialEvalTest.sml to be yourAccountName-BindexPartialEval.sml and yourAccountName-BindexPartialEvalTest.sml. In the file yourAccountName-BindexPartialEvalTest.sml, you also need to change the first line of the file from

use "../ps7/BindexPartialEval.sml";

use "../ps7/yourAccountName-BindexPartialEval.sml";

Your Task

In this problem, your task is to flesh out the definition of a function partialEval that performs partial evaluation on a Bindex program. Given a Bindex program, partialEval should return another Bindex program that has the same meaning as the original program, but which also satisfies the following properties:

The program should not contain any bind expressions in which a variable is bound to an integer literal.
The program should not contain any binary applications in which an arithmetic operator is applied to two integer literals. There are two exceptions to this property: the program may contain binary applications of the form (/ n 0) or (% n 0), since performing these applications would cause an error in the partial evaluation process.

It is possible to write separate functions that perform the constant propagation, constant folding, and dead-code elimination steps, but it is tricky to get them to work together to perform all simplifications. It turns out that it is much more straightforward to perform all three kinds of simplification at the same time in a single walk over the expression tree.

By analogy with BindexEnvInterp.eval, partial evaluation of an expression can be performed by the peval function:

val peval: Bindex.exp -> int Env.env -> Bindex.exp:

Given a Bindex expression exp and a partial evaluation environment env, returns the partially evaluated version of exp. The partial evaluation environment contains name/value bindings for names whose integer values are known.

The function that corresponds with BindexEnvInterp.run is partialEval:

(* val partialEval: Bindex.pgm -> Bindex.pgm *)
(* Returns a partially evaluated version of the given Bindex program. *)
fun partialEval (Bindex(fmls,body)) = Bindex(fmls, peval body Env.empty)

Your goal is to implement simplification by fleshing out the peval function definition in BindexPartialEval.sml.

Note that there is a correspondence between run/eval in BindexEnvInterp and partialEval/peval. peval is effectively a version of eval that evaluates as much of an expression as it can based on the “partial” environment information it is given. Because bindings for some names may be missing in the environment, peval cannot always evaluate every expression to the integer it denotes and in some cases must instead return a residual expression that will determine the value when the program is executed. Because of this, peval must always return an expression rather than an integer; even in the case where it can determine the value of an expression, that value must be expressed as an integer literal node (tagged with the Int constructor), not an integer.

Notes:

Use BindexEnvInterp.binopToFun as part of applying an operator to two integers.
Divisions and remainders whose second operands are zero must be left in the program. Such programs will encounter divide-by-zero errors when they are later executed. For example,
```
(bindex (a)
  (bind b (* 3 4)
    (bind c (/ b (- 12 b)) (* c b))))
```
should be transformed to:
```
(bindex (a)
  (bind c (/ 12 0)
    (* c 12)))
```
In some cases it would be possible to perform more aggressive simplification if you took advantage of algebraic properties like the associativity and commutativity of addition and multiplication. To simplify this problem, you should not use any algebraic properties of the arithmetic operators. For example, you should not transform (+ 1 (+ a 2)) into (+ 3 a), but should leave it as is. You should not even perform “obvious” simplifications like (+ 0 a) ⇒ a, (* 1 a) ⇒ a, and (* 0 a) ⇒ 0. Although the first two of these simplification are valid, the last is unsafe in the sense that it can change the meaning of a program. For instance, (* 0 (/ a b)) cannot be simplified to 0, because it does not preserve the meaning of the program in the case where b is 0 (in which case evaluating the expression should give an error).
In order to test your partial evaluator, load yourAccountName-BindexPartialEvalTest.sml into an *sml* buffer, and evaluate BindexPartialEvalTest.testAll(). This applies your partial evaluator to all the test entries in the list testEntries in the file yourAccountName-BindexPartialEvalTest.sml. The entries in this list are by no means exhaustive. You are strongly encouraged to add more entries to this list. If all tests succeed, you will see this:
```
- BindexPartialEvalTest.testAll();
Add-2-3 -- OK!
Simple1 -- OK!
Years -- OK!
Residuals1 -- OK!
Residuals2 -- OK!
Residuals3 -- OK!
```
If any tests fail, testAll() will show the actual output vs expected output.

To test your partial evaluator on individual programs, you can use the BindexPartialEvalTest.testPartialEval function, which takes a string representation of a Bindex program. For example:

- BindexPartialEvalTest.testPartialEval "(bindex () (+ 1 2))";
(bindex () 3)
val it = () : unit

- BindexPartialEvalTest.testPartialEval "(bindex (a)\
=                 \  (bind b (* 3 4)\
=                 \    (bind c (/ b (- 12 b)) (* c b))))";
(bindex (a) (bind c (/ 12 0) (* c 12)))
val it = () : unit

- BindexPartialEvalTest.testPartialEval "(bindex (a)\
=                 \  (+ (* (+ 1 2) a)\
=                 \     (+ (* 3 4)\
=                 \        (+ (* 0 a)\
=                 \           (+ (* 1 a)\
=                 \              (+ 0 a))))))";
(bindex (a) (+ (* 3 a) (+ 12 (+ (* 0 a) (+ (* 1 a) (+ 0 a))))))
val it = () : unit

The last two examples show the SML conventions for entering multiline strings. Each nonterminal line must end with a backslash character, and the next line must begin with a backslash character.