PS2: Racket List Recursion
-
Changes/clarifications shown in magenta.
- Dueish: Deadline extended until Mon Nov 09
- Notes:
-
This pset has lots Racket programming. Start soon.
-
As with all regular psets, you can work on this problem in a two-person team or as an individual. You need to work with a different partner than you did in PS1. Use this Pset Partner Doc to find a partner and record your partnership.
- Here’s the background you need for the various problems:
- Problem 1 is based on the discussion of recursive functions in the slides for Lec 06 on Racket Function Semantics
- Problem 2 is based on the discussion of pairs and lists in Lec 07.
- Problems 3 and 4 are based on the coverage of list recursion in Lec 08/09
- Problem 4b should use the
letconstruct, which is introduced in Lec 10.
-
The problems needn’t be done in order. Feel free to jump around.
- Do not use DrRacket’s “box comments” in your code. They interact poorly with our grading infrastructure. Instead, if you wish to comment out a block with multiple lines of code, use
#|to begin the block comment and|#to end the block comment. Thankfully, block comments in Racket nest properly, unlike the completely and unacceptably broken block comment ``feature” in Java/C/JavaScript.
-
-
Recorded Times from some previous semesters (in hours)
Times Problem 1 Problem 2 Problem 3 Problem 4 Total average time 2.11 0.79 1.29 3.62 7.81 median time 1 0.66 1.0 3.00 5.66 25% took more than 2.5 1.0 1.5 4.75 9.75 10% took more than 3 1.05 2.08 7.00 13.13 -
How to Start PS2
- Follow the instructions in the GDoc CS251-F20-T2 Pset Submission Instructions for creating your PS2 Google Doc. Put all written answers and a copy of all code into this PS2 GDoc. If you are working with a partner, only one of you needs to create this document, but you should link it from both of your List Docs.
- Submission:
- For all parts of all problems, include all answers (including Racket code and small-step derivations) in your PS2 GDoc. Please format your small-step derivation in Problem 1 and your Racket function definitions in Problems 3 and 4 and so that they’re easy to read. Format all derivations and code using a fixed-width font (Courier New or Consolas). You use a small font size if that helps.
- For Problem 1 (Sum Fun), include your derivations and answers to all questions in your PS2 doc.
- For Problem 2 (Box-and-pointer diagrams), include all expressions in your PS2 doc.
- For Problems 3 and 4 (Recursive Racket List Functions):
- Be sure that all function definitions in
yourAccountName-ps2-list-functions.rktalso appear in your PS2 Doc (so that I can comment on them) - When you are finished with Problems 3 and 4, drop a copy of your
yourAccountName-ps2-list-functions.rktin your~/cs251/drop/ps02drop folder on cs.wellesley.edu. If you are working with a partner, only one of you should do this. At the top of your PS2 doc and in the PS2 entry in your List Doc, indicate the account name of the drop folder in which the.rktfile has been dropped.
- Be sure that all function definitions in
1. Sum Fun (25 points)
In the Lec 06 slides, the following recursive factorial function is covered:
(define fact
(lambda (n)
(if (= n 0)
1
(* n (fact (- n 1))))))The the small-step semantics introduced in Lec 06 can be used to explain the evaluation of (fact 4). To simplify things, let’s introduce the abbreviation λ_fact for the follow lambda expression:
(lambda (n) (if (= n 0) 1 (* n (fact (- n 1)))))Then here is the small-step evaluation derivation for (fact 4) relative to an implicit environment that binds the name fact to the expression λ_fact:
({fact} 4)
⇒ {(λ_fact 4)} [varref]
⇒ (if {(= 4 0)} 1 (* 4 (fact (- 4 1)))) [function call]]
⇒ {(if #f 1 (* 4 (fact (- 4 1))))} [equality]
⇒ (* 4 ({fact} (- 4 1))) [if false]
⇒ (* 4 (λ_fact {(- 4 1)})) [varref]
⇒ (* 4 {(λ_fact 3)}) [subtraction]
⇒ (* 4 (if {(= 3 0)} 1 (* 3 (fact (- 3 1))))) [function call]
⇒ (* 4 {(if #f 1 (* 3 (fact (- 3 1))))}) [equality]
⇒ (* 4 (* 3 ({fact} (- 3 1)))) [if false]
⇒ (* 4 (* 3 (λ_fact {(- 3 1)}))) [varref]
⇒ (* 4 (* 3 {(λ_fact 2)})) [subtraction]
⇒ (* 4 (* 3 (if {(= 2 0)} 1 (* 2 (fact (- 2 1)))))) [function call]
⇒ (* 4 (* 3 {(if #f 1 (* 2 (fact (- 2 1))))})) [equality]
⇒ (* 4 (* 3 (* 2 ({fact} (- 2 1))))) [if false]
⇒ (* 4 (* 3 (* 2 (λ_fact {(- 2 1)})))) [varref]
⇒ (* 4 (* 3 (* 2 {(λ_fact 1)}))) [subtraction]
⇒ (* 4 (* 3 (* 2 (if {(= 1 0)} 1 (* 1 (fact (- 1 1))))))) [function call]
⇒ (* 4 (* 3 (* 2 {(if #f 1 (* 1 (fact (- 1 1))))}))) [equality]
⇒ (* 4 (* 3 (* 2 (* 1 ({fact} (- 1 1)))))) [if false]
⇒ (* 4 (* 3 (* 2 (* 1 (λ_fact {(- 1 1)}))))) [varref]
⇒ (* 4 (* 3 (* 2 (* 1 {(λ_fact 0)})))) [subtraction]
⇒ (* 4 (* 3 (* 2 (* 1 (if {(= 0 0)} 1 (* 0 (fact (- 0 1)))))))) [function call]
⇒ (* 4 (* 3 (* 2 (* 1 {(if #t 1 (* 0 (fact (- 0 1))))})))) [equality]
⇒ (* 4 (* 3 (* 2 {(* 1 1)}))) [if nonfalse]
⇒ (* 4 (* 3 {(* 2 1)})) [multiplication]
⇒ (* 4 {(* 3 2)}) [multiplication]
⇒ {(* 4 6)} [multiplication]
⇒ 24 [multiplication]To highlight the essential steps of such an evaluation, we will often use the notation E1 ⇒* E2 to mean that expression E1 rewrites to expression E2 by some number (possibly zero) of ⇒ steps. Below, we use this notation to omit all lines except for the ones involving (1) calls to λ_fact on argument values or (2) calculation of the final result. Below is an example of an abbreviated evaluation derivation for the above example. Note that lines involving ⇒* do not have an explicit justification in square brackets (though the could be justified by all of the rules applied in ⇒*).
({fact} 4)
⇒ {(λ_fact 4)} [varref]
⇒* (* 4 {(λ_fact 3)})
⇒* (* 4 (* 3 {(λ_fact 2)}))
⇒* (* 4 (* 3 (* 2 {(λ_fact 1)})))
⇒* (* 4 (* 3 (* 2 (* 1 {(λ_fact 0)}))))
⇒* (* 4 (* 3 (* 2 {(* 1 1)})))
⇒ (* 4 (* 3 {(* 2 1)})) [multiplication]
⇒ (* 4 {(* 3 2)}) [multiplication]
⇒ {(* 4 6)} [multiplication]
⇒ 24 [multiplication]As another example, consider a recursive definition of a function for calculating the nth Fibonacci number, also shown in the Lec 06 slides:
(define fib
(lambda (n)
(if (<= n 1)
n
(+ (fib (- n 1)) (fib (- n 2))))))Suppose λ_fib is an abbreviation for the following lambda expression:
(lambda (n)
(if (<= n 1)
n
(+ (fib (- n 1)) (fib (- n 2))))))Then here is an abbreviated evaluation derivation for (fib 4) relative to an implicit environment that binds the name fib to the expression λ_fib:
({fib} 4)
⇒ {(λ_fib 4)} [varref]
⇒* (+ {(λ_fib 3)} (fib (- 4 2)))
⇒* (+ (+ {(λ_fib 2)} (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ (+ {(λ_fib 1)} (fib (- 2 2))) (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ (+ 1 {(λ_fib 0)}) (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ {(+ 1 0)} (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ 1 {(λ_fib 1)}) (fib (- 4 2)))
⇒* (+ {(+ 1 1)} (fib (- 4 2)))
⇒* (+ 2 {(λ_fib 2)})
⇒* (+ 2 (+ {(λ_fib 1)} (fib (- 2 2))))
⇒* (+ 2 (+ 1 {(λ_fib 0)}))
⇒* (+ 2 {(+ 1 0)})
⇒ {(+ 2 1)} [addition]
⇒ 3 [addition]Note that (λ_fib 4) ⇒* (+ (λ_fib 3) (fib (- 4 2))) and not (λ_fib 4) ⇒* (+ (λ_fib 3) (λ_fib 2)). Why? Because the small-step evaluation of (+ E1 E2) must fully evaluate E1 to a value V1 before any evaluation is performed on E2. So the expression (fib (- 4 2)) is not simplified in any way until (λ_fib 3) evaluates to 2.
Also note that ⇒* (+ (+ 1 0) (fib (- 3 2))) ⇒ (+ 1 (fib (- 3 2))) and not (+ (+ 1 0) (fib (- 3 2))) ⇒ (+ (+ 1 0) (λ_fib 1)). The addition redex (+ 1 0) must be evaluated to 1 before any work is done reducing (fib (- 3 2)).
In this problem you are asked to reason about and create such abbreviated small-step derivations involving recursive function definitions.
a. sum-between (5 points)
Here is a definition of a sum-between function that returns the sum of all the integers between its two integer arguments (inclusive):
(define sum-between
(lambda (lo hi)
(if (> lo hi)
0
(+ lo (sum-between (+ lo 1) hi)))))Using the abbreviated small-step derivation notation shown above for (fact 4), show an abbreviated evaluation derivation for (sum-between 3 7) that shows the key steps in this derivation. Use the notation λ_sb as an abbreviation for the lambda expression
(lambda (lo hi)
(if (> lo hi)
0
(+ lo (sum-between (+ lo 1) hi))))Your derivation should only show lines in which λ_sb is called on values and lines involving the calculation of + in (+ lo ...), but not any lines that involve if, >, or the calculation of + in (+ lo 1).
b. Stack depth for sum-between (3 points)
Although the small-step evaluation model does not have any explicit notion of stack frames, operations like * in the recursive fact definition and + in the recursive sum-between definition correspond to pending operations that are remembered to be performed when control returns from the stack frame for a particular function invocation in a model based on stack frames. In the (fact 4) example, the fact that the maximal sequence of nested multiplications, (* 4 (* 3 (* 2 (* 1 1)))), has four multiplications corresponds to a nesting of five stack frames (one for each call of fact on arguments 4 down to 0).
In the case of fact, we will call the maximal number of pending multiplications the stack depth. So (fact 4) has a stack depth of 4, and (fact 100) would have a stack depth of 100. So the stack depth of (fact n) grows linearly in n.
Let’s define the stack depth for sum-between to be the maximal number of nested pending addition operations in the small-step evaluation derivation.
-
What is the stack depth for
(sum-between 3 7)? -
What is the stack depth for
(sum-between 1 128)? -
How does the stack depth for
(sum-between 1 n)grow withn?
c. sum-between-halves (8 points)
Here is a definition of a sum-between-halves function that also returns the sum of all the integers between its two integer arguments (inclusive), but does so in a different way from sum-between:
(define sum-between-halves
(lambda (lo hi)
(if (> lo hi)
0
(if (= lo hi)
lo
(+ (sum-between-halves lo (quotient (+ lo hi) 2))
(sum-between-halves (+ 1 (quotient (+ lo hi) 2)) hi))))))Show an abbreviated evaluation derivation for (sum-between-halves 3 7) that shows the key steps in this derivation. Use the notation λ_sbh as an abbreviation for the lambda expression
(lambda (lo hi)
(if (> lo hi)
0
(if (= lo hi)
lo
(+ (sum-between-halves lo (quotient (+ lo hi) 2))
(sum-between-halves (+ 1 (quotient (+ lo hi) 2)) hi))))))Your derivation should be similar to the (fib 4) example given above. Note that somes lines will have a mixture of calls to λ_sbh on values and calls to sum-between-halves on unevaluated expressions. See the (fib 4) example for an explanation of this. For example, your derivation should begin like this:
(λ_sbh 3 7)
⇒* (+ (λ_sbh 3 5)
(sum-between-halves (+ 1 (quotient (+ 3 7) 2)) 7))
⇒* (+ (+ (λ_sbh 3 4)
(sum-between-halves (+ 1 (quotient (+ 3 5) 2)) 5))
(sum-between-halves (+ 1 (quotient (+ 3 7) 2)) 7))d. Stack depth for sum-between-halves (4 points)
Define the stack depth for a call to sum-between-halves as the maximal number of nested pending + operations from (+ (sum-between-halves ...) (sum-between-halves ...)).
-
What is the stack depth for
(sum-between-halves 3 7)? -
What is the stack depth for
(sum-between-halves 1 128)? -
How does the stack depth for
(sum-between-halves 1 n)grow withn? -
Does
sum-between-halvesoffer any benefit oversum-betweenas a way to calculate the sum of integers in a range?
e. sum-between-iter (3 points)
Now we consider one more way to calculate the sum of integers in a given range. The function sum-between-iter defined below also sums numbers in a given range using the helper function sum-between-tail.
(define sum-between-iter
(lambda (lo hi)
(sum-between-tail lo hi 0)))
(define sum-between-tail
(lambda (lo hi sum-so-far)
(if (> lo hi)
sum-so-far
(sum-between-tail (+ lo 1) hi (+ lo sum-so-far)))))Show an abbreviated evaluation derivation for (sum-between-iter 3 7) that shows the key steps in this derivation. Use the notation λ_sbi as an abbreviation for the lambda expression
(lambda (lo hi)
(sum-between-tail lo hi 0)))and the notation λ_sbt as an abbreviation for the lambda expression
(lambda (lo hi sum-so-far)
(if (> lo hi)
sum-so-far
(sum-between-tail (+ lo 1) hi (+ lo sum-so-far)))))In your derivation, show only lines in which λ_sbi or λ_sbt are called on values.
f. Benefits of sum-between-iter/sum-between-tail (2 points)
Do sum-between-iter/sum-between-tail offer any benefit(s) over sum-between and sum-between-halves? Explain.
Note: sum-between-tail is an example of a so-called tail-recursive function, which we will study in a few weeks. Racket has no loop constructs, but they are not necessary because it is is possible to write all iterations (loops) in Racket using tail recursion.
2. Box-and-pointer diagrams (15 points)
Consider the following box-and-pointer diagram for the list structure named a:
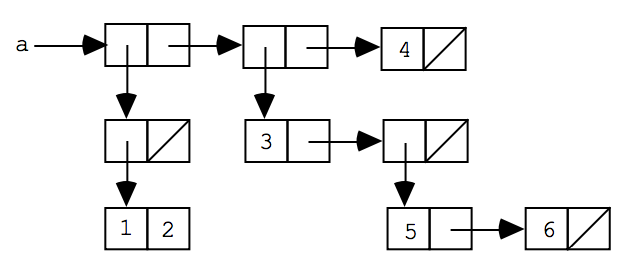
-
(9 points) For each of the numbers 1 through 6, write a Racket expression that uses
carandcdrto extract that number froma. -
(2 points) Write down the printed representation for a (i.e., what would be returned by the Racket interpreter for evaluating
a?). -
(4 points) Write a Racket definition of the form
(define aexpr), where expr is an expression usingcons,list, and the numbers 1 through 6 (but noquoteor quotation) to create the structure depicted in the diagram. To make your expression easy to read, you must used thelistsyntactic sugar whereever it makes sense to do so, and only useconswherelistcannot be used.Once you have defined
ain this way, you may test your expressions from parts a and b.
3. Recursive Racket List Functions, Part 1 (20 points)
In PS1, you wrote some recursive Racket functions that manipulate numbers. Here, you will continue to practice defining recursive Racket functions, but now you focus on functions that manipulate Racket lists. Unlike list and array data structures in many other languages, which are most naturally processed with loops, the linked-list recursively-defined nature of Racket lists make them natural candidates for recursive processing.
For each of the following Racket function specifications, write and test a recursive function that satisfies that specification. In all of your definitions, you should use the following recursive problem solving strategy:
-
For which argument(s) (known as the base case(s)) is the function so simple that the answer can be returned immediately?
-
For the other case(s) (known as the general case(s) or recursive case(s)), use divide/conquer/glue:
-
divide: make one or more subproblems that are smaller instances of the given problem;
-
conquer: assume that the recursive function you’re defining simply works and returns the correct answer on all of the smaller problems.
-
glue: combine the result(s) of the recursive function call(s) with information in the original problem to create the correct result for the whole problem.
-
Notes:
-
For Problems 3 and 4, you should use Dr. Racket to create a single file named
yourAccountName-ps2-list-functions.rktthat contains all the functions (including helper functions) that you define for this problem. -
In your definitions, unless otherwise instructed, you should not introduce any recursive helper functions. (But you can define nonrecursive helper functions).
-
In your definitions, you are not allowed to use higher-order list functions like
map,filter, orfoldr. You will be able to use these higher-order functions in similar problems later on PS3, but not now in PS2. -
If the following error message pops up during the testing of one of your functions, it mostly likely means that you have an infinite recursion that doesn’t reach its base case and runs out of memory due to a stack depth that cannot fit into available memory.
-
(4 points) Define a function
map-remainderthat takes two arguments (an integerdivisorand a listintsof integers) and returns an integer list the same length asintsin which every element is remainder of dividing the corresponding element ofintsbydivisor.> (map-remainder 2 (list 16 23 42 57 64 100)) '(0 1 0 1 0 0) > (map-remainder 3 (list 16 23 42 57 64 100)) '(1 2 0 0 1 1) > (map-remainder 5 (list 16 23 42 57 64 100)) '(1 3 2 2 4 0) > (map-remainder 17 (list 16 23 42 57 64 100)) '(16 6 8 6 13 15) -
(4 points) Define a function
filter-divisible-bythat takes two arguments (an integerdivisorand a listintsof integers) and returns a new integer list containing all the elements ofintsthat are divisible bydivisor. Usedivisible-by?from above to determine divisibility.> (filter-divisible-by 2 (list 16 23 42 57 64 100)) '(16 42 64 100) > (filter-divisible-by 3 (list 16 23 42 57 64 100)) '(42 57) > (filter-divisible-by 4 (list 16 23 42 57 64 100)) '(16 64 100) > (filter-divisible-by 5 (list 16 23 42 57 64 100)) '(100) > (filter-divisible-by 17 (list 16 23 42 57 64 100)) '()Use the following helper function, which is helpful in this problem and some of the following ones.
(define divisible-by? (lambda (num divisor) (= (remainder num divisor) 0))) -
(4 points) Define a function
contains-multiple?that takes an integermand a list of integersnsthat returns#tifmevenly divides at least one element of the integer listns; otherwise it returns#f. Usedivisible-by?from above to determine divisibility.> (contains-multiple? 5 (list 8 10 14)) #t > (contains-multiple? 3 (list 8 10 14)) #f > (contains-multiple? 5 null) #f -
(4 points) Write a function
all-contain-multiple?that takes an integernand a list of lists of integersnss(pronounced “enziz”) and returns#tif each list of integers innsscontains at least one integer that is a multiple ofn; otherwise it returns#f. Usecontains-multiple?in your definition ofall-contain-multiple?.> (all-contain-multiple? 5 (list (list 17 10 2) (list 25) (list 3 8 5))) #t > (all-contain-multiple? 2 (list (list 17 10 2) (list 25) (list 3 8 5))) #f > (all-contain-multiple? 3 null) #t ; said to be "vacuously true"; there is no counterexample! -
(4 points) Define a function
map-consthat takes any valuexand an n-element listysand returns an n-element list of all pairs'(x . y)whereyranges over the elements ofys. The pair'(x . y)should have the same relative position in the resulting list asyhas inys.> (map-cons 17 (list 8 5 42 23)) '((17 . 8) (17 . 5) (17 . 42) (17 . 23)) > (map-cons 3 (list (list 1 6 2) (list 4 5) (list) (list 9 6 8 7))) '((3 1 6 2) (3 4 5) (3) (3 9 6 8 7)) > (map-cons 42 null) '()
4. Recursive Racket List Functions, Part 2 (40 points)
These are more challenging definitions of recursive functions than in Part 1. For this reason, for each of these functions you are required to explicilty show the following steps of the divide/conquer/glue (DCG) problem solving strategy:
-
For the example input list
Lspecified in each problem:i. Show the result of calling the function on
L;ii. Show the result of calling the function on
(rest L);iii. Write an expression that combines the value of
(first L)with the result in (ii) to yield the result in (i).iv. Generalize the expression in (iii) into an expression for the general case of the recursive function definition.
-
Explain what the recursive function should return when called on the empty list. If you’re not sure, consider the case of calling the function on a singleton list, and reason from the combiner in the general case what the result for the empty list should be. Give a general expression for the base case.
-
Combine the results of parts 1 and 2 to form your final recursive function definition.
Example:
Define a function snoc that takes an element x and a length n list of elements ys and returns a length n+1 list in which x occurs after all the elements in ys.
> (snoc 17 (list 7 2 5))
'(7 2 5 17)-
Suppose
Lis'(7 2 5)in the function call(snoc 17 '(7 2 5))i.
(snoc 17 '(7 2 5))should return'(7 2 5 17).ii.
(rest L)is'(2 5), and(snoc 17 '(2 5))should return'(2 5 17).iii.
(first L)is7. The way to combine 7 and'(2 5 17)to yield'(7 2 5 17)is(cons 17 '(2 5 17)).iv. For
(snoc x ys), the generalization of (iii) is the general case(cons (first ys) (snoc x (rest ys))). -
(snoc 17 '())should return'(17). In general(snoc x '())should return(list x)(which is syntactic sugar for(cons x '()). -
The definition of
snocis:(define (snoc x ys) (if (null? ys) (list x) (cons (first ys) (snoc x (rest ys)))))
Note
In your definitions, you are not allowed to use higher-order list functions like map, filter, or foldr. You will be able to use these higher-order functions in similar problems later on PS3, but not here in PS2.
Your Problems
-
(8 points) Define a function
my-cartesian-productthat takes two listsxsandysand returns a list of all pairs'(x . y)wherexranges over the elements ofxsandyranges over the elements ofys. The pairs should be sorted first by thexentry (relative to the order inxs) and then by theyentry (relative to the order inys).> (my-cartesian-product (list 1 2) (list "a" "b" "c")) ; yes, Racket has string values '((1 . "a") (1 . "b") (1 . "c") (2 . "a") (2 . "b") (2 . "c")) > (my-cartesian-product (list 2 1) (list "a" "b" "c")) '((2 . "a") (2 . "b") (2 . "c") (1 . "a") (1 . "b") (1 . "c")) > (my-cartesian-product (list "c" "b" "a") (list 2 1)) '(("c" . 2) ("c" . 1) ("b" . 2) ("b" . 1) ("a" . 2) ("a" . 1)) > (my-cartesian-product (list "a" "b") (list 2 1)) '(("a" . 2) ("a" . 1) ("b" . 2) ("b" . 1)) > (my-cartesian-product (list 1) (list "a")) '((1 . "a")) > (my-cartesian-product null (list "a" "b" "c")) '()Notes:
- We ask you to name your function
my-cartesian-productbecause Racket already provides a similar (but slightly different)cartesian-productfunction (which you cannot use, of course). - Use the
map-consfunction from above as a helper function in yourcartesian-productdefinition. - Racket’s
appendfunction is helpful here. - For your example list
L, use("a" "b" "c")in the call(my-cartesian-product '("a" "b" "c") '(3 4)).
- We ask you to name your function
-
(9 points) Assume that the elements of a list are indexed starting with 0. Define a function
altsthat takes a listxsand returns a two-element list of lists, the first of which has all the even-indexed elements (in the same relative order as inxs) and the second of which has all the odd-indexed elements (in the same relative order as inxs).> (alts (list 7 5 4 6 9 2 8 3)) '((7 4 9 8) (5 6 2 3)) > (alts (list 5 4 6 9 2 8 3)) '((5 6 2 3) (4 9 8)) > (alts (list 4 6 9 2 8 3)) '((4 9 8) (6 2 3)) > (alts (list 3)) '((3) ()) > (alts null) '(() ())Notes:
-
As in all other problems, You should use the divide/conquer/glue strategy here. In particular, the solution for
(alts elts)should be expressed in terms of combining(first elts)with(alts (rest elts)). -
You should not treat even-length and odd-length cases differently, nor should you handle the singleton list specially.
-
You should use Racket’s
letconstruct (see Lec 09) for declaring local names is helpful to avoiding unnecessarily recalculating the recursive call. -
For your example list
L, use(1 2 3 4 5 6)in the call(alts '(1 2 3 4 5 6))
-
-
(10 points) Define a function
insertsthat takes a valuexand an n-element listysand returns an n+1-element list of lists showing all ways to insert a single copy ofxintoys.> (inserts 3 (list 5 7 1)) '((3 5 7 1) (5 3 7 1) (5 7 3 1) (5 7 1 3)) > (inserts 3 (list 7 1)) '((3 7 1) (7 3 1) ( 7 1 3)) > (inserts 3 (list 1)) '((3 1) (1 3)) > (inserts 3 null) '((3)) > (inserts 3 (list 5 3 1)) '((3 5 3 1) (5 3 3 1) (5 3 3 1) (5 3 1 3))Notes:
- The
map-consfunction from above is useful here. - Think very carefully about the base case and the combination function for the recursive case.
- For your example list
L, use(2 3 4)in the call(inserts 1 '(2 3 4))
- The
-
(13 points) Define a function
my-permutationsthat takes as its single argument a listxsof distinct elements (i.e., no duplicates) and returns a list of all the permutations of the elements ofxs. The order of the permutations does not matter.> (my-permutations null) '(()) > (my-permutations (list 4)) '((4)) > (my-permutations (list 3 4)) '((3 4) (4 3)) ; order doesn't matter > (my-permutations (list 2 3 4)) '((2 3 4) (3 2 4) (3 4 2) (2 4 3) (4 2 3) (4 3 2)) ; order doesn't matter > (my-permutations (list 1 2 3 4)) '((1 2 3 4) (2 1 3 4) (2 3 1 4) (2 3 4 1) (1 3 2 4) (3 1 2 4) (3 2 1 4) (3 2 4 1) (1 3 4 2) (3 1 4 2) (3 4 1 2) (3 4 2 1) (1 2 4 3) (2 1 4 3) (2 4 1 3) (2 4 3 1) (1 4 2 3) (4 1 2 3) (4 2 1 3) (4 2 3 1) (1 4 3 2) (4 1 3 2) (4 3 1 2) (4 3 2 1)) ; order doesn't matterNotes:
- We ask you to name your function
my-permutationsbecause Racket already provides the same function namedpermutations(which you cannot use, of course). - Although the specification allows the permuted elements to be listed in any order, the above examples show an order that works particularly well with the divide/conquer/glue strategy. In particular, study the above examples carefully to understand (1) the recursive nature of
my-permutationsand (2) why theinsertsfunction from above is helpful to use when definingmy-permutations. - In the example
(my-permutations (list 1 2 3 4)), the 24 results would normally be printed by Racket in 24 separate lines, but here they have been formatted to strongly sugggest a particular solution strategy. - For your example list
L, use(1 2 3)in the call(my-permutations '(1 2 3)). - In this problem, you are allowed to use one or more recursive helper functions in your glue step, but are not allowed to use higher-order list functions like
map,append-map, orfoldr. You are not required to show the details of the DCG strategy for the helper functions.
- We ask you to name your function
Extra Credit: Permutations in the Presence of Duplicates (12 points)
This problem is optional. You should only attempt it after completing all the other problems.
Define a divide/conquer/glue recursive version of the my-permutations function named my-permutations-dup that correctly handles lists with duplicate elements. That is, each permutation of such a list should only be listed once in the result As before, the order of the permutations does not matter.
Your function should not generate duplicate permutations and then remove them. Rather, you should just not generate any duplicates to begin with. Also, for full credit, your function should be written in a divide/conquer/glue style of recursion, rather than some sort of iterative algorithm. It is possible to solve this problem with a minor change to the my-permutations/inserts approach from Problem 5d.
Below are some examples. You are not required to list permutations in the same order as in the examples.
> (my-permutations-dup '(1 2 2))
'((1 2 2) (2 1 2) (2 2 1))
> (my-permutations-dup '(2 1 2))
'((2 1 2) (1 2 2) (2 2 1))
> (my-permutations-dup '(2 2 1))
'((2 2 1) (2 1 2) (1 2 2))
> (my-permutations-dup '(1 2 2 2))
'((1 2 2 2) (2 1 2 2) (2 2 1 2) (2 2 2 1))
> (my-permutations-dup '(2 1 2 2))
'((2 1 2 2) (1 2 2 2) (2 2 1 2) (2 2 2 1))
> (my-permutations-dup '(2 2 1 2))
'((2 2 1 2) (2 1 2 2) (1 2 2 2) (2 2 2 1))
> (my-permutations-dup '(2 2 2 1))
'((2 2 2 1) (2 2 1 2) (2 1 2 2) (1 2 2 2))
> (my-permutations-dup '(1 1 2 2))
'((1 1 2 2) (1 2 1 2) (2 1 1 2) (1 2 2 1) (2 1 2 1) (2 2 1 1))
> (my-permutations-dup '(1 2 1 2))
'((1 2 1 2) (2 1 1 2) (1 1 2 2) (1 2 2 1) (2 1 2 1) (2 2 1 1))
> (my-permutations-dup '(1 2 2 1))
'((1 2 2 1) (2 1 2 1) (2 2 1 1) (1 2 1 2) (2 1 1 2) (1 1 2 2))
> (my-permutations-dup '(1 1 2 2 2))
'((1 1 2 2 2) (1 2 1 2 2) (2 1 1 2 2) (1 2 2 1 2) (2 1 2 1 2)
(2 2 1 1 2) (1 2 2 2 1) (2 1 2 2 1) (2 2 1 2 1) (2 2 2 1 1))
> (my-permutations-dup '(1 2 1 2 2))
'((1 2 1 2 2) (2 1 1 2 2) (1 1 2 2 2) (1 2 2 1 2) (2 1 2 1 2)
(2 2 1 1 2) (1 2 2 2 1) (2 1 2 2 1) (2 2 1 2 1) (2 2 2 1 1))
> (my-permutations-dup '(1 2 2 1 2))
'((1 2 2 1 2) (2 1 2 1 2) (2 2 1 1 2) (1 2 1 2 2) (2 1 1 2 2)
(1 1 2 2 2) (1 2 2 2 1) (2 1 2 2 1) (2 2 1 2 1) (2 2 2 1 1))
> (my-permutations-dup '(1 2 2 2 1))
'((1 2 2 2 1) (2 1 2 2 1) (2 2 1 2 1) (2 2 2 1 1) (1 2 2 1 2)
(2 1 2 1 2) (2 2 1 1 2) (1 2 1 2 2) (2 1 1 2 2) (1 1 2 2 2))
> (my-permutations-dup '(2 1 1 2 2))
'((2 1 1 2 2) (1 2 1 2 2) (1 1 2 2 2) (2 1 2 1 2) (1 2 2 1 2)
(2 2 1 1 2) (2 1 2 2 1) (1 2 2 2 1) (2 2 1 2 1) (2 2 2 1 1))
> (my-permutations-dup '(2 1 2 1 2))
'((2 1 2 1 2) (1 2 2 1 2) (2 2 1 1 2) (2 1 1 2 2) (1 2 1 2 2)
(1 1 2 2 2) (2 1 2 2 1) (1 2 2 2 1) (2 2 1 2 1) (2 2 2 1 1))
> (my-permutations-dup '(2 1 2 2 1))
'((2 1 2 2 1) (1 2 2 2 1) (2 2 1 2 1) (2 2 2 1 1) (2 1 2 1 2)
(1 2 2 1 2) (2 2 1 1 2) (2 1 1 2 2) (1 2 1 2 2) (1 1 2 2 2))
> (my-permutations-dup '(2 2 1 1 2))
'((2 2 1 1 2) (2 1 2 1 2) (1 2 2 1 2) (2 1 1 2 2) (1 2 1 2 2)
(1 1 2 2 2) (2 2 1 2 1) (2 1 2 2 1) (1 2 2 2 1) (2 2 2 1 1))
> (my-permutations-dup '(2 2 1 2 1))
'((2 2 1 2 1) (2 1 2 2 1) (1 2 2 2 1) (2 2 2 1 1) (2 2 1 1 2)
(2 1 2 1 2) (1 2 2 1 2) (2 1 1 2 2) (1 2 1 2 2) (1 1 2 2 2))
> (my-permutations-dup '(2 2 2 1 1))
'((2 2 2 1 1) (2 2 1 2 1) (2 1 2 2 1) (1 2 2 2 1) (2 2 1 1 2)
(2 1 2 1 2) (1 2 2 1 2) (2 1 1 2 2) (1 2 1 2 2) (1 1 2 2 2))