PS6: I Never Metalanguage I Didn't Like

• Changes from the original PS6 description are highlighed in magenta.

• This is the final version of PS6, which includes Problem 5 on interpreting and compiling the Condex language.

• This is the last required regular pset. There will be a PS7, but it will be completely optional.

• Dueish: Fri Dec 11.

• Notes:
  • This pset has 120 total points.
  • You can do Problems 1 and 2 based on material through the Thu. Dec. 03 Lec 27 material on symbols and s-expressions.
  • You can do Problem 3 based on the Racket PostFix material started in the Fri. Dec. 04 Lec 28 and finished in the Mon. Dec. 07 Lec 29.
  • You can do Problem 5a based on the coverage of the Intex Interpreter in ~/cs251/sml/intex/Intex.sml in Lec 31 on Wed Dec 09.
  • Problems 4, 5b, and 5c, depend on coverage of the depth-based Intex-to-PostFix compiler that won’t be finished until the beginning of Lec 32 on Thu Dec 10, so you might want to wait until after that class to start these problems. If you’d like to start these problems before then, look at the discussion of the Intex-to-PostFix compiler at the end of the Intex slides and/or the implementation of the Intex-to-PostFix compiler in ~/cs251/sml/intex/IntexToPostFix.sml.
    • You should complete Problem 4 before starting Parts 5b and 5c on compiling Condex to PostFix.

• Times (in hours) from some previous semesters:

  The following times do not include Problems 2 and 5, which are new problems.

  Times	Problem 1	Problem 3	Problem 4	Total (w/o Probs 2 and 5!)
  average time (hours)	0.5	2.5	1.9	4.9
  median time (hours)	0.5	2.4	1.8	4.7
  25% took more than	0.7	3.0	2.0	5.7
  10% took more than	0.8	3.0	3.0	6.8

• How to Start PS6

  • Follow the instructions in the GDoc CS251-F20-T2 Pset Submission Instructions for creating your PS6 Google Doc. Put all written answers and a copy of all code into this PS6 GDoc. If you are working with a partner, only one of you needs to create this document, but you should link it from both of your List Docs.

• Submission:

  • For all parts of all problems, include all answers (including Racket and SML code) in your PS6 google doc. Format Racket and SML code using a fixed-width font, like Consolas or Courier New. You can use a small font size if that helps.
  • For Problem 1:
    • Be sure that your deep-reverse definition in yourAccountName-ps6-deep-reverse.rkt also appears in your PS6 GDoc.
    • Drop a copy of your yourAccountName-ps6-deep-reverse.rkt in your ~/cs251/drop/ps06 drop folder on cs.wellesley.edu.
  • For Problem 2:
    • Be sure that the definitions of the four functions desugar-and, desugar-let*, desugar-cond, and desugar-begin in yourAccountName-ps6-desugaring.rkt also appears in your PS6 GDoc.
    • Drop a copy of your yourAccountName-ps6-desugaring.rkt in your ~/cs251/drop/ps06 drop folder on cs.wellesley.edu.
  • For Problem 3:
    • Include the modified parts of yourAccountName-ps6-postfix.rkt in your PS6 GDoc. (You only need to include the modified parts, not the entire contents of the PostFix interpreter!)
    • Drop a copy of your yourAccountName-ps6-postfix.rkt in your ~/cs251/drop/ps06 drop folder on cs.wellesley.edu.
  • For Problem 4:
    • For parts a, b, and d, include a single AST for P_Intex (from part a) that is annotated with depth information (from part b) and stack information (from part d).
    • For part c, include the commented PostFix program P_PostFix that is the result of translating P_Intex to PostFix.
  • For Problem 5 (all instructions below are new:.
    • For Part a:
      • Include the definition of eval and any helper functions in your PS6 GDoc.

      • Drop a copy of your ~/cs251/sml/ps6/yourAccountName-Condex.sml file in your ~/cs251/drop/ps06 drop folder on cs.wellesley.edu by executing the following (replacing all three occurrences of gdome by your cs server username):

        scp -r ~/cs251/sml/ps6/gdome-Condex.sml gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps06

    • For Part b, include the annotated PostFix program that should result from compiling lec30Test.cdx, along with the sequence of all intermediate stacks when executing the PostFix program on the two given argument sequences.

    • For Part c:
      • Include the definition of expToCmds and any helper functions in your PS6 GDoc.

      • Drop a copy of your ~/cs251/sml/ps6/yourAccountName-CondexToPostFix.sml file in your ~/cs251/drop/ps06 drop folder on cs.wellesley.edu by executing the following (replacing all three occurrences of gdome by your cs server username):

        scp -r ~/cs251/sml/ps6/gdome-CondexToPostFix.sml gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps06

1. Deep Reverse (8 points)

We saw in Lec 26 tree recursion on trees represented as s-expressions could be expressed rather elegantly. (See slides 11 & 12 of the Lec 26 slides as well as the video segments on s-expressions and functions on them, the sexp-atoms exercise, and the sexp-height exercise.)

For example:

(define (atom? x)
  (or (number? x) (boolean? x) (string? x) (symbol? x)))

(define (sexp-num-atoms sexp)
  (if (atom? sexp)
      1
      (foldr + 0 (map sexp-num-atoms sexp))))

> (sexp-num-atoms '((a (b c) d) e (((f) g h) i j k)))
11
> (sexp-num-atoms '(a b c d))
4
> (sexp-num-atoms 'a)
1
> (sexp-num-atoms '())
0

(define (sexp-atoms sexp)
  (if (atom? sexp)
      (list sexp)
      (foldr append null (map sexp-atoms sexp))))

> (sexp-atoms '((a (b c) d) e (((f) g h) i j k)))
'(a b c d e f g h i j k)
> (sexp-atoms '(a b c d))
'(a b c d)
> (sexp-atoms 'a)
'(a)
> (sexp-atoms '())
'()

In this problem, you will define a function (deep-reverse sexp) that returns a new s-expression in which the order of the children at every node of the s-expression tree sexp is reversed.

> (deep-reverse '((a (b c) d) e (((f) g h) i j k)))
'((k j i (h g (f))) e (d (c b) a))
> (deep-reverse '(a b c d))
'(d c b a)
> (deep-reverse 'a)
'a
> (deep-reverse '())
'()

Notes:

• Begin with this starter file ps6-deep-reverse-starter.rkt, which you should rename to yourAccountName-ps6-deep-reverse.rkt. Add your definition of deep-reverse to this file.

• Your definition should have form similar to the definitions for sexp-num-atoms and sexp-atoms, but you’ll want to use something other than foldr.

• You are not allowed to use reverse in your definition.

2. Desugaring Racket (25 points)

How to Start this Problem

Start this problem by copying the ps6-desugaring-starter.rkt file into Racket, and renaming the file to yourAccountName-ps6-desugaring.rkt.

As you read the following subsections, you may wish to experiment with some of the functions they describe, all of which are in yourAccountName-ps6-desugaring.rkt.

As explained later in the Your Task section, your objective in this problem is to define several one-step desugaring rewrite functions.

Although the explanation for this problem is very long, what you are asked to do is fairly straightforward. The main purpose of this problem is to teach you about how desugaring works, which is a nice illustration of the metalanguage theme of this problem set. After doing this problem, you should have a much better understanding how desugaring works in Racket and other languages.

Background

We have seen that Racket has just a few kernel constructs: (define Id_name E_defn), identifiers, literals (number, booleaans, strings), if lambda, letrec, quote, and function calls.

Other Racket constructs are transformed into kernel constructs by a rewriting process called desugaring. Here are some of the desugaring rewrite rules we have seen:

(define (Id_fun Id_param_1 ... Id_param_n) E_body) 
=> (define Id_fun (lambda Id_param_1 ... Id_param_n) E_body)

(let {[Id_name_1 E_defn_1] ... [Id_name_n E_defn_n]} E_body)
=> ( (lambda (Id_name_1 ... Id_name_n) E_body)
      E_defn_1 ... E_defn_n)

(let* {} E_body) => E_body
(let* {[Id_name_1 E_defn_1] ...} E_body)
=> (let {[Id_name_1 E_defn_1]} 
     (let* {...} E_body))

In a previous version of this pset description, the above (let* {...} E_body)) incorrectly had let rather than let*.

(and) => #t
(and E_conjunct) => E_conjunct
(and E_conjunct_1 ...) => (if E_conjunct_1 (and ...) #f)

(or) => #f
(or E_disjunct) => E_disjunct
(or E_disjunct_1 ...) => (let {[Id_fresh E_disjunct_1]}
                           (if Id_fresh Id_fresh (or ...)))
                           ; where Id_fresh is a ``fresh'' identifier
                           ; not use elsewhere in the program 

(begin E_sequent) => E_sequent ; Must have at least one sequent
(begin E_sequent_1 ...) => (let {[Id_fresh E_sequent_1]}
                             (begin ...))
                           ; where Id_fresh is a ``fresh'' identifier
                           ; not use elsewhere in the program 

(cond (else E_body)) => E_body
(cond (E_test_1 E_body_1) ...) => (if E_test_1 E_body_1 (cond ...)

In the above rules, the ellipses ... stand for one or more copies of the previous phrase. E.g. (and E_conjunct_1 ...) refers to an and expression with at least one subexpressions (called conjuncts); E_conjunct_1 is the first conjunct, and ... stands for the rest of the conjuncts following E_conjunct_1.

Note some features of these rules:

• The desugaring of many constructs is defined in terms of one or more base cases and a transformation to a ``smaller” version of the construct. So the rules may need to be applied many times to complete the desugaring. For example:

  (and (< a b) (< b c) (< c d))
  => ; desugaring rule for (and (a < b) ...) 
  (if (< a b)  
      (and (< b c) (< c d))
      #f)
  => ; desugaring rule for (and (b < c) ...) 
  (if (< a b)  
      (if (< b c) 
          (and (< c d))
               #f)
          #f)
  => ; desugaring rule for (and (c < d))
  (if (< a b)  
      (if (< b c) 
          (< c d)
          #f)
      #f)

• Some sugar constructs desugar into other sugar constructs that must themselves be desugared. For example:

  (let* {[a (+ x 1)] 
         [b (* a a)]} 
    (list a b))
  => ; desugaring rule for (let* {[a (+ x 1)] ...} (list a b))
  (let {[a (+ x 1)]}
   (let* {[b (* a a)]} 
     (list a b))) 
  => ; desugaring rule for (let {[a (+ x 1)]} ...)
   (let* {[b (* a a)]} 
  ((lambda (a) 
     (let* {[b (* a a)]} 
       (list a b)))
   (+ x 1))
  => ; desugaring rule for (let* {[b (* a a)] ...} (list a b))
  ((lambda (a) 
     (let {[b (* a a)]} 
       (let* {} (list a b))))
   (+ x 1))
  => ; desugaring rule for (let {[b (* a a)]} ...) 
  ((lambda (a) 
     ((lambda (b)
        (let* {} (list a b)))
      (* a a)))
   (+ x 1))
  => ; desugaring rule for (let* { } (list a b))
  ((lambda (a) 
     ((lambda (b)
        (list a b))
      (* a a)))
   (+ x 1))

• Some desugaring need to introduce ``fresh” identifiers that are not used elsewhere in the program. For simplicity, we will imagine that all fresh identifiers have the form id.posint, where posint is a positive integer, e.g. id.1, id.2, etc., and that programmers do not use identifiers of this form in their programs. For example:

  (or (< a b) (< b c) (< c d))
  => ; desugaring rule for (or (< a b) ...)
  (let {[id.1 (< a b)]} ; id.1 is a fresh identifier
    (if id.1 
        id.1
        (or (< b c) (< c d))))
  => ; desugaring rule for (let {[id.1 (< a b)]} ...)
  ((lambda (id.1)
     (if id.1 
         id.1
         (or (< b c) (< c d))))
   (< a b))
  => ; desugaring rule for (or (< b c) ...)
  ((lambda (id.1)
     (if id.1 
         id.1
         (let {[id.2 (< b c)]} ; id.2 is a fresh identifier
           (if id.2
               id.2
               (or (< c d))))))
   (< a b))
  => ; desugaring rule for (let {[id.2 (< b c)]} ...)
  ((lambda (id.1)
     (if id.1 
         id.1
         ((lambda (id.2)
             (if id.2
                 id.2
                 (or (< c d))))
          (< b c))))
   (< a b))
  => ; desugaring rule for (or (< c d))
  ((lambda (id.1)
     (if id.1 
         id.1
         ((lambda (id.2)
             (if id.2
                 id.2
                 (< c d)))
          (< b c))))
   (< a b))

Expressing desugaring rewrite rules as Racket functions that transform s-expressions

The desugaring rewrite rules presented above can be implemented in Racket as transformations on s-expressions that represent Racket syntax. For example, the rule

(let {[Id_name_1 E_defn_1] ... [Id_name_n E_defn_n]} E_body)
=> ( (lambda (Id_name_1 ... Id_name_n) E_body)
      E_defn_1 ... E_defn_n)

can be implemented by the following desugar-let function:

(define (desugar-let sexp)
  (make-call (make-lambda (let-names sexp)
                          (let-body sexp))
             (let-defns sexp)))

(This and all functions mentioned in this problem can be found in yourAccountName-ps6-desugaring.rkt.)

The desugar-let function uses some of the following syntactic abstractions for let, lambda, and function call expressions:

;;----------------------------------------
;; let expressions have the form 
;;   (let {[Id_name_1 Id_defn_1] 
;;         ... 
;;         [Id_name_n Id_defn_n]} 
;;     E_body)
;; where n >= 0

(define (make-let names defns body)
  (if (and (forall? symbol? names)
           (= (length names) (length defns)))
      (list 'let
            (map (λ (name defn) (list name defn)) names defns)
            body)
      (error "make-let: malformed let parts"
             (list 'let names defns body))))

(define (let-bindings sexp) (second sexp))
(define (let-names sexp) (map first (let-bindings sexp)))
(define (let-defns sexp) (map second (let-bindings sexp)))
(define (let-body sexp) (third sexp))
  
(define (let? sexp)
  (and (list? sexp)
       (= (length sexp) 3)
       (eq? (first sexp) 'let)
       (list (second sexp)) ; must be a list of bindings
       (forall? binding? (second sexp))))

(define (binding? sexp) ; name/defn binding, e.g. '(sqr (* a a))
  (and (list? sexp)
       (= (length sexp) 2)
       (symbol? (first sexp))))

;;----------------------------------------
;; lambda expressions have the form 
;;   (lambda (Id_param_1 ... Id_param_n) E_body)
;; where n >= 0

(define (make-lambda params body)
  (if (forall? symbol? params)
      (list 'lambda params body)
      (error "make-lambda: params aren't all symbols" params)))
(define (lambda-params sexp) (second sexp))
(define (lambda-body sexp) (third sexp))

(define (lambda? sexp)
  (and (list? sexp)
       (= (length sexp) 3)
       (eq? (first sexp) 'lambda)
       (list? (second sexp))
       (forall? symbol? (second sexp))))

;;----------------------------------------
;; function calls have the form 
;;   (E_rator E_rand_1 ... E_rand_n)
;; where n >= 0

(define (make-call rator rands)
  (if (memq rator '(and begin cond define if lambda
                    let let* letrec or quote))
      (error "make-call: function calls can't begin with core or sugar keyword"
             rator)
      (cons rator rands)))
  
(define (call-rator sexp) (first sexp))
(define (call-rands sexp) (rest sexp))

(define (call? sexp)
  (and (list? sexp)
       (>= (length sexp) 1)
       ;; Function calls can't begin with core or sugar keyword
       (not (memq (first sexp) '(and begin cond define if lambda
                                 let let* letrec or quote)))
       ))

Similarly, the three desugaring rules for transforming or expressions

(or) => #f
(or E_disjunct) => E_disjunct
(or E_disjunct_1 ...) => (let {[Id_fresh E_disjunct_1]}
                           (if Id_fresh Id_fresh (or ...)))
                           ; where Id_fresh is a ``fresh'' identifier
                           ; not use elsewhere in the program 

can be implemented by the following desugar-or function

(define (desugar-or sexp)
  (let {[disjuncts (or-disjuncts sexp)]}
    (cond ((null? disjuncts)
           ;; (or) => #f
           #f)
          ((= (length disjuncts) 1)
           ;; (or E) => E
           (first disjuncts))
          (else
           ;; (or E ...) => (let {[Id_fresh E]}
           ;;                 (if Id_fresh Id_fresh (or ...))) 
           (let {[fresh (fresh-identifier)]} ;; name fresh identifier so that
                                             ;; same identifier is use multiple times
             (make-let (list fresh) ; list of one identifier
                       (list (first disjuncts)) ; list of one defn exp
                       (make-if fresh
                                fresh
                                (make-or (rest disjuncts))))))
          )))

where desugar-or uses some new syntactic abstractions:

;;----------------------------------------
;; or expressions have the form 
;;   (or E_disjunct_1 ... E_disjunct_n)
;; where n >= 0

(define (make-or disjuncts) (cons 'or disjuncts))
(define (or-disjuncts sexp) (rest sexp))
(define (or? sexp)
  (and (list? sexp)
       (>= (length sexp) 1)
       (eq? (first sexp) 'or)))

The desugar-or function also uses the nullary function fresh-identifier, which returns a new fresh identifier each time it is called:

> (fresh-identifier)
'id.1

> (fresh-identifier)
'id.2

> (fresh-identifier)
'id.3

A desugar function for desugaring Racket epxressions represented as s-expressions

The desugaring rewrite rules presented above just perform one step of the rewriting process. Potentially, such rules may need to be applied many times on many parts of an s-expression in order to completely desugar it.

This processes uses the helper function desugar-rewrite-one-step, which attempts to apply one desugaring rewrite rule step to the given s-expression sexp:

;;----------------------------------------
;; desugar-rewrite-one-step dispatches to a 
;; specialized function for each sugar construct. 
;;
(define (desugar-rewrite-one-step sexp)
  (cond ((definition? sexp) (desugar-definition sexp))
        ((let? sexp) (desugar-let sexp))
        ((let*? sexp) (desugar-let* sexp))
        ((cond? sexp) (desugar-cond sexp))
        ((begin? sexp) (desugar-begin sexp))
        ((and? sexp) (desugar-and sexp))
        ((or? sexp) (desugar-or sexp))
        (else sexp) ; otherwise return expression unchanged
        ))

desugar-rewrite-one-step just determines if sexp is a sugar construct that can be rewritten.

• If so, it calls the appropriate function for rewriting that construct, such as the desugar-let or desugar-or constructs shown above.

• If not, it simply returns sexp unchanged.

For example:

> (desugar-rewrite-one-step '(let {[sum (+ a b)] [diff (- a b)]} (/ sum diff)))
'((lambda (sum diff) (/ sum diff)) (+ a b) (- a b)) 
; complete desugaring in one step

> (desugar-rewrite-one-step '(or (< a b) (< b c) (< c d)))
'(let ((id.1 (< a b))) (if id.1 id.1 (or (< b c) (< c d))))
; partial desugaring in one step

> (desugar-rewrite-one-step '(+ x (* y z)))
'(+ x (* y z)) 
; unchanged sexp; no desugaring possible

The desugar function applies desugar-rewrite-one-step as many times as necessary on an s-expression (and it subtrees) in order to completely transform it by all the desugaring rules:

(define (desugar sexp)
  (let {[dsexp (desugar-rewrite-one-step sexp)]} ; dsexp is the desugared sexp
    (if (not (equal? dsexp sexp))
        ;; then case: a desugaring rewrite rule transformed the top-level sexp 
        ;; to dsexp; iteratively apply desugaring rewrite rules to dsexp
        (desugar dsexp))
        ;; else case: desugaring rules didn't change the top-level sexp,
        ;; so it must be a kernel sexp; now apply desugaring rules to
        ;; subtrees of the kernel sexp
        (cond ((literal? dsexp) dsexp)
              ((identifier? dsexp) dsexp)
              ((definition? dsexp)
               (make-definition (definition-name-part dsexp)
                                (desugar (definition-defn dsexp))))
              ((if? dsexp)
               (make-if (desugar (if-test dsexp))
                        (desugar (if-then dsexp))
                        (desugar (if-else dsexp))))
              ((lambda? dsexp)
               (make-lambda (lambda-params dsexp)
                            (desugar (lambda-body dsexp))))
              ((call? dsexp)
               (make-call (desugar (call-rator dsexp))
                          (map desugar (call-rands dsexp))))
              ((letrec? dsexp)
               (make-letrec (letrec-names dsexp)
                            (map desugar (letrec-defns dsexp))
                            (desugar (letrec-body dsexp))))
              (else (error "Unhandled expression" dsexp))
              ))))

desugar first applies desugar-rewrite-one-step on the given s-expression sexp to yield dsexp.

• If dsexp is different from sexp, it is iteratively desugared by calling desugar on dsexp. This handles cases like desugaring or, which yields a let expression that itself needs to be desugared.

• If dsexp is the same as sexp, then the desugaring rules have not made any transformations to the whole s-expression sexp. This means it must be a kernel expression. But it might still be necessary to desugar the subtrees of this kernel expression. For example, this conditional expression has parts that need desugaring:

  (if (or (< a b) (< b c)) (* a b) (let {[c (+ a b)]} (* c c)))

  So desugar is recursively applied to each of the subtrees of the kernel expression.

  The base cases of this recursive processing are the leaves of kernel expresssions — i.e., identifiers (variable references) and literal values (numbers, booleans, strings, and quoted symbols/lists). These leaves are unchanged by the desugaring process

Here’s some examples of desugar in action:

> (desugar '(let {[sum (+ a b)] [diff (- a b)]} (/ sum diff)))
'((lambda (sum diff) (/ sum diff)) (+ a b) (- a b)) 
; performed just one rewrite step to complete desugaring

> (desugar '(or (< a b) (< b c) (< c d)))
'((lambda (id.1) (if id.1 id.1 ((lambda (id.2) (if id.2 id.2 (< c d))) (< b c)))) (< a b))
; performed many rewrite steps to complete desugaring

> (desugar '(if (or (< a b) (< b c)) (* a b) (let {[c (+ a b)]} (* c c))))
'(if ((lambda (id.2) (if id.2 id.2 (< b c))) (< a b)) (* a b) ((lambda (c) (* c c)) (+ a b)))
; performed rewrite steps on then and else clauses of `if` to complete desugaring

> (desugar '(+ x (* y z)))
'(+ x (* y z)) 
; performed no rewrite steps

In order to help you understand the step-by-step rewriting nature of the desugaring rewrite rules, in the case where dsexp is not equal to sexp, the desugar function displays some tracing information if the flag show-one-step-desugarings? is #t:

(define show-one-step-desugarings? #t) ; controls tracing within desugar

(define (desugar sexp)
  (let {[dsexp (desugar-rewrite-one-step sexp)]} ; dsexp is the desugared sexp
    (if (not (equal? dsexp sexp))
        ;; then case: a desugaring rewrite rule transformed the top-level sexp 
        ;; to dsexp; iteratively apply desugaring rewrite rules to dsexp
        (begin (if show-one-step-desugarings?
                   ;; show details of one-step rewriting in this case
                   (begin (printf "desugar-rewrite-one-step:\n")
                          (pretty-display sexp)
                          (printf "=> ")
                          (pretty-display dsexp)
                          (printf "\n"))
                   'do-nothing)   
               (desugar dsexp))
        ;; else case is unchanged from above

Below are the above examples of desugar with show-one-step-desugarings? turned on:

> (desugar '(let {[sum (+ a b)] [diff (- a b)]} (/ sum diff)))
desugar-rewrite-one-step:
(let ((sum (+ a b)) (diff (- a b))) (/ sum diff))
=> ((lambda (sum diff) (/ sum diff)) (+ a b) (- a b))

'((lambda (sum diff) (/ sum diff)) (+ a b) (- a b))

> (desugar '(or (< a b) (< b c) (< c d)))
desugar-rewrite-one-step:
(or (< a b) (< b c) (< c d))
=> (let ((id.3 (< a b))) (if id.3 id.3 (or (< b c) (< c d))))

desugar-rewrite-one-step:
(let ((id.3 (< a b))) (if id.3 id.3 (or (< b c) (< c d))))
=> ((lambda (id.3) (if id.3 id.3 (or (< b c) (< c d)))) (< a b))

desugar-rewrite-one-step:
(or (< b c) (< c d))
=> (let ((id.4 (< b c))) (if id.4 id.4 (or (< c d))))

desugar-rewrite-one-step:
(let ((id.4 (< b c))) (if id.4 id.4 (or (< c d))))
=> ((lambda (id.4) (if id.4 id.4 (or (< c d)))) (< b c))

desugar-rewrite-one-step:
(or (< c d))
=> (< c d)

'((lambda (id.3) (if id.3 id.3 ((lambda (id.4) (if id.4 id.4 (< c d))) (< b c)))) (< a b))
>

> (desugar '(if (or (< a b) (< b c)) (* a b) (let {[c (+ a b)]} (* c c))))
desugar-rewrite-one-step:
(or (< a b) (< b c))
=> (let ((id.5 (< a b))) (if id.5 id.5 (or (< b c))))

desugar-rewrite-one-step:
(let ((id.5 (< a b))) (if id.5 id.5 (or (< b c))))
=> ((lambda (id.5) (if id.5 id.5 (or (< b c)))) (< a b))

desugar-rewrite-one-step:
(or (< b c))
=> (< b c)

desugar-rewrite-one-step:
(let ((c (+ a b))) (* c c))
=> ((lambda (c) (* c c)) (+ a b))

'(if ((lambda (id.5) (if id.5 id.5 (< b c))) (< a b)) (* a b) ((lambda (c) (* c c)) (+ a b)))
>

> (desugar '(+ x (* y z)))
'(+ x (* y z)) ; desugar-rewrite-one-step doesn't change any s-expressions in this example

Your task

The file yourAccountName-ps6-desugaring.rkt that you copied from the ps6-desugaring-starter.rkt file contains all the code describe above.

It includes correct implementations of the the following functions for one-step desugaring rewriting rules that are used in desugar-rewrite-one-step:

• desugar-definition
• desugar-let
• desugar-or

Your goal is to flesh out the skeletons for the other four desugaring functions (shown below) so that they correctly express the associated rewrite rules. These skeletons appear in yourAccountName-ps6-desugaring.rkt below this header:

;;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
;; FOR PS6 PROBLEM 2, WRITE YOUR SOLUTIONS BELOW:
;;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

• desugar-and

  ;; desugar-and should implement these three desugaring rules
  ;;
  ;; 1. (and) => #t
  ;;
  ;; 2. (and E) => E
  ;; 
  ;; 3. (and E ...) => (if E (and ...) #f) 
  ;;
  (define (desugar-and sexp)
    'flesh-out-desugar-and)

  Some examples:

  > (desugar-and '(and))
  #t
  
  > (desugar-and '(and (< a b)))
  '(< a b)
  
  > (desugar-and '(and (< a b) (< b c) (< c d)))
  '(if (< a b) (and (< b c) (< c d)) #f)

  Notes:

  • You should not use the and? predicate in desugar-and. The argument sexp to desugar-and is already guaranteed to be an and s-expression because (desugar-and sexp) is called by desugar-rewrite-one-step only in the case where (and? sexp) is true.

  • You should call the syntax functions and-conjuncts, make-if, and make-and in the body of desugar-and.

    • and-conjuncts returns the list of subexpressions of the and construct, which are known as conjuncts.

    • You should use the usual list operations null?, first, rest, and length to manipulate the list of conjuncts.

  • You can test all 3 above cases using (test-desugar-and).

• desugar-let*

  ;; desugar-let* should implement these two desugaring rules
  ;;
  ;; 1. (let* { } Ebody) => Ebody
  ;;
  ;; 2. (let* {[Id1 E1] ...} Ebody)
  ;;    => (let {[Id1 E1]}
  ;;         (let* {...} Ebody))
  ;; 
  (define (desugar-let* sexp)
    'flesh-out-desugar-let*)

  Some examples:

  > (desugar-let* '(let* {} (list a b)))
  '(list a b)
  
  > (desugar-let* '(let* {[b (* a a)]} (list a b)))
  '(let ((b (* a a))) (let* () (list a b)))
  
  > (desugar-let* '(let* {[a (+ x 1)] [b (* a a)]} (list a b)))
  '(let ((a (+ x 1))) (let* ((b (* a a))) (list a b)))

  Note:

  • You should not use the let*? predicate in desugar-let*. The argument sexp to desugar-let* is already guaranteed to be a let* s-expression because (desugar-let* sexp) is called by desugar-rewrite-one-step only in the case where (let*? sexp) is true.

  • You should call the syntax functions let*-names, let*-defns, let*-body, make-let, and make-let*.

    • Both let*-names and let*-defns return lists that you should manipulate via the usual list operations null?, first, and rest.

    • Both make-let and make-let* expect their first and second arguments (names and defns, respectively) to be lists.

  • You can test all 3 above cases using (test-desugar-let*).

• desugar-cond

  ;; desugar-cond should implement these two desugaring rules
  ;;
  ;; 1. (cond (else E)) => E
  ;;
  ;; 2. (cond (Etest Ebody) ...) => (if Etest Ebody (cond ...))
  ;; 
  (define (desugar-cond sexp)
    'flesh-out-desugar-cond)

  Some examples (you can test all 3 cases using (test-desugar-cond)):

  > (desugar-cond '(cond (else (- a b))))
  '(- a b)
  
  > (desugar-cond '(cond ((= a b) (* a b)) (else (- a b))))
  '(if (= a b) (* a b) (cond (else (- a b))))
  
  > (desugar-cond '(cond ((< a b) (+ a b)) ((= a b) (* a b)) (else (- a b))))
  '(if (< a b) (+ a b) (cond ((= a b) (* a b)) (else (- a b))))

  Notes:

  • You should not use the cond? predicate in desugar-cond. The argument sexp to desugar-cond is already guaranteed to be a cond s-expression because (desugar-cond sexp) is called by desugar-rewrite-one-step only in the case where (cond? sexp) is true.

  • You should not use the cond-clauses? predicate in desugar-cond. This is just a helper function used in the definitions of cond? of make-cond.

  • You should call the syntax functions cond-clauses, make-if, and make-cond.

    • cond-clauses returns a list of all clauses of the cond construct. You should manipulate this list of clauses via the usual list operations length, first, and rest.

    • The two parts of each clause (known as the test and body) should be accessed using the syntax functions cond-clause-test and cond-clause-body.

    • The syntactic abstractions for cond guarantee that it has at least one clause, and that the last clause must have a test part that is else. So you don’t need to check that the clauses are nonempty, and you don’t need to check that the test part of clause is else when there’s only one clause.

  • You can test all 3 above cases using (test-desugar-cond).

• desugar-begin

  ;; desugar-begin* should implement these two desugaring rules
  ;;
  ;; 1. (begin E) => E
  ;;
  ;; 2. (begin E1 ...) => (let {[Id_fresh E1]} (begin ...)
  ;;    ;; Note: use (fresh-identifier) to generate Id_fresh
  ;;
   (define (desugar-begin sexp)
    'flesh-out-desugar-begin)

  Some examples (you can test all 3 cases using (test-desugar-begin)):

  > (desugar-begin '(begin (+ x y)))
  '(+ x y)
  
  > (desugar-begin '(begin (printf "y is ~a\n" y) (+ x y))) 
  '(let ((id.1 (printf "y is ~a\n" y))) (begin (+ x y))) 
  ; Your fresh id might differ
  
  > (desugar-begin '(begin (printf "x is ~a\n" x) (printf "y is ~a\n" y) (+ x y))) 
  '(let ((id.2 (printf "x is ~a\n" x))) (begin (printf "y is ~a\n" y) (+ x y)))
  ; Your fresh id might differ

  Notes:

  • You should not use the begin? predicate in desugar-begin. The argument sexp to desugar-begin is already guaranteed to be a begin s-expression because (desugar-begin sexp) is called by desugar-rewrite-one-step only in the case where (begin? sexp) is true.

  • You should call the syntax functions begin-sequents, make-let, make-begin, and fresh-identifier.

    • begin-sequents returns a list of all subexpressions of the begin construct, which are known as sequents You should manipulate this list of sequents via the usual list operations length, first, and rest.

    • The syntactic abstractions for begin guarantee that it has at least one sequent, so you don’t need to check that the sequents are nonempty

    • Recall from above that the first two arguments (names and defns) of make-let must be lists.

    • As illustrated in desugar-or, use the call (fresh-identifier) to generate a fresh-identifier. Because the call (fresh-identifier) is stateful and generates a different new fresh identifier every time it is called, your test cases might have different fresh identifiers than in the above examples.

  • You can test all 3 above cases using (test-desugar-begin).

General Notes:

• In all your definitions, you should use apppropriate syntactic abstractions, which are defined in the section of yourAccountName-ps6-desugaring.rkt that begins:

  ;;;****************************************************************************
  ;;; Syntactic abstractions

• Carefully study the working functions desugar-let and desugar-or as examples of one-step desugaring rewrite rules.

• Use (test-all) to run all testers for this problem.

• A beautiful aspect of this desugaring framework is that, once your one-step desugaring rewrite functions are working, the desugar function can use them to completely desugar any s-expresions containing them, possibly used together with other sugar constructs. For example:

  ;; These examples are shown with (define show-one-step-desugarings? #f)
  ;; but you can try them with this flag set to #t
  
  > (desugar '(and (< a b) (< b c) (< c d)))
  '(if (< a b) (if (< b c) (< c d) #f) #f)
  
  > (desugar '(let* {[a (+ x 1)] [b (* a a)]} (list a b)))
  '((lambda (a) ((lambda (b) (list a b)) (* a a))) (+ x 1))
  
  > (desugar '(cond ((< a b) (+ a b)) ((= a b) (* a b)) (else (- a b))))
  '(if (< a b) (+ a b) (if (= a b) (* a b) (- a b)))
  
  > (desugar '(begin (printf "x is ~a\n" x) (printf "y is ~a\n" y) (+ x y)))
  '((lambda (id.2) ((lambda (id.3) (+ x y)) (printf "y is ~a\n" y))) (printf "x is ~a\n" x))

  desugar should even work on large s-expresions that combine all seven syntactic sugar constructs, like this one:

  (define big-sexp
    '(define (test-repl prompt done)
       (begin (printf "~a x>" prompt)
              (let {[x (read)]}
                (if (equal? x done)
                    'repl-done
                    (begin (printf "~a y>" prompt)
                           (let* {[y (read)]
                                  [result
                                   (cond ((or (< x y)
                                              (> y 100) 
                                              (and (< 10 x)
                                                   (< y (* 2 x))
                                                   (< y 50)))
                                          (let* {[a (+ x y)]
                                                 [b (* x a)]
                                                 [c (/ a b)]}
                                            (list x y a b c)))
                                         ((and (> x y) (> (* 3 x) y))
                                          (list x y (* y y)))
                                         (else (list x y)))]}
                             (begin (printf "Result is ~a\n" result)
                                    (test-repl prompt done)))))))))
  
  (desugar big-sexp)
  '(define test-repl ; this s-expression was manually reformatted by Lyn to be more readable
      (lambda (prompt done)
        ((lambda (id.1)
           ((lambda (x)
              (if (equal? x done)
                'repl-done
                ((lambda (id.2)
                   ((lambda (y)
                      ((lambda (result) 
                         ((lambda (id.3) (test-repl prompt done)) 
                          (printf "Result is ~a\n" result)))
                       (if ((lambda (id.4) 
                              (if id.4 id.4 ((lambda (id.5) 
                                               (if id.5 id.5 (if (< 10 x) 
                                                                 (if (< y (* 2 x)) 
                                                                     (< y 50) #f) 
                                                                     #f))) 
                                             (> y 100))))
                            (< x y))
                         ((lambda (a) ((lambda (b) ((lambda (c) 
                                                      (list x y a b c)) 
                                                    (/ a b))) 
                                       (* x a)))
                          (+ x y))
                         (if (if (> x y) (> (* 3 x) y) #f) 
                             (list x y (* y y)) 
                             (list x y)))))
                    (read)))
                 (printf "~a y>" prompt))))
            (read)))
         (printf "~a x>" prompt))))

  Since big-sexp and the result of desugaring it are both s-expressions for Racket function definitions, you can remove the quote mark on them, and give them as inputs to the Racket interpreter to define a function test-repl. You can then verify that the behavior of the function before and after desugaring is the same!

3. Extending PostFix (34 points)

In lecture we studied several different versions of an interpreter for the PostFix language implemented in Racket. (See the materials from Lec 28 and Lec 29, especially the slides for the PostFix Interpreter in Racket and the associated videos.)

This problem involves starting with the following version of the interpreter:

• ps6-postfix-starter.rkt

This is a slightly modified version of the file postfix-transform-fancy.rkt studied in lecture.

Begin by making a copy of ps6-postfix-starter.rkt named yourAccountName-ps6-postfix.rkt and load this into Dr. Racket. Near the bottom of this file is the following PostFix program named sos (for “sum of squares”). Racket’s semi-colon comments have been used to explain the commands in the program:

;; Sum-of-squares program 
(define sos
  '(postfix 2 ; let's call the arguments a and b, from top down
            1 nget ; duplicate a at top of stack
            mul ; square a
            swap ; stack now has b and a^2 from top down
            1 nget mul ; square b
            add ; add b^2 + a^2 and return
            ))

Let’s run the program on the arguments 5 and 12:

> (postfix-run sos '(5 12))
About to execute commands (1 nget mul swap 1 nget mul add) on stack (5 12)
  after executing 1, stack is (1 5 12)
  after executing nget, stack is (5 5 12)
  after executing mul, stack is (25 12)
  after executing swap, stack is (12 25)
  after executing 1, stack is (1 12 25)
  after executing nget, stack is (12 12 25)
  after executing mul, stack is (144 25)
  after executing add, stack is (169)
169

Note that the stack that results from executing each command on the previous stack is displayed, line by line. This behavior is controlled by the display-steps? flag at the top of the program:

(define display-steps? #t)

If we set the flag to #f, the intermediate stack display will be turned off:

(define display-steps? #f)

> (postfix-run sos '(5 12))
169

Turn the display-steps? flag on when it’s helpful to understand or debug a PostFix program.

1. (10 points)

   Consider the following Racket function g that is defined near the bottom of the PostFix interpreter file:

   (define (g a b c)
     (- c
        (if (= 0 (remainder a 2))
            (quotient b (- a c))
            (* (+ b c) a))))

   In this part, your goal is to flesh out the definition of a three-argument PostFix program pfg that performs the same calculation as g on three arguments:

   (define pfg
      '(postfix 3 
          ;; Flesh out and comment the commands in this PostFix program 
        ))

   Here are some examples with a correctly defined pfg:

   > (apply g '(10 2 8))
   7
   
   > (postfix-run pfg '(10 2 8))
   7
   
   > (apply g '(-7 2 3))
   38
   
   > (postfix-run pfg '(-7 2 3))
   38
   
   > (apply g '(5 4 5))
   -40
   
   > (postfix-run pfg '(5 4 5))
   -40

   Notes:

   • Please comment the commands in pfg like those in sos.

   • You have been provided with a testing function (test-pfg) that will test your pfg function on 5 sets of arguments:

     ;; Tests on an incorrect definition of pfg: 
     > (test-pfg)
     Testing pfg on (10 2 8): ***different results***
       g: 7
       pfg: -7
     Testing pfg on (11 2 8): ***different results***
       g: -102
       pfg: 102
     Testing pfg on (-6 3 8): ***different results***
       g: 8
       pfg: -8
     Testing pfg on (-7 2 3): ***different results***
       g: 38
       pfg: -38
     Testing pfg on (5 4 5): ***different results***
       g: -40
       pfg: 40
     
     ;; Tests on a correct definition of pfg: 
     > (test-pfg)
     Testing pfg on (10 2 8):  same result for g and pfg = 7
     Testing pfg on (11 2 8):  same result for g and pfg = -102
     Testing pfg on (-6 3 8):  same result for g and pfg = 8
     Testing pfg on (-7 2 3):  same result for g and pfg = 38
     Testing pfg on (5 4 5):  same result for g and pfg = -40

2. (7 points) Extend PostFix by adding the following two commands:

   • exp: given a stack i_base i_expt ... (where i_base and i_expt are integers), replaces i_base and i_expt by the result of raising i_base to the power of i_expt (or 0 if i_expt is negative).

   • chs: given a stack i_n i_k ... (where i_k and i_n are nonnegative integers and i_k <= i_n), replaces i_n and i_k by the value of i_n choose i_k. (See the definition of “choose” notation here). If one or both of i_n and i_k are invalid arguments, displays an error message (sees examples below).

   For example:

   > (postfix-run '(postfix 0 2 3 exp) '())
   8
   
   > (postfix-run '(postfix 0 3 2 exp) '())
   9
   
   > (postfix-run '(postfix 0 5 3 exp) '())
   125
   
   > (postfix-run '(postfix 0 3 5 exp) '())
   243
   
   > (postfix-run '(postfix 0 0 5 exp) '())
   0
   
   > (postfix-run '(postfix 0 5 0 exp) '())
   1
   
   > (postfix-run '(postfix 0 5 -1 exp) '())
   0
   
   > (postfix-run '(postfix 0 3 -5 exp) '())
   0
   
   > (postfix-run '(postfix 0 6 0 chs) '())
   1
   
   > (postfix-run '(postfix 0 6 1 chs) '())
   6
   
   > (postfix-run '(postfix 0 6 2 chs) '())
   15
   
   > (postfix-run '(postfix 0 6 3 chs) '())
   20
   
   > (postfix-run '(postfix 0 6 4 chs) '())
   15
   
   > (postfix-run '(postfix 0 6 5 chs) '())
   6
   
   > (postfix-run '(postfix 0 6 6 chs) '())
   1
   
   > (postfix-run '(postfix 0 6 7 chs) '())
   ERROR: invalid operands for chs (6 7)
   
   > (postfix-run '(postfix 0 6 -2 chs) '())
   ERROR: invalid operands for chs (6 -2)
   
   > (postfix-run '(postfix 0 -6 3 chs) '())
   ERROR: invalid operands for chs (-6 3)

   Notes:

   • Do not modify postfix-exec-command for this part. Instead, just add two bindings to the list postfix-arithops.

   • The Racket built-in expt function is helpful.

   • Use a factorial function (we’ve defined many in class!) to implement chs.

3. (4 points) Extend PostFix by adding the following three commands:

   • le is like lt, but checks “less than or equal to” rather than “less than”
   • ge is like gt, but checks “greater than or equal to” rather than “greater than”
   • and expects two integers at the top of the stack. It replaces them by 0 if either is 0; otherwise it replaces them by 1.

   For example:

   > (postfix-run '(postfix 0 4 5 le) '())
   1
   
   > (postfix-run '(postfix 0 5 5 le) '())
   1
   
   > (postfix-run '(postfix 0 5 4 le) '())
   0
   
   > (postfix-run '(postfix 0 4 5 ge) '())
   0
   
   > (postfix-run '(postfix 0 4 4 ge) '())
   1
   
   > (postfix-run '(postfix 0 5 4 ge) '())
   1
   
   > (postfix-run '(postfix 0 0 0 and) '())
   0
   
   > (postfix-run '(postfix 0 0 1 and) '())
   0
   
   > (postfix-run '(postfix 0 1 0 and) '())
   0
   
   > (postfix-run '(postfix 0 0 17 and) '())
   0
    
   > (postfix-run '(postfix 0 17 0 and) '())
   0
   
   > (postfix-run '(postfix 0 1 1 and) '())
   1
   
   > (postfix-run '(postfix 0 1 17 and) '())
   1
   
   > (postfix-run '(postfix 0 17 17 and) '())
   1
    
   > (postfix-run '(postfix 0 17 23 and) '())
   1

   Notes:

   • Do not modify postfix-exec-command for this part. Instead, just add three bindings to the list postfix-relops.

   • The testing function (test-5c) will test all of le, ge, and and in the context of the single PostFix program test-sorted:

     (define test-sorted '(postfix 3 ; let's call the arguments a, b, and c, from top down
                              2 nget le ; is a <= b?
                              3 nget 3 nget ge ; is c >= b?
                              and ; is a <= b and c >= b?
                              ))
     
     > (test-5c) ; Uses the test-sorted program in its definition 
     Trying test-sorted on (4 5 6): works as expected; result = 1
     Trying test-sorted on (4 5 5): works as expected; result = 1
     Trying test-sorted on (4 4 5): works as expected; result = 1
     Trying test-sorted on (4 4 4): works as expected; result = 1
     Trying test-sorted on (4 6 5): works as expected; result = 0
     Trying test-sorted on (5 6 4): works as expected; result = 0
     Trying test-sorted on (5 4 6): works as expected; result = 0
     Trying test-sorted on (6 5 4): works as expected; result = 0
     Trying test-sorted on (6 4 5): works as expected; result = 0
     Trying test-sorted on (5 5 4): works as expected; result = 0
     Trying test-sorted on (5 4 4): works as expected; result = 0

   • A very common issue students encounter with attempted solutions to and is that they always return 1 in the test cases, even though they have associated them with a Racket function that returns 0 or 1. This issue is rooted in not understanding how the Racket function associated with the relop symbol is proceessed. Here are some questions to ask yourself in order to debug this issues should you encounter it:

     • Study the functions associated with the other relop symbols. What kind of value do they return? Why?

     • What does the function postfix-relop->racket-binop do in the PostFix interpreter implementation?

     A lesson here is that you need to truly understand the code you are modifying before modifying it!

4. (3 points) Extend PostFix with a dup command that duplicates the top element of the stack (which can be either an integer or executable sequence). For example:

   (define sos-dup '(postfix 2 dup mul swap dup mul add))
   
   > (postfix-run sos-dup '(3 4))
   About to execute commands (dup mul swap dup mul add) on stack (3 4)
     after executing dup, stack is (3 3 4)
     after executing mul, stack is (9 4)
     after executing swap, stack is (4 9)
     after executing dup, stack is (4 4 9)
     after executing mul, stack is (16 9)
     after executing add, stack is (25)
   25
   
   (define cmd-dup '(postfix 1 (dup dup mul add swap) dup 3 nget swap exec exec pop))
   
   > (postfix-run cmd-dup '(4))
   About to execute commands ((dup dup mul add swap) dup 3 nget swap exec exec pop) on stack (4)
     after executing (dup dup mul add swap), stack is ((dup dup mul add swap) 4)
     after executing dup, stack is ((dup dup mul add swap) (dup dup mul add swap) 4)
     after executing 3, stack is (3 (dup dup mul add swap) (dup dup mul add swap) 4)
     after executing nget, stack is (4 (dup dup mul add swap) (dup dup mul add swap) 4)
     after executing swap, stack is ((dup dup mul add swap) 4 (dup dup mul add swap) 4)
   About to execute commands (dup dup mul add swap) on stack (4 (dup dup mul add swap) 4)
     after executing dup, stack is (4 4 (dup dup mul add swap) 4)
     after executing dup, stack is (4 4 4 (dup dup mul add swap) 4)
     after executing mul, stack is (16 4 (dup dup mul add swap) 4)
     after executing add, stack is (20 (dup dup mul add swap) 4)
     after executing swap, stack is ((dup dup mul add swap) 20 4)
     after executing exec, stack is ((dup dup mul add swap) 20 4)
   About to execute commands (dup dup mul add swap) on stack (20 4)
     after executing dup, stack is (20 20 4)
     after executing dup, stack is (20 20 20 4)
     after executing mul, stack is (400 20 4)
     after executing add, stack is (420 4)
     after executing swap, stack is (4 420)
     after executing exec, stack is (4 420)
     after executing pop, stack is (420)
   420
   
   > (postfix-run '(postfix 0 dup) '())
   ERROR: dup requires a nonempty stack ()

   Notes:

   • Implement dup by adding a cond clause to postfix-exec-command.

   • Test your dup implementation using the above test cases. Your dup implementation should ensure there is at least one value on the stack, and give an appropriate error message when there isn’t.

5. (10 points) In this part you will extend PostFix with a rot command that behaves as follows.

   • The top stack value should be a positive integer rotlen that we’ll call the rotation length. Assume there are n values v₁, …, v_n below rotlen on the stack, where n is greater than or equal to rotlen. Let’s refer to the first rotlen of these n values as the prefix of the n values, and any remaining values as the suffix of the n values.

   • The result of performing the rot command is to ``rotate’’ the prefix by moving v₁ to the end of the prefix. That is, the value v₁ is moved to index rotlen in the prefix, and each of the values v₂ through v_rotlen is shifted down index (i.e., moved one position to the left) so that they now occupy the indices 1 through rotlen-1. So after rot is performed, the elements of the prefix are v₂ … v_rotlen v₁. For example, if rotlen is 2, then rot acts like swap, and if rotlen is 1, then rot leaves the stack unchanged.

   • The values in the suffix are unchanged by rot.

   • When rotlen is 0, a negative integer, or a noninteger, the rot command signals an error.

   Here are examples involving rot:

   (define rot-test '(postfix 6 4 rot 3 rot 2 rot))
   
   > (postfix-run rot-test '(8 7 6 5 9 10))
   About to execute commands (4 rot 3 rot 2 rot) on stack (8 7 6 5 9 10)
     after executing 4, stack is (4 8 7 6 5 9 10)
     after executing rot, stack is (7 6 5 8 9 10)
     after executing 3, stack is (3 7 6 5 8 9 10)
     after executing rot, stack is (6 5 7 8 9 10)
     after executing 2, stack is (2 6 5 7 8 9 10)
     after executing rot, stack is (5 6 7 8 9 10)
   5
   
   > (postfix-run '(postfix 3 (mul add) rot) '(5 6 7))
   About to execute commands ((mul add) rot) on stack (5 6 7)
     after executing (mul add), stack is ((mul add) 5 6 7)
   ERROR: rot length must be a positive integer but is (mul add)
   
   > (postfix-run '(postfix 3 -1 rot) '(5 6 7))
   About to execute commands (-1 rot) on stack (5 6 7)
     after executing -1, stack is (-1 5 6 7)
   ERROR: rot length must be a positive integer but is -1
   
   > (postfix-run '(postfix 3 4 rot) '(5 6 7))
   About to execute commands (4 rot) on stack (5 6 7)
     after executing 4, stack is (4 5 6 7)
   ERROR: not enough stack values for rot (4 5 6 7)
   
   > (postfix-run '(postfix 0 rot) '())
   About to execute commands (rot) on stack ()
   ERROR: rot requires a nonempty stack but is ()

   Notes:

   • Implement rot by adding a cond clause to postfix-exec-command.

   • Racket supplies a list-tail function that is very helpful for implementing rot:

     > (list-tail '(10 20 30 40 50) 0)
     '(10 20 30 40 50)
     
     > (list-tail '(10 20 30 40 50) 1)
     '(20 30 40 50)
     
     > (list-tail '(10 20 30 40 50) 2)
     '(30 40 50)
     
     > (list-tail '(10 20 30 40 50) 3)
     '(40 50)
     
     > (list-tail '(10 20 30 40 50) 4)
     '(50)
     
     > (list-tail '(10 20 30 40 50) 5)
     '()

     Racket does not provide a similar list-head function, but I have provided it in the ps6-postfix-starter.rkt file. It works this way:

     > (list-head '(10 20 30 40 50) 0)
     '()
     
     > (list-head '(10 20 30 40 50) 1)
     '(10)
     
     > (list-head '(10 20 30 40 50) 2)
     '(10 20)
     
     > (list-head '(10 20 30 40 50) 3)
     '(10 20 30)
     
     >  (list-head '(10 20 30 40 50) 4)
     '(10 20 30 40)
     
     >  (list-head '(10 20 30 40 50) 5)
     '(10 20 30 40 50)

   • Test your rot implementation using the above test cases. Your rot implementation should give appropriate error messages in various situations, like those in the test cases.

4. Static Stack Depth in the Intex-to-PostFix Compiler (21 points)

The intexToPostFix function discussed at the beginning of Thu Dec 10 Lec 32 automatically translates an Intex program to a PostFix program that has the same meaning. (See the fleshed out version of `intexToPostFix` in slide 5 of the Lec 31 Intex solution slides or the file ~/cs251/sml/intex/IntexToPostFix.sml in your csenv application).

The challenging part of this translation is determining the correct index to use for an Nget command when translating an Arg node in an Intext AST.

The key to solving this technical problem is to provide the expToCmds helper function with a depth argument that statically tracks the number of values that have been pushed on the PostFix stack above the argument values at any point of the computation.

The purpose of this problem is for you to study this idea in the context of a particular Intex program so that you better understand it.

1. (3 points) Draw the abstract syntax tree for the following Intex program, which we shall call P_Intex.

   (intex 4 (div (add ($ 1)
                      (mul ($ 2)
                           (sub ($ 3) ($ 4))))
                 (rem (sub (mul ($ 4) ($ 3))
                           ($ 2))
                      ($ 1))))

   For drawing the Intex AST, use the conventions illustrated in slides 3 and 4 of the the Lec 31 Intex slides.

   You may draw the tree by hand or use a drawing program, whichever is easier for you. This will be a wide diagram, so you’ll want to draw it in landscape mode rather than portrait mode. To save space, do not label the edges (i.e., no numargs, body, rator, rand1, rand2, index, or value labels should be used).

   Since you will be annotating this tree with extra information in parts b and d, leave enough room to add some annotations to the right of each node. Here is an example of an annotated node.

   

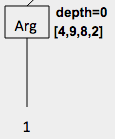
2. (4 points) In your AST for P_Intex from part a, annotate each expression node with the depth associated with that node when it is encountered by the expToCmds function within the intexToPostFix function. As shown above, you should write depth=d to the right of each expression node, where d is the depth of the node.

3. (6 points) Write down the PostFix program that is the result of translating the Intex program P_Intex from part a using the intexToPostFix function. We shall call this program P_PostFix. (You should do this translation by hand, not by running the function in SML.) Important: You translated PostFix code must be exactly the code that would be generated by the intexToPostFix function, not just a PostFix program that happens to have the same behavior. Why? Because the purpose of this problem is to understand how the intexToPostFix function (and, in particular, its depth argument) work.

   Use comments to explain the commands in the translated program. Here is an example of commenting the PostFix code that was generated by translating the Intex program example (intex 4 (* (- ($ 1) ($ 2)) (/ ($ 3) ($ 4)))) in Lec 31 (see slide 4 of the Lec 31 Intex solution slides).

   (postfix 4 1 nget ; $1
              3 nget ; $2, know that $1 on stack
              sub ; (- $1 $2) 
              4 nget ; $3, know that (- $1 $2) on stack
              6 nget ; $4, know that $3 and (- $1 $2) on stack
              div ; (/ $3 $4)
              mul ; (* (- $1 $2) (/ $3 $4))

4. (8 points) Consider running P_Intex on the four arguments [4, 9, 8, 2]. In your AST for P_Intex from part a, annotate each expression node with the list of integers that corresponds to the PostFix stack that will be encountered just before the last command translated for that node by expToCmds is executed in the PostFix program P_PostFix. As shown above, you should write the stack as an SML-style list to the right of the node below the depth.

   For example, below is the result of annotating the Intex AST for (intex 4 (* (- ($ 1) ($ 2)) (/ ($ 3) ($ 4)))) with depth information and the stack before executing each node when the program is given the arguments [15, 8, 30, 5].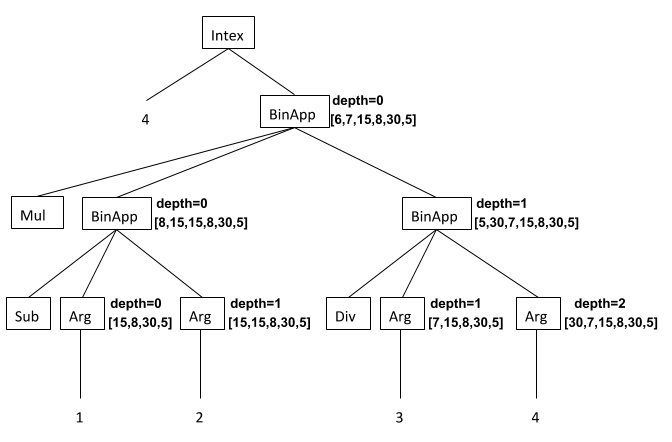

   

   Some things to observe:

   • At each Arg node in the program, the PostFix stack index of that argument in the stack annotating the node is the Arg index value plus the depth annotating the node. In particular:
     • The Arg node with index 1 has depth 0, and so translates to 1 nget.
     • The Arg node with index 2 has depth 1, and so translates to 3 nget.
     • The Arg node with index 3 has depth 1, and so translates to 4 nget.
     • The Arg node with index 4 has depth 2, and so translates to 6 nget.
   • Only Intex expression nodes (BinApp and Arg nodes in this example) have annotations. The binop nodes Sub, Div, and Mul are not annotated, nor are the Arg index values or the top-level Intex program node.
   • Here's an explanation of the stack annotations on the Intex AST nodes in the example:
     1. Execution of the translated program begins with the translation of the Arg node with index 1 to 1 nget. Before these commands are executed, the stack just contains the four argument values: [15, 8, 30, 5]. The result of executing the PostFix code for this node is [15, 15, 8, 30, 5]. The fact that the value of the left operand of Sub has been pushed on the stack causes the depth to increment from 0 to 1 for the right operand.
     2. The translated program executes the translation of the Arg node with index 2, which is 3 nget. Before these commands are executed, the stack contains the result of executing the PostFix code in Step 1, so the stack is [15, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [8, 15, 15, 8, 30, 5].
     3. The translated program performs the sub command translated for the end of the code for the Sub BinApp node. Before the subtraction is performed, the stack is the result of executing the PostFix code in Step 2, so the stack is [8, 15, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [7, 15, 8, 30, 5]. Since two stack values were popped but one was pushed when executing sub. So the depth for the next step (the division BinApp) is still 1.
     4. The translated program executes the translation of the Arg node with index 3, which is 4 nget. Before these commands are executed, the stack contains the result of executing the PostFix code in Step 3, so the stack is [7, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [30, 7, 15, 8, 30, 5]. Pushing the left operand of the Div BinApp increments the depth from 1 to 2 for its right operand.
     5. The translated program executes the translation of the Arg node with index 4, which is 6 nget. Before these commands are executed, the stack contains the result of executing the PostFix code in Step 4, so the stack is [30, 7, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [5, 30, 7, 15, 8, 30, 5].
     6. The translated program performs the div command translated for the end of the code for the Div BinApp node. Before the divistion is performed, the stack is the result of executing the PostFix code in Step 5, so the stack is [5, 30, 7, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [6, 7, 15, 8, 30, 5].
     7. The translated program performs the mul command translated for the end of the code for the Mul BinApp node. Before the multiplication is performed, the stack is the result of executing the PostFix code in Step 6, so the stack is [6, 7, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [42, 15, 8, 30, 5]. This stack is not shown in the annotated tree, but is the final stack for the program (which returns the result value 42).

</ul>

Problem 5. Extending Intex with a Conditional Expression (32 points)

Starting this Problem

This problem involves files in the ~/cs251/sml/ps6 directory in your csenv Virtual Machine.

To create this directory, execute this Linux commands in a shell on your csenv appliance:

cd ~/cs251/sml
git pull origin master

If you encounter any issues when executing these commands, you can troubleshoot by following these git instructions. If these instructions don’t help, please contact Lyn.

Begin this problem by renaming 2 files::

• Rename the starter file Condex.sml in ~/cs251/sml/ps6 to yourAccountName-Condex.sml.

• Rename the starter file CondexToPostFix.sml in ~/cs251/sml/ps6 to yourAccountName-CondexToPostFix.sml.

• In your renamed file yourAccountName-CondexToPostFix.sml, edit this line near the top of the file

  use "Condex.sml"; (* semi-colon required! *)

  to be

  use "yourAccountName-Condex.sml"; (* semi-colon required! *)

It is important to rename these files at the very beginning, because renaming the files protects you from git issues if I need to modify the starter files.

REMINDER: ALWAYS MAKE A BACKUP OF YOUR .sml FILES AT THE END OF EACH DAY TO AVOID POTENTIAL LOSS OF WORK.

The Condex Language

Both tasks in this problem involve the Condex language, which is an extension to Intex. As in Intex, all values in Condex are integers. But Condex includes the follow extra features:

1. Condex includes the relational operators <, =, and >. Since all Condex values are integers, these operators return 1 in the true case and 0 in the false case. This is similar to relational operators in PostFix.

2. Condex includes the conditional expression (ifnz E_test E_then E_else) where ifnz stands for if-non-zero and is pronounced iffenz. The meaning of the ifnz expression is as follows:

   First, the E_test expression is evaluated to an integer value V_test.

   • If V_test is non-zero, then the E_then expression is evaluated, and its value is returned as the value of the ifnz expression;

   • If V_test is zero, then the E_else expression is evaluated, and its value is returned as the value of the ifnz expression;

   • If an error is encountered during any of these evaluations, evaluating the ifnz expression gives the same error.

   As with Racket’s if expresssion, Condex’s ifnz evaluates at most two subexpressions. E_test is always evaluated, and if that evaluation does not give an error, exactly one of E_then or E_else is evaluated.

Condex programs are like Intex programs, except they begin with the symbol condex rather than intex. Your ~/cs251/sml/ps6 directory contains several sample Condex programs (with extension .cdx) that we will now discuss:

• The program in the file abs.cdx calculates the absolute value of its single argument:

  (condex 1 (ifnz (< $1 0) (- 0 $1) $1))

• The program simpleIf.cdx uses ifnz in a simple conditional test:

  (condex 2 (ifnz (< $1 $2) (+ $1 $2) (* $1 $2)))

  For example, running this program on the arguments 3 and 4 should return 7, but calling it on 4 and 3 should return 12.

• The program min3.cdx returns the smallest of its three arguments:

  (condex 3 (ifnz (< $1 $2)
                  (ifnz (< $1 $3) $1 $3)
                  (ifnz (< $2 $3) $2 $3)))

  For example, running this program on three arguments 4, 5, and 6 (in any order) should return 4.

• The program sumRelations.cdx doesn’t contain any occurrences of ifnz, but uses the fact that relational operations return 0 or 1 to sum the value of three such operations:

  (condex 4 (+ (< $1 $2) (+ (= $1 $3) (> $1 $4))))

  For example, running this program on the four arguments 5, 6, 5, 4 returns 3, because (< 5 6), (= 5 5), and (> 5 4) all return 1. But running it on the four arguments 5, 3, 7, 4 returns 1, because (< 5 3) and (= 5 7) return 0 and only (> 5 4) returns 1.

• In a Lec 30 Jamboard exercise, we considered translating the following Racket function to PostFix because it illustrated the importance of evaluating only one of the then and else branches (since the branch that’s not supposed to be taken could encounter and error).

  (define (test a b c)
    (if (> a b) (/ b c) (remainder b a)))

  The lec30Test.cdx program below is how the above Racket program would be expressed in Condex:

  (condex 3 (ifnz (> $1 $2) (/ $2 $3) (% $2 $1)))

  Using the examples from Lec 30:

  • running this program on the arguments 0, -8, and 2 should return -4 from the then branch (but not execute the else branch expression (% -8 0), which would encounter a remainder-by-zero error).

  • running this program on the arguments 5, 8, and 0 should return 3 from the else branch (but not execute the then branch expression (/ 8 0), which would encounter a divide-by-zero error).

  However, running it on the arguments 2, 1, 0 would encounter a divide-by-zero error in the then branch, and the arguments 0, 1, 2 would enounter a remainder-by-zero error in the else branch.

  This lec30Test.cdx program will be a particularly relevant example when we consider compiling Condex to PostFix in Part b of this problem.

• Problem 3a of this PS6, considers another Racket function, g, for translation into PostFix

  (define (g a b c)
    (- c
       (if (= 0 (remainder a 2))
           (quotient b (- a c))
           (* (+ b c) a))))

  The Condex program prob3a-g.cdx expresses this function in Condex:

  (condex 3 (- $3 (ifnz (= 0 (% $1 2))
                        (/ $2 (- $1 $3))
                        (* (+ $2 $3) $1))))

  Some relevant test cases from Problem 3a are that the three arguments 10, 2, and 8 yield the result 7, and the argments 5, 3, 5 yield the result -40. (See the comments in the file for more test cases.

• As a final example, the nestedIfs.cdx program is a complex program that uses ifnz expressions as the test, then, and else subexpressions of an outer ifnz expression.

  (condex 3 (ifnz (ifnz (< $1 $2) (< $1 $3) (> $1 $3))
            (ifnz (= $2 $3) (* $2 $2) (% $2 $3))
            (ifnz (> $2 $3) (/ $2 $3) (- $3 $2))))

  See the comments of this file for several test cases.