PS5: Resistance is Futile. You Will Be SMLated.
 )
)
- Dueish: Fri Dec 04
- It is not expected that you will work on this pset during Thanksgiving break. It will be OK if you don’t look at this pset until Mon. Nov. 30.
- However, this pset is being provided before Thanksgiving break for students who may wish to make some progress on it over break in order to reduce their workload after break.
- It is strongly recommened that you find a PS5 partner ASAP. Use this Pset Partners Doc to find a partner. It’s very important to make sure your partner has the same expectations as you regarding whether or not you plan to do any work on the pset over break, so when signing up in the Doc, indicate your expectations in this regard.
- Notes:
- This pset has 105 total points.
- The first problem involves reading parts of a long paper. It is best to spread this problem out over multiple sittings, and discuss the paper with your partner (if you have one). It is recommended that you work on this paper reading problem in parallel with the SML programming problems. a
- The second problem on 2-3-Trees involves the manipulation of a nontrivial tree data structure. It is based on the Lec 22 material on sum-of-product datatypes.
- The third and fourth problems involve different implementations of structures (modules) implementing
the
SETsignature. This involves material on SML structures and signatures covered in Lec 24 (on Mon. Nov 30, after break). It is possible to make progress on these problems before Lec 24, but you may want to wait to start these problems after Lec 24. (I might post some asynchronous videos for Lec 24 before the end of break, and will make an announcement if I do so.)
-
Times from previous semesters:
Times Problem 1 Problem 2 Problem 3 Problem 4 Total average time (hours) 2.7 3.5 2.3 3.1 11.6 median time (hours) 2.4 3.0 2.0 3.0 10.4 25% took more than 3.4 4.0 2.9 3.9 14.2 10% took more than 4.0 5.0 3.3 5.0 17.3 -
How to Start PS5
-
Follow the instructions in the GDoc CS251-F20-T2 Pset Submission Instructions for creating your PS5 Google Doc. Put all written answers and a copy of all code into this PS5 GDoc. If you are working with a partner, only one of you needs to create this document, but you should link it from both of your List Docs.
-
For Problems 2, 3, and 4, you will need to execute the following in a shell in your
csenvappliance to get the~/cs251/sml/ps5directory that contains starter code for these problems:cd ~/cs251/sml git pull origin master
-
- Submission:
- For all parts of all problems, include all answers (code, English explanations, etc.) in your PS5 google doc. Please format your SML code using a fixed-width font, like Consolas or Courier New, and format it so that it’s easy to read. You can use a small font size if that helps.
- For Problem 1 (Backus paper): Include English answers to parts a through f, the Racket/SML code for part g, and the algebraic derivation from part h in your Google Doc.
- For part g, you do not need to submit the Racket/SML code to your drop folder.
- For Problems 2, 3, and 4, you will create the following code files from starter files populating your
~/cs251/sml/ps5directory on yourcsenvappliance:- Problem 2:
yourAccountName-TTTreeFuns.sml - Problem 3:
yourAccountName-FunSet.sml - Problem 4:
yourAccountName-OperationTreeSet.sml
For these problems: + include all functions from the three files named
yourAccountName...in your Google Doc (so that the graders can comment on them). + Drop a copy of your~/cs251/sml/ps5folder in your~/cs251/drop/ps05drop folder oncs.wellesley.eduby executing the following in yourcsenv appliance(replacing both occurrences ofgdomeby your cs server username):~~~ scp -r ~/cs251/sml/ps5 gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps05 ~~~ - Problem 2:
Guarding Against Data Loss: Taking Snapshots and Backing up your Work
This section still needs to be fleshed out.
1. Backus to the Future (25 points)
This problem involves the paper from John Backus’s 1977 Turing Award Lecture: Can Programming be Liberated from the von Neumann Style? A Functional Style and its Algebra of Programs. Backus led development of the procedural Fortran language in the 1950s. This lecture/paper demonstrates some shifts in thinking in the intervening 20 years.
We study this paper for two reasons:
-
It is a classic paper that clearly describes the benefits of a computational model based on functions and composition that stands in contrast to the imperative models of computation that are still prevalent today. The fact that it is written by the architect of Fortran, the common ancestor of all imperative languages, underscores the importance of these ideas and gives the arguments a ``pay attention to this” weight from someone who should know.
-
It introduces Backus’s FP programming language. In your final solo assignment, you will implement an interpreter for a subset of this language, so it is helpful to start learning about it now.
You should begin this problem by reading Sections 1–11 and 15–16 of this paper. (Although Sections 12–14 are very interesting, they require more time than I want you to spend on this problem.)
Section 11.2 introduces the details of the FP language. Backus uses many notations that may be unfamiliar to you. For example:
-
p1 → e1; … ; pn → en; en+1 is similar to the Racket expression
(ifp1e1…(ifpnenen+1)…). -
⟨e1, …, en⟩ denotes the sequence of the n values of the expressions e1, … en. φ denotes the empty sequence. Because FP is dynamically typed, such sequences can represent both tuples and lists from Python and SML.
-
The symbol ⊥ (pronounced “bottom”) denotes the value of an expression that doesn’t terminate (i.e., it loops infinitely) or terminates with an error.
-
If f is a function and x is an object (atom or sequence of objects), then f : x denotes the result of applying f to x.
-
[f1, …, fn] is a functional form denoting a sequence of n functions, f1 through fn. The application rule for this functional form is [f1, …, fn] : x = ⟨f1 : x, … , fn : x⟩ — i.e., the result of applying a sequence of n functions to an object x is an n-element sequence consisting of the results of applying each of the functions in the function sequence to x.
Consult Lyn if you have trouble understanding Backus’s notation.
Answer the following questions about Backus’s paper. Your answers should be concise but informative.
-
(2 points) One of the reasons this paper is well-known is that in it Backus coined the term “von Neumann bottleneck”. Describe what this is and its relevance to the paper.
-
(2 points) Many programming languages have at least two syntactic categories: expressions and statements. Backus claims that expressions are good but statements are bad. Explain his claim.
-
(3 points) In Sections 6, 7, and 9 of the paper, Backus discusses three problems/defects with von Neumann languages. Summarize them.
-
(3 points) What are applicative languages and how do they address the three problems/defects mentioned by Backus for von Neumann languages?
-
(1 points) The FP language Backus introduces in Section 11 does not support abstraction expressions like Racket’s
lambda. Why did Backus make this decision in FP? -
(2 points) Backus wrote this paper long before the development of Java and Python. Based on his paper, how do you think he would evaluate these two languages?
-
(2 points) Describe how the form [f1, …, fn] : x relates to the familiar
mapoperation from Racket and SML by writing an equivalent Racket or SML call tomap, assuming the function sequence, [f1, …, fn] is available as a list of functions bound to the variablefsand the valuexis is bound to the variablex. -
(10 points) Consider the following FP definition:
Def F ≡ α/+ ◦ αα× ◦ αdistl ◦ distr ◦ [id, id]What is the value of F⟨2, 3, 5⟩? Show the evaluation of this expression in a sequence of small-step algebra-like steps.
2. 2-3 Trees (30 points)
In this problem you will use SML to implement aspects of 2-3 trees, a particular search tree data structure that is guaranteed to be balanced.
Begin by skimming pages 1 through 7 of this handout on 2-3 trees. (I created this handout for CS230 in Fall, 2004, but 2-3 trees are no longer taught in that course).
In a 2-3 tree, there are three kinds of nodes: leaves, 2-nodes, and 3-nodes. Together, these can be expressed in SML as follows:
datatype TTTree = (* 2-3 tree of ints *)
L (* Leaf *)
| W of TTTree * int * TTTree (* tWo node *)
| H of TTTree * int * TTTree * int * TTTree (* tHree node *)For simplicity, we will only consider 2-3 trees of integers, though they can be generalized to handle any type of value.
For conciseness in constructing and displaying large trees, the three constructors have single-letter names. For example, below are the pictures of four sample 2-3 trees from the handout and how they would be expressed with these constructors:
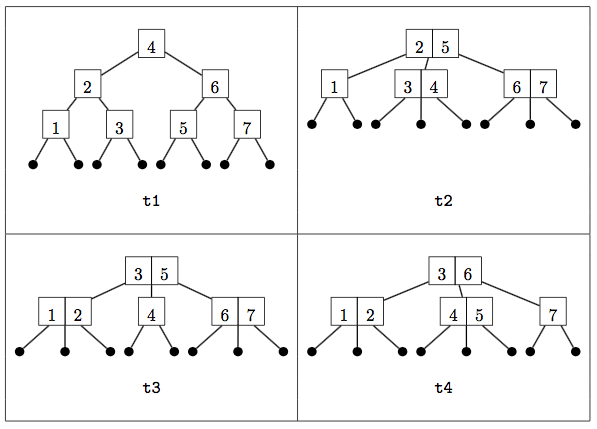
val t1 = W( W(W(L,1,L), 2, W(L,3,L)), 4, W(W(L,5,L), 6, W(L,7,L)))
val t2 = H( W(L,1,L), 2, H(L,3,L,4,L), 5, H(L,6,L,7,L))
val t3 = H( H(L,1,L,2,L), 3, W(L,4,L), 5, H(L,6,L,7,L))
val t4 = H( H(L,1,L,2,L), 3, H(L,4,L,5,L), 6, W(L,7,L))As explained in the handout on 2-3 trees, a 2-3 tree is only valid it it satisfies two additional properties:
- The ordering property:
- In a 2-node with left subtree l, value X, and right subtree r, (all values in l) ≤ X ≤ (all values in r).
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, (all values in l) ≤ X ≤ (all values in m) ≤ Y ≤ (all values in r).
- The height property (called path length invariant in the handout): in a 2-node or 3-node, the height of all subtrees must be exactly the same.
The height property guarantees that a valid 2-3 tree is balanced. Together, these two properties guarantee that a 2-3 tree is efficiently searchable.
Starter files for the SML problems for PS5 are included in the ~/cs251/sml/ps5 directory in your csenv appliance. Be sure to execute the following in a shell in your csenv appliance to get this ~/cs251/sml/ps5 folder:
cd ~/cs251/sml
git pull origin masterYour ~/cs251/sml/ps5 folder includes the file TTTree.sml, which contains the TTTree dataytype defined above as well as numerous examples of valid and invalid 2-3 trees that are instances of this datatype. Note that t and vt are used for valid trees, io is used for invalidly ordered trees, and ih is used for invalid height trees.
| tree name | elements | ordered? | satisfies the height property? |
|---|---|---|---|
| t1 | [1,…,7] | Yes | Yes, with height 3 |
| t2 | [1,…,7] | Yes | Yes, with height 2 |
| t3 | [1,…,7] | Yes | Yes, with height 2 |
| t4 | [1,…,7] | Yes | Yes, with height 2 |
| vt0 | [] | Yes | Yes, with height 0 |
| vt2 | [1,2] | Yes | Yes, with height 1 |
| vt17 | [1,…,17] | Yes | Yes, with height 3 |
| vt20 | [1,…,20] | Yes | Yes, with height 4 |
| vt44 | [1,…,44] | Yes | Yes, with height 5 |
| vt92 | [1,…,92] | Yes | Yes, with height 6 |
| io2 | [1,2] | No | Yes, with height 1 |
| io7 | [1,…,7] | No | Yes, with height 2 |
| io17 | [1,…,17] | No | Yes, with height 3 |
| io20 | [1,…,20] | No | Yes, with height 4 |
| io44 | [1,…,44] | No | Yes, with height 5 |
| io92 | [1,…,92] | No | Yes, with height 6 |
| ih2 | [1,2] | Yes | No |
| ih7 | [1,…,7] | Yes | No |
| ih17 | [1,…,17] | Yes | No |
| ih20 | [1,…,20] | Yes | No |
| ih44 | [1,…,44] | Yes | No |
| ih92 | [1,…,92] | Yes | No |
These trees are used to define two lists:
val validTrees = [vt0, vt2, t2, t3, t4, t1, vt17, vt20, vt44, vt92]
val invalidTrees = [io2, io7, io17, io20, io44, io92,
ih2, ih9, ih17, ih20, ih44, ih92]In this problem you will (1) implement a validity test for 2-3 trees and (2) implement the effcient 2-3 insertion algorithm from the handout on 2-3 trees.
Your ~/cs251/sml/ps5 folder also includes the starter file TTTreeFuns.sml. In this file, flesh out the missing definitions as specified below. When you finish this problem, rename the file to yourAccountName-TTTreeFuns.sml before you submit it.
-
satisfiesOrderingProperty(7 points)In this part, you will implement a function
satisfiesOrderingProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree ordering property andfalseif it does not. An easy way to do this is to define two helper functions:elts: TTTree -> int listreturns a list of all the elements of the tree in in-order — i.e.,- In a 2-node with left subtree l, value X, and right subtree r, all values in l are listed before X, which is listed before all elements in r.
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, all values in l are listed before X, which is listed before all values in m, which are listed before Y , which is listed before all values in r.
isSorted: int list -> boolreturnstrueif the list of integers is in sorted order andfalseotherwise.
For example:
- elts vt17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] : int list - elts io17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,17,16] : int list - isSorted(elts vt17); val it = true : bool - isSorted(elts io17); val it = false : boolUsing these two helper functions,
satisfiesOrderingPropertycan be implemented as:fun satisfiesOrderingProperty t = isSorted(elts t)For example:
- map satisfiesOrderingProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesOrderingProperty invalidTrees; val it = [false,false,false,false,false,false,true,true,true,true,true,true] : bool listNotes:
-
It is assumed that you are already familiar with running SML in Emacs from PS4 Problem 4.
-
(These workflow instructions have been simpflified on the evening of Dec 02, 2020) Your workflow on this problem should be as follows:
-
Open the file
TTTreeFuns.smland edit some definitions. -
Every time you change the file
TTTreeFuns.smland want to test your changes in the SML interpreter, load this file into the SML interpreter using one of the following two approaches. (Note: This file is configured to also automatically load the fileTTree.sml, which loads theTTTreedatatype and example trees.)-
If you’re running SML in Emacs in a
csenvappliance (strongly recommended), you can loadTTTreeFuns.smlvia these steps:</span>-
Open
~/cs251/sml/ps5/TTTreeFuns.smlin Emacs: use theC-x C-fkeyboard shortcut or the menu itemFile>Open File)</span> -
Load
TTTreeFuns.smlfile into a*sml*interpreter buffer: use theC-c C-bkeyboard shortcut (followed by areturnif prompted in the mini-buffer at the bottom of the screen) or the menu itemSML>Process>Send Buffer. You may need to scroll down in the*sml*buffer to see what has been loaded.
-
-
Otherwise (i.e., if you are running SML on tempest), in an SML interpreter, do the following:
- Posix.FileSys.chdir "/students/yourCSAccountName/cs251/sml/ps5"; val it = () : unit - use "TTTreeFuns.sml"; ... lots of printout omitted ...
-
-
-
You may need to execute
Control.Print.printLength := 100;in order to see all the list elements. -
Implement
isSortedusing the same zipping approach you used in PS3 Problem 4d. As seen in PS4 Problem 4b, you do zipping in SML viaListPair.zipfrom the ListPair module.List.allfrom the List module is also helpful.
-
satisfiesHeightProperty(9 points)In this part, you will implement a function
satisfiesHeightProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree height property andfalseif it does not. An easy way to do this is to definesatisfiesHeightPropertyasfun satisfiesHeightProperty t = Option.isSome (height t)where
Option.isSomeis a function from the Option module that determines if anoptionvalue is aSOME(vs. aNONE) andheightis a function with typeTTTree -> option intsuch thatheight treturnsSOME hiftsatisfies the height property with heighthand otherwise returnsNONE.Implement the
heightfunction by fleshing out this skeleton:(* height: TTTree -> int option *) fun height L = (* return an appropriate option value here *) | height (W(l, _, r)) = (case (height(l), height(r)) of (* put appropriate pattern clauses here *)) | (* handle the H case here, similarly to the W case *)For example:
- map height validTrees; val it = [SOME 0,SOME 1,SOME 2,SOME 2,SOME 2,SOME 3,SOME 3,SOME 4,SOME 5,SOME 6] : int option list - map height invalidTrees; val it = [SOME 1,SOME 2,SOME 3,SOME 4,SOME 5,SOME 6,NONE,NONE,NONE,NONE,NONE,NONE] : int option listNotes:
-
It’s important to enclose the
caseexpressions withinheightin parens to distinguish the pattern clauses of thecaseexpression from those of theheightfunction definition. -
You should not exhaustively match patterns for four combinations of
SOME/NONEfor a two-node and nine combinations for a three-node. Instead use the underscore pattern_to match “everything else”. With the underscore, only two patterns are necessary for handling two-nodes and two patterns are necessary for handling three-nodes. -
Once
heightis defined,satisfiesHeightPropertyis defined:- map satisfiesHeightProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesHeightProperty invalidTrees; val it = [true,true,true,true,true,true, false,false,false,false,false,false] : bool list -
Once both
satisfiesOrderingPropertyandsatisfiesHeightPropertyare defined, it is trivial to define a functionisValid: TTTree -> boolthat returnstrueif a given 2-3 tree is valid andfalseotherwise.fun isValid t = satisfiesOrderingProperty t andalso satisfiesHeightProperty t - map isValid validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map isValid invalidTrees; val it = [false,false,false,false,false,false, false,false,false,false,false,false] : bool list
-
-
insert(14 points) In this part, you will implement the insertion algorithm for 2-3 trees as described on pages 3 to 5 of the handout on 2-3 trees. You will not implement the special cases described on page 6 .The insertion algorithm is a recursive algorithm that uses the notion of a pseudo 2-node that is “kicked up” in certain cases and handled specially in the upward phase of the recursion. To distinguish an insertion result that is a regular 2-3 tree from a pseudo 2-node that is “kicked up”, we use the following datatype:
datatype InsResult = Tree of TTTree | KickedUp of TTTree * int * TTTree (* pseudo 2-node "kicked up" from below *)You will implement 2-3 tree insertion via a pair of functions:
-
(insert v t)returns the newTTTreethat results from inserting a given intvinto a given treet.inserthas typeint -> TTTree -> TTTree. -
(ins v t)is a helper function that returns the instance ofInsResultthat results from inserting a given intvinto a given treet.inshas typeint -> TTTree -> InsResult.
Your implementation should flesh out the following code skeleton by turning the pictures on pages 3 to 5 from the handout on 2-3 trees into SML code.
(* insert: int -> TTTree -> TTTree *) fun insert v t = case ins v t of Tree t => t | KickedUp(l, w, r) => W(l, w, r) and (* "and" glues together mutually recursive functions *) (* ins: int -> TTTree -> InsResult *) ins v L = KickedUp (L, v, L) | ins v (W(l, X, r)) = if v <= X then (case ins v l of Tree l' => Tree(W(l', X, r)) | KickedUp (l', w, m) => Tree(H(l', w, m, X, r))) else (* flesh this out *) | (* handle an H node similarly to the W node based on rules from the handout *)Notes:
-
The
insfunction should only callinsrecursively and should not callinsert. -
Students are often mishandling the
KickedUpcase for 3-nodes, which leads to type errors and/or testing errors. There are two common bugs with translating the pictorial rules on page 5 of the 2-3 Tree handout:-
When translating the pictures into SML code, it is not possible to keep all the same variable names as shown in the pictures. It is necessary to carefully rename some of these variables to be consistent with the pattern at the beginning of your
insfunction on a 3-node. -
If you carefully study the pictures for handling KickedUp nodes for 3-nodes you’ll see that each right-hand side returns a new
KickedUpnode and not aTree. If you incorrectly return aTree, you’ll get errors when testing.
-
-
An easy way to test
insertis to use thetestInsertfunction defined at the end of the starter file.fun listToTTTree xs = foldl (fn (x,t) => insert x t) L xs fun range lo hi = if lo >= hi then [] else lo :: (range (lo + 1) hi) fun testInsert numVals = let val inputs = range 0 numVals val ttt = listToTTTree inputs val _ = if isValid ttt then print "Tree is valid.\n" else print "***TEST FAILED: Tree is invalid!\n" val _ = if elts ttt = inputs then print "Tree contains all inputs in expected order.\n" else print "***TEST FAILED: Tree elements are not what is expected!\n" in ttt endGiven a nonnegative integer n,
testInsertcreates a 2-3 tree by inserting the integers from 0 up to (but not including) n in an initially empty tree. It also checks that the resulting tree is valid and contains exactly the expected numbers.- testInsert 5; Tree is valid. Tree contains all inputs in expected order. val it = H (W (L,0,L),1,W (L,2,L),3,W (L,4,L)) : TTTree - testInsert 10; Tree is valid. Tree contains all inputs in expected order. val it = W (W (W #,1,W #),3,H (W #,5,W #,7,H #)) : TTTreeBy default, SML uses the
#character to hide tree details below a default depth of 5. You can set this depth to be higher as shown below:- Control.Print.printDepth := 100; val it = () : unit - testInsert 10; Tree is valid. Tree contains all inputs in expected order. val it = W (W (W (L,0,L),1,W (L,2,L)),3,H (W (L,4,L),5,W (L,6,L),7,H (L,8,L,9,L))) : TTTree - testInsert 50; Tree is valid. Tree contains all inputs in expected order. val it = H (W (W (W (W (L,0,L),1,W (L,2,L)),3,W (W (L,4,L),5,W (L,6,L))),7, W (W (W (L,8,L),9,W (L,10,L)),11,W (W (L,12,L),13,W (L,14,L)))),15, W (W (W (W (L,16,L),17,W (L,18,L)),19,W (W (L,20,L),21,W (L,22,L))),23, W (W (W (L,24,L),25,W (L,26,L)),27,W (W (L,28,L),29,W (L,30,L)))),31, W (W (W (W (L,32,L),33,W (L,34,L)),35,W (W (L,36,L),37,W (L,38,L))),39, W (W (W (L,40,L),41,W (L,42,L)),43, H (W (L,44,L),45,W (L,46,L),47,H (L,48,L,49,L))))) : TTTreetestInsertcan find some bugs in yourinsertfunction. Here’s an example where it reports a tree that is invalid because its left subtree has height 1 while its right subtree has height 2:- testInsert 5; ***TEST FAILED: Tree is invalid! Tree contains all inputs in expected order. val it = W (W (L,0,L),1,W (W (L,2,L),3,W (L,4,L))) : TTTree -
Unfortunately, inserting elements in sequential order as above tends to create 2-3 trees with almost all 2-nodes and very few 3-nodes, so it can easily miss bugs in your insertion cases that involve 3-nodes.
It turns out a better way to test
insertis to insert integers in a range that have been “shuffled” in various ways, which gives a better distribution of 2-nodes and 3-nodes, and is more likely to catch bugs in yourinsertfunction. This approach to testing is implemented in the separate fileTTTreeFunsTest.sml, which will test yourinsertfunction on thousands of test cases.Before using the file
TTTreeFunsTest.sml, open it in an editor and change the lineuse "TTTreeFuns.sml"; (* Student solutions *)to
use "yourAccountName-TTTreeFuns.sml"; (* Student solutions *)Then send the contents of this modified file to
*sml*` buffer. If you do this, the final values will look like the following when yourinsertfunction passes all the test cases::val testInsertUpToSize5 = ("Passed all 8 test cases",[]) : string * (int list * TTTree) list val testInsertUpToSize10 = ("Passed all 28 test cases",[]) : string * (int list * TTTree) list val testInsertUpToSize25 = ("Passed all 172 test cases",[]) : string * (int list * TTTree) list val testInsertUpToSize50 = ("Passed all 613 test cases",[]) : string * (int list * TTTree) list val testInsertUpToSize100 = ("Passed all 2152 test cases",[]) : string * (int list * TTTree) list val it = () : unitIf there are test cases that fail, a list of up to 10 input/output cases where the output tree is incorrect will be shown. For example:
val testInsertUpToSize5 = ("FAILED TEST CASES: invalid trees in these input/output pairs", [([0,1,2,3,4],W (W (L,0,L),1,W (W (L,2,L),3,W (L,4,L)))), ([0,1,3,2,4],W (W (L,0,L),1,W (W (L,2,L),3,W (L,4,L))))]) : string * (int list * TTTree) list
-
3. Fun Sets (20 points)
In SML, we can implement abstract data types in terms of familiar structures like lists and trees. But we can also use functions to implement data types. In this problem, you will investigate a compelling example of using functions to implement sets.
Your ~/cs251/sml/ps5 folder contains the starter file FunSet.sml. This includes the same SET signature we studied in class:
signature SET =
sig
(* The type of sets *)
type ''a t
(* An empty set *)
val empty : ''a t
(* Construct a single-element set from that element. *)
val singleton : ''a -> ''a t
(* Check if a set is empty. *)
val isEmpty : ''a t -> bool
(* Return the number of elements in the set. *)
val size : ''a t -> int
(* Check if a given element is a member of the given set. *)
val member : ''a -> ''a t -> bool
(* Construct a set containing the given element and all elements
of the given set. *)
val insert : ''a -> ''a t -> ''a t
(* Construct a set containing all elements of the given set
except for the given element. *)
val delete : ''a -> ''a t -> ''a t
(* Construct the union of two sets. *)
val union : ''a t -> ''a t -> ''a t
(* Construct the intersection of two sets. *)
val intersection : ''a t -> ''a t -> ''a t
(* Construct the difference of two sets
(all elements in the first set but not in the second.) *)
val difference : ''a t -> ''a t -> ''a t
(* Construct a set from a list of elements.
Do not assume the list elements are unique. *)
val fromList : ''a list -> ''a t
(* Convert a set to a list without duplicates.
The elements in the resulting list may be in any order. *)
val toList : ''a t -> ''a list
(* Construct a set from a predicate function:
the resulting set should contain all elements for which
this predicate function returns true.
This acts like math notation for sets. For example:
{ x | x mod 3 = 0 }
would be written:
fromPred (fn x => x mod 3 = 0)
*)
val fromPred : (''a -> bool) -> ''a t
(* Convert a set to a predicate function. *)
val toPred : ''a t -> ''a -> bool
(* Convert a set to a string representation, given a function
that converts a set element into a string representation. *)
val toString : (''a -> string) -> ''a t -> string
(* Convert a set to a list without duplicates.
The elements in the resulting list may be in any order. *)
val toList : ''a t -> ''a list
(* Construct a set from a predicate function:
the resulting set should contain all elements for which
this predicate function returns true.
This acts like math notation for sets. For example:
{ x | x mod 3 = 0 }
would be written:
fromPred (fn x => x mod 3 = 0)
*)
val fromPred : (''a -> bool) -> ''a t
(* Convert a set to a predicate function. *)
val toPred : ''a t -> ''a -> bool
(* Convert a set to a string representation, given a function
that converts a set element into a string representation. *)
val toString : (''a -> string) -> ''a t -> string
endBelow is the initial contents of the starter file FunSet.sml:
exception Unimplemented (* Placeholder during development. *)
exception Unimplementable (* Impossible to implement *)
(* Implement a SET ADT using predicates to represent sets. *)
structure FunSet :> SET = struct
(* Sets are represented by predicates. *)
type ''a t = ''a -> bool
(* The empty set is a predicate that always returns false. *)
val empty = fn _ => false
(* The singleton set is a predicate that returns true for exactly one element *)
fun singleton x = fn y => x=y
(* Determining membership is trivial with a predicate *)
fun member x pred = pred x
(* complete this structure by replacing "raise Unimplemented"
with implementations of each function. Many of the functions
*cannot* be implemented; for those, use raise Unimplementable
as there implementation *)
fun isEmpty _ = raise Unimplemented
fun size _ = raise Unimplemented
fun member _ = raise Unimplemented
fun insert _ = raise Unimplemented
fun delete _ = raise Unimplemented
fun union _ = raise Unimplemented
fun intersection _ = raise Unimplemented
fun difference _ = raise Unimplemented
fun fromList _ = raise Unimplemented
fun toList _ = raise Unimplemented
fun fromPred _ = raise Unimplemented
fun toPred _ = raise Unimplemented
fun toString _ = raise Unimplemented
endThe most important aspect of this implementation is that sets are represented by predicates, i.e., functions that return a boolean:
(* Sets are represented by predicates. *)
type ''a t = ''a -> boolIn particular, if p is a predicate representing a set, the elements of that set are
all values v for which p v is true.
The fromPred and toPred operations are based on the observation that a membership predicate describes exactly which elements are in the set and which are not. Consider the following example:
- val s235 = fromPred (fn x => (x = 2) orelse (x = 3) orelse (x = 5));
val s235 = - : int t
- member 2 s235;
val it = true : bool
- member 3 s235;
val it = true : bool
- member 5 s235;
val it = true : bool
- member 4 s235;
val it = false : bool
- member 100 s235;
val it = false : boolThe set s235 consists of exactly those elements satisfying the predicate passed to fromPred – in this case, the integers 2, 3, and 5.
Defining sets in terms of predicates has many benefits. Most important, it is easy to specify sets that have infinite numbers of elements! For example, the set of all even integers can be expressed as:
fromPred (fn x => (x mod 2) = 0)This predicate is true of even integers, but is false for all other integers. The set of all values of a given type is expressed as fromPred (fn x => true). Many large finite sets are also easy to specify. For example, the set of all integers between 251 and 6821 (inclusive) can be expressed as
fromPred (fn x => (x >= 251) andalso (x <= 6821))Although defining sets in terms of membership predicates is elegant and has many benefits, it has some big downsides. The biggest one is that several functions in the SET signature simply cannot be implemented. You will explore this downside in this problem.
-
(16 points) Begin this problem by making a copy of
FunSet.smlyourAccountName-FunSet.sml. Make all your edits toyourAccountName-FunSetand not toFunSet.sml</span>.Flesh out the code skeleton for the
FunSetstructure inyourAccountName-FunSet.sml. Some value bindings cannot be implemented; for these, useraise Unimplementableas the implementation.Notes:
-
The notion that a set can be implemented as a predicate function is a mind-blowing example of the power of using functions to implement data structures!
-
In this set implementation, the only function in which list operations make sense is in
fromList. It is an error to use list operations elsewhere. -
Since a predicate is a function of one argument that returns a boolean, when returning a set-as-predicate, it is always sensible to use an expression of the form
fn y =>boolexp, where y is the candidate element being tested for membership, and boolexp is a boolean-valued expression indicating whetheryis in the set. -
Various tests of the
FunSetimplementation are performed in the separate fileFunSetTest.sml. In the fileFunSetTest.sml, change the lineuse "FunSet.sml";touse "yourAccountName-FunSet.sml";, and send its contents to the*sml*buffer, it will define atestResultsvalue that summarizes the results of 14 test cases as a list of strings. If it passes all 14 test cases, the next-to-last line will be:val testResults = ["Passed all 14 test cases:"] : string listIf some test cases fail, this will be indicated in the list of strings in the value of
testResults. For example:val testResults = ["------------------------------------------------------------", "Passed 13 test cases:","smallSet","smallerSet","mod2Set","mod3Set", "mod2SetIntersectionMod3Set","mod2SetDifferenceMod3Set", "mod3SetDifferenceMod2Set","mod3SetDifferenceMod2Set","lowSet","middleSet", "highSet","bigIntersection","bigDifference", "------------------------------------------------------------", "Failed 1 test case:","mod2SetUnionMod3Set:", "expected = [0,2,3,4,6,8,9,10,12,14,15,16,18,20,21,22,24,26,27,28,30,32,33,34,36,38,39,40,42,44,45,46,48,50,51,52,54,56,57,58\ ,60,62,63,64,66,68,69,70,72,74,75,76,78,80,81,82,84,86,87,88,90,92,93,94,96,98,99,100]", " actual = [0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96]", "------------------------------------------------------------"] : string list
-
-
(4 points) For each function that you declared being unimplementable, explain in English why it is unimplementable. Give concrete examples where appropriate.
4. Operation Tree Sets (30 points)
A very different way of representing a set as a tree is to use a sum-of-products data structure to remember the structure of the set operations empty, insert, delete, union, intersection, and difference used to create the set. For example, consider the set s created as follows:
val s = (delete 4 (difference (union (union (insert 1 empty)
(insert 4 empty))
(union (insert 7 empty)
(insert 4 empty)))
(intersection (insert 1 empty)
(union (insert 1 empty)
(insert 6 empty)))))Abstractly, s is the singleton set {7}. But one concrete representation of s is the following operation tree:

One advantage of using such operation trees to represent sets is that the empty, insert, delete, union, difference, and intersection operations are extremely cheap — they just create a new tree node with the operands as subtrees, and thus take constant time and space! But other operations, such as member and toList, are typically more expensive than in other implementations.
In this problem, you are asked to flesh out the missing operations in the skeleton of the OperationTreeSet structure shown below. Your ~/cs251/sml/ps5 folder contains the starter file OperationTreeSet.sml.
Begin this problem by making a copy of OperationTreeSet.sml named yourAccountName-OperationTreeSet.sml. Make all your edits to yourAccountName-OperationTreeSet.sml and not to OperationTreeSet.sml.
structure OperationTreeSet :> SET = struct
datatype ''a t = Empty
| Insert of ''a * ''a t
| Delete of ''a * ''a t
| Union of ''a t * ''a t
| Intersection of ''a t * ''a t
| Difference of ''a t * ''a t
val empty = Empty
fun insert x s = Insert(x,s)
fun singleton x = Insert(x, Empty)
fun delete x s = Delete(x, s)
fun union s1 s2 = Union(s1,s2)
fun intersection s1 s2 = Intersection(s1,s2)
fun difference s1 s2 = Difference(s1,s2)
fun member _ _ = raise Unimplemented
fun toList _ = raise Unimplemented
fun isEmpty _ = raise Unimplemented
fun size _ = raise Unimplemented
fun toPred _ = raise Unimplemented
fun toString eltToString _ = raise Unimplemented
fun fromList _ = raise Unimplemented
fun fromPred _ = raise Unimplementable
endIn the OperationTreeSet structure, the set datatype t is create by constructors Empty, Insert, Delete, Union, Intersection, and Difference. The empty, singleton, insert, delete, union, intersection, difference operations are easy and have been implemented for you. You are responsible for fleshing out the definitions of the member, toList, size, isEmpty, toPred, toString, and fromList operations.
Notes:
-
Only in the definitions of the
memberandtoListfunctions should you do a case analysis on the six kinds of node constructors. -
There are two ways to express the case analysis on the six node types in
member(and similarly fortoList) that are shown below. In both approaches, it is absolutely necessary to wrap all patterns exceptEmptyin parens.-
Approach 1:
fun member x s = (case s of Empty => ... | (Insert(y, s')) => ... use x, y, & s' here ... | (Delete(y, s')) => ... use x, y, & s' here ... | (Union(s1, s2)) => ... use x, s1 & s2 here ... | (Difference(s1, s2)) => ... use x, s1, & s2 here ... | (Intersection(s1, s2)) => ... use x, s1, & s2 here ... ) -
Approach 2:
fun member x Empty = ... | member x (Insert(y, s)) = ... use x, y, & s here ... | member x (Delete(y, s)) = ... use x, y, & s here ... | member x (Union(s1, s2)) = ... use x, s1 & s2 here ... | member x (Difference(s1, s2)) = ... use x, s1 & s2 here ... | member x (Intersection(s1, s2)) = ... use x, s1 & s2 here ...
-
-
Your implementation of
membershould not use thetoListfunction. Instead, it should be defined by case analysis on the structure of the operation tree. -
For the
toListfunction:-
toListshould also be defined by case analysis on the structure of the operation tree. -
The
memberfunction should not be used in the implementation oftoList(because it can be very inefficient). Instead, useList.existsandList.filterin a manner similar to the way we implemented sets as lists without duplicates in class. -
Keep in mind that sets are unordered. So your
toListfunction may return lists of elements in any order, but it should not have any duplicates. -
In your
toListdefinition, be very careful with includingtoListinside functional arguments, because this can often cause the same list to be calculated a tremendous number of times, leading to tests that take a very long time for large sets. If some of the test cases for large sets don’t return in a reasonable time, this is probably the cause. You can avoid this by using SML’slet/in/endto name the result of calculatingtoListand using the name multiple times.
-
-
Your implementations of
size,isEmpty, andtoStringshould use thetoListfunction. Indeed, it is difficult to implement these functions by a direct case analysis on the operation tree. Note thatsizewill only work correcty if the output oftoListdoes not contain duplicates. -
Your implementation of
toPredmay use either thememberfunction or thetoListfunction. -
The
toStringfunction should return comma-separated elements delimited by curly braces, as in “{5,2,3,4}”. -
In the implementation of
toString, the functionString.concatWithis particularly useful. -
In the implementation of
fromList, for lists with >= 2 elements, you should first split the list into two (nearly) equal-length sublists usingList.takeandList.dropand union the results of turning the sublists into sets. This yields a height-balanced operation tree. -
Various tests of the
OperationTreeSetimplementation are performed in the separate fileOperationTreeSetTest.sml. In the fileOperationTreeSetTest.sml, change the lineuse "OperationTreeSet.sml";touse "yourAccountName-OperationTreeSet.sml";, and send its contents to the*sml*buffer, it will (among other things) perform 216 tests that are organized by groups, and will print out information about each test. The very last line will be a summary. If you seePassed all 216 teststhen you needn’t dig deeper. But if you see a message like
***FAILED 20 tests; passed 196 teststhen you should scroll back through the printout to find the test case(s) that misbehaved. For example, you might see:
s1DifferenceS2: ***Failed! actual: [19,57,97] expected: [19] s2DifferenceS1: ***FAILED! actual: [19,57,97] expected: [57,97] intersectionSmallDiffs: ***FAILED! actual: [19,57,97] expected: [] smallDelete: passed!To understand why the
expectedresult was expected, you need to study the test cases inOperationTreeSetTest.sml. -
The testing code for most functions (all except for
member) assumes thattoListworks correctly. So you must implementtoListfor most of the tests to work. However, all the tests will run, and some of them may even succeed, even if many of the functions haveraise Unimplementedas their implementations. -
If running
OperationTreeSetTest.smlappears to get ``stuck”, especially when testing the group bigLists, it is most likely due to an issue mentioned above fortoList. That is, usingtoListinside functional arguments can easily make thetoListfunction take exponential time and be very slow.
Extra Credit 1: 2-3 Tree Deletion (20 points)
In SML, implement and test the 2-3 tree deletion algorithm presented in pages 8 through 11 of the handout on 2-3 trees. You will need to develop test cases that show that your implementation works as expected.
Extra Credit 2: 2-3 Trees in Java (40 points)
-
(25 points) Implement and test 2-3 tree insertion in Java, using test cases similar to the ones used in SML in Problem 2. Also include a brief discussion of which features of which languages make the implementation easier and why?
-
(15 points) Implement and test 2-3 tree deletion in Java.