CS 251: Solo Assignment D

Dueish: Thu Dec 03. But working with a partner on PS5 has a higher priority than this solo assignment.
Notes:
- This is a solo assignment. You must complete all parts of this assignment entirely on your own without help from any other person and without consulting any resources other than course materials or Racket documentation. You may ask Lyn for clarification, but not for help.
- You can do all problems on this assignment based on material you learned for PS4. Be sure to study the solutions to PS4 before doing this assignment.
- This assignment has two solo problems worth 40 solo points.
How to Start Solo Assignment D

Follow the instructions in the GDoc CS251-F20-T2 Pset Submission Instructions for creating your SOLO-D Google Doc. Put all written answers and a copy of all code into this SOLO-D GDoc.
Submission:
- For all parts of all problems, include all answers (including box-and-pointer diagrams and all Racket & SML code) in your SOLO-D GDoc. Please format your Racket & SML function definitions so that they’re easy to read. Format all derivations and code using a fixed-width font (Courier New or Consolas). You use a small font size if that helps.
- For Problem 1 (Diagonal Duples):
  - Be sure that all function definitions in yourAccountName-solo-d-duples.rkt also also appear in your SOLO-D GDoc (so that I can comment on them)
  - Drop a copy of your yourAccountName-solo-d-duples.rkt in your ~/cs251/drop/solo-d drop folder on cs.wellesley.edu.
- For Problem 2 (Partial Reverses):
  - Include the box-and-pointer diagram from Part a in your SOLO-D GDoc;
  - Include the answer to Part b in your SOLO-D GDoc;
  - Include the SML functions definitions for Parts c, d, e in your SOLO-D GDoc (so that I can comment on them);
  - Drop a copy of your ~/cs251/sml/solo-d/yourAccountName-partialReverses.sml file in your ~/cs251/drop/solo-d drop folder on cs.wellesley.edu by executing the following in your csenv appliance (replacing all three occurrences of gdome by your cs server username):
```
scp -p ~/cs251/sml/solo-d/gdome-partialReverses.sml gdome@cs.wellesley.edu:/students/gdome/cs251/drop/solo-d
```

1. Diagonal Duples (22 points)

Begin this problem by downloading this starter file solo-d-duples.rkt, which you should rename to yourAccountName-solo-d-duples.rkt. This file contains provided definitions for this solo problem.

This problem concerns one of the provided functions in yourAccountName-solo-d-duples.rkt.

(define (diagonal-duples n) ; Assume is n a nonnegative integer
  (foldr append null
         (map (λ (sum)
                (map (λ (fst) (list fst (- sum fst)))
                     (range 0 (+ sum 1))))
              (range 0 (+ n 1)))))

(3 points) The diagonal-duples function generates a list of duples (2-element lists) of integers related to input n, in a very particular order. Carefully describe in English the output list of duples in terms of n. As in PS4 Problem 3a, do not describe the Racket code or algorithm that generates the duples. Instead, specify (1) exactly what duples are in the output list (in a general way, not giving examples) and (2) exactly what order the duples are in. Your description must be precise enough that someone else could implement the diagonal-duples function correctly based on your description, without seeing the original Racket definition. (You should carefully study the PS4 Problem 3a solution before answering this part.)

(5 points) Recall the genlist-apply function from lecture and PS4 (which is supplied as a helper function in yourAccountName-solo-d-duples.rkt).

(define (genlist-apply next done? keepDoneValue? seed)
  (if (apply done? seed)
      (if keepDoneValue? (list seed) null)
      (cons seed
            (genlist-apply next done? keepDoneValue? (apply next seed)))))

In the file yourAccountName-solo-d-duples.rkt, define a Racket function diagonal-duples-genlist-apply that has the same input/output behavior as diagonal-duples but is defined using genlist-apply by fleshing out the missing expressions denoted by the quoted symbols in the following skeleton:

(define (diagonal-duples-genlist-apply n) ; Assume is n a nonnegative integer
  (genlist-apply 'next-function-goes-here
                 'done-function-goes-here
                 'keep-done-value-goes-here
                 'seed-goes-here
                 ))

Note: Carefully study the solution to pairs-genlist-apply from PS4 Problem 3c before beginning this part.

(6 points) Recall the iterate-apply function from lecture and PS4 (which is supplied as a helper function in yourAccountName-solo-d-duples.rkt):
```
(define (iterate-apply next done? finalize state)
  (if (apply done? state)
      (apply finalize state)
      (iterate-apply next done? finalize (apply next state))))
```
In the file yourAccountName-solo-d-duples.rkt, define a Racket function diagonal-duples-iterate-apply that has the same input/output behavior as diagonal-duples but is defined using iterate-apply by fleshing out the missing expressions denoted by the quoted symbols in the following skeleton:
```
(define (diagonal-duples-iterate-apply n) ; Assume is n a nonnegative integer
  (iterate-apply 'next-function-goes-here
                 'done?-function-goes-here
                 'finalize-function-goes-here
                 'initial-state-goes-here
                 ))
```
Notes:
- Carefully study the solution to pairs-iterate-apply from PS4 Problem 3d before beginning this part.
- Unlike the diagonal-duples-genlist-apply function, which add duples from the front of the list to the end, your diagonal-duples-iterate-apply implementation should add duples from the end of the list to the beginning.
- In this function you should not use snoc, append, or reverse on any lists. You should only use cons to extend a list. Why? Because repeated snocing leads to quadratic running times. How? By constructing the desired output list in reverse, starting with the last duple and working your way back to the first duple.
- As in PS4 Problem 3d, it may be helpful to use iteration tables involving concrete examples to help you define this function.
(8 points) In the file yourAccountName-solo-d-duples.rkt, define a tail-recursive Racket function diagonal-duples-iter that has the same input/output behavior as diagonal-duples but is defined iteratively using tail-recursive helper functions.

For full credit, your definition should flesh out this exact skeleton with nested function definitions:
```
(define (diagonal-duples-iter n) ; Assume is n a nonnegative integer
  (define (outer-tail {outer-parameters})
    (define (inner-tail {inner-parameters})
      {inner-body}) ; call inner_tail and outer-tail tail-recursively in inner-body
    {outer-body) ; call inner_tail tail-recursively in outer-body
  (outer-tail ...)
```
Substantial partial credit can be earned for other iterative solutions that use tail recursion, such as solutions that use a single tail-recursive helper function.

Notes:
- Carefully study the solution to pairs-iter-nested from PS4 Problem 3f before beginning this part.
- Unlike the diagonal-duples-genlist-apply function, which add duples from the front of the list to the end, your diagonal-duples-iter implementation should add duples from the end of the list to the beginning (like you did in diagonal-duples-iterate-apply).
- For the same reasons as in diagonal-duples-iterate-apply, in this function you should not use snoc, append, or reverse on any lists.
- IMPORTANT: Just naming a function to end in -tail does not make it tail recursive! In order to be tail recursive, all calls of your tail recursive functions must not be subexpressions of other function calls. E.g. in the code
```
(if <test>
    <then> 
    (outer-tail (inner-tail ...) ...))
```
  the call to outer-tail is a tail call, but the the call to inner-tail is not a tail call (because it is a subexpression of another call).

2. Partial Reverses (18 points)

Begin this problem via these two steps:

Execute the following in a shell in your csenv appliance to get the ~/cs251/sml/solo-d directory that contains SML starter code for Parts c, d, and e of this problem:</span>
```
cd ~/cs251/sml
git pull origin master
```
Make a copy of partialReverses.sml named yourAccountName-partialReverses.sml. You will write your code answers for Parts c, d, and e of this problem in yourAccountName-partialReverses.sml

(5 points) Consider the following partial-reverses function in Racket. Draw a box-and-pointer diagram of the list that results from the invocation (partial-reverses '(1 2 3 4)). Use the style of diagram shown in PS2 Problem 2. Study the code carefully and be sure to accurately show all sharing between cons cells in your diagram.
```
(define (partial-reverses xs)
  (define (partial-reverses-tail ys rev list-rev)
    (if (null? ys)
        (cons rev list-rev)
        (partial-reverses-tail (rest ys)
                               (cons (first ys) rev)
                               (cons rev list-rev)
                               )))
  (partial-reverses-tail xs '() '()))
```
Note: As an example of sharing in box-and-pointer diagrams, consider
```
(define numList '(7 2 4))

(define listOfNumLists (list (append numList (rest numList)) numList (rest numList)))
```
The result has 9 cons cells arranged as follows:

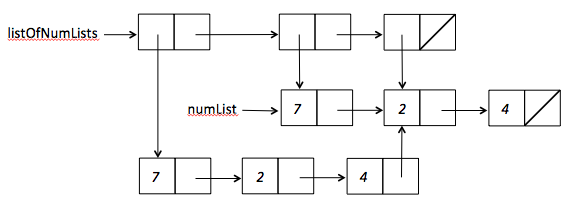
However, if we just enter the printed representation '((7 2 4 2 4) (7 2 4) (2 4)) for listOfNumLists, that would create 13 cons cells (because in this case there would be no sharing of cons cells):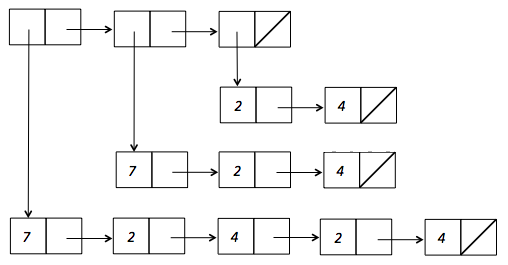
(2 points) How many cons cells would there be in the result of (partial-reverses (range 1 1001))?
(5 points) In yourAccountName-partialReverses.sml, translate the Racket definition of partial-reverses into an SML function partialReverses that has exactly the same behavior (in terms of generating lists with the same sharing).

Similar to the partial-reverses function in Racket, the SML partialReverses function should have a nested function definition partialReversesTail that is called within it.

As in PS4 Problem 4, in this and the following parts of this solo problem, do not use #1, #2, etc. to extract tuple components or List.hd, List.tl, or List.null to decompose and test lists. Instead, use pattern matching on tuples and lists.
(4 points) In yourAccountName-partialReverses.sml, flesh out the following SML skeleton definition of partialReversesIterate so that it uses iterate to iteratively calculate the same result (including sharing) as partialReverses:
```
fun partialReversesIterate xs = 
  iterate (* expression1 *)
          (* expression2 *)
          (* expression3 *)
          (xs, [], [])
```
yourAccountName-partialReverses.sml includes this definition of iterate (from PS4 Problem 4b):
```
(* val iterate = fn : ('a -> 'a) -> ('a -> bool) -> ('a -> 'b) -> 'a -> 'b *)
fun iterate next isDone finalize state =
  if isDone state then
      finalize state
  else
      iterate next isDone finalize (next state)
```
Notes:
- In yourAccountName-partialReverses.sml, the definition of iterate must appear above the defintion of partialReversesIterate, which uses it.
- You are allowed use List.null or = [] or to test for an empty list in this part only.
(2 Points) In yourAccountName-partialReverses.sml, flesh out the following skeleton definition of partialReversesFoldl so that it uses foldl to iteratively calculate the same result (including sharing) as partialReverses:
```
fun partialReversesFoldl xs = 
   foldl (* expression1 *)
         (* expression2 *)          
         xs
```
Recall that SML’s foldl function has type ('a * 'b -> 'b) -> 'b -> 'a list -> 'b.