PS8: Set Yourself Free
- Dueish: Fri. Dec. 01, 2017
- Notes:
- This pset has 105 total points.
- This pset contains one solo problems worth 20 points.
- It is strongly recommended that you do the non-solo SML problems (Problems 3 and 4) first, to get more practice with SML and modules/abstract datatypes that will be valuable going forward.
- Submission:
- In your yourFullName CS251 Spring 2017 Folder, create a Google Doc named yourFullName CS251 PS8.
- At the top of your yourFullName CS251 PS8 doc, include your name, problem set number, date of submission, and an approximation of how long each problem part took.
- For all parts of all problems, include all answers (including SML and Racket code) in your PS8 google doc. Format code using a fixed-width font, like Consolas or Courier New. You can use a small font size if that helps.
- For Problems 2, include your interpretation/compilation derivations. It is easiest to write these via nested bullets, as shown in both the pset description and the lecture notes.
- In Problems 1, 3, and 4, you will create the following code files from starter files populating your
~wx/cs251/sml/ps8directory on your wx Virtual Machine:- Problem 1:
yourAccountName-marbles.sml - Problem 3:
yourAccountName-FunSet.sml - Problem 4:
yourAccountName-OperationTreeSet.sml
For these problems:
- include all functions from the four files named
yourAccountName...in your Google Doc (so that I can comment on them). - For Problem 3b, don’t forget to include your English answers in your Google Doc.
-
Drop a copy of your
~wx/cs251/sml/ps8folder in your~/cs251/drop/ps08drop folder oncs.wellesley.eduby executing the following (replacinggdomeby your cs server username):scp -r ~wx/cs251/sml/ps8 gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps08
- Problem 1:
Starting this Problem Set
Problems 1, 3, and 4 involve starter files in the ~wx/cs251/sml/ps8 directory in your wx Virtual Machine.
To create this directory, execute the following four commands in a wx terminal shell:
cd ~/cs251/sml
git add -A
git commit -m "my local changes"
git pull origin master --rebaseSeveral students have encountered problems when executing this steps. If you have problems, please contact lyn.
1. Solo Problem: Losing Your Marbles (20 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
Put all your definitions for this problem in the starter file ~/cs251/sml/ps8/marbles.sml. When you finish this problem, rename the file to yourAccountName-ps8-marbles.sml before you submit it.
In this problem, you will define an SML function satisfying the following specification:
val marbles: int -> int -> int list list
Assume that
mis a non-negative integer and thatcis a positive integer. Givenmmarbles and a row ofccups,marbles m creturns a sorted list of all configurations whereby allmmarbles are distributed among theccups. Each configuration should be a list of lengthcwhose elements are integers between 0 andmand the sum of whose elements ism. The returned list should be ordered lexicographically (i.e., in dictionary order).
At the end of this problem description are numerous sample invocations of the marbles function.
Your task is to define the marbles function in SML so that it satisfies the above specification and has the same behavior as the sample invocations below.
(* Execute the following to display elements beyond the default cutoff length for lists *)
- Control.Print.printLength := 100;
val it = () : unit
- marbles 0 1;
val it = [[0]] : int list list
- marbles 0 2;
val it = [[0,0]] : int list list
- marbles 0 3;
val it = [[0,0,0]] : int list list
- marbles 0 4;
val it = [[0,0,0,0]] : int list list
- marbles 1 1;
val it = [[1]] : int list list
- marbles 1 2;
val it = [[0,1],[1,0]] : int list list
- marbles 1 3;
val it = [[0,0,1],[0,1,0],[1,0,0]] : int list list
- marbles 1 4;
val it = [[0,0,0,1],[0,0,1,0],[0,1,0,0],[1,0,0,0]] : int list list
- marbles 2 1;
val it = [[2]] : int list list
- marbles 2 2;
val it = [[0,2],[1,1],[2,0]] : int list list
- marbles 2 3;
val it = [[0,0,2],[0,1,1],[0,2,0],[1,0,1],[1,1,0],[2,0,0]] : int list list
- marbles 2 4;
val it =
[[0,0,0,2],[0,0,1,1],[0,0,2,0],[0,1,0,1],[0,1,1,0],[0,2,0,0],[1,0,0,1],
[1,0,1,0],[1,1,0,0],[2,0,0,0]] : int list list
- marbles 3 1;
val it = [[3]] : int list list
- marbles 3 2;
val it = [[0,3],[1,2],[2,1],[3,0]] : int list list
- marbles 3 3;
val it =
[[0,0,3],[0,1,2],[0,2,1],[0,3,0],[1,0,2],[1,1,1],[1,2,0],[2,0,1],[2,1,0],
[3,0,0]] : int list list
- marbles 3 4;
val it =
[[0,0,0,3],[0,0,1,2],[0,0,2,1],[0,0,3,0],[0,1,0,2],[0,1,1,1],[0,1,2,0],
[0,2,0,1],[0,2,1,0],[0,3,0,0],[1,0,0,2],[1,0,1,1],[1,0,2,0],[1,1,0,1],
[1,1,1,0],[1,2,0,0],[2,0,0,1],[2,0,1,0],[2,1,0,0],[3,0,0,0]]
: int list list
- marbles 4 1;
val it = [[4]] : int list list
- marbles 4 2;
val it = [[0,4],[1,3],[2,2],[3,1],[4,0]] : int list list
- marbles 4 3;
val it =
[[0,0,4],[0,1,3],[0,2,2],[0,3,1],[0,4,0],[1,0,3],[1,1,2],[1,2,1],[1,3,0],
[2,0,2],[2,1,1],[2,2,0],[3,0,1],[3,1,0],[4,0,0]] : int list list
- marbles 4 4;
val it =
[[0,0,0,4],[0,0,1,3],[0,0,2,2],[0,0,3,1],[0,0,4,0],[0,1,0,3],[0,1,1,2],
[0,1,2,1],[0,1,3,0],[0,2,0,2],[0,2,1,1],[0,2,2,0],[0,3,0,1],[0,3,1,0],
[0,4,0,0],[1,0,0,3],[1,0,1,2],[1,0,2,1],[1,0,3,0],[1,1,0,2],[1,1,1,1],
[1,1,2,0],[1,2,0,1],[1,2,1,0],[1,3,0,0],[2,0,0,2],[2,0,1,1],[2,0,2,0],
[2,1,0,1],[2,1,1,0],[2,2,0,0],[3,0,0,1],[3,0,1,0],[3,1,0,0],[4,0,0,0]]
: int list list
- marbles 5 1;
val it = [[5]] : int list list
- marbles 5 2;
val it = [[0,5],[1,4],[2,3],[3,2],[4,1],[5,0]] : int list list
- marbles 5 3;
val it =
[[0,0,5],[0,1,4],[0,2,3],[0,3,2],[0,4,1],[0,5,0],[1,0,4],[1,1,3],[1,2,2],
[1,3,1],[1,4,0],[2,0,3],[2,1,2],[2,2,1],[2,3,0],[3,0,2],[3,1,1],[3,2,0],
[4,0,1],[4,1,0],[5,0,0]] : int list list
- marbles 5 4;
val it =
[[0,0,0,5],[0,0,1,4],[0,0,2,3],[0,0,3,2],[0,0,4,1],[0,0,5,0],[0,1,0,4],
[0,1,1,3],[0,1,2,2],[0,1,3,1],[0,1,4,0],[0,2,0,3],[0,2,1,2],[0,2,2,1],
[0,2,3,0],[0,3,0,2],[0,3,1,1],[0,3,2,0],[0,4,0,1],[0,4,1,0],[0,5,0,0],
[1,0,0,4],[1,0,1,3],[1,0,2,2],[1,0,3,1],[1,0,4,0],[1,1,0,3],[1,1,1,2],
[1,1,2,1],[1,1,3,0],[1,2,0,2],[1,2,1,1],[1,2,2,0],[1,3,0,1],[1,3,1,0],
[1,4,0,0],[2,0,0,3],[2,0,1,2],[2,0,2,1],[2,0,3,0],[2,1,0,2],[2,1,1,1],
[2,1,2,0],[2,2,0,1],[2,2,1,0],[2,3,0,0],[3,0,0,2],[3,0,1,1],[3,0,2,0],
[3,1,0,1],[3,1,1,0],[3,2,0,0],[4,0,0,1],[4,0,1,0],[4,1,0,0],[5,0,0,0]]
: int list listNotes:
-
As usual, you should use divide/conquer/glue as your problem-solving strategy. Don’t attemot to write any code until you understand your strategy.
-
Don’t forget the very powerful notion of “wishful” thinking, in which you blindly apply a recursive function to smaller versions of the same problem and combine their results. Study the examples carefully to see how the result of a call to
marblesis stitched together from the results of calls to “smaller” versions ofmarbles. -
Strive to make your solution as simple as possible. For example, do not use more base cases than are strictly necessary.
-
Your
marblesfunction should generate the elements in sorted order without calling any kind of sorting function. -
You are expected to use higher-order list functions where they can simplify your definition.
-
The stater file begins with the following helper functions, which you might find useful:
fun cons x ys = x :: ys (* curried list consing operator *) fun range lo hi = (* list all ints from lo up to (but not including) hi *) List.tabulate(hi - lo, fn i => i + lo)Reminder: these and other helper functions must be defined above your definition of
marbles, because definition order matters in SML. -
Feel free to define any additional auxiliary functions you find helpful.
2. Metaprogramming Derivations (35 points)
2a. Deriving Implementations (18 points)
As we discussed in the Metaprogramming lecture, there are two basic reasoning rules involving interpreters, translators (a.k.a. compilers), and program implementation:
The Interpreter Rule (I)
The Translator Rule (T)
In practice, we often elide the word “machine” for interpreter machines and translator machines. For example, we will refer to an “L interpreter machine” as an “L interpreter”, and an “S-to-T translator machine” as an “S-to-T translator” or “S-to-T compiler”. We will also often elide the word “program”; e.g., we will refer to a “P-in-L program” as “P-in-L”. So an “L interpreter” means an “L interpreter machine” while a “S-in-L interpreter” means an “S-in-L interpreter program”. Similar remarks hold for translators (also called compilers): an “S-to-T translator” means an “S-to-T translator machine”, while a “S-to-T-in-L translator” means an “S-to-T-in-L translator program”.
Example
For example, we considered the following elements in class:
- a 251-web-page-in-HTML program (i.e., a 251 web page written in HTML)
- an HTML-interpreter-in-C program (i.e., a web browser written in C)
- a C-to-x86-compiler-in-x86 program (i.e., a C-to-x86 compiler written in x86)
- a x86 computer (i.e., an x86 interpreter machine)
They can be used to build a 251 web page display machine as follows:
Feel free to abbreviate by dropping the words “program” and “machine”. “… in …” denotes a program, while “… compiler” and “… translator” denote translator machines and “… interpreter” and “… computer” denote interpreter machines.
Writing Derivations
Rather that displaying derivations using horizontal lines, it is recommended that you use nested bullets to indicate the same structure as the inference rules (though drawn “upside down”). For example, the derivation above could also be written:
- 251 web page machine (I)
- 251-web-page-in-HTML program
- HTML interpreter machine (I)
- HTML-interpreter-in-x86 program (T)
- HTML-interpreter-in-C program
- C-to-x86 compiler machine (I)
- C-to-x86-compiler-in-x86 program
- x86 computer
- x86 computer
- HTML-interpreter-in-x86 program (T)
Questions
i. (9 points) Suppose you are given the following:
- A P-in-Java program
- a Java-to-C-compiler-in-Racket program (i.e., a Java-to-C compiler written in Racket);
- a Racket-interpreter-in-x86 program (i.e., a Racket interpreter written in x86 machine code);
- a C-to-x86-compiler-in-x86 program (i.e., a C-to-x86 compiler written in x86 code);
- an x86 computer (i.e., an x86 interpreter machine).
Using the two reasoning rules above, construct a “proof” that demonstrates how to execute the P-in-Java program on the computer. That is, show how to construct a P machine.
ii. (9 points) Suppose you are given:
- a GraphViz-in-C program
- a C-to-LLVM-compiler-in-x86 program
- an LLVM-to-JavaScript-compiler-in-x86 program
- a JavaScript-interpreter-in-ARM program
- an x86 computer (i.e., an x86 interpreter machine, such as your laptop)
- an ARM computer (i.e., an ARM interpreter machine, such as a smartphone)
Show how to construct a GraphViz machine.
Notes:
-
In the above two parts, it is not possible to derive a “C interpreter”, a “Java interpreter”, or an “LLVM interpreter”, so if you need or use such a part in your derivation, you’ve done something wrong.
-
As shown in the above examples, you should use an (I) or (T) to indicate a conclusion that results from the Interpreter or Translator rule, respectively. Double check that the conclusion is actually justified by the rule from two nested bullets below the conclusion.
2b. Bootstrapping (17 points)
In his Turing Award lecture-turned-short-paper Reflections on Trusting Trust, Ken Thompson describes how a compiler can harbor a so-called “Trojan horse” that can make compiled programs insecure. Read this paper carefully and do the following tasks to demonstrate your understanding of the paper:
i. (7 points) Stage II of the paper describes how a C compiler can be “taught” to recognize '\v' as the vertical tab character. Using the same kinds of components and processes used in Problem 1, we can summarize the content of Stage II by carefully listing the components involved and describing (by constructing a proof) how a C compiler that “understands” the code in Figure 2.2 can be generated. (Note that the labels for Figures 2.1 and 2.2 are accidentally swapped in the paper.) In Stage II, two languages are considered:
- the usual C programming language
- C+\v = an extension to C in which
'\v'is treated as the vertical tab character (which has ASCII value 11).
Suppose we are given the following:
- a C-to-binary compiler (Here, “binary” is the machine code for some machine. This compiler is just a “black box”; we don’t care where it comes from);
- a C+\v-to-binary-compiler-in-C (Figure 2.3 in Thompson’s paper);
- a C+\v-to-binary-compiler-in-C+\v (what should be Figure 2.2 in Thompson’s paper);
- a machine that executes the given type of binary code.
Construct a proof showing how to use the C+\v-to-binary-compiler-in-C+\v source code to create a C+\v-to-binary-compiler-in-binary program.
ii. (10 points) Stage III of the paper describes how to generate a compiler binary harboring a “Trojan horse”. Using the same kinds of components and processes used in Problem 1, we can summarize the content of Stage III by carefully listing the components involved and describing (by constructing a proof) how the Trojaned compiler can be generated. In particular, assume we have the parts for this stage:
- a C-to-binary-compiler (again, just a “black box” we are given);
- a C-to-binary-compiler-in-C without Trojan Horses (Figure 3.1 in Thompson’s paper);
- a C-to-binary-compilerTH-in-C with two Trojan Horses (Figure 3.3 in Thompson’s paper);
- a login-in-C program with no Trojan Horse;
- a binary-based computer;
The subscript TH indicates that a program contains a Trojan Horse. A C-to-binary compilerTH has the “feature” that it can insert Trojan Horses when compiling source code that is an untrojaned login program or an untrojaned compiler program. That is, if P is a login or compiler program, it is as if there is a new rule:
The Trojan Horse Rule (TH)
Using these parts along with the two usual rules (I) and (T) and the new rule (TH), show how to derive a Trojaned login program loginTH-in-binary that is the result of compiling login-in-C with a C compiler that is the result of compiling C-to-binary-compiler-in-C. The interesting thing about this derivation is that loginTH-in-binary contains a Trojan horse even though it is compiled using a C compiler whose source code (C-to-binary-compiler-in-C) contains no code for inserting Trojan horses!
Notes:
-
Although only 3 pages long, the Thompson paper is very dense and challenging. Don’t be surprised if it requires multiple readings to ``get’’ the ideas, which are profound.
-
Double-check your derivations to make sure that they make sense and actually describe what’s being said in Thompson’s paper.
3. Fun Sets (22 points)
In SML, we can implement abstract data types in terms of familiar structures like lists and trees. But we can also use functions to implement data types. In this problem, you will investigate a compelling example of using functions to implement sets.
Your ~wx/cs251/sml/ps8 folder contains the starter file FunSet.sml. This includes the same SET signature we studied in class:
signature SET =
sig
(* The type of sets *)
type ''a t
(* An empty set *)
val empty : ''a t
(* Construct a single-element set from that element. *)
val singleton : ''a -> ''a t
(* Check if a set is empty. *)
val isEmpty : ''a t -> bool
(* Return the number of elements in the set. *)
val size : ''a t -> int
(* Check if a given element is a member of the given set. *)
val member : ''a -> ''a t -> bool
(* Construct a set containing the given element and all elements
of the given set. *)
val insert : ''a -> ''a t -> ''a t
(* Construct a set containing all elements of the given set
except for the given element. *)
val delete : ''a -> ''a t -> ''a t
(* Construct the union of two sets. *)
val union : ''a t -> ''a t -> ''a t
(* Construct the intersection of two sets. *)
val intersection : ''a t -> ''a t -> ''a t
(* Construct the difference of two sets
(all elements in the first set but not in the second.) *)
val difference : ''a t -> ''a t -> ''a t
(* Construct a set from a list of elements.
Do not assume the list elements are unique. *)
val fromList : ''a list -> ''a t
(* Convert a set to a list without duplicates.
The elements in the resulting list may be in any order. *)
val toList : ''a t -> ''a list
(* Construct a set from a predicate function:
the resulting set should contain all elements for which
this predicate function returns true.
This acts like math notation for sets. For example:
{ x | x mod 3 = 0 }
would be written:
fromPred (fn x => x mod 3 = 0)
*)
val fromPred : (''a -> bool) -> ''a t
(* Convert a set to a predicate function. *)
val toPred : ''a t -> ''a -> bool
(* Convert a set to a string representation, given a function
that converts a set element into a string representation. *)
val toString : (''a -> string) -> ''a t -> string
(* Convert a set to a list without duplicates.
The elements in the resulting list may be in any order. *)
val toList : ''a t -> ''a list
(* Construct a set from a predicate function:
the resulting set should contain all elements for which
this predicate function returns true.
This acts like math notation for sets. For example:
{ x | x mod 3 = 0 }
would be written:
fromPred (fn x => x mod 3 = 0)
*)
val fromPred : (''a -> bool) -> ''a t
(* Convert a set to a predicate function. *)
val toPred : ''a t -> ''a -> bool
(* Convert a set to a string representation, given a function
that converts a set element into a string representation. *)
val toString : (''a -> string) -> ''a t -> string
endIn this problem, you will flesh out the skeleton of the FunSet structure below. When you finish this probelm, you should rename this file to yourAccountName-FunSet.sml before you submit it.
exception Unimplemented (* Placeholder during development. *)
exception Unimplementable (* Impossible to implement *)
(* Implement a SET ADT using predicates to represent sets. *)
structure FunSet :> SET = struct
(* Sets are represented by predicates. *)
type ''a t = ''a -> bool
(* The empty set is a predicate that always returns false. *)
val empty = fn _ => false
(* The singleton set is a predicate that returns true for exactly one element *)
fun singleton x = fn y => x=y
(* Determining membership is trivial with a predicate *)
fun member x pred = pred x
(* complete this structure by replacing "raise Unimplemented"
with implementations of each function. Many of the functions
*cannot* be implemented; for those, use raise Unimplementable
as there implementation *)
fun isEmpty _ = raise Unimplemented
fun size _ = raise Unimplemented
fun member _ = raise Unimplemented
fun insert _ = raise Unimplemented
fun delete _ = raise Unimplemented
fun union _ = raise Unimplemented
fun intersection _ = raise Unimplemented
fun difference _ = raise Unimplemented
fun fromList _ = raise Unimplemented
fun toList _ = raise Unimplemented
fun fromPred _ = raise Unimplemented
fun toPred _ = raise Unimplemented
fun toString _ = raise Unimplemented
endThe fromPred and toPred operations are based on the observation that a membership predicate describes exactly which elements are in the set and which are not. Consider the following example:
- val s235 = fromPred (fn x => (x = 2) orelse (x = 3) orelse (x = 5));
val s235 = - : int t
- member 2 s235;
val it = true : bool
- member 3 s235;
val it = true : bool
- member 5 s235;
val it = true : bool
- member 4 s235;
val it = false : bool
- member 100 s235;
val it = false : boolThe set s235 consists of exactly those elements satisfying the predicate passed to fromPred – in this case, the integers 2, 3, and 5.
Defining sets in terms of predicates has many benefits. Most important, it is easy to specify sets that have infinite numbers of elements! For example, the set of all even integers can be expressed as:
fromPred (fn x => (x mod 2) = 0)This predicate is true of even integers, but is false for all other integers. The set of all values of a given type is expressed as fromPred (fn x => true). Many large finite sets are also easy to specify. For example, the set of all integers between 251 and 6821 (inclusive) can be expressed as
fromPred (fn x => (x >= 251) && (x <= 6821))Although defining sets in terms of membership predicates is elegant and has many benefits, it has some big downsides. The biggest one is that several functions in the SET signature simply cannot be implemented. You will explore this downside in this problem.
-
(18 points) Flesh out the code skeleton for the
FunSetstructure inFunSet.sml. Some value bindings cannot be implement; for these, useraise Unimplementableas the implementation.At the end of the starter file are the following commented out test cases. Uncomment these test cases to test your implementation. Feel free to add additional tests.
open FunSet (* range helper function *) fun range lo hi = if lo >= hi then [] else lo::(range (lo + 1) hi) (* Test an int pred set on numbers from 0 to 100, inclusive *) fun intPredSetToList predSet = List.filter (toPred predSet) (range 0 101) val mod2Set = fromPred (fn x => x mod 2 = 0) val mod3Set = fromPred (fn x => x mod 3 = 0) val lowSet = fromList (range 0 61) val highSet = fromList (range 40 101) val smallSet = insert 17 (insert 19 (insert 23 (singleton 42))) val smallerSet = delete 23 (delete 19 (delete 57 smallSet)) (* Be sure to print all details *) val _ = Control.Print.printLength := 101; val smallSetTest = intPredSetToList(smallSet) val smallerSetTest = intPredSetToList(smallerSet) val mod3SetTest = intPredSetToList(mod3Set) val mod2SetUnionMod3SetTest = intPredSetToList(union mod2Set mod3Set) val mod2SetIntersectionMod3SetTest = intPredSetToList(intersection mod2Set mod3Set) val mod2SetDifferenceMod3SetTest = intPredSetToList(difference mod2Set mod3Set) val mod3SetDifferenceMod2SetTest = intPredSetToList(difference mod3Set mod2Set) val bigIntersection = intPredSetToList(intersection (intersection lowSet highSet) (intersection mod2Set mod3Set)) val bigDifference = intPredSetToList(difference (difference lowSet highSet) (difference mod2Set mod3Set))For the test expressions generating lists, the results are as follows:
val smallSetTest = [17,19,23,42] : int list val smallerSetTest = [17,42] : int list val mod3SetTest = [0,3,6,9,12,15,18,21,24,27,30,33,36,39,42,45,48,51,54,57,60,63,66,69,72,75, 78,81,84,87,90,93,96,99] : int list val mod2SetUnionMod3SetTest = [0,2,3,4,6,8,9,10,12,14,15,16,18,20,21,22,24,26,27,28,30,32,33,34,36,38,39, 40,42,44,45,46,48,50,51,52,54,56,57,58,60,62,63,64,66,68,69,70,72,74,75,76, 78,80,81,82,84,86,87,88,90,92,93,94,96,98,99,100] : int list val mod2SetIntersectionMod3SetTest = [0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96] : int list val mod2SetDifferenceMod3SetTest = [2,4,8,10,14,16,20,22,26,28,32,34,38,40,44,46,50,52,56,58,62,64,68,70,74,76, 80,82,86,88,92,94,98,100] : int list val mod3SetDifferenceMod2SetTest = [3,9,15,21,27,33,39,45,51,57,63,69,75,81,87,93,99] : int list val bigIntersection = [42,48,54,60] : int list val bigDifference = [0,1,3,5,6,7,9,11,12,13,15,17,18,19,21,23,24,25,27,29,30,31,33,35,36,37,39] : int list -
(4 points) For each function that you declared being unimplementable, explain in English why it is unimplementable. Give concrete examples where appropriate.
4. Operation Tree Sets (28 points)
A very different way of representing a set as a tree is to remember the structure of the set operations empty, insert, delete, union, intersection, and difference used to create the set. For example, consider the set t created as follows:
val s = (delete 4 (difference (union (union (insert 1 empty)
(insert 4 empty))
(union (insert 7 empty)
(insert 4 empty)))
(intersection (insert 1 empty)
(union (insert 1 empty)
(insert 6 empty)))))Abstractly, s is the singleton set {7}. But one concrete representation of s is the following operation tree:
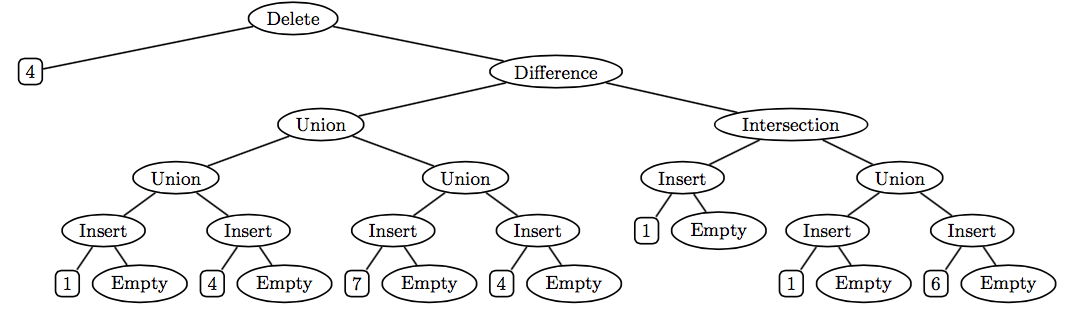
One advantage of using such operation trees to represent sets is that the empty, insert, delete, union, difference, and intersection operations are extremely cheap — they just create a new tree node with the operands as subtrees, and thus take constant time and space! But other operations, such as member and toList, can be more expensive than in other implementations.
In this problem, you are asked to flesh out the missing operations in the skeleton of the OperationTreeSet structure shown below. Your ~wx/cs251/sml/ps8 folder contains the starter file OperationTreeSet.sml. When you finish this problem, rename the file to yourAccountName-OperationTreeSet.sml before you submit it.
structure OperationTreeSet :> SET = struct
datatype ''a t = Empty
| Insert of ''a * ''a t
| Delete of ''a * ''a t
| Union of ''a t * ''a t
| Intersection of ''a t * ''a t
| Difference of ''a t * ''a t
val empty = Empty
fun insert x s = Insert(x,s)
fun singleton x = Insert(x, Empty)
fun delete x s = Delete(x, s)
fun union s1 s2 = Union(s1,s2)
fun intersection s1 s2 = Intersection(s1,s2)
fun difference s1 s2 = Difference(s1,s2)
fun member _ _ = raise Unimplemented
fun toList _ = raise Unimplemented
fun isEmpty _ = raise Unimplemented
fun size _ = raise Unimplemented
fun toPred _ = raise Unimplemented
fun toString eltToString _ = raise Unimplemented
fun fromList _ = raise Unimplemented
fun fromPred _ = raise Unimplementable
endIn the OperationTreeSet structure, the set datatype t is create by constructors Empty, Insert, Delete, Union, Intersection, and Difference. The empty, singleton, insert, delete, union, intersection, difference operations are easy and have been implemented for you. You are responsible for fleshing out the definitions of the member, toList, size, isEmpty, toPred, toString, and fromList operations.
Notes:
-
Your implementation of
membershould not use thetoListfunction. Instead, it should be defined by case analysis on the structure of the operation tree. -
Your
toListfunction should also be defined by case analysis on the structure of the operation tree. Thememberfunction should not be used in the implementation oftoList(because it can be very inefficient). Keep in mind that sets are unordered, and yourtoListfunction may return lists of elements in any order, but it should not have any duplicates. -
In your
toListdefinition, be very careful with includingtoListinside functional arguments, because this can often cause the same list to be calculated a tremendous number of times, leading to tests that take a very long time for large sets. If some of the test cases for large sets don’t return in a reasonable time, this is probably the cause. -
Your implementation of
sizeandisEmptyshould use thetoListfunction. Indeed, it is difficult to implement these functions by a direct case analysis on the operation tree. Note thatsizewill only work correcty if the output oftoListdoes not contain duplicates. -
In the implementation of
toString, the functionString.concatWithis particularly useful. -
In the implementation of
fromList, for lists with >= 2 elements, you should first split the list into two (nearly) equal-length sublists usingList.takeandList.dropand union the results of turning the sublists into sets. This yields a height-balanced operation tree. -
OperationTreeSet.smlends with two collections of test cases. The first collection involves “small” sets that are defined without usingfromList. The second collection involves “big” sets that are defined usingfromList. The expected outputs to these tests can be found in this transcript file. Because of the way the testing functions are written, the integer elements in the outputs formemberandtoPredwill be in sorted order from low to high, but the integers in the outputs fortoListandtoStringmay be in any order. -
The testing code for most functions (all except for
memberand assumes thattoListworks correctly. So you must implementtoListfor for most of the tests to work.
Extra Credit: Self-printing Program (15 points)
In his Turing-lecture-turned-short-paper Reflections on Trusting Trust, Ken Thompson notes that it is an interesting puzzle to write a program in a language whose effect is to print out a copy of the program. We will call this a self-printing program. Write a self-printing program in any general-purpose programming language you choose. Your program should be self-contained — it should not read anything from the file system.
Important Note: There are lots of answers on the Internet, but you will get zero points if you just copy one of those. (I can tell!) Do this completely one your own, without looking anything up online.