PS6: Resistance is Futile. You Will Be SMLated.
 )
)
- Dueish: Friday, Mar 24. Try to get as much of this pset done as you can before Spring break.
- Notes:
- This pset has 100 total points.
- This pset contains three solo problems worth 50 points. All solo problems use Racket, not SML.
- Do not attempt the solo problems until you have studied the solutions from PS4 and PS5.
- It is recommended that you do the SML problems before the Racket solo problems so that you can ask questions when you get stuck.
- Submission:
- In your yourFullName CS251 Spring 2017 Folder, create a Google Doc named yourFullName CS251 PS6.
- At the top of your yourFullName CS251 PS6 doc, include your name, problem set number, date of submission, and an approximation of how long each problem part took.
- For all parts of all problems, include all answers (including Racket and SML code) in your PS6 google doc. Format Racket and SML code using a fixed-width font, like Consolas or Courier New. You can use a small font size if that helps.
- For Problems 1, 2, 3 (the solo problems):
- Include the box-and-pointer diagram from 2a and your answers to 2b and 3a in your PS6 google doc.
- Be sure that the function definitions you wrote for these problems
yourAccountName-ps6-solo.rktalso appear in your Google Doc (so that I can comment on them) - Drop a copy of your
yourAccountName-ps6-solo.rktin your~/cs251/drop/ps06drop folder oncs.wellesley.edu.
- For Problems 4 and 5:
- Include the SML code from
yourAccountName-ps6-holo.smlin your Google Doc (so that I can comment on them). - Include the SML code from
yourAccountName-TTTreeFuns.smlin your Google Doc (so that I can comment on them). -
Drop a copy of your
~wx/cs251/sml/ps6folder in your~/cs251/drop/ps06drop folder oncs.wellesley.eduby executing the following (replacinggdomeby your cs server username):scp -r ~wx/cs251/sml/ps6 gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps06
- Include the SML code from
1. Solo Problem: It’s a Factor (16 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
Begin this problem by downloading this starter file ps6-solo-starter.rkt, which you should rename to yourAccountName-ps6-solo.rkt. This file contains provided definitions for Solo Problems 1, 2, and 3. Add your definitions for Problems 1, 2, and 3 to this file.
The following least-divisor-rec function correctly returns the least positive integer that evenly divides the given positive integer num.
(define (least-divisor-rec num) ;; Assume num is a postive integer
(let ((limit (ceiling (sqrt num)))) ;; The largest divisor to be tested
(define (search-for-divisor candidate)
(if (> candidate limit)
num
(if (divisible-by? num candidate)
candidate
(search-for-divisor (+ candidate 2)))))
(if (divisible-by? num 2)
2
(search-for-divisor 3))))
(define (divisible-by? num divisor)
(= (remainder num divisor) 0))We can use map with range to test least-divisor-rec on many inputs:
> (map (λ (n) (list n (least-divisor-rec n))) (range 45 56))
'((45 3) (46 2) (47 47) (48 2) (49 7) (50 2) (51 3) (52 2) (53 53) (54 2) (55 5))Using least-divisor-rec, we can define a function factors-rec that returns a list of all primes factors of a given positive integer, sorted from low to high:
(define (factors-rec num)
(let ((factor (least-divisor-rec num)))
(if (= factor num)
(list factor)
(cons factor (factors-rec (quotient num factor))))))
> (map (λ (n) (list n (factors-rec n))) (range 60 73))
'((60 (2 2 3 5))
(61 (61))
(62 (2 31))
(63 (3 3 7))
(64 (2 2 2 2 2 2))
(65 (5 13))
(66 (2 3 11))
(67 (67))
(68 (2 2 17))
(69 (3 23))
(70 (2 5 7))
(71 (71))
(72 (2 2 2 3 3)))-
(3 points) Using
factors-recin conjunction with the higher-orderforall?function defined in PS4 (it is one of your given helper functions), it is possible to give a very simple definition of thehamming?function from PS2. Flesh out this skeleton ofhamming?:(define (hamming? num) (and (integer? num) (> num 0) (or (= num 1) (forall? ; put expression 1 here ; put expression 2 here )) )) > (filter hamming? (range 0 101)) '(1 2 3 4 5 6 8 9 10 12 15 16 18 20 24 25 27 30 32 36 40 45 48 50 54 60 64 72 75 80 81 90 96 100)Recall that
forall?is defined as follows:(define (forall? pred xs) (if (null? xs) #t (and (pred (car xs)) (forall? pred (cdr xs))))) -
(4 points) Using the higher-order
findfunction defined in PS4 (it is one of your given helper functions), it is possible to define a functionleast-divisor-findthat searches through the same candidates to return the same answer asleast-divisor-recfor every positive integer input. Flesh out this skeleton ofleast-divisor-find:(define (least-divisor-find num) (find ; put expression 1 here ; put expression 2 here ; put expresion 3 here )) > (map (λ (n) (list n (least-divisor-find n))) (range 45 56)) '((45 3) (46 2) (47 47) (48 2) (49 7) (50 2) (51 3) (52 2) (53 53) (54 2) (55 5))Notes:
-
Recall that
findis defined as follows:(define (find pred not-found xs) (if (null? xs) not-found (if (pred (car xs)) (car xs) (find pred not-found (cdr xs))))) -
Your definition of
least-divisor-findshould should perform thedivisible-by?test on exactly the same candidates asleast-divisor-rec. -
For generating candidate divisors, it is helpful to know that the Racket
rangefunction (like the Pythonrangefunction) takes an optional thirdstepargument that is added to the current number to determine the next one. (The default step is 1.) For example:> (range 1 20 3) '(1 4 7 10 13 16 19) -
(least-divisor-find n)may take time proportional to the square root of n, even in cases whereleast-divisor-recwould return after a small number of steps (e.g., when n is an even number.) This is because it will create a list whose length is the square root of n even if it does not examine all the elements of that list. -
You are not allowed to use
factors-recin your definition ofleast-divisor-rec.
-
-
(4 points) Using the higher-order
genlistfunction we defined in class (it is one of your given helper functions), it is possible to define a functionfactors-genlistthat behaves likefactors-recfor every positive integer input. Flesh out the following skeleton offactors-genlist. You may useleast-divisor-recin your definition. [2017/05/04] This previously had only 3 expressions to be filled in, but really needs 4. The 3rd expression is forkeep-done-value?, which was missing in the previous version.(define (factors-genlist num) (map second (genlist ; put expression 1 here ; put expression 2 here ; put expression 3 here (list num ; put expression 4 here )))) > (map (λ (n) (list n (factors-genlist n))) (range 60 73)) '((60 (2 2 3 5)) (61 (61)) (62 (2 31)) (63 (3 3 7)) (64 (2 2 2 2 2 2)) (65 (5 13)) (66 (2 3 11)) (67 (67)) (68 (2 2 17)) (69 (3 23)) (70 (2 5 7)) (71 (71)) (72 (2 2 2 3 3)))Recall that genlist is defined as:
(define (genlist next done? keepDoneValue? seed) (if (done? seed) (if keepDoneValue? (list seed) null) (cons seed (genlist next done? keepDoneValue? (next seed))))) -
(5 points) Using the higher-order
iterate-applyfunction we defined in class (it is one of your given helper functions), it is possible to define a functionfactors-iterate-applythat behaves likefactors-recfor every positive integer input. Flesh out the following skeleton offactors-iterate-apply. You may useleast-divisor-recandreversein your definition.(define (factors-iterate-apply num) (iterate-apply ; put expression 1 here ; put expression 2 here ; put expression 3 here (list num null))) > (map (λ (n) (list n (factors-iterate-apply n))) (range 60 73)) '((60 (2 2 3 5)) (61 (61)) (62 (2 31)) (63 (3 3 7)) (64 (2 2 2 2 2 2)) (65 (5 13)) (66 (2 3 11)) (67 (67)) (68 (2 2 17)) (69 (3 23)) (70 (2 5 7)) (71 (71)) (72 (2 2 2 3 3)))Recall that
iterate-applyis defined as:(define (iterate-apply next done? finalize state) (if (apply done? state) (apply finalize state) (iterate-apply next done? finalize (apply next state))))
2. Solo Problem: Partial Reverses (17 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
In this problem, you will extend the yourAccountName-ps6-solo.rkt you created in Problem 1. This problem concerns one of the provided functions in that file:
-
(5 points) Consider the following
partial-reversesfunction. Draw a box-and-pointer diagram of the list that results from the invocation(partial-reverses '(1 2 3 4)). Use the style of diagram shown in PS3 Problem 2. Study the code carefully and be sure to accurately show all sharing between cons cells in your diagram.(define (partial-reverses xs) (partial-reverses-tail xs '() '())) (define (partial-reverses-tail ys rev list-rev) (if (null? ys) (cons rev list-rev) (partial-reverses-tail (rest ys) (cons (first ys) rev) (cons rev list-rev) )))Note: As an example of sharing in box-and-pointer diagrams, consider
(define numList '(7 2 4)) (define listOfNumLists (list (append numList (rest numList)) numList (rest numList)))The result has 9 cons cells arranged as follows:
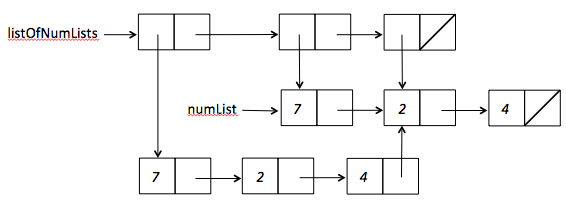
However, if we just enter the printed representation
'((7 2 4 2 4) (7 2 4) (2 4))forlistOfNumLists, that would create 13 cons cells: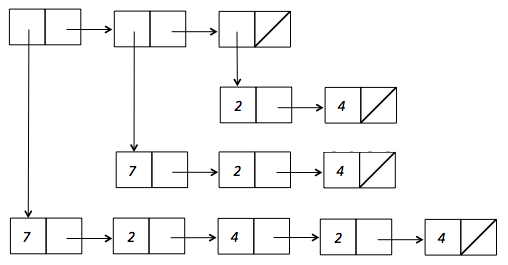
-
(2 points) How many cons cells would there be in the result of
(partial-reverses (range 1 1001))? -
(5 points) Complete the following definition of
partial-reverses-iterateso that it usesiterate-applyto iteratively calculate the same result (including sharing) aspartial-reverses:(define (partial-reverses-iterate xs) (iterate-apply ; expression1 ; expression2 ; expression3 ; expression4 ))In your expressions, the only functions you may use are
list,cons,first,rest,null, andnull?.Recall that
iterate-applyis defined as follows:(define (iterate-apply next done? finalize state) (if (apply done? state) (apply finalize state) (iterate-apply next done? finalize (apply next state)))) -
(5 Points) Complete the following definition of
partial-reverses-foldlso that it usesfoldlto iteratively calculate the same result (including sharing) aspartial-reverses:(define (partial-reverses-foldl xs) (foldl ; expression1 ; expression2 xs))In your expressions, the only functions you may use are
list,cons,first, andnull.
3. Solo Problem: Diagonal Pairs (17 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
In this problem, you will extend the yourAccountName-ps6-solo.rkt you created in Problem 1. This problem concerns one of the provided functions in that file:
(define (diagonal-pairs n) ; Assume is n a nonnegative integer
(foldr append null
(map (λ (sum)
(map (λ (fst) (cons fst (- sum fst)))
(range 0 (+ sum 1))))
(range 0 (+ n 1)))))-
(3 points) The
diagonal-pairsfunction generates a list of pairs of integers related to inputn, in a very particular order. Carefully describe in English the output list of pairs in terms ofn. As in PS5 Problem 4a, do not describe the Racket code or algorithm that generates the pairs. Instead, specify (1) exactly what pairs are in the output list (in a general way, not giving examples) and (2) exactly what order the pairs are in. Your description must be precise enough that someone else could implement thediagonal-pairsfunction correctly based on your description, without seeing the original Racket definition. -
(6 points) Recall the
genlistfunction from lecture (which is supplied as a helper function inyourAccountName-ps6-solo.rkt).(define (genlist next done? keepDoneValue? seed) (if (done? seed) (if keepDoneValue? (list seed) null) (cons seed (genlist next done? keepDoneValue? (next seed)))))In the file
yourAccountName-ps6-solo.rkt, define a Racket functiondiagonal-pairs-genlistthat has the same input-output behavior asdiagonal-pairsbut is defined usinggenlistby fleshing out the missing expressions in curly braces in the following skeleton:(define (diagonal-pairs-genlist n) ; Assume is n a nonnegative integer (genlist {next function goes here} {done? function goes here} {keepDoneValue? boolean goes here} {seed goes here})) -
(8 points) In the file
yourAccountName-ps6-solo.rkt, define a tail-recursive Racket functiondiagonal-pairs-iterthat has the same input-output behavior asdiagonal-pairsbut is defined iteratively using tail-recursive helper functions. Unlike thediagonal-pairs-genlistfunction, which add pairs from the front of the list to the end, yourdiagonal-pairs-iterimplementation should add pairs from the end of the list to the beginning.For full credit, your definition should flesh out this exact skeleton:
(define (diagonal-pairs-iter n) ; Assume is n a nonnegative integer (define (outer-tail {outer-parameters}) (define (inner-tail {inner-parameters}) {inner-body}) ; call inner_tail and outer-tail tail-recursively in inner-body {outer-body) ; call inner_tail tail-recursively in outer-body (outer-tail ...)Substantial partial credit can be earned for other iterative solutions that use tail recursion, such as solutions that use a single tail-recursive helper function.
Notes:
-
You should not use
iterateoriterate-applyin this problem! Instead, you should define one or more tail-recursive functions specialized for this particular problem. -
You should not perform any list reversals in your
diagonal-pairs-iterdefinition. -
The
diagonal-pairs-iterfunction need not itself be recursive; it can call one or more tail-recursive functions. -
As in PS5 Problem 4d, it may be helpful to use iteration tables involving concrete examples to help you define your tail recursive function(s).
-
4. Higher-order List Operators in SML (25 points)
In this problem, you will revisit several of the higher-order list operators we have studied in Racket in the context of SML. Since you are already familiar with these operators, your focus in this problem is on SML syntax and type-checking, rather than on the operators themselves.
Write all of your SML code in a new file named yourAccountName-ps6-holo.sml.
-
range,alts,cartesianProduct(9 points) Translate the following Racketrange,alts, andcartesian-productfunctions into SMLrange,alts, andcartesianProductfunctions:(define (range lo hi) (if (<= hi lo) null (cons lo (range (+ 1 lo) hi)))) (define (alts xs) (foldr (λ (x subResult) (list (cons x (second subResult)) (first subresult))) (list '() '()) xs (define (my-cartesian-product xs ys) (foldr (λ (x subres) (append (map (λ (y) (cons x y)) ys) subres)) null xs))For example:
val range = fn : int -> int -> int list val alts = fn : 'a list -> 'a list * 'a list val cartesianProduct = fn : 'a list -> 'b list -> ('a * 'b) list - range 0 10; val it = [0,1,2,3,4,5,6,7,8,9] : int list - range 3 8; val it = [3,4,5,6,7] : int list - range 5 5; val it = [] : int list - range 1 100; val it = [1,2,3,4,5,6,7,8,9,10,11,12,...] : int list - Control.Print.printLength := 100; - val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28, 29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53, 54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78, 79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99] : int list - alts [7, 5, 4, 6, 9, 2, 8, 3]; val it = ([7,4,9,8],[5,6,2,3]) : int list * int list - alts (range 0 20); val it = ([0,2,4,6,8,10,12,14,16,18],[1,3,5,7,9,11,13,15,17,19]) : int list * int list - cartesianProduct [1,2,3,4] ["a", "b", "c"]; val it = [(1,"a"),(1,"b"),(1,"c"),(2,"a"),(2,"b"),(2,"c"),(3,"a"),(3,"b"),(3,"c"), (4,"a"),(4,"b"),(4,"c")] : (int * string) list - cartesianProduct ["a", "b", "c"] [1,2,3,4]; val it = [("a",1),("a",2),("a",3),("a",4),("b",1),("b",2),("b",3),("b",4),("c",1), ("c",2),("c",3),("c",4)] : (string * int) listNotes:
-
You should do all your SML programming in Emacs within the
wxvirtual machine appliance. -
If you haven’t done so already, read these notes on SML/NJ and Emacs SML Mode and follow the advice there. In particular, it is strongly recommended that you create an SML interpreter within a
*sml*buffer in Emacs. Then you can useM-pandM-nto avoid retyping your test expressions. -
In all of your SML programming, do not use
#1,#2, etc. to extract tuple components orList.hd,List.tl, orList.nullto decompose and test lists. Instead, use pattern matching on tuples and lists, as illustrated in examples from lecture. -
Because hyphens are not allowed in SML identifiers, you should translate all hyphens in Racket identifiers either to underscores or camel case. E.g.,
cartesian-productin Racket becomescartesian_productorcartesianPrductin SML. -
Be careful with your explicit parentheses in SML. Many type errors in SML programs come from incorrectly parenthesizing expressions.
-
foldr,mapare both built into SML:val foldr = fn: ('a * 'b -> 'b) -> 'b -> 'a list -> 'b val map = fn: ('a -> 'b) -> 'a list -> 'b list -
Racket’s
appendtranslates to SML’s infix@operator, but when you want to pass it as an argument to a first-class function you write it asop@. -
In this entire problem (not just this part) some instances of Racket’s
conswill translate to SML’s infix list-prepending operator::, while others will translate to the tupling notation(<exp1>, <exp2>)for pair creation. Reason about SML types to figure out which to use when. SML’s type checker will yell at you if you get it wrong. -
In this entire problem (not just this part) some instances of Racket’s
listwill translate to SML’s lists while others will translate to SML’s tuples. Again, reason about SML types to figure out which to use when. -
Control.Print.printLengthcontrols how many list elements are displayed; after this number, ellipses are used. For example:- Control.Print.printLength := 5; val it = () : unit - range 0 20; val it = [0,1,2,3,4,...] : int list - Control.Print.printLength := 20; val it = () : unit - range 0 20; val it = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19] : int listAnother such control is
Control.Print.printDepth, which controls printing in nested lists. You won’t need that here, but will in Problem 5.
-
-
allContainMultipleandisSorted(8 points) Translate the following Racketall-contain-multiple?andsorted?functions into SMLdoAllContainMultpleandisSortedfunctions:(define (all-contain-multiple? m nss) (forall? (lambda (ns) (exists? (lambda (n) (divisible-by? n m)) ns)) nss)) (define (sorted? ns) (if (null ns) #t ; special case to avoid (rest ns) below (forall? (λ (pair) (<= (car pair) (cdr pair))) (zip ns (rest ns)))))For example:
- allContainMultiple 5 [[17,10,2],[25],[3,8,5]]; val it = true : bool - allContainMultiple 2 [[17,10,2],[25],[3,8,5]]; val it = false : bool - allContainMultiple 3 []; val it = true : bool - isSorted [7,4,2,5,4,6]; val it = false : bool - isSorted [2,3,3,5,6,7]; val it = true : bool - isSorted [2]; val it = true : bool - isSorted []; val it = true : bool - isSorted (range 0 1000); val it = true : bool - isSorted ((range 0 1000) @ [1001,1000]); val it = false : boolNotes:
-
SML includes the following analogs of
forall?,exists?, andzipthat you should use in your definitions:- List.all; val it = fn : ('a -> bool) -> 'a list -> bool - List.exists; val it = fn : ('a -> bool) -> 'a list -> bool - ListPair.zip; val it = fn : 'a list * 'b list -> ('a * 'b) list -
Because SML does not allow
?in identifiers, Racket names containing?need to be be transformed, as insorted?toisSorted -
The
List.andListPair.indicate that these functions come from modules. Here is documentation on theListmodule, and here is documentation on theListPairmodule.
-
-
genlist(8 points) Translate the following Racketgenlistandpartial-sums-tablefunctions into SMLgenlistandpartialSumsTablefunctions:(define (genlist next done? keepDoneValue? seed) (if (done? seed) (if keepDoneValue? (list seed) null) (cons seed (genlist next done? keepDoneValue? (next seed))))) (define (partial-sums-table ns) (genlist (λ (nums&ans) (list (rest (first nums&ans)) (+ (first (first nums&ans)) (second nums&ans)))) (λ (nums&ans) (null? (first nums&ans))) #t (list ns 0)))For example:
val genlist = fn : ('a -> 'a) -> ('a -> bool) -> bool -> 'a -> 'a list val pairs_genlist = fn : int -> (int * int) list - genlist (fn n => n * 2) (fn n => n > 1000) true 1; val it = [1,2,4,8,16,32,64,128,256,512,1024] : int list - genlist (fn n => n * 2) (fn n => n > 1000) false 1; val it = [1,2,4,8,16,32,64,128,256,512] : int list - partialSumsTable [7, 2, 5, 8, 4]; val it = [([7,2,5,8,4],0),([2,5,8,4],7),([5,8,4],9),([8,4],14),([4],22),([],26)] : (int list * int) list - partialSumsTable (range 1 11); val it = [([1,2,3,4,5,6,7,8,9,10],0),([2,3,4,5,6,7,8,9,10],1),([3,4,5,6,7,8,9,10],3), ([4,5,6,7,8,9,10],6),([5,6,7,8,9,10],10),([6,7,8,9,10],15),([7,8,9,10],21), ([8,9,10],28),([9,10],36),([10],45),([],55)] : (int list * int) listNotes:
-
SML does not allow
?in identifiers, so translatedone?tois_doneorisDoneand similarly withkeepDoneValue? -
An earlier version of this pset had an incorrect type for genlist that was missing the type for the bool argument::
val genlist = fn : ('a -> 'a) -> ('a -> bool) -> 'a -> 'a listThe correct type for genlist is:
val genlist = fn : ('a -> 'a) -> ('a -> bool) -> bool -> 'a -> 'a listThanks to Naomi Day for catching this bug.
-
Use pattern matching on tuples when translating the
(λ (nums&ans) ...)functions. Translate these to(fn (nums,ans) => ...). Because of SML’s built-in pattern matching, in SML it is unnecessary to have a separate function like Racket’siterate-applyin SML since the function arguments in SML’sgenlistcan already do pattern matching.
-
5. 2-3 Trees (25 points)
In this problem you will use SML to implement aspects of 2-3 trees, a particular search tree data structure that is guaranteed to be balanced.
Begin by skimming pages 1 through 7 of this handout on 2-3 trees. (I create this handout for CS230 in Fall, 2004, but we no longer teach 2-3 trees in that course).
In a 2-3 tree, there are three kinds of nodes: leaves, 2-nodes, and 3-nodes. Together, these can be expressed in SML as follows:
datatype TTTree = (* 2-3 tree of ints *)
L (* Leaf *)
| W of TTTree * int * TTTree (* tWo node *)
| H of TTTree * int * TTTree * int * TTTree (* tHree node *)For simplicity, we will only consider 2-3 trees of integers, though they can be generalized to handle any type of value.
For conciseness in constructing and displaying large trees, the three constructors have single-letter names. For example, below are the pictures of four sample 2-3 trees from the handout and how they would be expressed with these constructors:
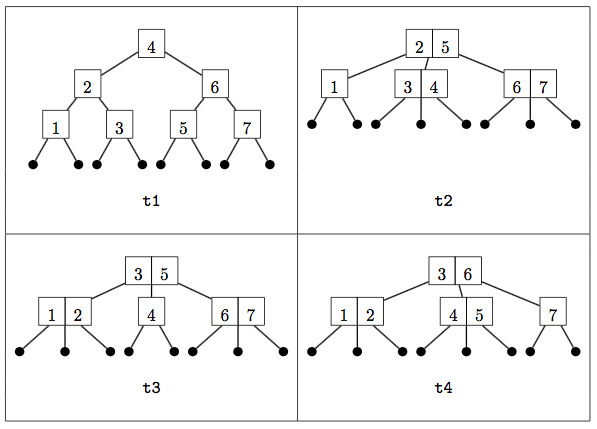
val t1 = W( W(W(L,1,L), 2, W(L,3,L)), 4, W(W(L,5,L), 6, W(L,7,L)))
val t2 = H( W(L,1,L), 2, H(L,3,L,4,L), 5, H(L,6,L,7,L))
val t3 = H( H(L,1,L,2,L), 3, W(L,4,L), 5, H(L,6,L,7,L))
val t4 = H( H(L,1,L,2,L), 3, H(L,4,L,5,L), 6, W(L,7,L))As explained in the handout on 2-3 trees, a 2-3 tree is only valid it it satisfies two additional properties:
- The ordering property:
- In a 2-node with left subtree l, value X, and right subtree r, (all values in l) ≤ X ≤ (all values in r).
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, (all values in l) ≤ X ≤ (all values in m) ≤ Y ≤ (all values in r).
- The height property (called path length invariant in the handout): in a 2-node or 3-node, the height of all subtrees must be exactly the same.
The height property guarantees that a valid 2-3 tree is balanced. Together, these two properties guarantee that a 2-3 tree is efficiently searchable.
Your ~wx/cs251/sml/ps6 folder includes the file TTTree.sml, which contains the TTTree dataytype defined above as well as numerous examples of valid and invalid 2-3 trees that are instances of this datatype. Note that t and vt are used for valid trees, io is used for invalidly ordered trees, and ih is used for invalid height trees.
| tree name | elements | ordered? | satisfies the height property? |
|---|---|---|---|
| t1 | [1,…,7] | Yes | Yes, with height 3 |
| t2 | [1,…,7] | Yes | Yes, with height 2 |
| t3 | [1,…,7] | Yes | Yes, with height 2 |
| t4 | [1,…,7] | Yes | Yes, with height 2 |
| vt0 | [] | Yes | Yes, with height 0 |
| vt2 | [1,2] | Yes | Yes, with height 1 |
| vt17 | [1,…,17] | Yes | Yes, with height 3 |
| vt20 | [1,…,20] | Yes | Yes, with height 4 |
| vt44 | [1,…,44] | Yes | Yes, with height 5 |
| vt92 | [1,…,92] | Yes | Yes, with height 6 |
| io2 | [1,2] | No | Yes, with height 1 |
| io7 | [1,…,7] | No | Yes, with height 2 |
| io17 | [1,…,17] | No | Yes, with height 3 |
| io20 | [1,…,20] | No | Yes, with height 4 |
| io44 | [1,…,44] | No | Yes, with height 5 |
| io92 | [1,…,92] | No | Yes, with height 6 |
| ih2 | [1,2] | Yes | No |
| ih7 | [1,…,7] | Yes | No |
| ih17 | [1,…,17] | Yes | No |
| ih20 | [1,…,20] | Yes | No |
| ih44 | [1,…,44] | Yes | No |
| ih92 | [1,…,92] | Yes | No |
These trees are used to define two lists:
val validTrees = [vt0, vt2, t2, t3, t4, t1, vt17, vt20, vt44, vt92]
val invalidTrees = [io2, io7, io17, io20, io44, io92,
ih2, ih9, ih17, ih20, ih44, ih92]In this problem you will (1) implement a validity test for 2-3 trees and (2) implement the effcient 2-3 insertion algorithm from the handout on 2-3 trees.
Your ~wx/cs251/sml/ps6 folder also includes the starter file TTTreeFuns.sml. In this file, flesh out the missing definitions as specified below. When you finish this problem, rename the file to yourAccountName-TTTreeFuns.sml before you submit it.
Be sure to perform execute the following in a shell in your wx appliance to get the ~wx/cs251/sml/ps6 folder:
cd ~/cs251/sml
git pull origin master-
satisfiesOrderingProperty(7 points)In this part, you will implement a function
satisfiesOrderingProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree ordering property andfalseif it does not. An easy way to do this is to define two helper functions:elts: TTTree -> int listreturns a list of all the elements of the tree in in-order — i.e.,- In a 2-node with left subtree l, value X, and right subtree r, all values in l are listed before X, which is listed before all elements in r.
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, all values in l are listed before X, which is listed before all values in m, which are listed before Y , which is listed before all values in r.
isSorted: int list -> boolreturnstrueif the list of integers is in sorted order andfalseotherwise.
For example:
- elts vt17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] : int list - elts io17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,17,16] : int list - isSorted(elts vt17); val it = true : bool - isSorted(elts io17); val it = false : boolUsing these two helper functions,
satisfiesOrderingPropertycan be implemented as:fun satisfiesOrderingProperty t = isSorted(elts t)For example:
- map satisfiesOrderingProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesOrderingProperty invalidTrees; val it = [false,false,false,false,false,false,true,true,true,true,true,true] : bool listNotes:
-
Once (and only once) execute
use "TTTree.sml";to load the
TTTreedatatype and example trees. Then every time you change the fileTTTreeFuns.sml, executeuse "TTTreeFuns.sml" -
If you haven’t done so already, read these notes on SML/NJ and Emacs SML Mode and follow the advice there. In particular, it is strongly recommended that you create an SML interpreter within a
*sml*buffer in Emacs. Then you can useM-pandM-nto avoid retyping your test expressions. -
You may need to execute
Control.Print.printLength := 100;in order to see all the list elements. -
Implement
isSortedusing the same zipping approach you used in PS3. You do zipping in SML viaListPair.zipfrom the ListPair module.List.allfrom the List module is also helpful.
-
satisfiesHeightProperty(6 points)In this part, you will implement a function
satisfiesHeightProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree height property andfalseif it does not. An easy way to do this is to definesatisfiesHeightPropertyasfun satisfiesHeightProperty t = Option.isSome (height t)where
Option.isSomeis a function from the Option module that determines if anoptionvalue is aSOME(vs. aNONE) andheightis a function with typeTTTree -> option intsuch thatheight treturnsSOME hiftsatisfies the height property with heighthand otherwise returnsNONE.Implement the
heightfunction by fleshing out this skeleton:(* height: TTTree -> int option *) fun height L = (* return an appropriate option value here *) | height (W(l, _, r)) = (case (height(l), height(r)) of (* put appropriate pattern clauses here *)) | (* handle the H case here, similarly to the W case *)For example:
- map height validTrees; val it = [SOME 0,SOME 1,SOME 2,SOME 2,SOME 2,SOME 3,SOME 3,SOME 4,SOME 5,SOME 6] : int option list - map height invalidTrees; val it = [SOME 1,SOME 2,SOME 3,SOME 4,SOME 5,SOME 6,NONE,NONE,NONE,NONE,NONE,NONE] : int option listNotes:
-
It’s important to enclose the
caseexpressions withinheightin parens to distinguish the pattern clauses of thecaseexpression from those of theheightfunction definition. -
Once
heightis defined,satisfiesHeightPropertyis defined:- map satisfiesHeightProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesHeightProperty invalidTrees; val it = [true,true,true,true,true,true, false,false,false,false,false,false] : bool list -
Once both
satisfiesOrderingPropertyandsatisfiesHeightPropertyare defined, it is trivial to define a functionisValid: TTTree -> boolthat returnstrueif a given 2-3 tree is valid andfalseotherwise.fun isValid t = satisfiesOrderingProperty t andalso satisfiesHeightProperty t - map isValid validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map isValid invalidTrees; val it = [false,false,false,false,false,false, false,false,false,false,false,false] : bool list
-
-
insert(12 points) In this part, you will implement the insertion algorithm for 2-3 trees as described on pages 3 to 5 of the handout on 2-3 trees. You will not implement the special cases described on page 6 .The insertion algorithm is a recursive algorithm that uses the notion of a pseudo 2-node that is “kicked up” in certain cases and handled specially in the upward phase of the recursion. To distinguish an insertion result that is a regular 2-3 tree from a pseudo 2-node that is “kicked up”, we use the following datatype:
datatype InsResult = Tree of TTTree | KickedUp of TTTree * int * TTTree (* pseudo 2-node "kicked up" from below *)You will implement 2-3 tree insertion via a pair of functions:
-
(insert v t)returns the newTTTreethat results from inserting a given intvinto a given treet.inserthas typeint -> TTTree -> TTTree. -
(ins v t)is a helper function that returns the instance ofInsResultthat results from inserting a given intvinto a given treet.inshas typeint -> TTTree -> InsResult.
Your implementation should flesh out the following code skeleton by turning the pictures on pages 3 to 5 from the handout on 2-3 trees into SML code.
(* insert: int -> TTTree -> TTTree *) fun insert v t = case ins v t of Tree t => t | KickedUp(l, w, r) => W(l, w, r) and (* "and" glues together mutually recursive functions *) (* ins: int -> TTTree -> InsResult *) ins v L = KickedUp (L, v, L) | ins v (W(l, X, r)) = if v <= X then (case ins v l of Tree l' => Tree(W(l', X, r)) | KickedUp (l', w, m) => Tree(H(l', w, m, X, r))) else (* flesh this out *) | (* handle an H node similarly to the W node based on rules from the handout *)Notes:
-
The
insfunction should only callinsrecursively and should not callinsert. -
An easy way to test
insertis to call the followinglistToTTTreefunction on a list of numbers generated byrange. (These are already defined in your starter file.) Note that you may need to increase the print depth (viaControl.Print.printDepth := 100) in order to see all the details of the printed trees:fun listToTTTree xs = foldl (fn (x,t) => insert x t) L xs fun range lo hi = if lo >= hi then [] else lo :: (range (lo + 1) hi) - listToTTTree (range 1 8); val it = W (W (W #,2,W #),4,W (W #,6,W #)) : TTTree - listToTTTree (range 1 17); val it = W (W (W #,4,W #),8,W (W #,12,W #)) : TTTree - Control.Print.printDepth := 100; val it = () : unit - listToTTTree (range 1 7); val it = H (W (L,1,L),2,W (L,3,L),4,H (L,5,L,6,L)) : TTTree - listToTTTree (range 1 18); val it = W (W (W (W (L,1,L),2,W (L,3,L)),4,W (W (L,5,L),6,W (L,7,L))),8, W (W (W (L,9,L),10,W (L,11,L)),12, H (W (L,13,L),14,W (L,15,L),16,W (L,17,L)))) : TTTree - listToTTTree (range 1 45); val it = W (W (W (W (W (L,1,L),2,W (L,3,L)),4,W (W (L,5,L),6,W (L,7,L))),8, W (W (W (L,9,L),10,W (L,11,L)),12,W (W (L,13,L),14,W (L,15,L)))),16, H (W (W (W (L,17,L),18,W (L,19,L)),20,W (W (L,21,L),22,W (L,23,L))),24, W (W (W (L,25,L),26,W (L,27,L)),28,W (W (L,29,L),30,W (L,31,L))),32, H (W (W (L,33,L),34,W (L,35,L)),36,W (W (L,37,L),38,W (L,39,L)),40, W (W (L,41,L),42,H (L,43,L,44,L))))) : TTTree -
Unfortunately, inserting elements in sequential order as above tends to create 2-3 trees with almost all 2-nodes and very few 3-nodes. It turns out a better way is to mix up the order of insertion as is done in the following code for
makeTTTree. This results in trees that have a good mix of 2-nodes and 3-nodes:(* Return list that has all ints in nums, but those not divisible by 3 come before those divisible by three *) fun arrangeMod3 nums = let val (zeroMod3, notZeroMod3) = List.partition (fn n => (n mod 3) = 0) nums in notZeroMod3 @ zeroMod3 end (* Make a 2-3 tree with elements from 1 up to and including size. Use arrangeMod3 to mix up numbers and lead to more 3-nodes than we'd get with sorted integers lists *) fun makeTTTree size = listToTTTree (arrangeMod3 (range 1 (size + 1))) - makeTTTree 17; val it = H (W (W (L,1,L),2,H (L,3,L,4,L)),5,W (H (L,6,L,7,L),8,H (L,9,L,10,L)),11, H (H (L,12,L,13,L),14,W (L,15,L),16,W (L,17,L))) : TTTree - makeTTTree 44; val it = W (W (W (W (W (L,1,L),2,H (L,3,L,4,L)),5,W (H (L,6,L,7,L),8,H (L,9,L,10,L))), 11, W (W (H (L,12,L,13,L),14,H (L,15,L,16,L)),17, W (H (L,18,L,19,L),20,H (L,21,L,22,L)))),23, W (W (W (H (L,24,L,25,L),26,H (L,27,L,28,L)),29, W (H (L,30,L,31,L),32,H (L,33,L,34,L))),35, W (W (H (L,36,L,37,L),38,H (L,39,L,40,L)),41, W (W (L,42,L),43,W (L,44,L))))) : TTTree -
Finally, to test your insertion implementation more extensively, try
(testInsert 1000)with the following function, which will usemakeTTTreeto create 2-3 trees containing 0 elements to 1000 elements and warn you of any invalid trees.fun testInsert upToSize = let val pairs = map (fn n => (n, makeTTTree n)) (range 0 (upToSize + 1)) val (validPairs, invalidPairs) = List.partition (fn (_,t) => isValid t) pairs val wrongElts = List.filter (fn (n,t) => (elts t) <> (range 1 (n + 1))) validPairs in if (null invalidPairs) andalso (null wrongElts) then (print "Passed all test cases\n"; []) else if (not (null invalidPairs)) then (print "There are invalid trees in the following cases\n"; invalidPairs) else (print "The elements or element order is wrong in the following cases\n"; wrongElts) end - testInsert 1000; Passed all test cases val it = [] : (int * TTTree) list
-
Extra Credit: 2-3 Tree Deletion (20 points)
In SML, implement and test the 2-3 tree deletion algorithm presented in pages 8 through 11 of the handout on 2-3 trees.
Extra Credit: 2-3 Trees in Java (35 points)
Implement and test 2-3 tree insertion and deletion in Java. Compare the SML and Java implementations. Which features of which languages make the implementation easier and why?