PS6: Practicing PostFix
- Due: Tuesday, March 20, 2018
- Notes:
- This pset contains two solo problems worth 50 points.
- This pset has 100 total points.
- The problems needn’t be done in order. Feel free to jump around.
- Although PS6 is officially due on Tuesday, March 20, no lateness coupons will be required until Tuesday, April 03. Submitting by Monday, April 02 requires no lateness coupons; submitting on Tuesday, April 03 requires 1 lateness coupon; and one more lateness coupon is required per day after Tuesday, April 03.
- PS7 will be posted during break and will be due on Tuesday, April 10. You are not expected to work on it during break, but it is being made available for anyone who might want to get ahead.
-
Times from Fall ‘17
The following times do not include Solo Problem 2. Although I have given this problem in a previous semester, I do not have time statistics for that semester.
Times Problem 1 Problem 3 Problem 4 Problem 5 Total (Excluding Problem 2) average time (hours) 1.78 0.69 0.61 2.12 4.94 median time (hours) 2.00 0.50 0.50 2.00 5.00 max time (hours) 3.16 1.50 1.50 3.33 7.90 Notes
- Submission:
- In your yourFullName CS251 Spring 2018 Folder, create a Google Doc named yourFullName CS251 PS6.
- At the top of your yourFullName CS251 PS6 doc, include your name, problem set number, date of submission, and an approximation of how long each problem part took.
- For all parts of all problems, include all answers (including Racket code) in your PS6 google doc. Format Racket code using a fixed-width font, like Consolas or Courier New. You can use a small font size if that helps.
- For Solo Problems 1 and 2:
- Include the English answers to part 1a in your PS6 google doc.
- Be sure that all function definitions in
yourAccountName-ps6-solo.rktalso appear in your Google Doc (so that I can comment on them) - Drop a copy of your
yourAccountName-ps6-solo.rktin your~/cs251/drop/ps06drop folder oncs.wellesley.edu.
- For Problem 3:
- Be sure that your
n-folddefinition inyourAccountName-ps6-n-fold.rktalso appears in your Google Doc. - Drop a copy of your
yourAccountName-ps6-n-fold.rktin your~/cs251/drop/ps06drop folder oncs.wellesley.edu.
- Be sure that your
- For Problem 4:
- Be sure that your
deep-reversedefinition inyourAccountName-ps6-deep-reverse.rktalso appears in your Google Doc. - Drop a copy of your
yourAccountName-ps6-deep-reverse.rktin your~/cs251/drop/ps06drop folder oncs.wellesley.edu.
- Be sure that your
- For Problem 4:
- Include the modified parts of
yourAccountName-ps6-postfix.rktin your Google Doc. (You only need to include the modified parts, not the entire contents of the PostFix interpreter!) - Drop a copy of your
yourAccountName-ps6-postfix.rktin your~/cs251/drop/ps06drop folder oncs.wellesley.edu.
- Include the modified parts of
1. Solo Problem: Diagonal Duples (22 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
Begin this problem by downloading this starter file ps6-solo-starter.rkt, which you should rename to yourAccountName-ps6-solo.rkt. This file contains provided definitions for this solo problem.
This problem concerns one of the provided functions in yourAccountName-ps6-solo.rkt.
(define (diagonal-duples n) ; Assume is n a nonnegative integer
(foldr append null
(map (λ (sum)
(map (λ (fst) (list fst (- sum fst)))
(range 0 (+ sum 1))))
(range 0 (+ n 1)))))-
(3 points) The
diagonal-duplesfunction generates a list of duples (2-element lists) of integers related to inputn, in a very particular order. Carefully describe in English the output list of duples in terms ofn. As in PS5 Problem 3a, do not describe the Racket code or algorithm that generates the duples. Instead, specify (1) exactly what duples are in the output list (in a general way, not giving examples) and (2) exactly what order the duples are in. Your description must be precise enough that someone else could implement thediagonal-duplesfunction correctly based on your description, without seeing the original Racket definition. (You should carefully study the PS4 Problem 3a solution before starting this problem.) -
(5 points) Recall the
genlist-applyfunction from lecture and PS5 (which is supplied as a helper function inyourAccountName-ps6-solo.rkt).(define (genlist-apply next done? keepDoneValue? seed) (if (apply done? seed) (if keepDoneValue? (list seed) null) (cons seed (genlist-apply next done? keepDoneValue? (apply next seed)))))In the file
yourAccountName-ps6-solo.rkt, define a Racket functiondiagonal-duples-genlist-applythat has the same input-output behavior asdiagonal-duplesbut is defined usinggenlist-applyby fleshing out the missing expressions denoted by the quoted symbols in the following skeleton:(define (diagonal-duples-genlist-apply n) ; Assume is n a nonnegative integer (genlist-apply 'next-function-goes-here 'done-function-goes-here 'keep-done-value-goes-here 'seed-goes-here )) -
(6 points) Recall the
iterate-applyfunction from lecture and PS5 (which is supplied as a helper function inyourAccountName-ps6-solo.rkt).(define (iterate-apply next done? finalize state) (if (apply done? state) (apply finalize state) (iterate-apply next done? finalize (apply next state))))In the file
yourAccountName-ps6-solo.rkt, define a Racket functiondiagonal-duples-iterate-applythat has the same input-output behavior asdiagonal-duplesbut is defined usingiterate-applyby fleshing out the missing expressions denoted by the quoted symbols in the following skeleton:(define (diagonal-duples-iterate-apply n) ; Assume is n a nonnegative integer (iterate-apply 'next-function-goes-here 'done?-function-goes-here 'finalize-function-goes-here 'initial-state-goes-here ))Notes:
-
Unlike the
diagonal-duples-genlist-applyfunction, which add duples from the front of the list to the end, yourdiagonal-duples-iterate-applyimplementation should add duples from the end of the list to the beginning. -
In this function you should not use
snoc,append, orreverseon any lists. You should only useconsto extend a list. Why? Because repeatedsnocing leads to quadratic running times. How? By constructing the desired output list in reverse, starting with the last duple and working your way back to the first duple. -
As in PS5 Problem 3d, it may be helpful to use iteration tables involving concrete examples to help you define this function.
-
-
(8 points) In the file
yourAccountName-ps6-solo.rkt, define a tail-recursive Racket functiondiagonal-duples-iterthat has the same input-output behavior asdiagonal-duplesbut is defined iteratively using tail-recursive helper functions.For full credit, your definition should flesh out this exact skeleton:
(define (diagonal-duples-iter n) ; Assume is n a nonnegative integer (define (outer-tail {outer-parameters}) (define (inner-tail {inner-parameters}) {inner-body}) ; call inner_tail and outer-tail tail-recursively in inner-body {outer-body) ; call inner_tail tail-recursively in outer-body (outer-tail ...)Substantial partial credit can be earned for other iterative solutions that use tail recursion, such as solutions that use a single tail-recursive helper function.
Notes:
-
Unlike the
diagonal-duples-genlist-applyfunction, which add duples from the front of the list to the end, yourdiagonal-duples-iterimplementation should add duples from the end of the list to the beginning (like -
For the same reasons as in
diagonal-duples-iterate-apply, in this function you should not usesnoc,append, orreverseon any lists. -
IMPORTANT: Just naming a function to end in
-taildoes not make it tail recursive! In order to be tail recursive, all calls of your tail recursive functions must not be subexpressions of other function calls. E.g. in the code(if <test> <then> (outer-tail (inner-tail ...) ...))the call to
outer-tailis a tail call, but the the call toinner-tailis not a tail call (because it is a subexpression of another call).
-
2. Solo Problem: Down and Up Recursions (28 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
In this problem, you will put all your code in the yourAccountName-ps6-solo.rkt file you created in Solo Problem 1.
We have seen that a list recursion can have both a down phase (in which values may be accumulated as the elements are processed left-to-right) and an up phase (in which values may be accumulated as the elements are processed right-to-left). It is even possible in a single recursion over a list of elements to combine those elements and the intermediate results of the down and up accumulations in interesting ways.
In this problem we will consider a function (down-and-up nums) that is an example of such a list recursion over a list of integers nums.
To understand what down-and-up does, we’ll define the partial sum list of a list of numbers to be the partial sums of the numbers in a left-to-right summation of the elements. E.g., the partial sum list of '(1 2 3 4 5) is '(1 3 6 10 15), the partial sum list of '(2 4 5 1 3) is '(2 6 11 12 15), and the partial sum list of '(8 2 1 16 4 1) is '(8 10 11 27 31 32).
(down-and-up nums) returns a list of 3 elements:
-
The first element of the resulting list is a list whose elements are the elements of
numsscaled by the corresponding elements of the partial sum list ofnums. For example:- When nums is
'(1 2 3 4 5), the partial sum list is'(1 3 6 10 15), so the scaled list is'(1 6 18 40 75). - When nums is
'(2 4 5 1 3), the partial sum list is'(2 6 11 12 15), so the scaled list is'(4 24 55 12 45). - When nums is
'(8 2 1 16 4 1), the partial sum list is'(8 10 11 27 31 32), so the scaled list is'(64 20 11 432 124 32). - When nums is
'(8 2 17 4 1), the partial sum list is'(8 10 27 31 32), so the scaled list is'(64 20 459 124 32).
- When nums is
-
The second element of the resulting list is the sum of the elements in
nums. For example, both'(1 2 3 4 5)and'(2 4 5 1 3)have sum15, while'(8 2 1 16 4 1)has sum32. -
The third element of the resulting list is a list of booleans that indicate which elements of
numsevenly divide the sum of the elements innums. For example:- When nums is
'(1 2 3 4 5), the boolean list is'(#t #f #t #f #t), because 1, 3, and 5 divide 15 but 2 and 4 do not. - When nums is
'(2 4 5 1 3), the boolean list is'(#f #f #t #t #t)for the same reason. - When nums is
'(8 2 1 16 4 1), the boolean list is'(#t #t #t #t #t #t)because all of the elements divide 32.
- When nums is
So here are examples of down-and-up:
> (down-and-up '(1 2 3 4 5))
'((1 6 18 40 75) 15 (#t #f #t #f #t))
> (down-and-up '(2 4 5 1 3))
'((4 24 55 12 45) 15 (#f #f #t #t #t))
> (down-and-up '(8 2 1 16 4 1))
'((64 20 11 432 124 32) 32 (#t #t #t #t #t #t))
> (down-and-up '(8 2 12 4 6))
'((64 20 264 104 192) 32 (#t #t #f #t #f))
> (down-and-up '(8 2 17 4 1))
'((64 20 459 124 32) 32 (#t #t #f #t #t))-
(8 points) Define the
down-and-upfunction by fleshing out the skeleton of thedown-and-up-helperfunction in the following skeleton. Yourdown-and-up-helperfunction should be recursive and should make only one pass over the list. You should not use any higher-order list functions or any helper functions other thandivisible-by?in your definition.(define (down-and-up nums) (down-and-up-helper 0 nums)) (define (down-and-up-helper sumSoFar ns) (if (null? ns) ; put expression 1 here ; put expression 2 here ))Notes:
-
You should not need to use any list operators other than
first,second,third,rest,cons, andlist. In particular,appendis not necessary. -
Your definition should make exactly one recursive call to
down-and-up-helper; otherwise it would make more than one pass over the list. Also, if there is more than one such call, the definition will suffer from the problem withbad-maxlistshown in slides 9-17 through 9-19 of the slides on Local Naming and Scope. Using the strategy forgood-maxlistin slide 9-20, this problem can be solved by having only a single recursive call. Note: you will still get substantial partial credit in this problem if there are multiple recursive calls todown-and-up-helper. -
Below is an image showing all the operations that are performed in (down-and-up-helper 0 ‘(1 2 3 4 5)). Click here for a sequence of images animating the down and up phases of
down-and-up-helperin this example.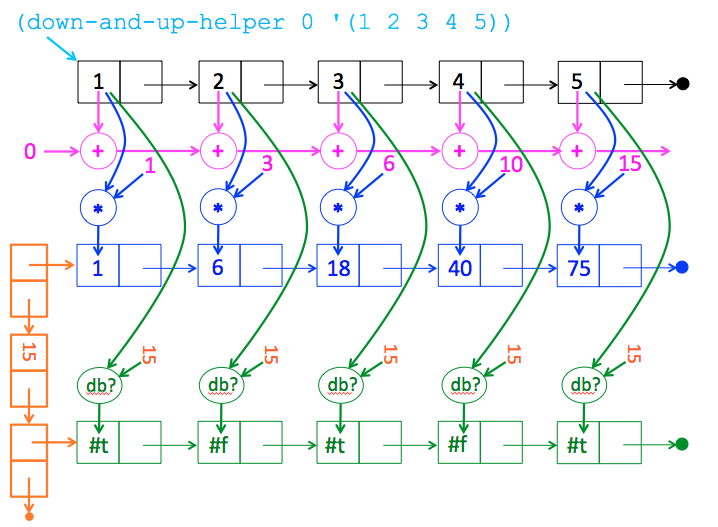
-
In the twelve images of the sequence, there are six calls to
down-and-up-helper. Two images are shown for each such call: one for the state of the system when the call is made, and one for the state of the system when it returns. I have modified the return slides to show the return value. Here are the six calls and their results. You can use these as six test cases fordown-and-up-helper:> (down-and-up-helper 15 '()) '(() 15 ()) > (down-and-up-helper 10 '(5)) '((75) 15 (#t)) > (down-and-up-helper 6 '(4 5)) '((40 75) 15 (#f #t)) > (down-and-up-helper 3 '(3 4 5)) '((18 40 75) 15 (#t #f #t)) > (down-and-up-helper 1 '(2 3 4 5)) '((6 18 40 75) 15 (#f #t #f #t)) > (down-and-up-helper 0 '(1 2 3 4 5)) '((1 6 18 40 75) 15 (#t #f #t #f #t))
-
-
(6 points) We can generalize
down-and-upinto a higher-order list functionfoldLRthat has aspects of bothfoldlandfoldr. The lettersLRat the end offoldLRhave been capitalized to emphasize them; since Racket identifiers are case-sensitive, they must be capitalized.(define (foldLR combineL state combineR nullfun xs) (if (null? xs) (nullfun state) (let ((next-state (combineL (car xs) state))) (combineR (first xs) next-state (foldLR combineL next-state combineR nullfun (rest xs))))))Give an alternative definition of
down-and-upnameddown-and-up-foldLRthat is implemented in terms offoldLRby fleshing out this skeleton:(define (down-and-up-foldLR nums) (foldLR ; put expression 1 here ; put expression 2 here ; put expression 3 here ; put expression 4 here nums))Notes:
-
To understand
foldLR, it may be helpful to review the definitions ofmy-foldrfrom slide 6-24 of the First-Class Functions in Racket slides and the definition ofmy-foldlfrom slide 8-25 of the Iteration Via Tail Recursion slides.foldLR’scombineLandstatecorrespond tocombinerandresultSoFarinmy-foldlfoldLR’scombineRandnullfunare generalizations ofcombineandnullvalinmy-foldr
-
In both parts 2b and 2c, keep in mind that it is often useful for a function to ignore one or more of its arguments. For example, consider the following:
(define (return17 x) 17) ; ignores argument and always returns 17 (define (add-first-and-last x y z) (+ x z)) ; ignores middle argument (define (foldr-ternop ternop null-value xs) ; standard definition of foldr-ternop (if (null? xs) null-value (ternop (first xs) (rest xs) (foldr-ternop ternop null-value (rest xs))))) > (return17 42) 17 > (map return17 (range 10)) '(17 17 17 17 17 17 17 17 17 17) > (add-first-and-last 1 20 300) 301 > (foldr-ternop add-first-and-last 0 (list 1 2 3 4)) 10 ; = 1 + 2 + 3 + 4 ; add-first-and-last ignore the second argument in the combiner of foldr-ternop
-
-
(12 points) Define versions of
foldl,foldr, andfoldr-ternopin terms offoldLRby fleshing out the following skeletons:(define (my-foldl combine state xs) (foldLR ; put expression 1 here ; put expression 2 here ; put expression 3 here ; put expression 4 here xs)) (define (my-foldr combine nullval xs) (foldLR ; put expression 1 here ; put expression 2 here ; put expression 3 here ; put expression 4 here xs)) (define (my-foldr-ternop ternop nullval xs) (foldLR ; put expression 1 here ; put expression 2 here ; put expression 3 here ; put expression 4 here xs))For example:
> (my-foldl cons (list) (list 1 2 3 4)) '(4 3 2 1) > (my-foldr cons (list 17) (list 1 2 3 4)) '(1 2 3 4 17) > (my-foldr-ternop (λ (fst rst subres) (cons (list fst rst) subres)) (list) (list 1 2 3 4)) '((1 (2 3 4)) (2 (3 4)) (3 (4)) (4 ()))Notes:
-
The idea here is that
foldLRis a generalization of bothfoldlandfoldr, and by passing it appropriate arguments, you can make it behave likefoldl,foldr, andfoldr-ternopin addition to expressing more complicated functions likedown-and-up. -
See the note in 2b about functions that ignore one or more of their arguments.
-
-
(2 points) After you define
my-foldlin terms offoldLR, you fall asleep and are visited in a dream by a spirit that calls itself “The Great Quux”. It tells you that a correctly-definedmy-foldlwill often return the same results asfoldl, but will fail to act likefoldlin a fundamental respect. You wake up in a cold sweat and realize the spirit is correct. Explain.
3. n-fold Composition (10 points)
In mathematics, the composition of unary functions f and g, writen f ◦g is the unary function such that (f ◦g)(x) = f(g(x)).
We can define a composition function o in Racket as follows:
(define (o f g)
(λ (x) (f (g x))))Here are some examples of composition:
(define (inc y) (+ y 1))
(define (dbl z) (* z 2))
> ((o inc dbl) 10)
21
> ((o dbl inc) 10)
22
> ((o inc inc) 10)
12
> ((o dbl dbl) 10)
40The identity function id is the identity of the composition operator:
(define (id x) x)
> ((o inc id) 10)
11
> ((o id inc) 10)
11The n-fold composition of a function f, written f n is f composed with itself n times. Thus, f 2 = f ◦ f, f 3 = f ◦ f ◦ f, and so on. Note that f 1 = f, and f 0 = the identity function id.
In this problem, you will define in a file named yourAccountName-ps6-n-fold.rkt a Racket function (n-fold n f) that takes a nonnegative integer n and a unary function f and returns the n-fold composition of f. In your definition, you may not use explicit recursion. There are many different ways to define n-fold without recursion! You are allowed to use higher-order functions we’ve studied (e.g., map, foldr, foldl, iterate, iterate-apply, genlist, genlist-apply) as well as standard Racket functions like range.
Here are some examples of using n-fold:
> ((n-fold 2 inc) 0)
2
> ((n-fold 17 inc) 100)
117
> ((n-fold 3 dbl) 1)
8
> ((n-fold 4 (curry + 3)) 0)
12
> ((n-fold 4 (curry * 3)) 1)
81
> ((n-fold 2 (o inc dbl)) 5)
23
> ((n-fold 2 (o dbl inc)) 5)
26
> ((n-fold 17 id) 42)
424. Deep Reverse (6 points)
We saw in lecture that tree recursion on trees represented as s-expressions could be expressed rather elegantly. For example:
(define (atom? x)
(or (number? x) (boolean? x) (string? x) (symbol? x)))
(define (sexp-num-atoms sexp)
(if (atom? sexp)
1
(foldr + 0 (map sexp-num-atoms sexp))))
> (sexp-num-atoms '((a (b c) d) e (((f) g h) i j k)))
11
> (sexp-num-atoms '(a b c d))
4
> (sexp-num-atoms 'a)
1
> (sexp-num-atoms '())
0
(define (sexp-atoms sexp)
(if (atom? sexp)
(list sexp)
(foldr append null (map sexp-atoms sexp))))
> (sexp-atoms '((a (b c) d) e (((f) g h) i j k)))
'(a b c d e f g h i j k)
> (sexp-atoms '(a b c d))
'(a b c d)
> (sexp-atoms 'a)
'(a)
> (sexp-atoms '())
'()In this problem, you will define a function (deep-reverse sexp) that returns a new s-expression in which the order of the children at every node of the s-expression tree sexp is reversed.
> (deep-reverse '((a (b c) d) e (((f) g h) i j k)))
'((k j i (h g (f))) e (d (c b) a))
> (deep-reverse '(a b c d))
'(d c b a)
> (deep-reverse 'a)
'a
> (deep-reverse '())
'()Notes:
-
Begin with this starter file ps6-deep-reverse-starter.rkt, which you should rename to
yourAccountName-ps6-deep-reverse.rkt. Add your definition ofdeep-reverseto this file. -
Your definition should have form similar to the definitions for
sexp-num-atomsandsexp-atoms, but you’ll want to use something other thanfoldr. -
You are not allowed to use
reversein your definition.
5. Extending PostFix (34 points)
In lecture we studied several different versions of an interpreter for the PostFix language implemented in Racket. This pset involves starting with the following version of the interpreter:
This is a slightly modified version of the file postfix-transform-fancy.rkt studied in lecture.
Begin by making a copy of ps6-postfix-starter.rkt named yourAccountName-ps6-postfix.rkt and load this into Dr. Racket. Near the bottom of this file is the following PostFix program named sos (for “sum of squares”). Racket’s semi-colon comments have been used to explain the commands in the program:
;; Sum-of-squares program
(define sos
'(postfix 2 ; let's call the arguments a and b, from top down
1 nget ; duplicate a at top of stack
mul ; square a
swap ; stack now has b and a^2 from top down
1 nget mul ; square b
add ; add b^2 + a^2 and return
))Let’s run the program on the arguments 5 and 12:
> (postfix-run sos '(5 12))
About to execute commands (1 nget mul swap 1 nget mul add) on stack (5 12)
after executing 1, stack is (1 5 12)
after executing nget, stack is (5 5 12)
after executing mul, stack is (25 12)
after executing swap, stack is (12 25)
after executing 1, stack is (1 12 25)
after executing nget, stack is (12 12 25)
after executing mul, stack is (144 25)
after executing add, stack is (169)
169Note that the stack that results from executing each command on the previous stack is displayed, line by line. This behavior is controlled by the print-stacks? flag at the top of the program:
(define print-stacks? #t)If we set the flag to #f, the intermediate stack display will be turned off:
(define print-stacks? #f)> (postfix-run sos '(5 12))
169Turn the print-stacks? flag on when it’s helpful to understand or debug a PostFix program.
-
(10 points)
Consider the following Racket function
gthat is defined near the bottom of the PostFix intepreter file:(define (g a b c) (- c (if (= 0 (remainder a 2)) (quotient b (- a c)) (* (+ b c) a))))In this part, your goal is to flesh out the definition of a three-argument PostFix program
pfgthat performs the same calculation asgon three arguments:(define pfg '(postfix 3 ;; Flesh out and comment the commands in this PostFix program ))Here are some examples with a correctly defined
pfg:> (apply g '(10 2 8)) 7 > (postfix-run pfg '(10 2 8)) 7 > (apply g '(-7 2 3)) 38 > (postfix-run pfg '(-7 2 3)) 38 > (apply g '(5 4 5)) -40 > (postfix-run pfg '(5 4 5)) -40Notes:
-
Please comment the commands in
pfglike those insos. -
You have been provided with a testing function
(test-pfg)that will test yourpfgfunction on 5 sets of arguments:;; Tests on an incorrect definition of pfg: > (test-pfg) Testing pfg on (10 2 8): ***different results*** g: 7 pfg: -7 Testing pfg on (11 2 8): ***different results*** g: -102 pfg: 102 Testing pfg on (-6 3 8): ***different results*** g: 8 pfg: -8 Testing pfg on (-7 2 3): ***different results*** g: 38 pfg: -38 Testing pfg on (5 4 5): ***different results*** g: -40 pfg: 40 ;; Tests on a correct definition of pfg: > (test-pfg) Testing pfg on (10 2 8): same result for g and pfg = 7 Testing pfg on (11 2 8): same result for g and pfg = -102 Testing pfg on (-6 3 8): same result for g and pfg = 8 Testing pfg on (-7 2 3): same result for g and pfg = 38 Testing pfg on (5 4 5): same result for g and pfg = -40
-
-
(7 points) Extend PostFix by adding the following two commands:
-
exp: given a stacki_base i_expt ...(wherei_baseandi_exptare integers), replacesi_baseandi_exptby the result of raisingi_baseto the power ofi_expt(or 0 ifi_exptis negative). -
chs: given a stacki_n i_k ...(wherei_kandi_nare nonnegative integers andi_k<=i_n), replacesi_nandi_kby the value ofi_nchoosei_k. (See the definition of “choose” notation here). If one or both ofi_nandi_kare invalid arguments, displays an error message (sees examples below).
For example:
> (postfix-run '(postfix 0 2 3 exp) '()) 8 > (postfix-run '(postfix 0 3 2 exp) '()) 9 > (postfix-run '(postfix 0 5 3 exp) '()) 125 > (postfix-run '(postfix 0 3 5 exp) '()) 243 > (postfix-run '(postfix 0 0 5 exp) '()) 0 > (postfix-run '(postfix 0 5 0 exp) '()) 1 > (postfix-run '(postfix 0 5 -1 exp) '()) 0 > (postfix-run '(postfix 0 3 -5 exp) '()) 0 > (postfix-run '(postfix 0 6 0 chs) '()) 1 > (postfix-run '(postfix 0 6 1 chs) '()) 6 > (postfix-run '(postfix 0 6 2 chs) '()) 15 > (postfix-run '(postfix 0 6 3 chs) '()) 20 > (postfix-run '(postfix 0 6 4 chs) '()) 15 > (postfix-run '(postfix 0 6 5 chs) '()) 6 > (postfix-run '(postfix 0 6 6 chs) '()) 1 > (postfix-run '(postfix 0 6 7 chs) '()) ERROR: invalid operands for chs (6 7) > (postfix-run '(postfix 0 6 -2 chs) '()) ERROR: invalid operands for chs (6 -2) > (postfix-run '(postfix 0 -6 3 chs) '()) ERROR: invalid operands for chs (-6 3)Notes:
-
Do not modify
postfix-exec-commandfor this part. Instead, just add two bindings to the listpostfix-arithops. -
The Racket built-in
exptfunction is helpful. -
Use a factorial function (we’ve defined many in class!) to implement
chs.
-
-
(4 points) Extend PostFix by adding the following three commands:
leis likelt, but checks “less than or equal to” rather than “less than”geis likegt, but checks “greater than or equal to” rather than “greater than”andexpects two integers at the top of the stack. It replaces them by 0 if either is 0; otherwise it replaces them by 1.
For example:
> (postfix-run '(postfix 0 4 5 le) '()) 1 > (postfix-run '(postfix 0 5 5 le) '()) 1 > (postfix-run '(postfix 0 5 4 le) '()) 0 > (postfix-run '(postfix 0 4 5 ge) '()) 0 > (postfix-run '(postfix 0 4 4 ge) '()) 1 > (postfix-run '(postfix 0 5 4 ge) '()) 1 > (postfix-run '(postfix 0 0 0 and) '()) 0 > (postfix-run '(postfix 0 0 1 and) '()) 0 > (postfix-run '(postfix 0 1 0 and) '()) 0 > (postfix-run '(postfix 0 0 17 and) '()) 0 > (postfix-run '(postfix 0 17 0 and) '()) 0 > (postfix-run '(postfix 0 1 1 and) '()) 1 > (postfix-run '(postfix 0 1 17 and) '()) 1 > (postfix-run '(postfix 0 17 17 and) '()) 1 > (postfix-run '(postfix 0 17 23 and) '()) 1Notes:
-
Do not modify
postfix-exec-commandfor this part. Instead, just add three bindings to the listpostfix-relops. -
The testing function
(test-5c)will test all ofle,ge, andandin the context of the single PostFix programtest-sorted:(define test-sorted '(postfix 3 ; let's call the arguments a, b, and c, from top down 2 nget le ; is a <= b? 3 nget 3 nget ge ; is c >= b? and ; is a <= b and c >= b? )) > (test-5c) ; Uses the test-sorted program in its definition Trying test-sorted on (4 5 6): works as expected; result = 1 Trying test-sorted on (4 5 5): works as expected; result = 1 Trying test-sorted on (4 4 5): works as expected; result = 1 Trying test-sorted on (4 4 4): works as expected; result = 1 Trying test-sorted on (4 6 5): works as expected; result = 0 Trying test-sorted on (5 6 4): works as expected; result = 0 Trying test-sorted on (5 4 6): works as expected; result = 0 Trying test-sorted on (6 5 4): works as expected; result = 0 Trying test-sorted on (6 4 5): works as expected; result = 0 Trying test-sorted on (5 5 4): works as expected; result = 0 Trying test-sorted on (5 4 4): works as expected; result = 0
-
(3 points) Extend PostFix with a
dupcommand that duplicates the top element of the stack (which can be either an integer or executable sequence). For example:(define sos-dup '(postfix 2 dup mul swap dup mul add)) > (postfix-run sos-dup '(3 4)) About to execute commands (dup mul swap dup mul add) on stack (3 4) after executing dup, stack is (3 3 4) after executing mul, stack is (9 4) after executing swap, stack is (4 9) after executing dup, stack is (4 4 9) after executing mul, stack is (16 9) after executing add, stack is (25) 25 (define cmd-dup '(postfix 1 (dup dup mul add swap) dup 3 nget swap exec exec pop)) > (postfix-run cmd-dup '(4)) About to execute commands ((dup dup mul add swap) dup 3 nget swap exec exec pop) on stack (4) after executing (dup dup mul add swap), stack is ((dup dup mul add swap) 4) after executing dup, stack is ((dup dup mul add swap) (dup dup mul add swap) 4) after executing 3, stack is (3 (dup dup mul add swap) (dup dup mul add swap) 4) after executing nget, stack is (4 (dup dup mul add swap) (dup dup mul add swap) 4) after executing swap, stack is ((dup dup mul add swap) 4 (dup dup mul add swap) 4) About to execute commands (dup dup mul add swap) on stack (4 (dup dup mul add swap) 4) after executing dup, stack is (4 4 (dup dup mul add swap) 4) after executing dup, stack is (4 4 4 (dup dup mul add swap) 4) after executing mul, stack is (16 4 (dup dup mul add swap) 4) after executing add, stack is (20 (dup dup mul add swap) 4) after executing swap, stack is ((dup dup mul add swap) 20 4) after executing exec, stack is ((dup dup mul add swap) 20 4) About to execute commands (dup dup mul add swap) on stack (20 4) after executing dup, stack is (20 20 4) after executing dup, stack is (20 20 20 4) after executing mul, stack is (400 20 4) after executing add, stack is (420 4) after executing swap, stack is (4 420) after executing exec, stack is (4 420) after executing pop, stack is (420) 420 > (postfix-run '(postfix 0 dup) '()) ERROR: dup requires a nonempty stack ()Notes:
-
Implement
dupby adding acondclause topostfix-exec-command. -
Test your
dupimplementation using the above test cases. Yourdupimplementation should ensure there is at least one value on the stack, and give an appropriate error message when there isn’t.
-
-
(10 points) In this part you will extend PostFix with a
rotcommand that behaves as follows. The top stack value should be a positive integer rotlen that we’ll call the rotation length. Assume there are n values v1, …, vn below rotlen on the stack, where n is greater than or equal to rotlen. Then the result of performing therotcommand is to rotate the top rotlen elements of the stack by moving v1 after vrotlen. I.e., the order of values on the stack afterrotshould be v2, …, vrotlen, v1, vrotlen+1, …, vn. So the first rotlen elements of the stack have been rotated by one unit, while the order of the remaining elements on the stack is unchanged.Here are examples involving
rot:(define rot-test '(postfix 6 4 rot 3 rot 2 rot)) > (postfix-run rot-test '(8 7 6 5 9 10)) About to execute commands (4 rot 3 rot 2 rot) on stack (8 7 6 5 9 10) after executing 4, stack is (4 8 7 6 5 9 10) after executing rot, stack is (7 6 5 8 9 10) after executing 3, stack is (3 7 6 5 8 9 10) after executing rot, stack is (6 5 7 8 9 10) after executing 2, stack is (2 6 5 7 8 9 10) after executing rot, stack is (5 6 7 8 9 10) 5 > (postfix-run '(postfix 3 (mul add) rot) '(5 6 7)) About to execute commands ((mul add) rot) on stack (5 6 7) after executing (mul add), stack is ((mul add) 5 6 7) ERROR: rot length must be a positive integer but is (mul add) > (postfix-run '(postfix 3 -1 rot) '(5 6 7)) About to execute commands (-1 rot) on stack (5 6 7) after executing -1, stack is (-1 5 6 7) ERROR: rot length must be a positive integer but is -1 > (postfix-run '(postfix 3 4 rot) '(5 6 7)) About to execute commands (4 rot) on stack (5 6 7) after executing 4, stack is (4 5 6 7) ERROR: not enough stack values for rot (4 5 6 7) > (postfix-run '(postfix 0 rot) '()) About to execute commands (rot) on stack () ERROR: rot requires a nonempty stack but is ()Notes:
-
Implement
rotby adding acondclause topostfix-exec-command. -
Racket supplies a
list-tailfunction that is very helpful for implementingrot:> (list-tail '(10 20 30 40 50) 0) '(10 20 30 40 50) > (list-tail '(10 20 30 40 50) 1) '(20 30 40 50) > (list-tail '(10 20 30 40 50) 2) '(30 40 50) > (list-tail '(10 20 30 40 50) 3) '(40 50) > (list-tail '(10 20 30 40 50) 4) '(50) > (list-tail '(10 20 30 40 50) 5) '()Racket does not provide a similar
list-headfunction, but I have provided it in theps6-postfix-starter.rktfile. It works this way:> (list-head '(10 20 30 40 50) 0) '() > (list-head '(10 20 30 40 50) 1) '(10) > (list-head '(10 20 30 40 50) 2) '(10 20) > (list-head '(10 20 30 40 50) 3) '(10 20 30) > (list-head '(10 20 30 40 50) 4) '(10 20 30 40) > (list-head '(10 20 30 40 50) 5) '(10 20 30 40 50) -
Test your
rotimplementation using the above test cases. Yourrotimplementation should give appropriate error messages in various situations, like those in the test cases.
-
Extra Credit: Church Numerals (25 points)
This problem is optional. You should only attempt it after completing all the other problems
The curried n-fold operator cn-fold, defined below has some interesting properties.
(define cn-fold (curry n-fold))
(define twice (cn-fold 2))
(define thrice (cn-fold 3))
(define (add1 y) (+ y 1))
(define (dbl z) (* z 2))
> ((twice add1) 0)
2
> ((thrice add1) 0)
3
> ((twice dbl) 1)
4
> ((thrice dbl) 1)
8In Church’s λ-calculus, it turns out that a function equivalent to (cn-fold n) can be used to represent the nonnegative integer n. As you will see below, you can even do arithmetic on these representations! In fact, these representations are called Church numerals for this reason.
-
(10 points) In the following questions suppose that
aandbare nonnegative integers andfis a unary function. Justify your answer to each question.(1)
(o (n-fold a f) (n-fold b f))is equivalent to(n-fold p f)for what numberp?(2)
(o (cn-fold a) (cn-fold b))is equivalent to(cn-fold q)for what numberq?(3)
((cn-fold a) (cn-fold b))is equivalent to(cn-fold r)for what numberr? -
(5 points) Define a function
incthat takes as its argument a Church numeral fornand returns the Church numeral forn+1. That is, for anyn,(inc (cn-fold n))should return a Church numeral equivalent to(cn-fold (+ n 1)). You are not allowed to use Racket integers or arithmetic on integers in your definition ofinc. For example, it would be easy to defineincas(define (inc churchNum) (cn-fold (+ 1 ((churchNum (lambda (x) (+ x 1))) 0))))but this kind of definition is prohibited.
-
(10 points) Define a function
decthat takes as its argument a Church numeral fornand returns the Church numeral forn-1; in the special case wherenis0, it should return the Church numeral for0. As in the previous part, you are not allowed to use Racket integers or arithmetic on integers in your definition ofdec.
Extra Credit: PostFix Iterations (20 points)
This problem is optional. You should only attempt it after completing all the other problems.
-
(5 points) Study and test the following
mysteryPostFix program of one argument, which is provided near the end ofps6-postfix-starter.rkt. Describe the function that it calculates on its one argument, and give a brief, high-level description of how it calculates that function.;; What function does this compute? (define mystery '(postfix 1 1 (swap dup 0 eq (swap) (swap 2 nget mul swap 1 sub swap 3 vget exec) sel exec) 3 rot 3 vget exec))Note:
vgetis a command that is likenget, except that it can return any value (including an executable sequence), not just an integer. It has been included in yourps6-postfix-starter.rktfile for use in this extra credit problem. -
(15 points) Write a PostFix program that takes a single argument (assumed to be a nonnegative integer n) and iteratively calculates the nth Fibonacci number.