PS8: Set Yourself Free
- Due: Fri. Apr. 20, 2018
- Notes:
- This pset has 100 total points.
- This pset contains one solo problems worth 24 points.
- It is strongly recommended that you do the non-solo SML problems (Problems 3 and 4) first, to get more practice with SML and modules/abstract datatypes that will be valuable going forward.
- The second problem involves reading parts of a long paper. It is best to spread this problem out over multiple sittings.
- Submission:
- In your yourFullName CS251 Spring 2018 Folder, create a Google Doc named yourFullName CS251 PS8.
- At the top of your yourFullName CS251 PS8 doc, include your name, problem set number, date of submission, and an approximation of how long each problem part took.
- For all parts of all problems, include all answers (including SML code) in your PS8 google doc. Format code using a fixed-width font, like Consolas or Courier New. You can use a small font size if that helps.
- For Problem 2 (Backus paper): Include English answers to parts a through f and the alebraic derivation from part g in your Google Doc.
- In Problems 1, 3, and 4, you will create the following code files from starter files populating your
~wx/cs251/sml/ps8directory on your wx Virtual Machine:- Problem 1:
yourAccountName-partialReverses.sml - Problem 3:
yourAccountName-FunSet.sml - Problem 4:
yourAccountName-OperationTreeSet.sml
For these problems:
- include all functions from the three files named
yourAccountName...in your Google Doc (so that I can comment on them). - For Problem 3b, don’t forget to include your English answers in your Google Doc.
-
Drop a copy of your
~wx/cs251/sml/ps8folder in your~/cs251/drop/ps08drop folder oncs.wellesley.eduby executing the following (replacinggdomeby your cs server username):scp -r ~wx/cs251/sml/ps8 gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps08
- Problem 1:
Starting this Problem Set
Problems 1, 3, and 4 involve starter files in the ~wx/cs251/sml/ps8 directory in your wx Virtual Machine.
To create this directory, execute the following four commands in a wx terminal shell:
cd ~/cs251/sml
git add -A
git commit -m "my local changes"
git pull origin master --rebaseIf you encounter any problems when executing these steps, please contact Lyn.
1. Solo Problem: Partial Reverses (24 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
-
(5 points) Consider the following
partial-reversesfunction in Racket. Draw a box-and-pointer diagram of the list that results from the invocation(partial-reverses '(1 2 3 4)). Use the style of diagram shown in PS3 Problem 2. Study the code carefully and be sure to accurately show all sharing between cons cells in your diagram.(define (partial-reverses xs) (define (partial-reverses-tail ys rev list-rev) (if (null? ys) (cons rev list-rev) (partial-reverses-tail (rest ys) (cons (first ys) rev) (cons rev list-rev) ))) (partial-reverses-tail xs '() '()))Note: As an example of sharing in box-and-pointer diagrams, consider
(define numList '(7 2 4)) (define listOfNumLists (list (append numList (rest numList)) numList (rest numList)))The result has 9 cons cells arranged as follows:
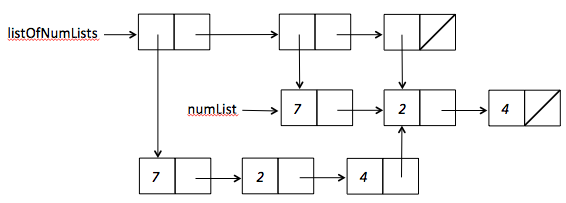
However, if we just enter the printed representation
'((7 2 4 2 4) (7 2 4) (2 4))forlistOfNumLists, that would create 13 cons cells: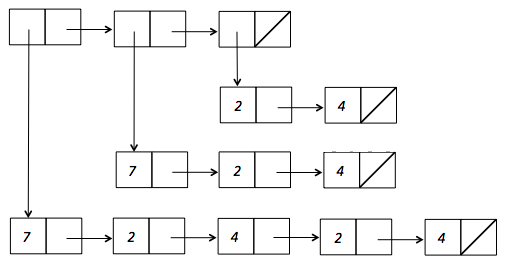
-
(2 points) How many cons cells would there be in the result of
(partial-reverses (range 1 1001))? -
(6 points) Make a copy of the starter file
partialReverses.smlnamedyourAccountName-partialReverses.sml. InyourAccountName-partialReverses.sml, translate the Racket definition ofpartial-reversesinto an SML functionpartialReversesthat has exactly the same behavior (in terms of generating lists with the same sharing).Similar to the
partial-reversesfunction in Racket, the SMLpartialReversesfunction should have a nested function definitionpartialReversesTailthat is called within it.As in PS7 Problems 2 and 3, in this and the following subproblems of this solo task, do not use
#1,#2, etc. to extract tuple components orList.hd,List.tl, orList.nullto decompose and test lists. Instead, use pattern matching on tuples and lists. -
(6 points) In
yourAccountName-partialReverses.sml, flesh out the following SML skeleton definition ofpartialReversesIterateso that it usesiterateto iteratively calculate the same result (including sharing) aspartialReverses:fun partialReversesIterate xs = iterate (* expression1 *) (* expression2 *) (* expression3 *) (xs, [], [])yourAccountName-partialReverses.smlincludes this definition ofiterate(from PS7 Problem 2b):(* val iterate = fn : ('a -> 'a) -> ('a -> bool) -> ('a -> 'b) -> 'a -> 'b *) fun iterate next isDone finalize state = if isDone state then finalize state else iterate next isDone finalize (next state)Notes:
-
In
yourAccountName-partialReverses.sml, the definition ofiteratemust appear above the defintion ofpartialReversesIterate, which uses it. -
You can use
= []to test for an empty list.
-
-
(5 Points) In
yourAccountName-partialReverses.sml, flesh out the following skeleton definition ofpartialReversesFoldlso that it usesfoldlto iteratively calculate the same result (including sharing) aspartialReverses:fun partialReversesFoldl xs = foldl (* expression1 *) (* expression1 *) xsRecall that SML’s
foldlfunction has type('a * 'b -> 'b) -> 'b -> 'a list -> 'b.
2. Backus’s Paper (26 points)
This problem is about John Backus’s 1977 Turing Award Lecture: Can Programming be Liberated from the von Neumann Style? A Functional Style and its Algebra of Programs. His paper can be found here.
You should begin this problem by reading Sections 1–11 and 15–16 of this paper. (Although Sections 12–14 are very interesting, they require more time than I want you to spend on this problem.)
Section 11.2 introduces the details of the FP language. Backus uses many notations that may be unfamiliar to you. For example:
-
p1 → e1; … ; pn → en; en+1 is similar to the Racket expression
(ifp1e1…(ifpnenen+1)…). -
⟨e1, …, en⟩ denotes the sequence of the n values of the expressions e1, … en. φ denotes the empty sequence. Because FP is dynamically typed, such sequences can represent both tuples and lists from Python and OCaml.
-
The symbol ⊥ (pronounced “bottom”) denotes the value of an expression that doesn’t terminate (i.e., it loops infinitely) or terminates with an error.
-
If f is a function and x is an object (atom or sequence of objects), then f : x denotes the result of applying f to x.
-
[f1, …, fn] is a functional form denoting a sequence of n functions, f1 through fn. The application rule for this functional form is [f1, …, fn] : x = ⟨f1 : x, … , fn : x⟩ — i.e., the result of applying a sequence of n functions to an object x is an n-element sequence consisting of the results of applying each of the functions in the function sequence to x.
Consult Lyn if you have trouble understanding Backus’s notation.
Answer the following questions about Backus’s paper. Your answers should be concise but informative.
-
(3 points) One of the reasons this paper is well-known is that in it Backus coined the term “von Neumann bottleneck”. Describe what this is and its relevance to the paper.
-
(3 points) Many programming languages have at least two syntactic categories: expressions and statements. Backus claims that expressions are good but statements are bad. Explain his claim.
-
(3 points) In Sections 6, 7, and 9 of the paper, Backus discusses three problems/defects with von Neumann languages. Summarize them.
-
(3 points) What are applicative languages and how do they address the three problems/defects mentioned by Backus for von Neumann languages?
-
(2 points) The FP language Backus introduces in Section 11 does not support abstraction expressions like Racket’s
lambda. Why did Backus make this decision in FP? -
(2 points) Backus wrote this paper long before the development of Java and Python. Based on his paper, how do you think he would evaluate these two languages?
-
(10 points) Consider the following FP definition:
Def F ≡ α/+ ◦ αα× ◦ αdistl ◦ distr ◦ [id, id]What is the value of F⟨2, 3, 5⟩? Show the evaluation of this expression in a sequence of small-step algebra-like steps.
3. Fun Sets (22 points)
In SML, we can implement abstract data types in terms of familiar structures like lists and trees. But we can also use functions to implement data types. In this problem, you will investigate a compelling example of using functions to implement sets.
Your ~wx/cs251/sml/ps8 folder contains the starter file FunSet.sml. This includes the same SET signature we studied in class:
signature SET =
sig
(* The type of sets *)
type ''a t
(* An empty set *)
val empty : ''a t
(* Construct a single-element set from that element. *)
val singleton : ''a -> ''a t
(* Check if a set is empty. *)
val isEmpty : ''a t -> bool
(* Return the number of elements in the set. *)
val size : ''a t -> int
(* Check if a given element is a member of the given set. *)
val member : ''a -> ''a t -> bool
(* Construct a set containing the given element and all elements
of the given set. *)
val insert : ''a -> ''a t -> ''a t
(* Construct a set containing all elements of the given set
except for the given element. *)
val delete : ''a -> ''a t -> ''a t
(* Construct the union of two sets. *)
val union : ''a t -> ''a t -> ''a t
(* Construct the intersection of two sets. *)
val intersection : ''a t -> ''a t -> ''a t
(* Construct the difference of two sets
(all elements in the first set but not in the second.) *)
val difference : ''a t -> ''a t -> ''a t
(* Construct a set from a list of elements.
Do not assume the list elements are unique. *)
val fromList : ''a list -> ''a t
(* Convert a set to a list without duplicates.
The elements in the resulting list may be in any order. *)
val toList : ''a t -> ''a list
(* Construct a set from a predicate function:
the resulting set should contain all elements for which
this predicate function returns true.
This acts like math notation for sets. For example:
{ x | x mod 3 = 0 }
would be written:
fromPred (fn x => x mod 3 = 0)
*)
val fromPred : (''a -> bool) -> ''a t
(* Convert a set to a predicate function. *)
val toPred : ''a t -> ''a -> bool
(* Convert a set to a string representation, given a function
that converts a set element into a string representation. *)
val toString : (''a -> string) -> ''a t -> string
(* Convert a set to a list without duplicates.
The elements in the resulting list may be in any order. *)
val toList : ''a t -> ''a list
(* Construct a set from a predicate function:
the resulting set should contain all elements for which
this predicate function returns true.
This acts like math notation for sets. For example:
{ x | x mod 3 = 0 }
would be written:
fromPred (fn x => x mod 3 = 0)
*)
val fromPred : (''a -> bool) -> ''a t
(* Convert a set to a predicate function. *)
val toPred : ''a t -> ''a -> bool
(* Convert a set to a string representation, given a function
that converts a set element into a string representation. *)
val toString : (''a -> string) -> ''a t -> string
endBegin this problem by making a copy of FunSet.sml named yourAccountName-FunSet.sml. Make all your edits to yourAccountName-FunSet.sml and not to FunSet.sml.
exception Unimplemented (* Placeholder during development. *)
exception Unimplementable (* Impossible to implement *)
(* Implement a SET ADT using predicates to represent sets. *)
structure FunSet :> SET = struct
(* Sets are represented by predicates. *)
type ''a t = ''a -> bool
(* The empty set is a predicate that always returns false. *)
val empty = fn _ => false
(* The singleton set is a predicate that returns true for exactly one element *)
fun singleton x = fn y => x=y
(* Determining membership is trivial with a predicate *)
fun member x pred = pred x
(* complete this structure by replacing "raise Unimplemented"
with implementations of each function. Many of the functions
*cannot* be implemented; for those, use raise Unimplementable
as there implementation *)
fun isEmpty _ = raise Unimplemented
fun size _ = raise Unimplemented
fun member _ = raise Unimplemented
fun insert _ = raise Unimplemented
fun delete _ = raise Unimplemented
fun union _ = raise Unimplemented
fun intersection _ = raise Unimplemented
fun difference _ = raise Unimplemented
fun fromList _ = raise Unimplemented
fun toList _ = raise Unimplemented
fun fromPred _ = raise Unimplemented
fun toPred _ = raise Unimplemented
fun toString _ = raise Unimplemented
endThe fromPred and toPred operations are based on the observation that a membership predicate describes exactly which elements are in the set and which are not. Consider the following example:
- val s235 = fromPred (fn x => (x = 2) orelse (x = 3) orelse (x = 5));
val s235 = - : int t
- member 2 s235;
val it = true : bool
- member 3 s235;
val it = true : bool
- member 5 s235;
val it = true : bool
- member 4 s235;
val it = false : bool
- member 100 s235;
val it = false : boolThe set s235 consists of exactly those elements satisfying the predicate passed to fromPred – in this case, the integers 2, 3, and 5.
Defining sets in terms of predicates has many benefits. Most important, it is easy to specify sets that have infinite numbers of elements! For example, the set of all even integers can be expressed as:
fromPred (fn x => (x mod 2) = 0)This predicate is true of even integers, but is false for all other integers. The set of all values of a given type is expressed as fromPred (fn x => true). Many large finite sets are also easy to specify. For example, the set of all integers between 251 and 6821 (inclusive) can be expressed as
fromPred (fn x => (x >= 251) && (x <= 6821))Although defining sets in terms of membership predicates is elegant and has many benefits, it has some big downsides. The biggest one is that several functions in the SET signature simply cannot be implemented. You will explore this downside in this problem.
-
(18 points) Flesh out the code skeleton for the
FunSetstructure inyourAccountName-FunSet.sml. Some value bindings cannot be implemented; for these, useraise Unimplementableas the implementation.At the end of the starter file are the following commented out test cases. Uncomment these test cases to test your implementation. Feel free to add additional tests.
open FunSet (* range helper function *) fun range lo hi = if lo >= hi then [] else lo::(range (lo + 1) hi) (* Test an int pred set on numbers from 0 to 100, inclusive *) fun intPredSetToList predSet = List.filter (toPred predSet) (range 0 101) val mod2Set = fromPred (fn x => x mod 2 = 0) val mod3Set = fromPred (fn x => x mod 3 = 0) val lowSet = fromList (range 0 61) val highSet = fromList (range 40 101) val smallSet = insert 17 (insert 19 (insert 23 (singleton 42))) val smallerSet = delete 23 (delete 19 (delete 57 smallSet)) (* Be sure to print all details *) val _ = Control.Print.printLength := 101; val smallSetTest = intPredSetToList(smallSet) val smallerSetTest = intPredSetToList(smallerSet) val mod3SetTest = intPredSetToList(mod3Set) val mod2SetUnionMod3SetTest = intPredSetToList(union mod2Set mod3Set) val mod2SetIntersectionMod3SetTest = intPredSetToList(intersection mod2Set mod3Set) val mod2SetDifferenceMod3SetTest = intPredSetToList(difference mod2Set mod3Set) val mod3SetDifferenceMod2SetTest = intPredSetToList(difference mod3Set mod2Set) val bigIntersection = intPredSetToList(intersection (intersection lowSet highSet) (intersection mod2Set mod3Set)) val bigDifference = intPredSetToList(difference (difference lowSet highSet) (difference mod2Set mod3Set))For the test expressions generating lists, the results are as follows:
val smallSetTest = [17,19,23,42] : int list val smallerSetTest = [17,42] : int list val mod3SetTest = [0,3,6,9,12,15,18,21,24,27,30,33,36,39,42,45,48,51,54,57,60,63,66,69,72,75, 78,81,84,87,90,93,96,99] : int list val mod2SetUnionMod3SetTest = [0,2,3,4,6,8,9,10,12,14,15,16,18,20,21,22,24,26,27,28,30,32,33,34,36,38,39, 40,42,44,45,46,48,50,51,52,54,56,57,58,60,62,63,64,66,68,69,70,72,74,75,76, 78,80,81,82,84,86,87,88,90,92,93,94,96,98,99,100] : int list val mod2SetIntersectionMod3SetTest = [0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96] : int list val mod2SetDifferenceMod3SetTest = [2,4,8,10,14,16,20,22,26,28,32,34,38,40,44,46,50,52,56,58,62,64,68,70,74,76, 80,82,86,88,92,94,98,100] : int list val mod3SetDifferenceMod2SetTest = [3,9,15,21,27,33,39,45,51,57,63,69,75,81,87,93,99] : int list val bigIntersection = [42,48,54,60] : int list val bigDifference = [0,1,3,5,6,7,9,11,12,13,15,17,18,19,21,23,24,25,27,29,30,31,33,35,36,37,39] : int list -
(4 points) For each function that you declared being unimplementable, explain in English why it is unimplementable. Give concrete examples where appropriate.
4. Operation Tree Sets (28 points)
A very different way of representing a set as a tree is to remember the structure of the set operations empty, insert, delete, union, intersection, and difference used to create the set. For example, consider the set t created as follows:
val s = (delete 4 (difference (union (union (insert 1 empty)
(insert 4 empty))
(union (insert 7 empty)
(insert 4 empty)))
(intersection (insert 1 empty)
(union (insert 1 empty)
(insert 6 empty)))))Abstractly, s is the singleton set {7}. But one concrete representation of s is the following operation tree:
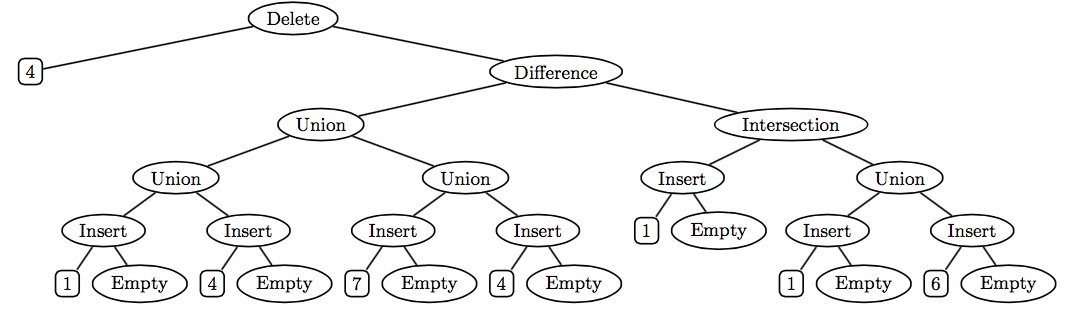
One advantage of using such operation trees to represent sets is that the empty, insert, delete, union, difference, and intersection operations are extremely cheap — they just create a new tree node with the operands as subtrees, and thus take constant time and space! But other operations, such as member and toList, can be more expensive than in other implementations.
In this problem, you are asked to flesh out the missing operations in the skeleton of the OperationTreeSet structure shown below. Your ~wx/cs251/sml/ps8 folder contains the starter file OperationTreeSet.sml.
Begin this problem by making a copy of OperationTreeSet.sml named yourAccountName-OperationTreeSet.sml. Make all your edits to yourAccountName-OperationTreeSet.sml and not to OperationTreeSet.sml.
structure OperationTreeSet :> SET = struct
datatype ''a t = Empty
| Insert of ''a * ''a t
| Delete of ''a * ''a t
| Union of ''a t * ''a t
| Intersection of ''a t * ''a t
| Difference of ''a t * ''a t
val empty = Empty
fun insert x s = Insert(x,s)
fun singleton x = Insert(x, Empty)
fun delete x s = Delete(x, s)
fun union s1 s2 = Union(s1,s2)
fun intersection s1 s2 = Intersection(s1,s2)
fun difference s1 s2 = Difference(s1,s2)
fun member _ _ = raise Unimplemented
fun toList _ = raise Unimplemented
fun isEmpty _ = raise Unimplemented
fun size _ = raise Unimplemented
fun toPred _ = raise Unimplemented
fun toString eltToString _ = raise Unimplemented
fun fromList _ = raise Unimplemented
fun fromPred _ = raise Unimplementable
endIn the OperationTreeSet structure, the set datatype t is create by constructors Empty, Insert, Delete, Union, Intersection, and Difference. The empty, singleton, insert, delete, union, intersection, difference operations are easy and have been implemented for you. You are responsible for fleshing out the definitions of the member, toList, size, isEmpty, toPred, toString, and fromList operations.
Notes:
-
Your implementation of
membershould not use thetoListfunction. Instead, it should be defined by case analysis on the structure of the operation tree. -
For the
toListfunction:-
toListshould also be defined by case analysis on the structure of the operation tree. -
The
memberfunction should not be used in the implementation oftoList(because it can be very inefficient). Instead, useList.existsandList.filterin a manner similar to the way we implemented sets as lists without duplicates in class. -
Keep in mind that sets are unordered. So your
toListfunction may return lists of elements in any order, but it should not have any duplicates. -
In your
toListdefinition, be very careful with includingtoListinside functional arguments, because this can often cause the same list to be calculated a tremendous number of times, leading to tests that take a very long time for large sets. If some of the test cases for large sets don’t return in a reasonable time, this is probably the cause. You can avoid this by using SML’slet/in/endto name the result of calculatingtoListand using the name multiple times.
-
-
Your implementation of
sizeandisEmptyshould use thetoListfunction. Indeed, it is difficult to implement these functions by a direct case analysis on the operation tree. Note thatsizewill only work correcty if the output oftoListdoes not contain duplicates. -
In the implementation of
toString, the functionString.concatWithis particularly useful. -
In the implementation of
fromList, for lists with >= 2 elements, you should first split the list into two (nearly) equal-length sublists usingList.takeandList.dropand union the results of turning the sublists into sets. This yields a height-balanced operation tree. -
yourAccountName-OperationTreeSet.smlends with two collections of test cases. The first collection involves “small” sets that are defined without usingfromList. The second collection involves “big” sets that are defined usingfromList. The expected outputs to these tests can be found in this transcript file. Because of the way the testing functions are written, the integer elements in the outputs formemberandtoPredwill be in sorted order from low to high, but the integers in the outputs fortoListandtoStringmay be in any order. -
The testing code for most functions (all except for
member) assumes thattoListworks correctly. So you must implementtoListfor for most of the tests to work.