PS7: Resistance is Futile. You Will Be SMLated.
 )
)
- Due: Wednesday, April 11, 2018
- Notes:
- This pset has 100 total points:
- It has one solo problems worth 40 points involving an extension of the PostFix interpreter in Racket.
- It has two regular problems worth 60 points on SML programming:
- The first SML problem is based on material from the lectures on Introduction to SML slides w/solutions here and List Processing in SML slides w/solutions here, most of which has been covered in class.
- The second SML problem requires lecture material on sum-of-product (SOP) datatypes [slides w/fill-in-the-blanks here}(http://cs.wellesley.edu/~cs251/slides/sml-sop_4up.pdf), which will be covered after break.
- So that you are better prepared for the SML material in class, it is strongly recommended that you complete the first SML problem before starting the Racket solo problem and start working on the second SML problem after the SOP leture on Tuesday, April 03.
- This pset has 100 total points:
-
Times from Fall ‘17
The following times do not include Solo Problem 1, which is a new problem.
Times Problem 2 Problem 3 Total (Excluding Problem 1) average time (hours) 3.45 3.2 6.65 median time (hours) 3.25 3 6.25 max time (hours) 5.5 6 11.5 - Submission:
- In your yourFullName CS251 Spring 2017 Folder, create a Google Doc named yourFullName CS251 PS7.
- At the top of your yourFullName CS251 PS7 doc, include your name, problem set number, date of submission, and an approximation of how long each problem part took.
- For all parts of all problems, include all answers (including Racket and SML code) in your PS7 Google Doc. Format Racket and SML code using a fixed-width font, like Consolas or Courier New. You can use a small font size if that helps.
- For Problem 1 (the solo problem on PostLoop):
- In your Google Doc include:
- the answers to the questions in Part 1a
- the two iteration tables for Part 1b
- the four PostLoop programs for Part 1c
- your final version of the function
postloop-exec-config-tail, which has your fleshed out implementation of theforcommand. This is the only function from the PostLoop intepreter you should include in your Google Doc.
- Drop a copy of
yourAccountName-ps7-postloop-config-tail-fancy.rktin your~/cs251/drop/ps07drop folder oncs.wellesley.edu.
- In your Google Doc include:
- For Problems 2 and 3:
- Include the SML code from
yourAccountName-ps7-holo.smlin your Google Doc (so that I can comment on it). - Include the SML code from
yourAccountName-TTTreeFuns.smlin your Google Doc (so that I can comment on it). -
Drop a copy of your
~wx/cs251/sml/ps7folder in your~/cs251/drop/ps07drop folder oncs.wellesley.eduby executing the following (replacinggdomeby your cs server username):scp -r ~wx/cs251/sml/ps7 gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps07
- Include the SML code from
1. Solo Problem: PostLoop (40 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
In this problem, you will consider a PostLoop language that extends PostFix.
Begin this problem by downloading the starter file ps7-postloop-config-tail-fancy-starter.rkt, which you should rename to yourAccountName-ps7-postloop-config-tail-fancy.rkt. This .rkt file contains a PostLoop interpreter that handles programs that begin with the keywords postloop and postfix:
-
Programs beginning with
postfixare exactly those described in the PostFix slides (without the extensions described in PS06 =exp,chs,le,ge,and,dup,rot, andvget) -
Programs beginning with
postloopcan use all PostFix commands plus four addition ones:pair,fst,snd, andfor. The implementations of the first three commands are fleshed out in the file. You will flesh out the implementation of theforcommand in this file. Using the different program keywordpostloophighlights which programs can use the four new commands.
-
(6 points) The
pair,fst, andsndcommands manipulate pair values. StudyyourAccountName-ps7-postloop-config-tail-fancy.rktto answer these questions about pair values and these commands:-
The
paircommand creates a pair value. What is the printed representation of this value? -
A pair value has two value components. What are the valid types of values for these components?
-
Show the semantics of each of the three commands
pair,fst, andsndusing the Stack Before/Command/Stack After row notation in the table for PostFix command semantics on slide 4 of the PostFix slides. -
There are three spots in the PostLoop interpreter that allow pair values (not the
paircommand) in addition to integer values where the PostFix interpreter requires integer values. Briefly summarize how these three changes affect three aspects of the high-level semantics of PostLoop relative to PostFix. (Don’t mention any code details, just how the high-level semantics changes.)
-
-
(8 points) The
forcommand is a numerical looping construct for PostLoop. Here is the semantics of theforcommand expressed in two rows of a table that shows how theforcommand changes both the command sequence and stack of a PostFix configuration:Commands Before Stack Before Commands After Stack After (for ...)((C1 ... Cn) 0 ...)(...)(...)(for ...)((C1 ... Cn) N ...)(C1 ... Cn N_dec (C1 ... Cn) for ...)(N ...)The
forcommand expects two arguments on the stack:-
A command sequence
(C1 ... Cn)with n commands (n may be zero). -
An nonnegative integer
N.
The first row of the table says that when
Nis0, theforcommand terminates the loop by popping both arguments off the stack.In the second row of the table, it is assumed that
Nis a positive integer, andN_decis the result of subtracting 1 fromN. In this case, theforcommand will first execute an iteration of the loop by executing the n commandsC1throughCnstarting with a stack in which the command sequence has been popped andNis now at the top. Then it will execute the remaining iterations of the loop when it executesN_dec (C1 ... Cn) for. The looping behavior comes from the fact that for nonzeroN, theforcommand rewrites the commands to a sequence that ends inforon the same command sequence for an integer that is one smaller. The loop continues until the integer becomes 0, at which point the loop terminates.In this part, you will get a better understanding for how the
forcommand works by using the configuration semantics to show the execution of two one-argument PostLoop programs on the argument list(3):postloop-pgm1=(postloop 1 0 2 nget (pair) for)postloop-pgm2=(postloop 1 0 2 nget (swap 10 mul add) for)
For each program, draw an iteration table with the two columns Commands and Stack, where the first row has the initial program command sequence for Commands and
(3)for Stack. Then use the PostLoop semantics to flesh out the remaining rows of the table until the program terminates. -
-
(18 points) In this part, you will define four PostLoop programs that use a single
forloop. Here are some notes that apply to all four functions:-
You needn’t show any iteration tables for these programs, though you may want to draw some while designing them.
-
You should comment your programs to explain what the parts are doing.
-
In
yourAccountName-ps7-postloop-config-tail-fancy.rkt, you should flesh out the definitions (near the bottom of the files) of the variablespostloop-fact,postloop-expt,postloop-pairs-up, andpostloop-fibto be quoted s-expressions of the programs you developed in this part. You will use these programs to test your implementations of theforcommand in Part 1d.
i. (2 points)
postloop-fact: a PostLoop program that takes one argument (assume it’s a nonnegative integer n, no error checking necessary) and returns the factorial of n. Here are examples of the input/output behavior of this program:Args Result (0) 1 (1) 1 (2) 2 (3) 6 (4) 24 (5) 120 ii. (5 points)
postloop-expt: a PostLoop program that takes two arguments (a base and an exponent) and returns the result of raising the base to the exponent. You may assume that that both arguments are integers and the second integer (exponent) is nonnegative (no error-checking necessary). Some examples:Args Result (2 0) 1 (2 1) 2 (2 2) 4 (2 3) 8 (2 4) 16 (2 5) 32 (3 0) 1 (3 1) 3 (3 2) 9 (3 3) 27 (3 4) 81 (3 5) 243 (4 2) 16 (5 3) 125 (-3 3) -27 (-3 4) 81 (-5 3) -243 iii. (5 points)
postloop-pairs-up: a PostLoop program that takes one argument (assume it’s a nonnegative integer n, no error checking necessary) and returns afst-nested sequence of n pairs with numbers going up from 0 to n, as shown below:Args Result (0) 0 (1) (0 . 1) (2) ((0 . 1) . 2) (3) (((0 . 1) . 2) . 3) (4) ((((0 . 1) . 2) . 3) . 4) (5) (((((0 . 1) . 2) . 3) . 4) . 5) iv. (6 points)
postloop-fib: a PostLoop program that takes one argument (assume it’s a nonnegative integer n, no error checking necessary) and returns the Fibonacci of n:Args Result (0) 0 (1) 1 (2) 1 (3) 2 (4) 3 (5) 5 (6) 8 (7) 13 (8) 21 (9) 34 (10) 55 Note: In this problem, it is recommended that you represent the state of the iteration as a pair value with two integers.
-
-
(8 points) In this part, you will flesh out the implementation of the
forcommand inyourAccountName-ps7-postloop-config-tail-fancy.rkt. Do this by replacing the stub for handling theforcommand within thepostloop-exec-config-tailfunction. It should implement the configuration-based semantics explained in Part 1b above. Additionally, it should handle error cases exactly as indicated in the following examples (where[ERROR ICONS]stands for the red error icons displayed by Racket when there’s an error):> (postloop-run '(postloop 0 17 5 (add) for) '()) 32 > (postloop-run '(postloop 0 17 -5 (add) for) '()) [ERRROR ICONS] for requires nonnegative integer as first arg -5 > (postloop-run '(postloop 0 17 (2 add) (3 mul) for) '()) [ERRROR ICONS] for requires nonnegative integer as first arg (2 add) > (postloop-run '(postloop 0 17 (add) 5 for) '()) [ERROR ICONS] for requires nonnegative integer as first arg (add) > (postloop-run '(postloop 0 17 5 3 for) '()) [ERRROR ICONS] for requires command sequence as second arg 3 > (postloop-run '(postloop 0 17 for) '()) [ERRROR ICONS] for requires two arguments (17)Notes:
-
The
.rktfile ends with a commented out expression(test-loops loop-tests). If you uncomment this, then when you run the Racket file, it will test your the interpreter on the PostLoop programspostloop-pgm1,postloop-pgm2,postloop-fact,postloop-expt,postloop-pairs-up, andpostloop-fibon a variety of arguments. It knows the expected results, and will indicate a test failure if the actual result is not equal to the expected one. -
To reduce the amount of printout during testing, the
display-steps?variable has been set to#fby default near the top of the file. But when debugging, you probably want to set this to#t, so that you can see the sequence of configurations for each test case. -
The test cases do not test the error cases mentioned above. You’ll have to test those by hand.
-
2. Higher-order List Operators in SML (30 points)
In this problem, you will revisit several of the higher-order list operators we have studied in Racket in the context of SML. Since you are already familiar with these operators, your focus in this problem is on SML syntax and type-checking, rather than on the operators themselves.
-
range,digitsToDecimal,cartesianProduct,partition(10 points). Translate the following Racket functionsrange,digits->decimal,cartesian-product, andpartitioninto corresponding SML functions namedrange,digitsToDecimal,cartesianProduct, andpartitionfunctions:(define (range lo hi) (if (<= hi lo) null (cons lo (range (+ 1 lo) hi)))) (define (digits->decimal digits) (foldl (λ (digit sum) (+ (* 10 sum) digit)) 0 digits)) (define (cartesian-product xs ys) (foldr (λ (x subres) (append (map (λ (y) (cons x y)) ys) subres)) null xs)) (define (partition pred xs) (foldr (λ (x two-lists) (if (pred x) (list (cons x (first two-lists)) (second two-lists)) (list (first two-lists) (cons x (second two-lists))))) (list '() '()) xs))For example:
val range = fn : int -> int -> int list val digitsToDecimal = fn : int list -> int val cartesianProduct = fn : 'a list -> 'b list -> ('a * 'b) list val partition = fn : ('a -> bool) -> 'a list -> 'a list * 'a list - range 0 10; val it = [0,1,2,3,4,5,6,7,8,9] : int list - range 3 8; val it = [3,4,5,6,7] : int list - range 5 5; val it = [] : int list - range 1 100; val it = [1,2,3,4,5,6,7,8,9,10,11,12,...] : int list - Control.Print.printLength := 100; - val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28, 29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53, 54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78, 79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99] : int list - digitsToDecimal [2, 5, 1] val it = 251 : int - digitsToDecimal [1, 7, 2, 9] val it = 1729 : int - digitsToDecimal (range 0 10); val it = 123456789 : int - digitsToDecimal [] val it = 0 : int - cartesianProduct [1,2,3,4] ["a", "b", "c"]; val it = [(1,"a"),(1,"b"),(1,"c"),(2,"a"),(2,"b"),(2,"c"),(3,"a"),(3,"b"),(3,"c"), (4,"a"),(4,"b"),(4,"c")] : (int * string) list - cartesianProduct ["a", "b", "c"] [1,2,3,4]; val it = [("a",1),("a",2),("a",3),("a",4),("b",1),("b",2),("b",3),("b",4),("c",1), ("c",2),("c",3),("c",4)] : (string * int) list - partition (fn x => x mod 2 = 0) [4, 2, 7, 8, 5, 1, 9, 3, 6]; val it = ([4,2,8,6],[7,5,1,9,3]) : int list * int list - partition (fn x => x < 4) [4, 2, 7, 8, 5, 1, 9, 3, 6]; val it = ([2,1,3],[4,7,8,5,9,6]) : int list * int list - partition (fn x => x > 0) [4, 2, 7, 8, 5, 1, 9, 3, 6]; val it = ([4,2,7,8,5,1,9,3,6],[]) : int list * int listNotes: (Read ALL of these notes before proceeding with Problem 2a!)
-
You should do all your SML programming in Emacs within the
wxvirtual machine appliance or ontempest=cs.wellesley.edu. (If you wish to usetempest, contact Lyn about setting up the CS251 git repository in yourtempestaccount.) -
It is strongly recommended that you learn (or review) Emacs, especially the keyboard shortcuts, before continuing with this problem. Start by taking the Emacs tutorial, which you can run in Emacs via
C-h torM-x help-with-tutorial, then review these Emacs notes. -
You should also have the GNU Emacs Reference Card handed out by your side when using Emacs to help you learn keyboard commands.
-
Review slides 19-20 from the Introduction to SML lecture on running SML in Emacs. Also read these notes on SML/NJ and Emacs SML Mode and follow the advice there. In particular, it is strongly recommended that you create an SML interpreter within a
*sml*buffer in Emacs. Then you can useM-pandM-nto avoid retyping your test expressions. -
In this and the following parts of this problem, write all of your SML code in a new file named
yourAccountName-ps7-holo.smlthat is within the~wx/cs251/sml/ps7folder on your wx virtual machine. In particular, your workflow should be as follows:-
Do not create the
~wx/cs251/sml/ps7folder from scratch. Instead, you should pull it from thegitrepository by executing the following commands in a shell on yourwxVM:cd ~/cs251/sml git pull origin masterWhen beginning a programming session on any particular day, it is wise to begin with this pull so that you have the most recent version of all CS251 SML files.
-
Create a new file
~wx/cs251/sml/ps7/yourAccountName-ps7-holo.smlin Emacs by using theC-x C-fkeyboard shortcut or the menu itemFile>Visit New File. -
Every time you change the file
yourAccountName-ps7-holo.smland want to test your changes in a*sml*SML interpreter butter, use theC-c C-bkeyboard shortcut (followed by areturnif prompted in the mini-buffer at the bottom of the screen) or the menu itemSML>Process>Send Buffer. You may need to scroll down to the bottom of the*sml*buffer to see what has been loaded. These steps create a new*sml*buffer is created if one does not exist; otherwise, the existing*sml*buffer is reused. (slide 20 of the Introduction to SML lecture indicates thatC-c C-sis necessary to first create the*sml*buffer, but this is not true;C-c C-bwill create it if it doesn’t exist.C-c C-sis useful for opening the*sml*buffer if it is accidentally closed.)
-
-
In all of your SML programming, do not use
#1,#2, etc. to extract tuple components orList.hd,List.tl, orList.nullto decompose and test lists. Instead, use pattern matching on tuples and lists, as illustrated in examples from the SML lectures. (List.tlandList.nullare permissible in rare situations, but#1,#2, andList.hdshould never be used.) -
Because hyphens are not allowed in SML identifiers, you should translate all hyphens in Racket identifiers either to underscores (so-called ``snake case’’) or camel case. E.g.,
cartesian-productin Racket becomescartesian_productorcartesianPrductin SML. Here and below, other name changes are also required due to limitations in SML identifiers; e.g.,->indigits->decimalis converted toTo. -
Liberally and carefully use explicit parentheses for grouping expressions in SML. Many type errors in SML programs come from unparenthesized epxressions that are parsed in ways unexpected by the programmer. In Lyn’s experience, missing or misplaced parens are the most common source of type errors for students learning to program in SML, so always check parens when debugging type errors.
-
foldr,foldl,map, andList.filterare all built into SML:val foldr = fn: ('a * 'b -> 'b) -> 'b -> 'a list -> 'b val foldl = fn: ('a * 'b -> 'b) -> 'b -> 'a list -> 'b val map = fn: ('a -> 'b) -> 'a list -> 'b list - List.filter; val it = fn : ('a -> bool) -> 'a list -> 'a listNote that
List.filterrequires the explicit module prefixList., while the other functions do not. Go figure! -
Racket’s
appendtranslates to SML’s infix@operator, but when you want to pass it as an argument to a first-class function you write it asop@. -
In this entire problem (not just this part) some instances of Racket’s
conswill translate to SML’s infix list-prepending operator::, while others will translate to the tupling notation(<exp1>, <exp2>)for pair creation. Reason about SML types to figure out which to use when. SML’s type checker will yell at you if you get it wrong. -
In this entire problem (not just this part) some instances of Racket’s
listwill translate to SML’s lists while others will translate to SML’s tuples. Again, reason about SML types to figure out which to use when. -
Control.Print.printLengthcontrols how many list elements are displayed; after this number, ellipses are used. For example:- Control.Print.printLength := 5; val it = () : unit - range 0 20; val it = [0,1,2,3,4,...] : int list - Control.Print.printLength := 20; val it = () : unit - range 0 20; val it = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19] : int listAnother such control is
Control.Print.printDepth, which controls printing in nested lists. You won’t need that here, but will in Problem 3.
-
-
allContainMultiple,keepBiggerThanNext,foldrTernop, andkeepBiggerThanSomeFollowing(10 points) Translate the following Racket functionsall-contain-multiple?,keep-bigger-than-next,foldr-ternop, andkeep-bigger-than-some-followinginto corresponding SML functions nameddoAllContainMultple,keepBiggerThanNext,foldrTernop, andkeepBiggerThanSomeFollowing:(define (all-contain-multiple? m nss) (forall? (lambda (ns) (exists? (lambda (n) (divisible-by? n m)) ns)) nss)) (define (keep-bigger-than-next nums) (if (null? nums) '() (map car (filter (λ (pair) (> (car pair) (cdr pair))) (zip nums (rest nums)))))) (define (foldr-ternop ternop nullval xs) (if (null? xs) nullval (ternop (first xs) (rest xs) (foldr-ternop ternop nullval (rest xs))))) (define (keep-bigger-than-some-following nums) (foldr-ternop (λ (fstNum rstNums bigs) (if (exists? (λ (n) (> fstNum n)) rstNums) (cons fstNum bigs) bigs)) '() nums))For example:
val doAllContainMultiple = fn : int -> int list list -> bool val keepBiggerThanNext = fn : int list -> int list val foldrTernop = fn : ('a * 'a list * 'b -> 'b) -> 'b -> 'a list -> 'b val keepBiggerThanSomeFollowing = fn : int list -> int list - doAllContainMultiple 5 [[17,10,2],[25],[3,8,5]]; val it = true : bool - doAllContainMultiple 2 [[17,10,2],[25],[3,8,5]]; val it = false : bool - doAllContainMultiple 3 []; val it = true : bool - keepBiggerThanNext [6, 1, 4, 7, 2, 5, 9, 8, 3]; val it = [6,7,9,8] : int list - keepBiggerThanNext [9,7,8,6,4,5,3,1,2]; val it = [9,8,6,5,3] : int list - keepBiggerThanNext (range 0 20); val it = [] : int list - keepBiggerThanSomeFollowing [6, 1, 4, 7, 2, 5, 9, 8, 3]; val it = [6,4,7,5,9,8] : int list - keepBiggerThanSomeFollowing [9,7,8,6,4,5,3,1,2]; val it = [9,7,8,6,4,5,3] : int list - keepBiggerThanSomeFollowing (range 0 20); val it = [] : int listNotes:
-
SML includes the following analogs of
forall?,exists?, andzipthat you should use in your definitions:- List.all; val it = fn : ('a -> bool) -> 'a list -> bool - List.exists; val it = fn : ('a -> bool) -> 'a list -> bool - ListPair.zip; val it = fn : 'a list * 'b list -> ('a * 'b) list -
Because SML does not allow
?in identifiers, Racket names containing?need to be be transformed, as inall-contain-multiple?todoAllContainMultiple. -
The
List.andListPair.indicate that these functions come from modules. Here is documentation on theListmodule, and here is documentation on theListPairmodule. -
In
keepBiggerThanNextandfoldrTernop, rather than usingList.null numsornums = []to check for an empty list andList.hdandList.tlto extract the parts of a list, you should instead use pattern patching to to distinguish empty and nonempty lists and find the parts of a nonempty list. Here’s a simple example that illustrates such pattern matching:fun mapScale factor [] = [] | mapScale factor (num::nums) = (factor * num) :: (mapScale factor nums)
-
-
genlist,partialSumsTable,iterate, andfibPairs(10 points). Translate the following Racket functionsgenlist-apply,partial-sums-table,iterate-apply, andfib-pairsfunctions into SML functions namdedgenlist,partialSumsTable,iterate, andfibPairs:(define (genlist-apply next done? keepDoneValue? seed) (if (apply done? seed) (if keepDoneValue? (list seed) null) (cons seed (genlist-apply next done? keepDoneValue? (apply next seed))))) (define (partial-sums-table ns) (genlist-apply (λ (nums ans) (list (rest nums) (+ (first nums) ans))) (λ (nums ans) (null? nums)) #t (list ns 0))) (define (iterate-apply next done? finalize state) (if (apply done? state) (apply finalize state) (iterate-apply next done? finalize (apply next state)))) (define (fib-pairs threshold) ;; returns a list of pairs (a, b) used to calculate Fibonacci iteratively ;; until b is greater than or equal to the given threshold (iterate-apply (λ (a b pairs) (list b (+ a b) (cons (cons a b) pairs))) (λ (a b pairs) (>= b threshold)) (λ (a b pairs) (reverse (cons (cons a b) pairs))) '(0 1 ())))For example:
val genlist = fn : ('a -> 'a) -> ('a -> bool) -> bool -> 'a -> 'a list val partialSumsTable = fn : int list -> (int list * int) list val iterate = fn : ('a -> 'a) -> ('a -> bool) -> ('a -> 'b) -> 'a -> 'b val fibPairs = fn : int -> (int * int) list - genlist (fn n => n * 2) (fn n => n > 1000) true 1; val it = [1,2,4,8,16,32,64,128,256,512,1024] : int list - genlist (fn n => n * 2) (fn n => n > 1000) false 1; val it = [1,2,4,8,16,32,64,128,256,512] : int list - partialSumsTable [7, 2, 5, 8, 4]; val it = [([7,2,5,8,4],0),([2,5,8,4],7),([5,8,4],9),([8,4],14),([4],22),([],26)] : (int list * int) list - partialSumsTable (range 1 11); val it = [([1,2,3,4,5,6,7,8,9,10],0),([2,3,4,5,6,7,8,9,10],1),([3,4,5,6,7,8,9,10],3), ([4,5,6,7,8,9,10],6),([5,6,7,8,9,10],10),([6,7,8,9,10],15),([7,8,9,10],21), ([8,9,10],28),([9,10],36),([10],45),([],55)] : (int list * int) list (* Return the first sum of powers of 3 that's greater than 100 *) - iterate (fn (power, sum) => (3*power, power+sum)) = (fn (power, sum) => sum > 100) = (fn (power, sum) => sum) = (1, 0); val it = 121 : int (* = 1 + 3 + 9 + 27 + 81 *) - fibPairs 10; val it = [(0,1),(1,1),(1,2),(2,3),(3,5),(5,8),(8,13)] : (int * int) list - fibPairs 50; val it = [(0,1),(1,1),(1,2),(2,3),(3,5),(5,8),(8,13),(13,21),(21,34),(34,55)] : (int * int) list - fibPairs 100; val it = [(0,1),(1,1),(1,2),(2,3),(3,5),(5,8),(8,13),(13,21),(21,34),(34,55),(55,89), (89,144)] : (int * int) listNotes:
-
SML does not allow
?in identifiers, so translatedone?tois_doneorisDoneand similarly withkeepDoneValue? -
Use pattern matching on tuples when translating the
(λ (nums ans) ...)and(λ (a b pairs) ...)functions; you should not use#1,#2, or#3in any of your definitions. Translate these to(fn (nums,ans) => ...)and(fn (a,b,pairs) => ...). Because of SML’s built-in pattern matching, in SML it is unnecessary to have a separate function like Racket’sgenlist-applyanditerate-apply(as distinct fromgenlistanditerate) in SML since the function arguments in SML’sgenlistanditeratecan already do pattern matching.
-
3. 2-3 Trees (30 points)
In this problem you will use SML to implement aspects of 2-3 trees, a particular search tree data structure that is guaranteed to be balanced.
Begin by skimming pages 1 through 7 of this handout on 2-3 trees. (I created this handout for CS230 in Fall, 2004, but we no longer teach 2-3 trees in that course).
In a 2-3 tree, there are three kinds of nodes: leaves, 2-nodes, and 3-nodes. Together, these can be expressed in SML as follows:
datatype TTTree = (* 2-3 tree of ints *)
L (* Leaf *)
| W of TTTree * int * TTTree (* tWo node *)
| H of TTTree * int * TTTree * int * TTTree (* tHree node *)For simplicity, we will only consider 2-3 trees of integers, though they can be generalized to handle any type of value.
For conciseness in constructing and displaying large trees, the three constructors have single-letter names. For example, below are the pictures of four sample 2-3 trees from the handout and how they would be expressed with these constructors:
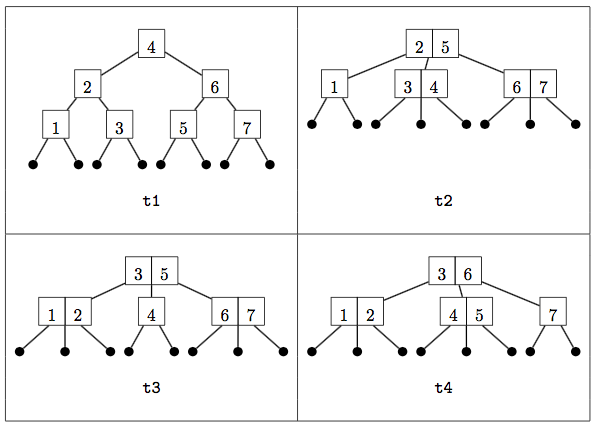
val t1 = W( W(W(L,1,L), 2, W(L,3,L)), 4, W(W(L,5,L), 6, W(L,7,L)))
val t2 = H( W(L,1,L), 2, H(L,3,L,4,L), 5, H(L,6,L,7,L))
val t3 = H( H(L,1,L,2,L), 3, W(L,4,L), 5, H(L,6,L,7,L))
val t4 = H( H(L,1,L,2,L), 3, H(L,4,L,5,L), 6, W(L,7,L))As explained in the handout on 2-3 trees, a 2-3 tree is only valid it it satisfies two additional properties:
- The ordering property:
- In a 2-node with left subtree l, value X, and right subtree r, (all values in l) ≤ X ≤ (all values in r).
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, (all values in l) ≤ X ≤ (all values in m) ≤ Y ≤ (all values in r).
- The height property (called path length invariant in the handout): in a 2-node or 3-node, the height of all subtrees must be exactly the same.
The height property guarantees that a valid 2-3 tree is balanced. Together, these two properties guarantee that a 2-3 tree is efficiently searchable.
Your ~wx/cs251/sml/ps7 folder includes the file TTTree.sml, which contains the TTTree dataytype defined above as well as numerous examples of valid and invalid 2-3 trees that are instances of this datatype. Note that t and vt are used for valid trees, io is used for invalidly ordered trees, and ih is used for invalid height trees.
| tree name | elements | ordered? | satisfies the height property? |
|---|---|---|---|
| t1 | [1,…,7] | Yes | Yes, with height 3 |
| t2 | [1,…,7] | Yes | Yes, with height 2 |
| t3 | [1,…,7] | Yes | Yes, with height 2 |
| t4 | [1,…,7] | Yes | Yes, with height 2 |
| vt0 | [] | Yes | Yes, with height 0 |
| vt2 | [1,2] | Yes | Yes, with height 1 |
| vt17 | [1,…,17] | Yes | Yes, with height 3 |
| vt20 | [1,…,20] | Yes | Yes, with height 4 |
| vt44 | [1,…,44] | Yes | Yes, with height 5 |
| vt92 | [1,…,92] | Yes | Yes, with height 6 |
| io2 | [1,2] | No | Yes, with height 1 |
| io7 | [1,…,7] | No | Yes, with height 2 |
| io17 | [1,…,17] | No | Yes, with height 3 |
| io20 | [1,…,20] | No | Yes, with height 4 |
| io44 | [1,…,44] | No | Yes, with height 5 |
| io92 | [1,…,92] | No | Yes, with height 6 |
| ih2 | [1,2] | Yes | No |
| ih7 | [1,…,7] | Yes | No |
| ih17 | [1,…,17] | Yes | No |
| ih20 | [1,…,20] | Yes | No |
| ih44 | [1,…,44] | Yes | No |
| ih92 | [1,…,92] | Yes | No |
These trees are used to define two lists:
val validTrees = [vt0, vt2, t2, t3, t4, t1, vt17, vt20, vt44, vt92]
val invalidTrees = [io2, io7, io17, io20, io44, io92,
ih2, ih9, ih17, ih20, ih44, ih92]In this problem you will (1) implement a validity test for 2-3 trees and (2) implement the effcient 2-3 insertion algorithm from the handout on 2-3 trees.
Your ~wx/cs251/sml/ps7 folder also includes the starter file TTTreeFuns.sml. In this file, flesh out the missing definitions as specified below. When you finish this problem, rename the file to yourAccountName-TTTreeFuns.sml before you submit it.
Be sure to perform execute the following in a shell in your wx appliance to get the ~wx/cs251/sml/ps7 folder:
cd ~/cs251/sml
git pull origin master-
satisfiesOrderingProperty(7 points)In this part, you will implement a function
satisfiesOrderingProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree ordering property andfalseif it does not. An easy way to do this is to define two helper functions:elts: TTTree -> int listreturns a list of all the elements of the tree in in-order — i.e.,- In a 2-node with left subtree l, value X, and right subtree r, all values in l are listed before X, which is listed before all elements in r.
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, all values in l are listed before X, which is listed before all values in m, which are listed before Y , which is listed before all values in r.
isSorted: int list -> boolreturnstrueif the list of integers is in sorted order andfalseotherwise.
For example:
- elts vt17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] : int list - elts io17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,17,16] : int list - isSorted(elts vt17); val it = true : bool - isSorted(elts io17); val it = false : boolUsing these two helper functions,
satisfiesOrderingPropertycan be implemented as:fun satisfiesOrderingProperty t = isSorted(elts t)For example:
- map satisfiesOrderingProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesOrderingProperty invalidTrees; val it = [false,false,false,false,false,false,true,true,true,true,true,true] : bool listNotes:
-
It is assumed that you are already familiar with running SML in Emacs from Problem 2.
-
Your workflow on this problem should be as follows:
-
Once (and only once), load the
TTTree.smlfile into an SML interpreter to load theTTTreedatatype and example trees.-
If you’re running SML in Emacs in wx (recommended), you can load
TTTree.smlvia these steps:-
Open
~wx/cs251/sml/ps7/TTTree.smlin Emacs: use theC-x C-fkeyboard shortcut or the menu itemFile>Open File) -
Load
TTTree.smlfile into a*sml*interpreter buffer: use theC-c C-bkeyboard shortcut (followed by areturnif prompted in the mini-buffer at the bottom of the screen) or the menu itemSML>Process>Send Buffer. You may need to scroll down in the*sml*buffer to see what has been loaded.
-
-
Otherwise, in an SML interpreter, do the following:
- Posix.FileSys.chdir "/home/wx/cs251/sml/ps7"; val it = () : unit - use "TTTree.sml"; ... lots of printout omitted ...Note that
Posix.FileSys.chdirneeds to be called only once for an interactive session.
-
-
Now open the file
TTTreeFuns.smland edit some definitions -
Every time you change the file
TTTreeFuns.smland want to test your changes in the SML interpreter, load this file into the interpreter using one of the two approaches described in Step 1.
-
-
You may need to execute
Control.Print.printLength := 100;in order to see all the list elements. -
Implement
isSortedusing the same zipping approach you used in PS4. As seen in Problem 2b, you do zipping in SML viaListPair.zipfrom the ListPair module.List.allfrom the List module is also helpful.
-
satisfiesHeightProperty(9 points)In this part, you will implement a function
satisfiesHeightProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree height property andfalseif it does not. An easy way to do this is to definesatisfiesHeightPropertyasfun satisfiesHeightProperty t = Option.isSome (height t)where
Option.isSomeis a function from the Option module that determines if anoptionvalue is aSOME(vs. aNONE) andheightis a function with typeTTTree -> option intsuch thatheight treturnsSOME hiftsatisfies the height property with heighthand otherwise returnsNONE.Implement the
heightfunction by fleshing out this skeleton:(* height: TTTree -> int option *) fun height L = (* return an appropriate option value here *) | height (W(l, _, r)) = (case (height(l), height(r)) of (* put appropriate pattern clauses here *)) | (* handle the H case here, similarly to the W case *)For example:
- map height validTrees; val it = [SOME 0,SOME 1,SOME 2,SOME 2,SOME 2,SOME 3,SOME 3,SOME 4,SOME 5,SOME 6] : int option list - map height invalidTrees; val it = [SOME 1,SOME 2,SOME 3,SOME 4,SOME 5,SOME 6,NONE,NONE,NONE,NONE,NONE,NONE] : int option listNotes:
-
It’s important to enclose the
caseexpressions withinheightin parens to distinguish the pattern clauses of thecaseexpression from those of theheightfunction definition. -
You should not exhaustively match patterns for four combinations of
SOME/NONEfor a two-node and nine combinations for a three-node. Instead use the underscore pattern_to match “everything else”. With the underscore, only two patterns are necessary for handling two-nodes and two patterns are necessary for handling three-nodes. -
Once
heightis defined,satisfiesHeightPropertyis defined:- map satisfiesHeightProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesHeightProperty invalidTrees; val it = [true,true,true,true,true,true, false,false,false,false,false,false] : bool list -
Once both
satisfiesOrderingPropertyandsatisfiesHeightPropertyare defined, it is trivial to define a functionisValid: TTTree -> boolthat returnstrueif a given 2-3 tree is valid andfalseotherwise.fun isValid t = satisfiesOrderingProperty t andalso satisfiesHeightProperty t - map isValid validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map isValid invalidTrees; val it = [false,false,false,false,false,false, false,false,false,false,false,false] : bool list
-
-
insert(14 points) In this part, you will implement the insertion algorithm for 2-3 trees as described on pages 3 to 5 of the handout on 2-3 trees. You will not implement the special cases described on page 6 .The insertion algorithm is a recursive algorithm that uses the notion of a pseudo 2-node that is “kicked up” in certain cases and handled specially in the upward phase of the recursion. To distinguish an insertion result that is a regular 2-3 tree from a pseudo 2-node that is “kicked up”, we use the following datatype:
datatype InsResult = Tree of TTTree | KickedUp of TTTree * int * TTTree (* pseudo 2-node "kicked up" from below *)You will implement 2-3 tree insertion via a pair of functions:
-
(insert v t)returns the newTTTreethat results from inserting a given intvinto a given treet.inserthas typeint -> TTTree -> TTTree. -
(ins v t)is a helper function that returns the instance ofInsResultthat results from inserting a given intvinto a given treet.inshas typeint -> TTTree -> InsResult.
Your implementation should flesh out the following code skeleton by turning the pictures on pages 3 to 5 from the handout on 2-3 trees into SML code.
(* insert: int -> TTTree -> TTTree *) fun insert v t = case ins v t of Tree t => t | KickedUp(l, w, r) => W(l, w, r) and (* "and" glues together mutually recursive functions *) (* ins: int -> TTTree -> InsResult *) ins v L = KickedUp (L, v, L) | ins v (W(l, X, r)) = if v <= X then (case ins v l of Tree l' => Tree(W(l', X, r)) | KickedUp (l', w, m) => Tree(H(l', w, m, X, r))) else (* flesh this out *) | (* handle an H node similarly to the W node based on rules from the handout *)Notes:
-
The
insfunction should only callinsrecursively and should not callinsert. -
An easy way to test
insertis to call the followinglistToTTTreefunction on a list of numbers generated byrange. (These are already defined in your starter file.) Note that you may need to increase the print depth (viaControl.Print.printDepth := 100) in order to see all the details of the printed trees:fun listToTTTree xs = foldl (fn (x,t) => insert x t) L xs fun range lo hi = if lo >= hi then [] else lo :: (range (lo + 1) hi) - listToTTTree (range 1 8); val it = W (W (W #,2,W #),4,W (W #,6,W #)) : TTTree - listToTTTree (range 1 17); val it = W (W (W #,4,W #),8,W (W #,12,W #)) : TTTree - Control.Print.printDepth := 100; val it = () : unit - listToTTTree (range 1 7); val it = H (W (L,1,L),2,W (L,3,L),4,H (L,5,L,6,L)) : TTTree - listToTTTree (range 1 18); val it = W (W (W (W (L,1,L),2,W (L,3,L)),4,W (W (L,5,L),6,W (L,7,L))),8, W (W (W (L,9,L),10,W (L,11,L)),12, H (W (L,13,L),14,W (L,15,L),16,W (L,17,L)))) : TTTree - listToTTTree (range 1 45); val it = W (W (W (W (W (L,1,L),2,W (L,3,L)),4,W (W (L,5,L),6,W (L,7,L))),8, W (W (W (L,9,L),10,W (L,11,L)),12,W (W (L,13,L),14,W (L,15,L)))),16, H (W (W (W (L,17,L),18,W (L,19,L)),20,W (W (L,21,L),22,W (L,23,L))),24, W (W (W (L,25,L),26,W (L,27,L)),28,W (W (L,29,L),30,W (L,31,L))),32, H (W (W (L,33,L),34,W (L,35,L)),36,W (W (L,37,L),38,W (L,39,L)),40, W (W (L,41,L),42,H (L,43,L,44,L))))) : TTTree -
Unfortunately, inserting elements in sequential order as above tends to create 2-3 trees with almost all 2-nodes and very few 3-nodes. It turns out a better way is to mix up the order of insertion as is done in the following code for
makeTTTree. This results in trees that have a good mix of 2-nodes and 3-nodes:(* Return list that has all ints in nums, but those not divisible by 3 come before those divisible by three *) fun arrangeMod3 nums = let val (zeroMod3, notZeroMod3) = List.partition (fn n => (n mod 3) = 0) nums in notZeroMod3 @ zeroMod3 end (* Make a 2-3 tree with elements from 1 up to and including size. Use arrangeMod3 to mix up numbers and lead to more 3-nodes than we'd get with sorted integers lists *) fun makeTTTree size = listToTTTree (arrangeMod3 (range 1 (size + 1))) - makeTTTree 17; val it = H (W (W (L,1,L),2,H (L,3,L,4,L)),5,W (H (L,6,L,7,L),8,H (L,9,L,10,L)),11, H (H (L,12,L,13,L),14,W (L,15,L),16,W (L,17,L))) : TTTree - makeTTTree 44; val it = W (W (W (W (W (L,1,L),2,H (L,3,L,4,L)),5,W (H (L,6,L,7,L),8,H (L,9,L,10,L))), 11, W (W (H (L,12,L,13,L),14,H (L,15,L,16,L)),17, W (H (L,18,L,19,L),20,H (L,21,L,22,L)))),23, W (W (W (H (L,24,L,25,L),26,H (L,27,L,28,L)),29, W (H (L,30,L,31,L),32,H (L,33,L,34,L))),35, W (W (H (L,36,L,37,L),38,H (L,39,L,40,L)),41, W (W (L,42,L),43,W (L,44,L))))) : TTTree -
Finally, to test your insertion implementation more extensively, try
(testInsert 1000)with the following function, which will usemakeTTTreeto create 2-3 trees containing 0 elements to 1000 elements and warn you of any invalid trees.fun testInsert upToSize = let val pairs = map (fn n => (n, makeTTTree n)) (range 0 (upToSize + 1)) val (validPairs, invalidPairs) = List.partition (fn (_,t) => isValid t) pairs val wrongElts = List.filter (fn (n,t) => (elts t) <> (range 1 (n + 1))) validPairs in if (null invalidPairs) andalso (null wrongElts) then (print "Passed all test cases\n"; []) else if (not (null invalidPairs)) then (print "There are invalid trees in the following cases\n"; invalidPairs) else (print "The elements or element order is wrong in the following cases\n"; wrongElts) end - testInsert 1000; Passed all test cases val it = [] : (int * TTTree) list
-
Extra Credit 1: Implementing PostLoop for in the All-commands-as-stack-transformers Interpreter (10 points)
It is possible to implement the PostLoop for loop from Problem 2 in a version of the interpreter based on the all-commands-as-stack-transformers PostFix interpreter presented in slides 22–23 of the PostFix slides. This means that the for command must be implemented as a stack transformer as well.
Begin this problem by downloading ps7-postloop-tranform-fancy-starter.rkt, which you should rename to yourAccountName-ps7-postloop-transform-fancy.rkt.
In this file, you should flesh out the implementation of the for command in the function postloop-exec-command. Your for clause should use the helper function postloop-loop-commands, whose provided stub definition you also need to replace:
(define (postloop-loop-commands num seq stk)
;; Assume num is the nonnegative integer argument of a for loop
;; and seq is the command sequence argument of a for loop.
;; Returns the final stack that results from running the for loop
;; with these arguments starting with the initial stack stk
;; of values that *follow* these two arguments.
stk ; Replace this stub!
)The testing notes from Problem 1d also apply here. In particular, you should copy your definitions of postloop-fact, postloop-expt, postloop-pairs-up, and postloop-fib from Problem 1d into yourAccountName-ps7-postloop-transform-fancy.rkt, and uncomment and run (test-loops loop-tests) at the end of the file. Your implementation should handle error cases as specified in Problem 1d.
Extra Credit 2: Implementing sum-between in PostLoop (10 points)
Implement and test a PostLoop program postloop-sum-between that takes two integer arguments we’ll call lo and hi. Either argument can be any integer (positive, zero, negative). You can assume both arguments are integers (no error checking necessary).
-
If
hi>=lo, then the program should return the sum of the integers betweenloandhi, inclusive. -
If
hi<lo, then the program should return 0.
Below are examples of the input/output behavior of this program
| Args | Result |
|---|---|
| (0 5) | 15 |
| (0 100) | 5050 |
| (17 17) | 17 |
| (3 7) | 25 |
| (-7 -3) | -25 |
| (-3 4) | 4 |
| (-4 3) | -4 |
| (-3 3) | 0 |
| (7 3) | 0 |
| (-3 -7) | 0 |
Notes:
-
There is a closed-form formula for calculating the result without a loop, but your program is not allowed to use this formula. Instead, your program must use a
forloop that adds together each of the integers in the rangelotohi(inclusive), starting with zero. -
Depending on your approach, you may find it helpful to add the numbers from
hidown tolorather than fromloup tohi. -
It may be helpful to store what are effectively ``local variables’’ on the stack that you calculate once before the loop but reference on each iteration of the loop.
-
You should test your program on the examples shown above. One way to do this is to extend the
loop-teststest cases from the interpreter in Problem 2 or Extra Credit Problem 1 so that thetest-loopsfunction will test it.
Extra Credit 3: 2-3 Tree Deletion (20 points)
In SML, implement and test the 2-3 tree deletion algorithm presented in pages 8 through 11 of the handout on 2-3 trees.
Extra Credit 4: 2-3 Trees in Java (35 points)
Implement and test 2-3 tree insertion and deletion in Java. Compare the SML and Java implementations. Which features of which languages make the implementation easier and why?