CS 251: PS9: I Never Metalanguage I Didn't Like

Dueish: Thu May 02, 2019
Notes:
- This pset has 105 total points.
- This pset contains two solo problems worth 40 points total
- The problems needn’t be done in order. Feel free to jump around.

Times from Spring ‘18 (in hours, n=22)

Times	Problem 1	Problem 2	Problem 3	Problem 4	Problem 5	Total
average time (hours)	3.0	3.8	2.3	1.2	1.9	11.3
median time (hours)	2.5	3.0	2.0	1.0	1.8	9.9
25% took more than	3.9	4.3	2.75	1.3	2.0	13.4
10% took more than	4.9	6.0	3.5	2.0	3.0	18.75

Submission:
- In your yourFullName CS251 Spring 2019 Folder, create a Google Doc named yourFullName CS251 PS9.
- At the top of your yourFullName CS251 PS9 doc, include your name, problem set number, date of submission, and an approximation of how long each problem part took.
- For all parts of all problems, include all answers (including SML code) in your PS9 google doc. Format code using a fixed-width font, like Consolas or Courier New. You can use a small font size if that helps.
- For Problem 3, include your interpretation/compilation derivations. It is easiest to write these top-down via nested bullets, as shown in both the pset description and the lecture notes.
- For Problem 5:
  - For parts a, b, and d, include a single AST for P_Intex (from part a) that is annotated with depth information (from part b) and stack information (from part d).
  - For part c, include the commented PostFix program P_PostFix that is the result of translating P_Intex to PostFix.
- In Problems 1, 2, and 4, you will create the following code files from starter files populating your ~/cs251/sml/ps9 directory on your csenv/wx Virtual Machine:
  - Problem 1: yourAccountName-marbles.sml
  - Problem 2: yourAccountName-LazySequence.sml
  - Problem 4: yourAccountName-IntexArgChecker.sml
  For these problems:
  - include all functions from the four files named yourAccountName... in your Google Doc (so that I can comment on them).
  - Drop a copy of your ~/cs251/sml/ps9 folder in your ~/cs251/drop/ps09 drop folder on cs.wellesley.edu by executing the following (replacing both occurrences of gdome by your cs server username):
```
scp -r ~/cs251/sml/ps9 gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps09
```

Starting this Problem Set

Problems 1, 2, and 4 involve starter files in the ~/cs251/sml/ps9 directory in your csenv/wx Virtual Machine.

To create this directory, follow the git instructions in this doc If you encounter any problems with this step, please contact Lyn.

REMINDER: ALWAYS MAKE A BACKUP OF YOUR .sml FILES AT THE END OF EACH DAY TO AVOID POTENTIAL LOSS OF WORK.

1. Solo Problem: Losing Your Marbles (15 points)

This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.

Begin this problem by renaming the starter file marbles.sml in ~/cs251/sml/ps9 to yourAccountName-marbles.sml. Put all your definitions for this problem in the renamed starter file.

In this problem, you will define an SML function satisfying the following specification:

val marbles: int -> int -> int list list

Assume that m is a non-negative integer and that c is a positive integer. Given m marbles and a row of c cups, marbles m c returns a sorted list of all configurations whereby all m marbles are distributed among the c cups. Each configuration should be a list of length c whose elements are integers between 0 and m and the sum of whose elements is m. The returned list should be ordered lexicographically (i.e., in dictionary order).

At the end of this problem description are numerous sample invocations of the marbles function.

Your task is to define the marbles function in SML so that it satisfies the above specification and has the same behavior as the sample invocations below.

  (* Execute the following to display elements beyond the default cutoff length for lists *)
  - Control.Print.printLength := 100; 
  val it = () : unit

  - marbles 0 1;
  val it = [[0]] : int list list

  - marbles 0 2;
  val it = [[0,0]] : int list list

  - marbles 0 3;
  val it = [[0,0,0]] : int list list

  - marbles 0 4;
  val it = [[0,0,0,0]] : int list list

  - marbles 1 1;
  val it = [[1]] : int list list

  - marbles 1 2;
  val it = [[0,1],[1,0]] : int list list

  - marbles 1 3;
  val it = [[0,0,1],[0,1,0],[1,0,0]] : int list list

  - marbles 1 4;
  val it = [[0,0,0,1],[0,0,1,0],[0,1,0,0],[1,0,0,0]] : int list list

  - marbles 2 1;
  val it = [[2]] : int list list

  - marbles 2 2;
  val it = [[0,2],[1,1],[2,0]] : int list list

  - marbles 2 3;
  val it = [[0,0,2],[0,1,1],[0,2,0],[1,0,1],[1,1,0],[2,0,0]] : int list list

  - marbles 2 4;
  val it =
    [[0,0,0,2],[0,0,1,1],[0,0,2,0],[0,1,0,1],[0,1,1,0],[0,2,0,0],[1,0,0,1],
     [1,0,1,0],[1,1,0,0],[2,0,0,0]] : int list list

  - marbles 3 1;
  val it = [[3]] : int list list

  - marbles 3 2;
  val it = [[0,3],[1,2],[2,1],[3,0]] : int list list

  - marbles 3 3;
  val it =
    [[0,0,3],[0,1,2],[0,2,1],[0,3,0],[1,0,2],[1,1,1],[1,2,0],[2,0,1],[2,1,0],
     [3,0,0]] : int list list

  - marbles 3 4;
  val it =
    [[0,0,0,3],[0,0,1,2],[0,0,2,1],[0,0,3,0],[0,1,0,2],[0,1,1,1],[0,1,2,0],
     [0,2,0,1],[0,2,1,0],[0,3,0,0],[1,0,0,2],[1,0,1,1],[1,0,2,0],[1,1,0,1],
     [1,1,1,0],[1,2,0,0],[2,0,0,1],[2,0,1,0],[2,1,0,0],[3,0,0,0]]
    : int list list

  - marbles 4 1;
  val it = [[4]] : int list list

  - marbles 4 2;
  val it = [[0,4],[1,3],[2,2],[3,1],[4,0]] : int list list

  - marbles 4 3;
  val it =
    [[0,0,4],[0,1,3],[0,2,2],[0,3,1],[0,4,0],[1,0,3],[1,1,2],[1,2,1],[1,3,0],
     [2,0,2],[2,1,1],[2,2,0],[3,0,1],[3,1,0],[4,0,0]] : int list list

  - marbles 4 4;
  val it =
    [[0,0,0,4],[0,0,1,3],[0,0,2,2],[0,0,3,1],[0,0,4,0],[0,1,0,3],[0,1,1,2],
     [0,1,2,1],[0,1,3,0],[0,2,0,2],[0,2,1,1],[0,2,2,0],[0,3,0,1],[0,3,1,0],
     [0,4,0,0],[1,0,0,3],[1,0,1,2],[1,0,2,1],[1,0,3,0],[1,1,0,2],[1,1,1,1],
     [1,1,2,0],[1,2,0,1],[1,2,1,0],[1,3,0,0],[2,0,0,2],[2,0,1,1],[2,0,2,0],
     [2,1,0,1],[2,1,1,0],[2,2,0,0],[3,0,0,1],[3,0,1,0],[3,1,0,0],[4,0,0,0]]
    : int list list

  - marbles 5 1;
  val it = [[5]] : int list list

  - marbles 5 2;
  val it = [[0,5],[1,4],[2,3],[3,2],[4,1],[5,0]] : int list list

  - marbles 5 3;
  val it =
    [[0,0,5],[0,1,4],[0,2,3],[0,3,2],[0,4,1],[0,5,0],[1,0,4],[1,1,3],[1,2,2],
     [1,3,1],[1,4,0],[2,0,3],[2,1,2],[2,2,1],[2,3,0],[3,0,2],[3,1,1],[3,2,0],
     [4,0,1],[4,1,0],[5,0,0]] : int list list

  - marbles 5 4;
  val it =
    [[0,0,0,5],[0,0,1,4],[0,0,2,3],[0,0,3,2],[0,0,4,1],[0,0,5,0],[0,1,0,4],
     [0,1,1,3],[0,1,2,2],[0,1,3,1],[0,1,4,0],[0,2,0,3],[0,2,1,2],[0,2,2,1],
     [0,2,3,0],[0,3,0,2],[0,3,1,1],[0,3,2,0],[0,4,0,1],[0,4,1,0],[0,5,0,0],
     [1,0,0,4],[1,0,1,3],[1,0,2,2],[1,0,3,1],[1,0,4,0],[1,1,0,3],[1,1,1,2],
     [1,1,2,1],[1,1,3,0],[1,2,0,2],[1,2,1,1],[1,2,2,0],[1,3,0,1],[1,3,1,0],
     [1,4,0,0],[2,0,0,3],[2,0,1,2],[2,0,2,1],[2,0,3,0],[2,1,0,2],[2,1,1,1],
     [2,1,2,0],[2,2,0,1],[2,2,1,0],[2,3,0,0],[3,0,0,2],[3,0,1,1],[3,0,2,0],
     [3,1,0,1],[3,1,1,0],[3,2,0,0],[4,0,0,1],[4,0,1,0],[4,1,0,0],[5,0,0,0]]
    : int list list

Notes:

As usual, you should use divide/conquer/glue as your problem-solving strategy. Don’t attempt to write any code until you understand your strategy.
Don’t forget the very powerful notion of “wishful” thinking, in which you apply a recursive function to smaller versions of the same problem and combine their results. Study the examples carefully to see how the result of a call to marbles is stitched together from the results of calls to “smaller” versions of marbles.
Strive to make your solution as simple as possible. For example, do not use more base cases than are strictly necessary.
You are expected to use higher-order list functions where they can simplify your definition.
Here are things you should not do in your marbles definition:
- you should not generate duplicate lists that you later filter out
- you should not check for duplicates before adding an element to the result list.
- you should not reverse any lists
- you should not sort any lists
- you should not use an iterative strategy; use a recursive strategy instead!

The starter file begins with the following helper functions, which you might find useful:

fun cons x ys = x :: ys (* curried list consing operator *)
                      
fun range lo hi = (* list all ints from lo up to (but not including) hi *)
  List.tabulate(hi - lo, fn i => i + lo)

Reminder: these and other helper functions must be defined above your definition of marbles, because definition order matters in SML.

Feel free to define any additional auxiliary functions you find helpful.
To test your marbles.sml program, use the MarblesTest.sml file. In this file, change the line
```
use "marbles.sml";
```
to
```
use "yourAccountName-marbles.sml";
```
After you make this change, run MarblesTest.sml to test your marbles function on 30 test cases. Any test cases that fail will show the expected and actual results.
If you have previously used LazySequenceTest to test Solo Problem 2 in the same *sml* buffer, you will need to kill the *sml* buffer first before you load MarblesTest.sml. Why? Because the LazySequence problem redefines the map function that you might use in your marbles function.

2. Solo Problem: Lazy Sequences (25 points)

Background

This is a module/ADT problem that shares aspects of the FunSet and OperationTreeSet problems from PS8. It involves a data structure implementation involving multiple tree nodes, where some of the tree nodes have functional components.

The problem involves a list-like data structure called a sequence that has the following signature:

signature SEQUENCE = sig
    (* The type of a sequence *)
    type ''a t 

    (* An empty sequence *)
    val empty : ''a t

    (* Create a sequence of (hi - lo) values fcn(lo), fcn(lo+1), ..., fcn(hi-1) *)
    val segment: int -> int -> (int -> ''a) -> ''a t

    (* Convert a length-n list into a sequence of n values *)                          
    val fromList: ''a list -> ''a t

    (* Concatenate two sequences: given a length-m sequence s and length-n sequence t, 
       returns a single length-m+n sequence that has all values of s followed by all 
       values of t *)
    val concat : ''a t -> ''a t -> ''a t

    (* Return the length of a sequence = number of values in it *)                              
    val length : ''a t -> int

    (* Return the nth value of a sequence (0-indexed). 
       Raise an IndexOutOfBounds exception for an out-of-bounds index. *)                                
    val get : int -> ''a t -> ''a

    (* Return a sequence that results from applying f to each elt *)
    val map : (''a -> ''b) -> ''a t -> ''b t

    (* Return a list with all elements in the sequence. The ith element of the resulting
       list should be the ith element of the given sequence. *)
    val toList : ''a t -> ''a list

end

It would be straightforward to implement a sequence as a list. But this implementation can have issues.

As a concrete example, consider the following inefficient ways to increment and double a number:

(* A slow incrementing function *)
fun linearIncrement n =
  let fun loop num ans =
  if num = 0 then ans else loop (num-1) (ans+1)
  in loop n 1
 end

(* A very slow doubling function *)
fun quadraticDouble n =
  let fun loop num ans =
  if num = 0 then ans else loop (num-1) (linearIncrement ans)
  in loop n n
 end

For example, quadraticDouble 10000 returns fairly quickly, but quadraticDouble 100000 takes many seconds.

Now suppose we want to create the sequence

val reallyBigSeq = segment ~200000000 200000000 quadraticDouble

There are two big problems if we try to represent this as a list. First, the list would need to contain 400 million elements. Second, calculating each entry in the list (especially for large inputs) would take a very long time. So the list implementation is bad in terms of both space and time.

An alternative implementation is not to calculate and store each element when the sequence is created, but to calculate each element on the fly only when the get operation is called to return it. This is the basis of the LazySequence structure that you will implement in this problem. It is based on the following datatype:

datatype ''a t = Segment of int * int * (int -> ''a) (* lo, hi, fcn *)
       | ThunkList of (unit -> ''a) list
       | Concat of ''a t * ''a t

In programming languages, the term “lazy” means “not computed until necessary”. In this context, an element of a sequence will not be calculated until it needs to be known.

The `Segment` constructor

In the case of reallyBigSeq, the sequence can be represented via the sum-of-product value

Segment(~200000000,200000000,quadraticDouble)

This simply keeps track of the information for constructing the sequence. Now if we wish to get the value of this sequence at index 20000017, we can apply quadraticDouble to (200000017 + ~200000000) = 17 and return the value quadraticDouble(17). This way, we only “pay” for calculations done at the indices on which we actually perform get. This leads to the following implementation of the segment function:

fun segment lo hi fcn = Segment(lo,hi,fcn)

Thunks

Lazy data structures often employ something called a thunk, which is simply a function of zero arguments. Wrapping a calculation in a function of zero arguments is a way to delay it until later ratger than performing it now. For example, consider testThunk:

val testThunk = fn () => quadraticDouble 100000

Even though calculating quadraticDouble 100000 takes many seconds, defining testThunk is immediate, because no calculation is performed until testThunk is called, as in testThunk(). This is called “dethunking”, which can be defined as follows:

fun dethunk thunk = thunk()

So testThunk() can equivalently be written dethunk(testThunk)

Note that every SML function necessarily takes exactly one argument, so the notion that thunks take “zero” arguments is loose terminology. In fact a thunk takes the “unit value”, written (), which is the only value of type unit and can be viewed as a tuple with zero components.

The upside of a thunk is that the delayed computation is never performed if the thunk is never dethunked. The downside is that the calculation is performed every time the thunk is dethunked, so computations can be repeated unnecessarily.

Note that the type of testThunk is unit -> int, where unit specifies that the () value must be supplied to the thunk in order to extract its value. In general, the type of a thunk for a value of type ''a is unit -> ''a, so we use this as the definition of a type abbreviation named thunkTy:

type ''a thunkTy = unit -> ''a

The `ThunkList` constructor

Whereas the Segment constructor supports “regular” lazy sequences whose values are determined by some function over a range of integers, the ThunkList constructor is intended to support more “irregular” sequences in which there is not a simple correspondence between sequence values and a range of integers. For example, consider these sequences:

val numSeq = fromList [300005, 20074, 4000017, 1002]
val quadSeq = map quadraticDouble numSeq

Suppose we want all the applications of quadraticDouble to be delayed until the sequence elements are extracted. E.g., get 1 quadSeq should calculate quadraticDouble 20074 when the get is performed, but not before that. If the elements at indices 0 and 2 are never accessed via get, then the time-intensive calculations quadraticDouble 300005 and quadraticDouble 4000017 are never performed.

The ThunkList constructor takes a list of thunks:

ThunkList of ''a thunkTy list

Using ThunkList, the quadSeq sequence can be represented as something like:

ThunkList[ fn () => quadraticDouble 300005,      
           fn () => quadraticDouble 20074,      
           fn () => quadraticDouble 4000017, 
           fn () => quadraticDouble 1002 ]

Based on this idea, we can use ThunkList to represent all “irregular” sequences constructed from lists via fromList:

fun fromList xs = ThunkList (List.map (fn x => (fn () => x)) xs)

This means that in numSeq, all the numbers will be thunked, and so will be equivalent to:

ThunkList[ fn () => 300005,      
           fn () => 20074,      
           fn () => 4000017, 
           fn () => 1002 ]]

The `Concat` constructor

The final constructor in the ''a t sum-of-product sequence datatype is the Concat constructor:

Concat of ''a t * ''a t

This is simply used to glue together two sequences:

fun concat seq1 seq2 = Concat(seq1,seq2)

Summary

In the end, any instance of the ''a t sum-of-product sequence datatype is a binary tree of Concat nodes whose leaves are either Segment nodes or ThunkList nodes.

In this way, an instance of the sequence datatype is a tree in the same way that instances of OperationTreeSet were trees in PS8 Problem 4.

Because both the Segment and ThunkList constructors involve functions that delay computation until a result is needed, they are similar to the FunSet implementation of sets in PS8 Problem 3.

Your task

The starter file for this problem is LazySequence.sml in the ~/cs251/sml/ps9 directory in your csenv/wx Virtual Machine.

Begin this problem by renaming the starter file LazySequence.sml in ~/cs251/sml/ps9 to yourAccountName-LazySequence.sml. Put all your definitions for this problem in the renamed starter file.

LazySequence.sml contains the SEQUENCE signature from above and the following partial implementation of the LazySequence structure:

  structure LazySequence :> SEQUENCE = struct

     type ''a thunkTy = unit -> ''a

     datatype ''a t = Segment of int * int * (int -> ''a) (* lo, hi, fcn *)
                 | ThunkList of ''a thunkTy list
                      | Concat of ''a t * ''a t

     fun segment lo hi fcn = Segment(lo,hi,fcn)
     fun fromList xs = ThunkList (List.map (fn x => (fn () => x)) xs)
     fun concat seq1 seq2 = Concat(seq1,seq2)
     fun dethunk thunk = thunk()                            

     val empty = ThunkList []

     fun length seq = 0 (* replace this stub *)

     fun get n seq = raise Unimplemented (* replace this stub *)

     fun map f seq = empty (* replace this stub *)

     fun toList seq = [] (* replace this stub *)

  end

The segment, fromList, concat functions and empty value have already been defined for you. Your task is to implement the remaining four functions: length, get, map, and toList. Pay attention to the following notes in your implementation.

Notes:

Be careful to use the explicitly qualified List.map and List.length functions when operating on a list, but unqualified map and length operators when operating on a sequence. Any attempt to use the unqualified map and length on a list will result in a type error (because SML will assume they are the sequence operators and not the list operators).
Do not use the toList function in the implementations of length, get, and map. Similarly, the get function should not be used in the implementation of toList. However, you may use the length function in the implementation of get.
The length function should always return an integer and should never raise an exception.
The get function should raise an IndexOutOfBounds exception for a sequence s when called on a index outside the range 0 and length(s) - 1. To raise this exception for an out-of-bounds index n, use raise (IndexOutOfBounds n). In the implementation of the get function, full credit will be awarded only if the out-of-bounds length check is performed only one (not separately for each of the three constructors). You may use the length function in the implementation of get.
The map function should always return a sequence and should never raise an exception, even if the mapped function might raise an error on one of the values. For example, in
```
val mapSeq2 = map (fn n => 20 div n) (fromList [3, 0, 5, 2, 4])
```
no exception should be raised when defining mapSeq2 or evaluating get 0 mapSeq2, get 2 mapSeq2, get 3 mapSeq2, or get 4 mapSeq2. But get 1 mapSeq2 should raise a divide-by-zero exception.
The map function should preserve the “shape” of its input sum-of-product constructor tree. So it should return a Concat output for a Concat input, a Segment output for a Segment input, and a ThunkList output for a ThunkList input.
In the implementation of the map function, it will be necessary to combine two function values into one. What is the most natural way to do this? (Hint: it’s something we’ve studied before!)
If calculating one or more values of a sequence s raises an exception, toList s should raise the exception associated with the value having the lowest index.
To test your sequence implementation in yourAccountName-LazySequence.sml, follow these steps:
- In the file LazySequenceTest.sml, change the line use "LazySequence.sml"; to use "yourAccountName-LazySequence.sml";
- Run the file LazySequenceTest.sml.
  - If running LazySequenceTest.sml reports a syntax or type error, there are syntax or type errors in your LazySequence.sml program that need to be fixed before you can test it.
  - Running LazySequenceTest.sml should print the results of running 153 test cases. If some of the test cases don’t pass, scan back for the string FAIL to see expected and actual results for the test cases that failed.
  - If the printing of test cases hangs for a long time without completing, it means that you are not being lazy enough in your implementation, and the test case on which it hangs is taking much longer than it should.
Here is a FAQ associated with this problem:

Q1: What is the structure of a lazy sequence?

A1: Just as an OperationTreeSet is a tree made out of six kinds of nodes, a LazySequence is a tree made out of the three kinds of nodes in this datatype:
```
datatype ''a t = Segment of int * int * (int -> ''a) (* lo, hi, fcn *)
               | ThunkList of (unit -> ''a) list
               | Concat of ''a t * ''a t
```
The Segment, ThunkList, and Concat constructors represent three completely different ways to represent a lazy sequence.
- A Segment represents a length-n lazy sequence as a single unary (single-argument) function that is applied to every index in a range with n indices.
- A ThunkList represents a length-n lazy sequence as a list of n nullary (zero-argument) functions (known as thunks).
- A Concat represents a length-(m+n) lazy sequence as the combination of a length-m lazy sequence and a length-n lazy sequence.
Q2: Can lazy sequences have infinite length?

A2: No. Based on the answer to Q1, all lazy sequences have a finite number of elements.

Q3: Why do I get the error data constructor Segment used without argument in pattern?

A3: Be sure to wrap pattens in parens. E.g., write (Segment(lo,hi,func)), not Segment(lo,hi,func)

Q4: When I send LazySequence.sml to the *sml* buffer, I don’t get an interpreter prompt in the *sml* buffer. Why?

A4: Look for an infinite loop in your code that is causing it to hang.

Q5: When I run LazySequenceTest.sml, it gets stuck and doesn’t print out a summary of how many test cases have passed/failed. Why?

A5: This likely means that your implementation is not being sufficiently lazy, and that the tester is taking a long time to complete calculations it should not be computing.

3. Metaprogramming Derivations (32 points)

3a. Deriving Implementations (16 points)

As we discussed in the Metaprogramming lecture, there are two basic reasoning rules involving interpreters, translators (a.k.a. compilers), and program implementation:

The Interpreter Rule (I)

$\frac{P\text{-in-}L\text{ program} \qquad L\text{ interpreter machine}}{P\text{ machine}} (I)$

The Translator Rule (T)

$\frac{P\text{-in-}S\text{ program} \qquad S\text{-to-}T\text{ translator machine}}{P\text{-in-}T\text{ program}} (T)$

In practice, we often elide the word “machine” for interpreter machines and translator machines. For example, we will refer to an “L interpreter machine” as an “L interpreter”, and an “S-to-T translator machine” as an “S-to-T translator” or “S-to-T compiler”. We will also often elide the word “program”; e.g., we will refer to a “P-in-L program” as “P-in-L”. So an “L interpreter” means an “L interpreter machine” while a “S-in-L interpreter” means an “S-in-L interpreter program”. Similar remarks hold for translators (also called compilers): an “S-to-T translator” means an “S-to-T translator machine”, while a “S-to-T-in-L translator” means an “S-to-T-in-L translator program”.

Example

For example, we considered the following elements in class:

a 251-web-page-in-HTML program (i.e., a 251 web page written in HTML)
an HTML-interpreter-in-C program (i.e., a web browser written in C)
a C-to-x86-compiler-in-x86 program (i.e., a C-to-x86 compiler written in x86)
a x86 computer (i.e., an x86 interpreter machine)

They can be used to build a 251 web page display machine as follows:

$\cfrac{ \text{251-web-page-in-HTML program} \qquad \cfrac{ \cfrac{ \text{HTML-interpreter-in-C program} \qquad \cfrac{ \text{C-to-x86-compiler-in-x86 program} \qquad \text{x86 computer} }{ \text{C-to-x86 compiler machine} } (I) }{ \text{HTML-interpreter-in-x86 program} } (T) \qquad \text{x86 computer} }{ \text{HTML interpreter machine} } (I) }{ \text{251 web page machine} } (I)$

Feel free to abbreviate by dropping the words “program” and “machine”. “… in …” denotes a program, while “… compiler” and “… translator” denote translator machines and “… interpreter” and “… computer” denote interpreter machines.

$\cfrac{ \text{251 web page in HTML} \qquad \cfrac{ \cfrac{ \text{HTML interpreter in C} \qquad \cfrac{ \text{C-to-x86 compiler in x86} \qquad \text{x86 computer} }{ \text{C-to-x86 compiler} } (I) }{ \text{HTML interpreter in x86} } (T) \qquad \text{x86 computer} }{ \text{HTML interpreter} } (I) }{ \text{251 web page machine} } (I)$

Writing Derivations

Rather that displaying derivations using horizontal lines, it is recommended that you use nested bullets to indicate the same structure as the inference rules (though drawn “upside down”). For example, the derivation above could also be written:

251 web page machine (I)

251-web-page-in-HTML program
HTML interpreter machine (I)
- HTML-interpreter-in-x86 program (T)
  - HTML-interpreter-in-C program
  - C-to-x86 compiler machine (I)
    - C-to-x86-compiler-in-x86 program
    - x86 computer
- x86 computer

Questions

i. (8 points) Suppose you are given the following:

A P-in-Java program
a Java-to-C-compiler-in-Racket program (i.e., a Java-to-C compiler written in Racket);
a Racket-interpreter-in-x86 program (i.e., a Racket interpreter written in x86 machine code);
a C-to-x86-compiler-in-x86 program (i.e., a C-to-x86 compiler written in x86 code);
an x86 computer (i.e., an x86 interpreter machine).

Using the two reasoning rules above, construct a “proof” that demonstrates how to execute the P-in-Java program on the computer. That is, show how to construct a P machine.

ii. (8 points) Suppose you are given:

a GraphViz-in-C program
a C-to-LLVM-compiler-in-x86 program
an LLVM-to-JavaScript-compiler-in-x86 program
a JavaScript-interpreter-in-ARM program
an x86 computer (i.e., an x86 interpreter machine, such as your laptop)
an ARM computer (i.e., an ARM interpreter machine, such as a smartphone)

Show how to construct a GraphViz machine.

Notes:

In the above two parts, it is not possible to derive a “C interpreter”, a “Java interpreter”, or an “LLVM interpreter”, so if you need or use such a part in your derivation, you’ve done something wrong.
As shown in the above examples, you should use an (I) or (T) to indicate a conclusion that results from the Interpreter or Translator rule, respectively. Double check that the conclusion is actually justified by the rule from two nested bullets below the conclusion.

3b. Bootstrapping (16 points)

In his Turing Award lecture-turned-short-paper Reflections on Trusting Trust, Ken Thompson describes how a compiler can harbor a so-called “Trojan horse” that can make compiled programs insecure. Read this paper carefully and do the following tasks to demonstrate your understanding of the paper:

i. (6 points) Stage II of the paper describes how a C compiler can be “taught” to recognize '\v' as the vertical tab character. Using the same kinds of components and processes used in Problem 1, we can summarize the content of Stage II by carefully listing the components involved and describing (by constructing a proof) how a C compiler that “understands” the code in Figure 2.2 can be generated. (Note that the labels for Figures 2.1 and 2.2 are accidentally swapped in the paper.) In Stage II, two languages are considered:

the usual C programming language
C+\v = an extension to C in which '\v' is treated as the vertical tab character (which has ASCII value 11).

Suppose we are given the following:

a C-to-binary compiler machine (Here, “binary” is the machine code for some machine. This compiler is just a “black box”; we don’t care where it comes from);
a C+\v-to-binary-compiler-in-C program (Figure 2.3 in Thompson’s paper);
a C+\v-to-binary-compiler-in-C+\v program (what should be Figure 2.2 in Thompson’s paper);
a machine that executes the given type of binary code (i.e., a binary interpreter machine)

Construct a proof showing how to use the C+\v-to-binary-compiler-in-C+\v source code to create a C+\v-to-binary-compiler-in-binary program.

ii. (10 points) Stage III of the paper describes how to generate a compiler binary harboring a “Trojan horse”. Using the same kinds of components and processes used in Problem 1, we can summarize the content of Stage III by carefully listing the components involved and describing (by constructing a proof) how the Trojaned compiler can be generated. In particular, assume we have the parts for this stage:

a C-to-binary-compiler machine (again, just a “black box” we are given);
a C-to-binary-compiler-in-C program without Trojan Horses (Figure 3.1 in Thompson’s paper);
a C-to-binary-compiler_TH-in-C program with two Trojan Horses (Figure 3.3 in Thompson’s paper);
a login-in-C program with no Trojan Horse;
a binary-based computer (i.e., a binary interpreter machine)

The subscript _TH indicates that a program contains a Trojan Horse. A C-to-binary compiler_TH has the “feature” that it can insert Trojan Horses when compiling source code that is an untrojaned login program or an untrojaned compiler program. That is, if P is a login or compiler program, it is as if there is a new rule:

The Trojan Horse Rule (TH)

$\cfrac{ P\text{-in-C program} \qquad \text{C-to-binary-compiler}_{TH}\ \text{machine} }{ P_{TH}\text{-in-binary} } (TH)$

Using these parts along with the two usual rules (I) and (T) and the new rule (TH), show how to derive a Trojaned login program login_TH-in-binary that is the result of compiling the uninfected login-in-C program with a C compiler that is itself the result of compiling the uninfected C-to-binary-compiler-in-C program. The interesting thing about this derivation is that login_TH-in-binary is infected with a Trojan horse even though it is compiled using a C compiler whose source code (C-to-binary-compiler-in-C program) contains no code for inserting Trojan horses!

Notes:

Although only 3 pages long, the Thompson paper is very dense and challenging. Don’t be surprised if it requires multiple readings to ``get’’ the ideas, which are profound.
Double-check your derivations to make sure that they make sense and actually describe what’s being said in Thompson’s paper.

4. Static Argument Checking in Intex (12 points)

As described in the lecture slides on Intex, it is possible to statically determine (i.e., without running the program) whether an Intex program contains a argument reference with an out-of-bound index. In this problem you will flesh out skeleton implementations of the two approaches for static argument checking sketched in the slides. The skeleton implementations are in the file ps9/IntexArgChecker.sml.

Begin this problem by renaming the starter file IntexArgChecker.sml in ~/cs251/sml/ps9 to yourAccountName-IntexArgChecker.sml.

Top-down checker (6 points): In the top-down approach, the checkTopDown function on a program passes the number of arguments to the checkExpTopDown function on expressions, which recursively passes it down the subexpressions of the abstract syntax tree. When an Arg expression is reached, the index is examined to determine a boolean that indicates whether it is in bounds. The boolean on all subexpressions are combined in the upward phase of recursion to determine a boolean for the whole tree. Complete the following skeleton to flesh out this approach.
```
(* val checkTopDown: pgm -> bool *)
fun checkTopDown (Intex(numargs,body)) =
  checkExpTopDown numargs body

(* val checkExpTopDown : int -> Intex.exp -> bool *)
and checkExpTopDown numargs (Int i) = raise Unimplemented
  | checkExpTopDown numargs (Arg index) = raise Unimplemented
  | checkExpTopDown numargs (BinApp(_,exp1,exp2)) = raise Unimplemented
```
An earlier version of this problem mentioned uncommenting the definition of topDownChecks to test your implementation. This was an accidental leftover from a previous semester. The correct way to test the top-down and bottom-up checkers is described in the notes below.
Bottom-up checker (6 points): In the bottom-up approach, the checkExpBottomUp function returns a pair (min, max) of the minimum and maximum argument indices that appear in an expression. If an expression contains no argument indices, it should return the (valOf Int.maxInt, valOf Int.minInt), which is a pair of SML’s (1) maximum integer and (2) minumum integer. The functions Int.min and Int.max are useful for combining such pairs. (Note that Int.maxInt is the identity for Int.min, and Int.minInt is the identity for Int.max.)

The checkBottomUp function on programs returns true if all argument references are positive and less than or equal to the programs number of arguments, and false otherwise. Complete the following skeleton to flesh out this approach.
```
(* checkBottomUp: pgm -> bool *)
fun checkBottomUp (Intex(numargs,body)) =
  let val (min,max) = checkExpBottomUp body
   in 0 < min andalso max <= numargs
  end
   
(* val checkExpBottomUp : Intex.exp -> int * int *)
and checkExpBottomUp (Int i) = (valOf Int.maxInt, valOf Int.minInt)
  | checkExpBottomUp (Arg index) = raise Unimplemented
  | checkExpBottomUp (BinApp(_,exp1,exp2)) = raise Unimplemented
```
Notes
- To test your functions:
  - In the file IntexArgCheckerTest.sml, change the line
```
use "IntexArgChecker.sml";
```
    to
```
use "yourAccountName-IntexArgChecker.sml";
```
  - Run the file IntexArgCheckerTest.sml.
- It’s OK to use Int.min/Int.max to find the minimum and maximium of two numbers, but it’s not OK to use these to return the first/second elements of the two-tuple returned by checkExpBottomUp; instead use pattern matching! Why? Because they return the wrong value for the tuple returned for an integer. (Study the code to understand why.)

5. Static Stack Depth in the Intex-to-PostFix Compiler (21 points)

The intexToPostFix function on slide 20 of the lecture slides on Intex automatically translates an Intex program to a PostFix program that has the same meaning. The challenging part of this translation is determining the correct index to use for an Nget command when translating an Arg node in an Intext AST.

The key to solving this technical problem is to provide the expToCmds helper function with a depth argument that statically tracks the number of values that have been pushed on the PostFix stack above the argument values at any point of the computation.

The purpose of this problem is for you to study this idea in the context of a particular Intex program so that you better understand it.

(3 points) Draw the abstract syntax tree for the following Intex program, which we shall call P_Intex.
```
(intex 4 (div (add ($ 1)
                   (mul ($ 2)
                        (sub ($ 3) ($ 4))))
              (rem (sub (mul ($ 4) ($ 3))
                        ($ 2))
                   ($ 1))))
```
For drawing the Intex AST, use the conventions illustrated in slides 3 and 4 of the Intex lecture slides.

You may draw the tree by hand or use a drawing program, whichever is easier for you. This will be a wide diagram, so you’ll want to draw it in landscape mode rather than portrait mode. To save space, do not label the edges (i.e., no numargs, body, rator, rand1, rand2, index, or value labels should be used).

Since you will be annotating this tree with extra information in parts b and d, leave enough room to add some annotations to the right of each node. Here is an example of an annotated node.
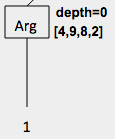
(4 points) In your AST for P_Intex from part a, annotate each expression node with the depth associated with that node when it is encountered by the expToCmds function within the intexToPostFix function. As shown above, you should write depth=d to the right of each expression node, where d is the depth of the node.
(6 points) Write down the PostFix program that is the result of translating the Intex program P_Intex from part a using the intexToPostFix function. We shall call this program P_PostFix. (You should do this translation by hand, not by running the function in SML.) Important: You translated PostFix code must be exactly the code that would be generated by the intexToPostFix function, not just a PostFix program that happens to have the same behavior. Why? Because the purpose of this problem is to understand how the intexToPostFix function (and, in particular, its depth argument) work.

Use comments to explain the commands in the translated program. Here is an example of commented PostFix code generated by translating the Intex program example (intex 4 (* (- ($ 1) ($ 2)) (/ ($ 3) ($ 4)))) from the Intex lecture slides.
```
(postfix 4 1 nget ; $1
3 nget ; $2, know that $1 on stack
sub ; (- $1 $2) 
4 nget ; $3, know that (- $1 $2) on stack
6 nget ; $4, know that $3 and (- $1 $2) on stack
div ; (/ $3 $4)
mul ; (* (- $1 $2) (/ $3 $4))
```
(8 points) Consider running P_Intex on the four arguments [4, 9, 8, 2]. In your AST for P_Intex from part a, annotate each expression node with the list of integers that corresponds to the PostFix stack that will be encountered just before the last command translated for that node by expToCmds is executed in the PostFix program P_PostFix. As shown above, you should write the stack as an SML-style list to the right of the node below the depth.

For example, below is the result of annotating the Intex AST for (intex 4 (* (- ($ 1) ($ 2)) (/ ($ 3) ($ 4)))) with depth information and the stack before executing each node when the program is given the arguments [15, 8, 30, 5].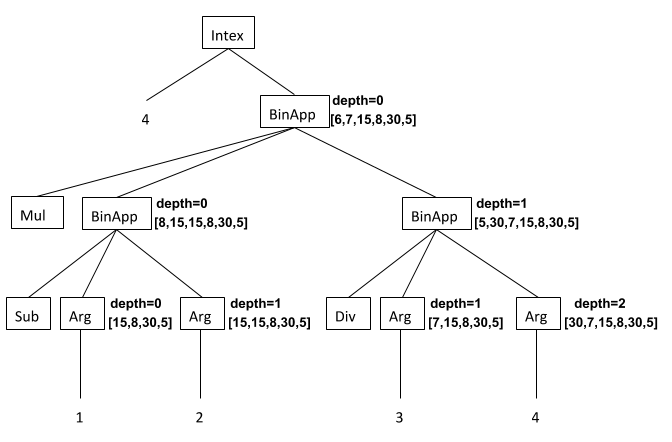

Some things to observe:
- At each Arg node in the program, the PostFix stack index of that argument in the stack annotating the node is the Arg index value plus the depth annotating the node. In particular:
  - The Arg node with index 1 has depth 0, and so translates to 1 nget.
  - The Arg node with index 2 has depth 1, and so translates to 3 nget.
  - The Arg node with index 3 has depth 1, and so translates to 4 nget.
  - The Arg node with index 4 has depth 2, and so translates to 6 nget.
- Only Intex expression nodes (BinApp and Arg nodes in this example) have annotations. The binop nodes Sub, Div, and Mul are not annotated, nor are the Arg index values or the top-level Intex program node.
- Here's an explanation of the stack annotations on the Intex AST nodes in the example:
  1. Execution of the translated program begins with the translation of the Arg node with index 1 to 1 nget. Before these commands are executed, the stack just contains the four argument values: [15, 8, 30, 5]. The result of executing the PostFix code for this node is [15, 15, 8, 30, 5]. The fact that the value of the left operand of Sub has been pushed on the stack causes the depth to increment from 0 to 1 for the right operand.
  2. The translated program executes the translation of the Arg node with index 2, which is 3 nget. Before these commands are executed, the stack contains the result of executing the PostFix code in Step 1, so the stack is [15, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [8, 15, 15, 8, 30, 5].
  3. The translated program performs the sub command translated for the end of the code for the Sub BinApp node. Before the subtraction is performed, the stack is the result of executing the PostFix code in Step 2, so the stack is [8, 15, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [7, 15, 8, 30, 5]. Since two stack values were popped but one was pushed when executing sub. So the depth for the next step (the division BinApp) is still 1.
  4. The translated program executes the translation of the Arg node with index 3, which is 4 nget. Before these commands are executed, the stack contains the result of executing the PostFix code in Step 3, so the stack is [7, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [30, 7, 15, 8, 30, 5]. Pushing the left operand of the Div BinApp increments the depth from 1 to 2 for its right operand.
  5. The translated program executes the translation of the Arg node with index 4, which is 6 nget. Before these commands are executed, the stack contains the result of executing the PostFix code in Step 4, so the stack is [30, 7, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [5, 30, 7, 15, 8, 30, 5].
  6. The translated program performs the div command translated for the end of the code for the Div BinApp node. Before the divistion is performed, the stack is the result of executing the PostFix code in Step 5, so the stack is [5, 30, 7, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [6, 7, 15, 8, 30, 5].
  7. The translated program performs the mul command translated for the end of the code for the Mul BinApp node. Before the multiplication is performed, the stack is the result of executing the PostFix code in Step 6, so the stack is [6, 7, 15, 8, 30, 5]. The result of executing the PostFix code for this node is [42, 15, 8, 30, 5]. This stack is not shown in the annotated tree, but is the final stack for the program (which returns the result value 42). </ol> </ul>

Extra Credit: Self-printing Program (15 points)

In his Turing-lecture-turned-short-paper Reflections on Trusting Trust, Ken Thompson notes that it is an interesting puzzle to write a program in a language whose effect is to print out a copy of the program. We will call this a self-printing program. Write a self-printing program in any general-purpose programming language you choose. Your program should be self-contained — it should not read anything from the file system.

Important Note: There are lots of answers on the Internet, but you will get zero points if you just copy one of those. (I can tell!) Write this program from scratch completely on your own, without looking anything up online.