PS8: Set Yourself Free
- Dueish: Mon. Apr. 22, 2019
- Notes:
- This pset has 100 total points.
- This pset contains one solo problems worth 20 points.
- It has three regular problems worth 80 points on SML programming:
- The first SML problem (Problem 2) requires lecture material on sum-of-product (SOP) datatypes slides with solutions here, which has already been covered. After finishing the PS7 Problem 3 SML problem on translating Racket functions into SML, PS8 Problem PS8 Problem 2 on 2-3 Trees should become you new high-priority problem. This should have a higher priority than any other undone work in 251. This will give you valuable practice with sum-of-product datatypes that you will need to understand SML programs going forward.
- The other two SML problems (Problems 3 and 4) are based on lecture material on modules and abstract datatypes that will be covered in class on Thu. Apr. 11 and Wed. Apr. 17. You should be able to start these problem after lecture on Wed. Apr. 17. On Wed. Apr. 17, PS8 Problems 3 and 4 will become your newest high-priority problems.
-
Times from Spring ‘18 (in hours, n=26)
Times Problem 1 Problem 2 Problem 3 Problem 4 average time (hours) 2.0 3.5 2.3 3.1 median time (hours) 1.5 3.0 2.0 3.0 25% took more than 2.4 4.0 2.9 3.9 10% took more than 3.8 5.0 3.3 5.0 - Submission:
- In your yourFullName CS251 Spring 2019 Folder, create a Google Doc named yourFullName CS251 PS8.
- At the top of your yourFullName CS251 PS8 doc, include your name, problem set number, date of submission, and an approximation of how long each problem part took.
- For all parts of all problems, include all answers (including SML code) in your PS8 google doc. Format code using a fixed-width font, like Consolas or Courier New. You can use a small font size if that helps.
- Don’t forget to include all non-code answers:
- The box-and-pointer-diagram in Problem 1b.
- The explanations of unimplementable
FunSetfunctions in Problem 3b.
- You will create the following code files from starter files populating your
~/cs251/sml/ps8directory on yourcsenv/wxVirtual Machine:- Problem 1:
yourAccountName-partialReverses.sml - Problem 2:
yourAccountName-TTTreeFuns.sml - Problem 3:
yourAccountName-FunSet.sml - Problem 4:
yourAccountName-OperationTreeSet.sml
For these problems:
- include all functions from the four files named
yourAccountName...in your Google Doc (so that I can comment on them). -
Drop a copy of your
~/cs251/sml/ps8folder in your~/cs251/drop/ps08drop folder oncs.wellesley.eduby executing the following (replacing both occurrences ofgdomeby your cs server username):scp -r ~/cs251/sml/ps8 gdome@cs.wellesley.edu:/students/gdome/cs251/drop/ps08
- Problem 1:
Starting this Problem Set
All four problems involve starter files in the ~/cs251/sml/ps8 directory in your csenv/wx Virtual Machine.
To create this directory, follow the git instructions in this doc
REMINDER: ALWAYS MAKE A BACKUP OF YOUR .sml FILES AT THE END OF EACH DAY TO AVOID POTENTIAL LOSS OF WORK.
1. Solo Problem: Partial Reverses (20 points)
This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.
-
(5 points) Consider the following
partial-reversesfunction in Racket. Draw a box-and-pointer diagram of the list that results from the invocation(partial-reverses '(1 2 3 4)). Use the style of diagram shown in PS3 Problem 2. Study the code carefully and be sure to accurately show all sharing between cons cells in your diagram.(define (partial-reverses xs) (define (partial-reverses-tail ys rev list-rev) (if (null? ys) (cons rev list-rev) (partial-reverses-tail (rest ys) (cons (first ys) rev) (cons rev list-rev) ))) (partial-reverses-tail xs '() '()))Note: As an example of sharing in box-and-pointer diagrams, consider
(define numList '(7 2 4)) (define listOfNumLists (list (append numList (rest numList)) numList (rest numList)))The result has 9 cons cells arranged as follows:
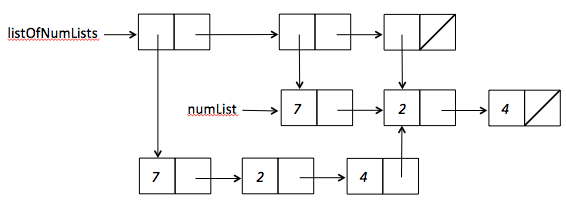
However, if we just enter the printed representation
'((7 2 4 2 4) (7 2 4) (2 4))forlistOfNumLists, that would create 13 cons cells: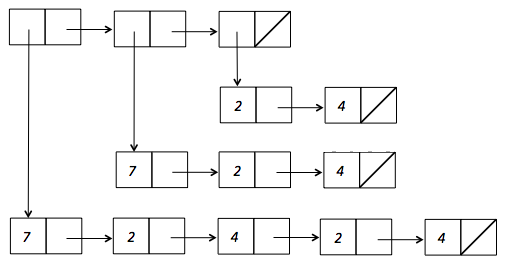
-
(2 points) How many cons cells would there be in the result of
(partial-reverses (range 1 1001))? -
(5 points) Make a copy of the starter file
partialReverses.smlnamedyourAccountName-partialReverses.sml. InyourAccountName-partialReverses.sml, translate the Racket definition ofpartial-reversesinto an SML functionpartialReversesthat has exactly the same behavior (in terms of generating lists with the same sharing).Similar to the
partial-reversesfunction in Racket, the SMLpartialReversesfunction should have a nested function definitionpartialReversesTailthat is called within it.As in PS7 Problem 1, in this and the following subproblems of this solo task, do not use
#1,#2, etc. to extract tuple components orList.hd,List.tl, orList.nullto decompose and test lists. Instead, use pattern matching on tuples and lists. -
(4 points) In
yourAccountName-partialReverses.sml, flesh out the following SML skeleton definition ofpartialReversesIterateso that it usesiterateto iteratively calculate the same result (including sharing) aspartialReverses:fun partialReversesIterate xs = iterate (* expression1 *) (* expression2 *) (* expression3 *) (xs, [], [])yourAccountName-partialReverses.smlincludes this definition ofiterate(from PS7 Problem 3b):(* val iterate = fn : ('a -> 'a) -> ('a -> bool) -> ('a -> 'b) -> 'a -> 'b *) fun iterate next isDone finalize state = if isDone state then finalize state else iterate next isDone finalize (next state)Notes:
-
In
yourAccountName-partialReverses.sml, the definition ofiteratemust appear above the defintion ofpartialReversesIterate, which uses it. -
You can use
= []to test for an empty list.
-
-
(4 Points) In
yourAccountName-partialReverses.sml, flesh out the following skeleton definition ofpartialReversesFoldlso that it usesfoldlto iteratively calculate the same result (including sharing) aspartialReverses:fun partialReversesFoldl xs = foldl (* expression1 *) (* expression1 *) xsRecall that SML’s
foldlfunction has type('a * 'b -> 'b) -> 'b -> 'a list -> 'b.
2. 2-3 Trees (30 points)
In this problem you will use SML to implement aspects of 2-3 trees, a particular search tree data structure that is guaranteed to be balanced.
Begin by skimming pages 1 through 7 of this handout on 2-3 trees. (I created this handout for CS230 in Fall, 2004, but we no longer teach 2-3 trees in that course).
In a 2-3 tree, there are three kinds of nodes: leaves, 2-nodes, and 3-nodes. Together, these can be expressed in SML as follows:
datatype TTTree = (* 2-3 tree of ints *)
L (* Leaf *)
| W of TTTree * int * TTTree (* tWo node *)
| H of TTTree * int * TTTree * int * TTTree (* tHree node *)For simplicity, we will only consider 2-3 trees of integers, though they can be generalized to handle any type of value.
For conciseness in constructing and displaying large trees, the three constructors have single-letter names. For example, below are the pictures of four sample 2-3 trees from the handout and how they would be expressed with these constructors:
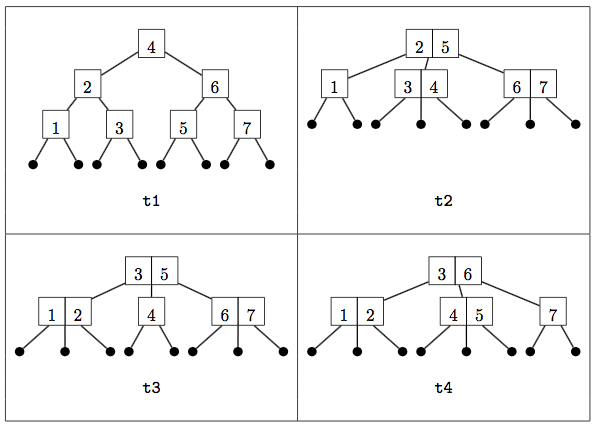
val t1 = W( W(W(L,1,L), 2, W(L,3,L)), 4, W(W(L,5,L), 6, W(L,7,L)))
val t2 = H( W(L,1,L), 2, H(L,3,L,4,L), 5, H(L,6,L,7,L))
val t3 = H( H(L,1,L,2,L), 3, W(L,4,L), 5, H(L,6,L,7,L))
val t4 = H( H(L,1,L,2,L), 3, H(L,4,L,5,L), 6, W(L,7,L))As explained in the handout on 2-3 trees, a 2-3 tree is only valid it it satisfies two additional properties:
- The ordering property:
- In a 2-node with left subtree l, value X, and right subtree r, (all values in l) ≤ X ≤ (all values in r).
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, (all values in l) ≤ X ≤ (all values in m) ≤ Y ≤ (all values in r).
- The height property (called path length invariant in the handout): in a 2-node or 3-node, the height of all subtrees must be exactly the same.
The height property guarantees that a valid 2-3 tree is balanced. Together, these two properties guarantee that a 2-3 tree is efficiently searchable.
Your ~/cs251/sml/ps8 folder includes the file TTTree.sml, which contains the TTTree dataytype defined above as well as numerous examples of valid and invalid 2-3 trees that are instances of this datatype. Note that t and vt are used for valid trees, io is used for invalidly ordered trees, and ih is used for invalid height trees.
| tree name | elements | ordered? | satisfies the height property? |
|---|---|---|---|
| t1 | [1,…,7] | Yes | Yes, with height 3 |
| t2 | [1,…,7] | Yes | Yes, with height 2 |
| t3 | [1,…,7] | Yes | Yes, with height 2 |
| t4 | [1,…,7] | Yes | Yes, with height 2 |
| vt0 | [] | Yes | Yes, with height 0 |
| vt2 | [1,2] | Yes | Yes, with height 1 |
| vt17 | [1,…,17] | Yes | Yes, with height 3 |
| vt20 | [1,…,20] | Yes | Yes, with height 4 |
| vt44 | [1,…,44] | Yes | Yes, with height 5 |
| vt92 | [1,…,92] | Yes | Yes, with height 6 |
| io2 | [1,2] | No | Yes, with height 1 |
| io7 | [1,…,7] | No | Yes, with height 2 |
| io17 | [1,…,17] | No | Yes, with height 3 |
| io20 | [1,…,20] | No | Yes, with height 4 |
| io44 | [1,…,44] | No | Yes, with height 5 |
| io92 | [1,…,92] | No | Yes, with height 6 |
| ih2 | [1,2] | Yes | No |
| ih7 | [1,…,7] | Yes | No |
| ih17 | [1,…,17] | Yes | No |
| ih20 | [1,…,20] | Yes | No |
| ih44 | [1,…,44] | Yes | No |
| ih92 | [1,…,92] | Yes | No |
These trees are used to define two lists:
val validTrees = [vt0, vt2, t2, t3, t4, t1, vt17, vt20, vt44, vt92]
val invalidTrees = [io2, io7, io17, io20, io44, io92,
ih2, ih9, ih17, ih20, ih44, ih92]In this problem you will (1) implement a validity test for 2-3 trees and (2) implement the effcient 2-3 insertion algorithm from the handout on 2-3 trees.
Your ~/cs251/sml/ps8 folder also includes the starter file TTTreeFuns.sml. In this file, flesh out the missing definitions as specified below. When you finish this problem, rename the file to yourAccountName-TTTreeFuns.sml before you submit it.
Be sure to perform execute the following in a shell in your csenv/wx appliance to get the ~/cs251/sml/ps8 folder:
cd ~/cs251/sml
git pull origin master-
satisfiesOrderingProperty(7 points)In this part, you will implement a function
satisfiesOrderingProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree ordering property andfalseif it does not. An easy way to do this is to define two helper functions:elts: TTTree -> int listreturns a list of all the elements of the tree in in-order — i.e.,- In a 2-node with left subtree l, value X, and right subtree r, all values in l are listed before X, which is listed before all elements in r.
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, all values in l are listed before X, which is listed before all values in m, which are listed before Y , which is listed before all values in r.
isSorted: int list -> boolreturnstrueif the list of integers is in sorted order andfalseotherwise.
For example:
- elts vt17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] : int list - elts io17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,17,16] : int list - isSorted(elts vt17); val it = true : bool - isSorted(elts io17); val it = false : boolUsing these two helper functions,
satisfiesOrderingPropertycan be implemented as:fun satisfiesOrderingProperty t = isSorted(elts t)For example:
- map satisfiesOrderingProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesOrderingProperty invalidTrees; val it = [false,false,false,false,false,false,true,true,true,true,true,true] : bool listNotes:
-
It is assumed that you are already familiar with running SML in Emacs from PS7 Problem 3.
-
Your workflow on this problem should be as follows:
-
Once (and only once), load the
TTTree.smlfile into an SML interpreter to load theTTTreedatatype and example trees.-
If you’re running SML in Emacs in a
csenvorwxappliance (recommended), you can loadTTTree.smlvia these steps:-
Open
~/cs251/sml/ps8/TTTree.smlin Emacs: use theC-x C-fkeyboard shortcut or the menu itemFile>Open File) -
Load
TTTree.smlfile into a*sml*interpreter buffer: use theC-c C-bkeyboard shortcut (followed by areturnif prompted in the mini-buffer at the bottom of the screen) or the menu itemSML>Process>Send Buffer. You may need to scroll down in the*sml*buffer to see what has been loaded.
-
-
Otherwise, in an SML interpreter, do the following:
- Posix.FileSys.chdir "~/cs251/sml/ps8"; val it = () : unit - use "TTTree.sml"; ... lots of printout omitted ...Note that
Posix.FileSys.chdirneeds to be called only once for an interactive session.
-
-
Now open the file
TTTreeFuns.smland edit some definitions -
Every time you change the file
TTTreeFuns.smland want to test your changes in the SML interpreter, load this file into the interpreter using one of the two approaches described in Step 1.
-
-
You may need to execute
Control.Print.printLength := 100;in order to see all the list elements. -
Implement
isSortedusing the same zipping approach you used in PS4. As seen in Problem 2b, you do zipping in SML viaListPair.zipfrom the ListPair module.List.allfrom the List module is also helpful.
-
satisfiesHeightProperty(9 points)In this part, you will implement a function
satisfiesHeightProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree height property andfalseif it does not. An easy way to do this is to definesatisfiesHeightPropertyasfun satisfiesHeightProperty t = Option.isSome (height t)where
Option.isSomeis a function from the Option module that determines if anoptionvalue is aSOME(vs. aNONE) andheightis a function with typeTTTree -> option intsuch thatheight treturnsSOME hiftsatisfies the height property with heighthand otherwise returnsNONE.Implement the
heightfunction by fleshing out this skeleton:(* height: TTTree -> int option *) fun height L = (* return an appropriate option value here *) | height (W(l, _, r)) = (case (height(l), height(r)) of (* put appropriate pattern clauses here *)) | (* handle the H case here, similarly to the W case *)For example:
- map height validTrees; val it = [SOME 0,SOME 1,SOME 2,SOME 2,SOME 2,SOME 3,SOME 3,SOME 4,SOME 5,SOME 6] : int option list - map height invalidTrees; val it = [SOME 1,SOME 2,SOME 3,SOME 4,SOME 5,SOME 6,NONE,NONE,NONE,NONE,NONE,NONE] : int option listNotes:
-
It’s important to enclose the
caseexpressions withinheightin parens to distinguish the pattern clauses of thecaseexpression from those of theheightfunction definition. -
You should not exhaustively match patterns for four combinations of
SOME/NONEfor a two-node and nine combinations for a three-node. Instead use the underscore pattern_to match “everything else”. With the underscore, only two patterns are necessary for handling two-nodes and two patterns are necessary for handling three-nodes. -
Once
heightis defined,satisfiesHeightPropertyis defined:- map satisfiesHeightProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesHeightProperty invalidTrees; val it = [true,true,true,true,true,true, false,false,false,false,false,false] : bool list -
Once both
satisfiesOrderingPropertyandsatisfiesHeightPropertyare defined, it is trivial to define a functionisValid: TTTree -> boolthat returnstrueif a given 2-3 tree is valid andfalseotherwise.fun isValid t = satisfiesOrderingProperty t andalso satisfiesHeightProperty t - map isValid validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map isValid invalidTrees; val it = [false,false,false,false,false,false, false,false,false,false,false,false] : bool list
-
-
insert(14 points) In this part, you will implement the insertion algorithm for 2-3 trees as described on pages 3 to 5 of the handout on 2-3 trees. You will not implement the special cases described on page 6 .The insertion algorithm is a recursive algorithm that uses the notion of a pseudo 2-node that is “kicked up” in certain cases and handled specially in the upward phase of the recursion. To distinguish an insertion result that is a regular 2-3 tree from a pseudo 2-node that is “kicked up”, we use the following datatype:
datatype InsResult = Tree of TTTree | KickedUp of TTTree * int * TTTree (* pseudo 2-node "kicked up" from below *)You will implement 2-3 tree insertion via a pair of functions:
-
(insert v t)returns the newTTTreethat results from inserting a given intvinto a given treet.inserthas typeint -> TTTree -> TTTree. -
(ins v t)is a helper function that returns the instance ofInsResultthat results from inserting a given intvinto a given treet.inshas typeint -> TTTree -> InsResult.
Your implementation should flesh out the following code skeleton by turning the pictures on pages 3 to 5 from the handout on 2-3 trees into SML code.
(* insert: int -> TTTree -> TTTree *) fun insert v t = case ins v t of Tree t => t | KickedUp(l, w, r) => W(l, w, r) and (* "and" glues together mutually recursive functions *) (* ins: int -> TTTree -> InsResult *) ins v L = KickedUp (L, v, L) | ins v (W(l, X, r)) = if v <= X then (case ins v l of Tree l' => Tree(W(l', X, r)) | KickedUp (l', w, m) => Tree(H(l', w, m, X, r))) else (* flesh this out *) | (* handle an H node similarly to the W node based on rules from the handout *)Notes:
-
The
insfunction should only callinsrecursively and should not callinsert. -
An easy way to test
insertis to use thetestInsertfunction defined at the end of the starter file.fun listToTTTree xs = foldl (fn (x,t) => insert x t) L xs fun range lo hi = if lo >= hi then [] else lo :: (range (lo + 1) hi) fun testInsert numVals = let val inputs = range 0 numVals val ttt = listToTTTree inputs val _ = if isValid ttt then print "Tree is valid.\n" else print "***TEST FAILED: Tree is invalid!\n" val _ = if elts ttt = inputs then print "Tree contains all inputs in expected order.\n" else print "***TEST FAILED: Tree elements are not what is expected!\n" in ttt endGiven a nonnegative integer n,
testInsertcreates a 2-3 tree by inserting the integers from 0 up to (but not including) n in an initially empty tree. It also checks that the resulting tree is valid and contains exactly the expected numbers.- testInsert 5; Tree is valid. Tree contains all inputs in expected order. val it = H (W (L,0,L),1,W (L,2,L),3,W (L,4,L)) : TTTree - testInsert 10; Tree is valid. Tree contains all inputs in expected order. val it = W (W (W #,1,W #),3,H (W #,5,W #,7,H #)) : TTTreeBy default, SML uses the
#character to hide tree details below a default depth of 5. You can set this depth to be higher as shown below:- Control.Print.printDepth := 100; val it = () : unit - testInsert 10; Tree is valid. Tree contains all inputs in expected order. val it = W (W (W (L,0,L),1,W (L,2,L)),3,H (W (L,4,L),5,W (L,6,L),7,H (L,8,L,9,L))) : TTTree - testInsert 50; Tree is valid. Tree contains all inputs in expected order. val it = H (W (W (W (W (L,0,L),1,W (L,2,L)),3,W (W (L,4,L),5,W (L,6,L))),7, W (W (W (L,8,L),9,W (L,10,L)),11,W (W (L,12,L),13,W (L,14,L)))),15, W (W (W (W (L,16,L),17,W (L,18,L)),19,W (W (L,20,L),21,W (L,22,L))),23, W (W (W (L,24,L),25,W (L,26,L)),27,W (W (L,28,L),29,W (L,30,L)))),31, W (W (W (W (L,32,L),33,W (L,34,L)),35,W (W (L,36,L),37,W (L,38,L))),39, W (W (W (L,40,L),41,W (L,42,L)),43, H (W (L,44,L),45,W (L,46,L),47,H (L,48,L,49,L))))) : TTTreetestInsertcan find some bugs in yourinsertfunction. Here’s an example where it reports a tree that is invalid because its left subtree has height 1 while its right subtree has height 2:- testInsert 5; ***TEST FAILED: Tree is invalid! Tree contains all inputs in expected order. val it = W (W (L,0,L),1,W (W (L,2,L),3,W (L,4,L))) : TTTree -
Unfortunately, inserting elements in sequential order as above tends to create 2-3 trees with almost all 2-nodes and very few 3-nodes, so it can easily miss bugs in your insertion cases that involve 3-nodes.
It turns out a better way to test
insertis to insert integers in a range that have been “shuffled” in various ways, which gives a better distribution of 2-nodes and 3-nodes, and is more likely to catch bugs in yourinsertfunction. This approach to testing is implemented in the separate fileTTTreeFunsTest.sml, which will test yourinsertfunction on thousands of test cases.Before using the file
TTTreeFunsTest.sml, open it in an editor and change the lineuse "TTTreeFuns.sml"; (* Student solutions *)to
use "yourAccountName-TTTreeFuns.sml"; (* Student solutions *)Then send the contents of this modified file to
*sml*` buffer. If you do this, the final values will look like the following when yourinsertfunction passes all the test cases::val testInsertUpToSize5 = ("Passed all 8 test cases",[]) : string * (int list * TTTree) list val testInsertUpToSize10 = ("Passed all 28 test cases",[]) : string * (int list * TTTree) list val testInsertUpToSize25 = ("Passed all 172 test cases",[]) : string * (int list * TTTree) list val testInsertUpToSize50 = ("Passed all 613 test cases",[]) : string * (int list * TTTree) list val testInsertUpToSize100 = ("Passed all 2152 test cases",[]) : string * (int list * TTTree) list val it = () : unitIf there are test cases that fail, a list of up to 10 input/output cases where the output tree is incorrect will be shown. For example:
val testInsertUpToSize5 = ("FAILED TEST CASES: invalid trees in these input/output pairs", [([0,1,2,3,4],W (W (L,0,L),1,W (W (L,2,L),3,W (L,4,L)))), ([0,1,3,2,4],W (W (L,0,L),1,W (W (L,2,L),3,W (L,4,L))))]) : string * (int list * TTTree) list
-
3. Fun Sets (20 points)
In SML, we can implement abstract data types in terms of familiar structures like lists and trees. But we can also use functions to implement data types. In this problem, you will investigate a compelling example of using functions to implement sets.
Your ~/cs251/sml/ps8 folder contains the starter file FunSet.sml. This includes the same SET signature we studied in class:
signature SET =
sig
(* The type of sets *)
type ''a t
(* An empty set *)
val empty : ''a t
(* Construct a single-element set from that element. *)
val singleton : ''a -> ''a t
(* Check if a set is empty. *)
val isEmpty : ''a t -> bool
(* Return the number of elements in the set. *)
val size : ''a t -> int
(* Check if a given element is a member of the given set. *)
val member : ''a -> ''a t -> bool
(* Construct a set containing the given element and all elements
of the given set. *)
val insert : ''a -> ''a t -> ''a t
(* Construct a set containing all elements of the given set
except for the given element. *)
val delete : ''a -> ''a t -> ''a t
(* Construct the union of two sets. *)
val union : ''a t -> ''a t -> ''a t
(* Construct the intersection of two sets. *)
val intersection : ''a t -> ''a t -> ''a t
(* Construct the difference of two sets
(all elements in the first set but not in the second.) *)
val difference : ''a t -> ''a t -> ''a t
(* Construct a set from a list of elements.
Do not assume the list elements are unique. *)
val fromList : ''a list -> ''a t
(* Convert a set to a list without duplicates.
The elements in the resulting list may be in any order. *)
val toList : ''a t -> ''a list
(* Construct a set from a predicate function:
the resulting set should contain all elements for which
this predicate function returns true.
This acts like math notation for sets. For example:
{ x | x mod 3 = 0 }
would be written:
fromPred (fn x => x mod 3 = 0)
*)
val fromPred : (''a -> bool) -> ''a t
(* Convert a set to a predicate function. *)
val toPred : ''a t -> ''a -> bool
(* Convert a set to a string representation, given a function
that converts a set element into a string representation. *)
val toString : (''a -> string) -> ''a t -> string
(* Convert a set to a list without duplicates.
The elements in the resulting list may be in any order. *)
val toList : ''a t -> ''a list
(* Construct a set from a predicate function:
the resulting set should contain all elements for which
this predicate function returns true.
This acts like math notation for sets. For example:
{ x | x mod 3 = 0 }
would be written:
fromPred (fn x => x mod 3 = 0)
*)
val fromPred : (''a -> bool) -> ''a t
(* Convert a set to a predicate function. *)
val toPred : ''a t -> ''a -> bool
(* Convert a set to a string representation, given a function
that converts a set element into a string representation. *)
val toString : (''a -> string) -> ''a t -> string
endBegin this problem by making a copy of FunSet.sml named yourAccountName-FunSet.sml. Make all your edits to yourAccountName-FunSet.sml and not to FunSet.sml.
exception Unimplemented (* Placeholder during development. *)
exception Unimplementable (* Impossible to implement *)
(* Implement a SET ADT using predicates to represent sets. *)
structure FunSet :> SET = struct
(* Sets are represented by predicates. *)
type ''a t = ''a -> bool
(* The empty set is a predicate that always returns false. *)
val empty = fn _ => false
(* The singleton set is a predicate that returns true for exactly one element *)
fun singleton x = fn y => x=y
(* Determining membership is trivial with a predicate *)
fun member x pred = pred x
(* complete this structure by replacing "raise Unimplemented"
with implementations of each function. Many of the functions
*cannot* be implemented; for those, use raise Unimplementable
as there implementation *)
fun isEmpty _ = raise Unimplemented
fun size _ = raise Unimplemented
fun member _ = raise Unimplemented
fun insert _ = raise Unimplemented
fun delete _ = raise Unimplemented
fun union _ = raise Unimplemented
fun intersection _ = raise Unimplemented
fun difference _ = raise Unimplemented
fun fromList _ = raise Unimplemented
fun toList _ = raise Unimplemented
fun fromPred _ = raise Unimplemented
fun toPred _ = raise Unimplemented
fun toString _ = raise Unimplemented
endThe fromPred and toPred operations are based on the observation that a membership predicate describes exactly which elements are in the set and which are not. Consider the following example:
- val s235 = fromPred (fn x => (x = 2) orelse (x = 3) orelse (x = 5));
val s235 = - : int t
- member 2 s235;
val it = true : bool
- member 3 s235;
val it = true : bool
- member 5 s235;
val it = true : bool
- member 4 s235;
val it = false : bool
- member 100 s235;
val it = false : boolThe set s235 consists of exactly those elements satisfying the predicate passed to fromPred – in this case, the integers 2, 3, and 5.
Defining sets in terms of predicates has many benefits. Most important, it is easy to specify sets that have infinite numbers of elements! For example, the set of all even integers can be expressed as:
fromPred (fn x => (x mod 2) = 0)This predicate is true of even integers, but is false for all other integers. The set of all values of a given type is expressed as fromPred (fn x => true). Many large finite sets are also easy to specify. For example, the set of all integers between 251 and 6821 (inclusive) can be expressed as
fromPred (fn x => (x >= 251) andalso (x <= 6821))Although defining sets in terms of membership predicates is elegant and has many benefits, it has some big downsides. The biggest one is that several functions in the SET signature simply cannot be implemented. You will explore this downside in this problem.
-
(16 points) Flesh out the code skeleton for the
FunSetstructure inyourAccountName-FunSet.sml. Some value bindings cannot be implemented; for these, useraise Unimplementableas the implementation.Notes:
-
The notion that a set can be implemented as a predicate function is a mind-blowing example of the power of using functions to implement data structures!
-
In this set implementation, the only function in which list operations make sense is in
fromList. It is an error to use list operations elsewhere. -
Since a predicate is a function of one argument that returns a boolean, when returning a set-as-predicate, it is always sensible to use an expression of the form
fn y =>boolexp, where y is the candidate element being tested for membership, and boolexp is a boolean-valued expression indicating whetheryis in the set. -
Various tests of the
FunSetimplementation are performed in the separate fileFunSetTest.sml. If you open that file, change the lineuse "FunSet.sml";touse "yourAccountName-FunSet.sml";, and send its contents to the*sml*buffer, it will define atestResultsvalue that summarizes the results of 14 test cases as a list of strings. If it passes all 14 test cases, the next-to-last line will be:val testResults = ["Passed all 14 test cases:"] : string listIf some test cases fail, this will be indicated in the list of strings in the value of
testResults. For example:val testResults = ["------------------------------------------------------------", "Passed 13 test cases:","smallSet","smallerSet","mod2Set","mod3Set", "mod2SetIntersectionMod3Set","mod2SetDifferenceMod3Set", "mod3SetDifferenceMod2Set","mod3SetDifferenceMod2Set","lowSet","middleSet", "highSet","bigIntersection","bigDifference", "------------------------------------------------------------", "Failed 1 test case:","mod2SetUnionMod3Set:", "expected = [0,2,3,4,6,8,9,10,12,14,15,16,18,20,21,22,24,26,27,28,30,32,33,34,36,38,39,40,42,44,45,46,48,50,51,52,54,56,57,58\ ,60,62,63,64,66,68,69,70,72,74,75,76,78,80,81,82,84,86,87,88,90,92,93,94,96,98,99,100]", " actual = [0,6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96]", "------------------------------------------------------------"] : string list
-
-
(4 points) For each function that you declared being unimplementable, explain in English why it is unimplementable. Give concrete examples where appropriate.
4. Operation Tree Sets (30 points)
A very different way of representing a set as a tree is to use a sum-of-products data structure to remember the structure of the set operations empty, insert, delete, union, intersection, and difference used to create the set. For example, consider the set s created as follows:
val s = (delete 4 (difference (union (union (insert 1 empty)
(insert 4 empty))
(union (insert 7 empty)
(insert 4 empty)))
(intersection (insert 1 empty)
(union (insert 1 empty)
(insert 6 empty)))))Abstractly, s is the singleton set {7}. But one concrete representation of s is the following operation tree:
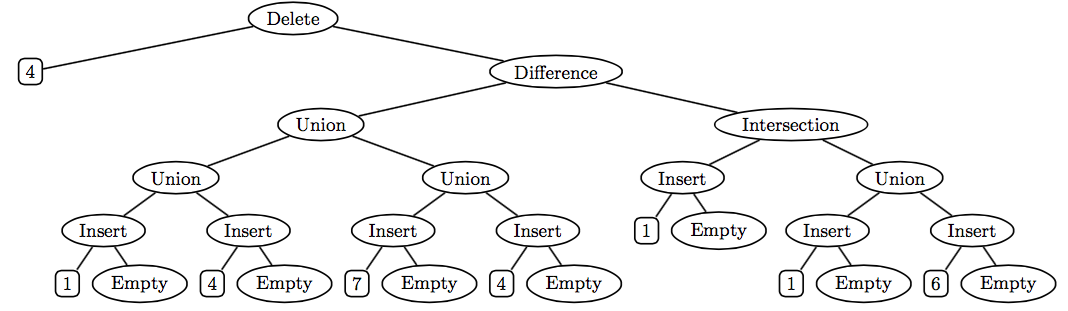
One advantage of using such operation trees to represent sets is that the empty, insert, delete, union, difference, and intersection operations are extremely cheap — they just create a new tree node with the operands as subtrees, and thus take constant time and space! But other operations, such as member and toList, can be more expensive than in other implementations.
In this problem, you are asked to flesh out the missing operations in the skeleton of the OperationTreeSet structure shown below. Your ~/cs251/sml/ps8 folder contains the starter file OperationTreeSet.sml.
Begin this problem by making a copy of OperationTreeSet.sml named yourAccountName-OperationTreeSet.sml. Make all your edits to yourAccountName-OperationTreeSet.sml and not to OperationTreeSet.sml.
structure OperationTreeSet :> SET = struct
datatype ''a t = Empty
| Insert of ''a * ''a t
| Delete of ''a * ''a t
| Union of ''a t * ''a t
| Intersection of ''a t * ''a t
| Difference of ''a t * ''a t
val empty = Empty
fun insert x s = Insert(x,s)
fun singleton x = Insert(x, Empty)
fun delete x s = Delete(x, s)
fun union s1 s2 = Union(s1,s2)
fun intersection s1 s2 = Intersection(s1,s2)
fun difference s1 s2 = Difference(s1,s2)
fun member _ _ = raise Unimplemented
fun toList _ = raise Unimplemented
fun isEmpty _ = raise Unimplemented
fun size _ = raise Unimplemented
fun toPred _ = raise Unimplemented
fun toString eltToString _ = raise Unimplemented
fun fromList _ = raise Unimplemented
fun fromPred _ = raise Unimplementable
endIn the OperationTreeSet structure, the set datatype t is create by constructors Empty, Insert, Delete, Union, Intersection, and Difference. The empty, singleton, insert, delete, union, intersection, difference operations are easy and have been implemented for you. You are responsible for fleshing out the definitions of the member, toList, size, isEmpty, toPred, toString, and fromList operations.
Notes:
-
Your implementation of
membershould not use thetoListfunction. Instead, it should be defined by case analysis on the structure of the operation tree. -
For the
toListfunction:-
toListshould also be defined by case analysis on the structure of the operation tree. -
The
memberfunction should not be used in the implementation oftoList(because it can be very inefficient). Instead, useList.existsandList.filterin a manner similar to the way we implemented sets as lists without duplicates in class. -
Keep in mind that sets are unordered. So your
toListfunction may return lists of elements in any order, but it should not have any duplicates. -
In your
toListdefinition, be very careful with includingtoListinside functional arguments, because this can often cause the same list to be calculated a tremendous number of times, leading to tests that take a very long time for large sets. If some of the test cases for large sets don’t return in a reasonable time, this is probably the cause. You can avoid this by using SML’slet/in/endto name the result of calculatingtoListand using the name multiple times.
-
-
Your implementation of
sizeandisEmptyshould use thetoListfunction. Indeed, it is difficult to implement these functions by a direct case analysis on the operation tree. Note thatsizewill only work correcty if the output oftoListdoes not contain duplicates. -
In the implementation of
toString, the functionString.concatWithis particularly useful. -
In the implementation of
fromList, for lists with >= 2 elements, you should first split the list into two (nearly) equal-length sublists usingList.takeandList.dropand union the results of turning the sublists into sets. This yields a height-balanced operation tree. -
Various tests of the
OperationTreeSetimplementation are performed in the separate fileOperationTreeSetTest.sml. If you open that file, change the lineuse "OperationTreeSet.sml";touse "yourAccountName-OperationTreeSet.sml";, and send its contents to the*smlbuffer, it will (among other things) perform 216 tests that are organized by groups, and will print out information about each test. The very last line will be a summary. If you seePassed all 216 teststhen you needn’t dig deeper. But if you see a message like
***FAILED 20 tests; passed 196 teststhen you should scroll back through the printout to find the test case(s) that misbehaved. For example, you might see:
s1DifferenceS2: ***Failed! actual: [19,57,97] expected: [19] s2DifferenceS1: ***FAILED! actual: [19,57,97] expected: [57,97] intersectionSmallDiffs: ***FAILED! actual: [19,57,97] expected: [] smallDelete: passed!To understand why the
expectedresult was expected, you need to study the test cases inOperationTreeSetTest.sml. -
The testing code for most functions (all except for
member) assumes thattoListworks correctly. So you must implementtoListfor for most of the tests to work.
Extra Credit 1: 2-3 Tree Deletion (20 points)
In SML, implement and test the 2-3 tree deletion algorithm presented in pages 8 through 11 of the handout on 2-3 trees.
Extra Credit 2: 2-3 Trees in Java (35 points)
Implement and test 2-3 tree insertion and deletion in Java. Compare the SML and Java implementations. Which features of which languages make the implementation easier and why?