CS307: Animation

Plan

• Recap and questions: Cross product
• Overview of basic animation
• Spinning cube and rotating stuff in Three.js
• Exercise: Moving & spinning cube — foiling the escape!
• Exercise: Moving parts — kick off!
• Recap and questions: Positional techniques for animation
• Example: Bouncing ball
• Exercise: Moving and decaying bouncing ball
• Brief note about detecting collisions
• Recap and questions: Absolute time
• Exercise: Jack-in-the-box

Recap: Cross Product

Basic Animation

We'll implement basic animation using the following approach:

• invoke the requestAnimationFrame() function, built into modern browsers
• (conceptually) loop through frames like this (it's like recursion):

  function next() {
      redoScene();
      TW.render();
      requestAnimationFrame(next);
  }

• stop animation with cancelAnimationFrame(), providing an id returned by requestAnimationFrame(), for example:

   
  // stored so that we can cancel the animation 
  var animationId = null;                
  
  function animate(timestamp) {
      oneStep();      // updates scene and renders
      animationId = requestAnimationFrame(animate);
  }
  
  function stopAnimation() {
      if ( animationId != null ) {
          cancelAnimationFrame(animationId);
      }
  }
  

• keyboard callbacks:

  TW.setKeyboardCallback("0", firstState, "reset");
  TW.setKeyboardCallback("1", oneStep, "take one step");
  TW.setKeyboardCallback("g", animate, "go: start");
  TW.setKeyboardCallback(" ", stopAnimation, "stop");
  




Of course, you don't need to have this interface — most of the Three.js and Dirksen animations just run immediately and forever.

Spinning Cube

Let's review the code for the spinning cube from the reading:

spinning cube with controls

Rotating Stuff in Three.js

There are two things to keep in mind when rotating things around multiple axes:

• the order of rotations around the X, Y, and Z axes matters
• Three.js has two ways to specify these rotations that are not equivalent

Let's explore these two points with the following demo:

three control cubes

• Initially, the leftmost cube (0) and "good" rotation method are selected. Rotate this cube by 90 degrees around the X axis and then 90 degrees around the Y axis (enter xxxxxxxxyyyyyyyyy)
• Select the middle cube (1) and perform the rotations in the opposite order (enter 1 and then yyyyyyyyyxxxxxxxxx). Observe the difference in behavior.
• Now select the rightmost cube (2) and "bad" rotation method (b) and repeat the 90 degree rotations around the X axis and then Y axis (enter 1, b, and xxxxxxxxxyyyyyyyyy) (so far so good...)
• With the rightmost cube and bad method still selected, continue with more rotation around the X axis (enter xxxx...) - is the cube correctly rotating around the "new" position of the X axis?
• Select the leftmost cube (0) and "good" method, and again continue with more rotation around the X axis (enter xxxx...) - how does the behavior compare to the "bad" method?

Here is the key piece of code that shows how the two rotation methods are implemented:

function setCubeRotation(time) {
    var degs = degrees(cubes[curr].rotation);
    console.log("before: " + JSON.stringify(degs));
    if ( rotationMethod == "bad" ) {
        switch(axis) {
        case "x": cubes[curr].rotation.x += TW.degrees2radians(10); break;
        case "y": cubes[curr].rotation.y += TW.degrees2radians(10); break;
        case "z": cubes[curr].rotation.z += TW.degrees2radians(10); break;
        default: throw "no such axis";
        }
    } else if ( rotationMethod == "good" ) {
        switch(axis) {
        case "x": cubes[curr].rotateX( TW.degrees2radians(10) ); break;
        case "y": cubes[curr].rotateY( TW.degrees2radians(10) ); break;
        case "z": cubes[curr].rotateZ( TW.degrees2radians(10) ); break;
        default: throw "no such axis";
        }
    }
    var degs = degrees(cubes[curr].rotation);
    console.log("after: " + JSON.stringify(degs));
}

These seem equivalent, but they are anything but!

Moving & Spinning Cube

In the following exercise, we'll add movement of the spinning cube in the X and Y directions, and stop the animation automatically when the cube leaves a surrounding wireframe "cage."

Moving Parts

Long ago, we constructed a jointed leg with nested frames. The code demo allowed us to move individual parts of the leg through the GUI controls. In the next exercise, we'll animate the leg, enabling each part to rotate through its full range of motion over the extent of the animation.

Positional Techniques for Animation

For positional techniques, updating the scene depends explicitly on the current time:

function updateState() {
    time += deltaT;
    updateModel(time);
    TW.render();
}

Bouncing Ball

Let's explore the bouncing ball demo from the reading:

bouncing ball

We know from physics that the height of a bouncing ball over time follows a cosine curve. The following plot shows |cos(t)| for values of t from 0 to 10:

Suppose we want the time period for each bounce to be some desired amount P. How can we use the cosine curve to determine the height of the ball at a particular moment in time?

Here, we want to map

• an input time that goes from 0 to P between bounces, to
• an output angle that goes from 0 to π between peaks of the cosine function.

We also want to know the height of the ball at a particular time, so we want to map

• an input value of the cosine function that ranges from 0 to 1, to
• an output height of the ball that ranges from the radius of the ball to a desired maximum height

The code for the bouncing ball defines a function, linearMap(), to help with this calculation. Given a value x for a quantity that ranges from minx to maxx, this function returns the corresponding value y on a scale that ranges from miny to maxy.

var y = linearMap(x, minx, maxx, miny, maxy);

Decaying Bouncing

In the real world, balls don't bounce forever, they come to a stop. Typically, the height of each bounce is a bit smaller than the one before, but it's not linear — instead, the height of each bounce is some fraction of the one before, looking something like this:

Brief Note About Detecting Collisions

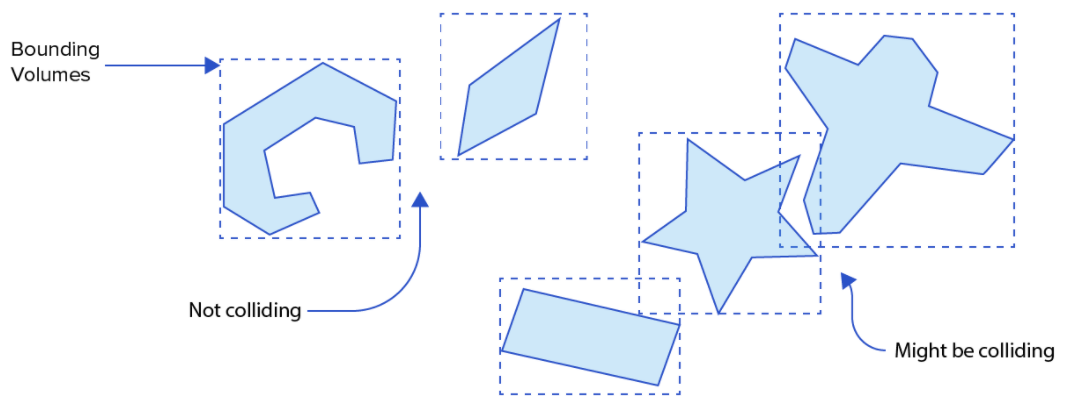
Imagine a set of objects moving in 3D — how can we detect potential collisions in a way that is computationally efficient? Bounding boxes enable a quick check for overlap in the volumes surrounding each object, but for complex shapes, this is a very challenging and computationally expensive task. Collision detection, and the related task of obstacle avoidance, are also important and challenging tasks in robotics.

Absolute Time

The time variable in the above examples is not absolute time. The JavaScript function setInterval() can be used to control the timing of an animation more closely, as shown with this spinning square:

spinning square

Here is the code, which uses the JS Date object to view the time of each call to drawSquare():

var square;
var nframes = 0;

function drawSquare () {
     console.log(new Date());      // note the changing seconds
     if (square != null) {
         scene.remove(square);
     }
     square = new THREE.Mesh(new THREE.PlaneGeometry(10,10),
                             new THREE.MeshBasicMaterial({color: 0x009900}) );
     square.rotation.z = nframes*(Math.PI/6);
     scene.add(square);
     nframes += 1;
     if (nframes > 10) {
         clearInterval(clock);     // stop the timer started with setInterval()
         console.log("stopped");
     } else {
         TW.render();
     }
}
var clock = setInterval(drawSquare, 1000);

Preparation for Next Time

Next time, we'll talk about advanced geometries, such as Bezier curves and surfaces, and lathe, extrude, and tube geometries. To prepare:

• Reading for Thursday: Bezier Curves and Surfaces
• Submit Sakai Quiz by Wednesday evening at 9:00 pm EST — you'll have an hour to complete the quiz, which is "open book/notes"

Due on Friday at 11:00 pm EST: HWK 4: Textured Barn and Creative Scene
(Note: automatic 48-hour extension on this assignment)