CS307: Bezier Curves

Plan

Review Bezier curves and blending functions
Bezier curves in Three.js
Quiz questions
Exercises: heart, ribbon, double ribbons
Thought exercises: Coke bottle & circle

Bezier Curves and Blending Functions

In computer graphics, we often need to model objects whose shape is defined by free-form curves:

bridge bezier cat luxo

A popular approach to modelling such shapes uses Bezier curves — let's first explore the basic ideas with this online tool.

We will represent a parametric curve $P(t)$ as a weighted sum of four control points, $P_0$, $P_1$, $P_2$, $P_3$:

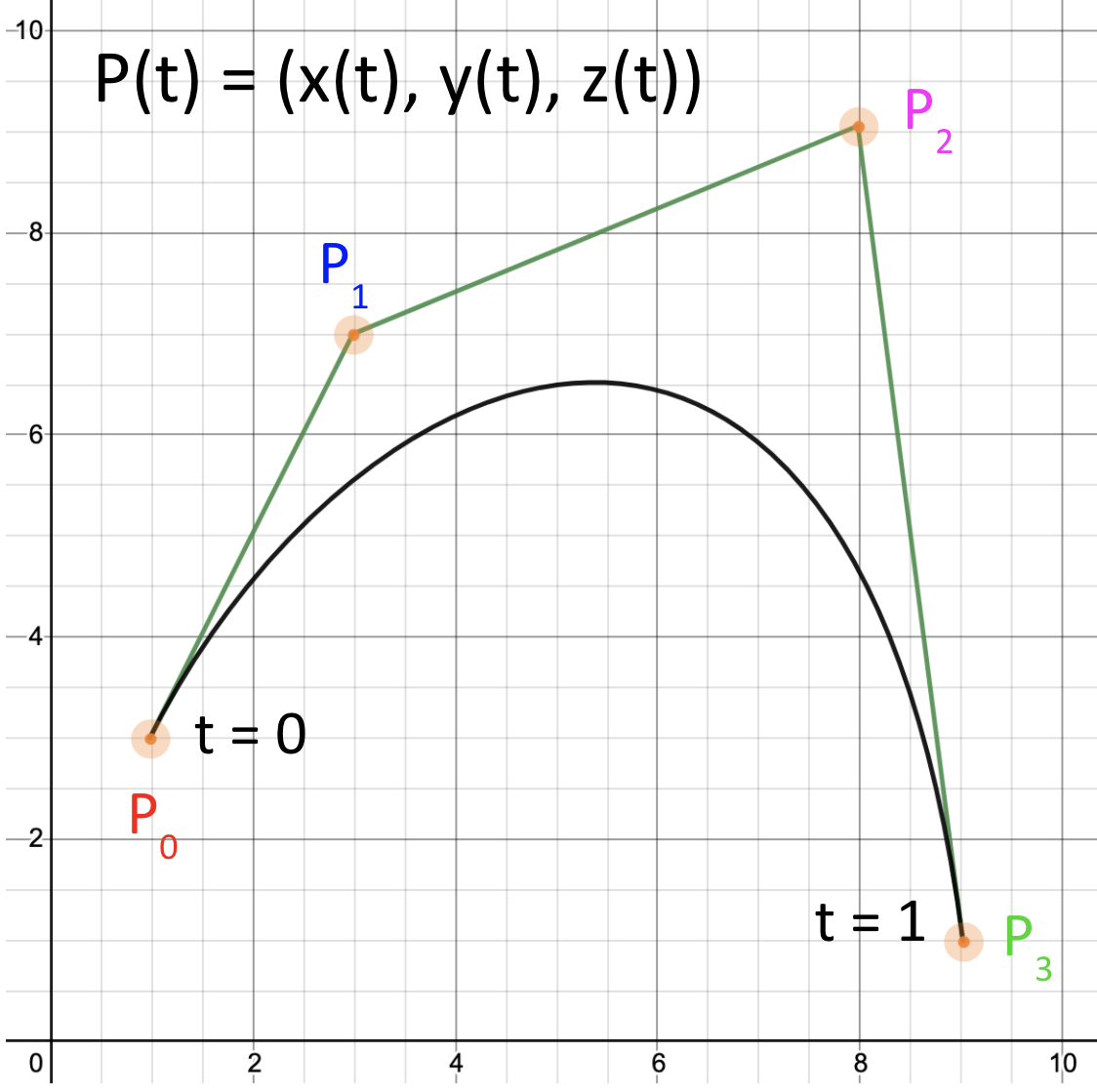
\begin{eqnarray*} P(t) &=& B_0(t)*P_0 + B_1(t)*P_1 + B_2(t)*P_2 + B_3(t)*P_3 \end{eqnarray*}

For each value of $t$, the weights are given by four blending functions, $B_0(t)$, $B_1(t)$, $B_2(t)$, $B_3(t)$:

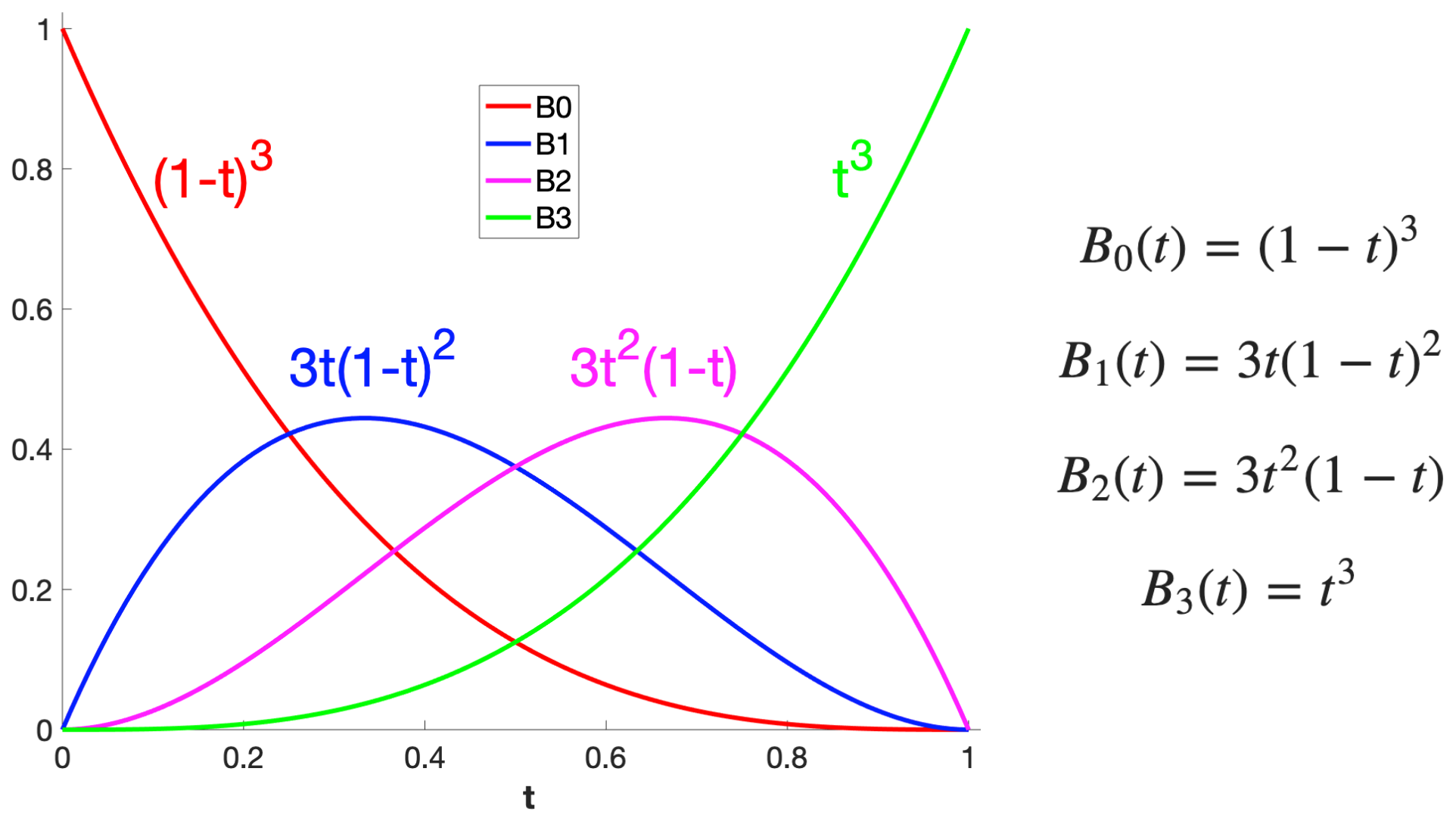
Some observations:

the first and last blending functions, $B_0(t)$ and $B_3(t)$, are monotonic
the blending functions are always non-negative
the four blending functions sum to one
the second and third functions peak at $t=1/3$ and $t=2/3$, respectively

The Bezier curve is always within the convex hull of the control points:

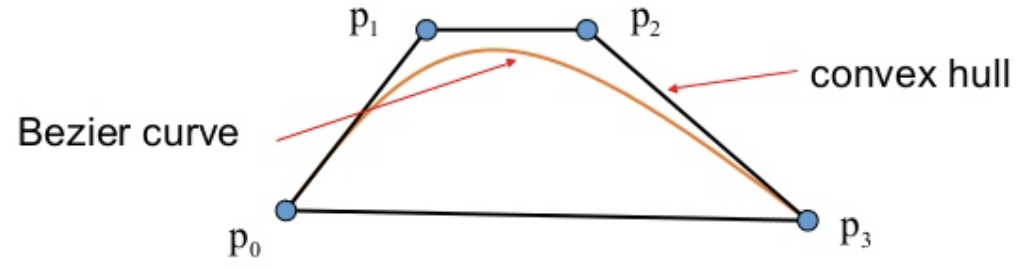
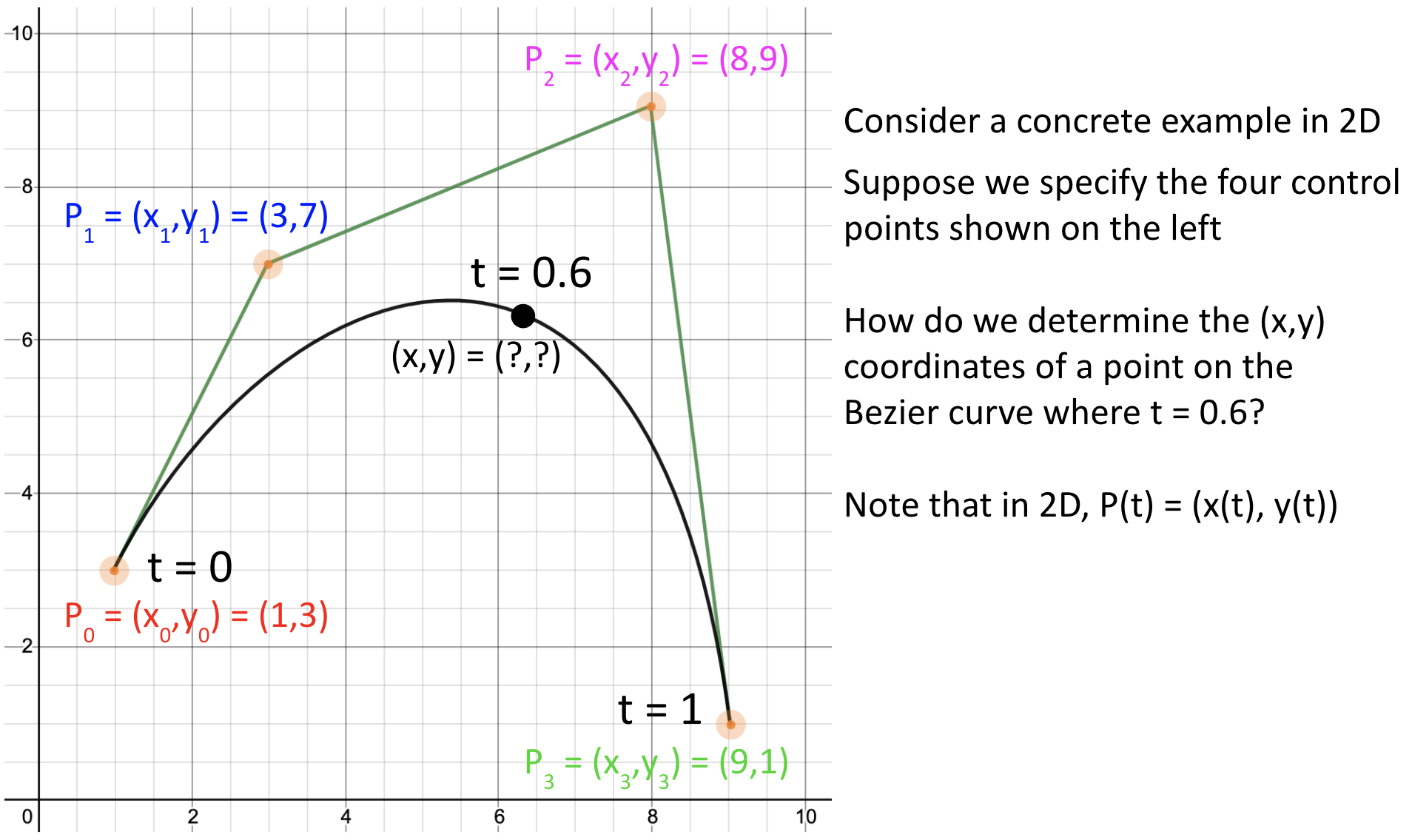
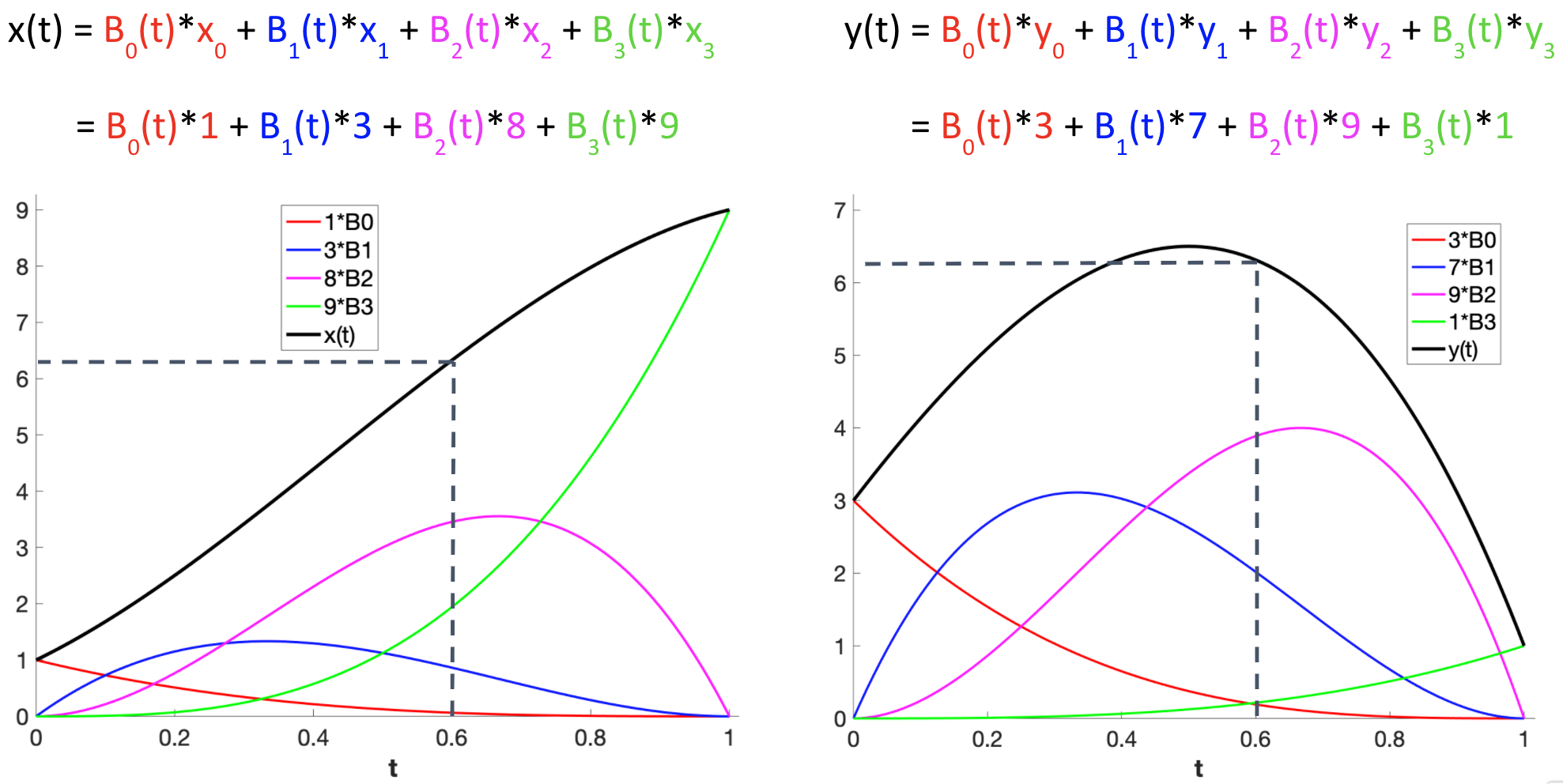
Bezier Curves in Three.js

We'll start with this demo of an S curve:

S curve

The code for this demo is quite short:

var controlPoints = [ [0,0,0],
                      [2,2,0],
                      [-2,1,0],
                      [0,3,0] ];
var curveGeom = TW.createBezierCurve(controlPoints,20);
var curveMat = new THREE.LineBasicMaterial( { color: 0xff,
                                              linewidth: 3 } );
var curve = new THREE.Line( curveGeom, curveMat );
scene.add(curve);

function showCP (cpList) {
    for( var i = 0; i < cpList.length; i++ ) {
        scene.add( TW.createPoint(cpList[i]) );
    }
};
showCP(controlPoints);          // optional, for debugging

This code depends on two functions in TW, which just make our lives a little easier. The first is TW.createBezierCurve():

The above function creates a THREE.CubicBezierCurve3.

The second function, TW.createPoint(), just displays a small sphere at the location of each control point, mainly to help with debugging.

To understand the role of the control points, let's play with the curve using a GUI:

S curve with a GUI

How many bends can you get in the curves? How tight a loop can you get?
Can you get this?

The following demo illustrates a 3D Bezier curve:

S curve in 3D

Quiz Questions

quiz questions

Exercises: Creating 2D Shapes from Bezier Curves

For each of the following exercises, use this S curve code file as a starting point to create the desired shape. You can use the S curve with a GUI or the online tool to help determine a good set of control points for each exercise.

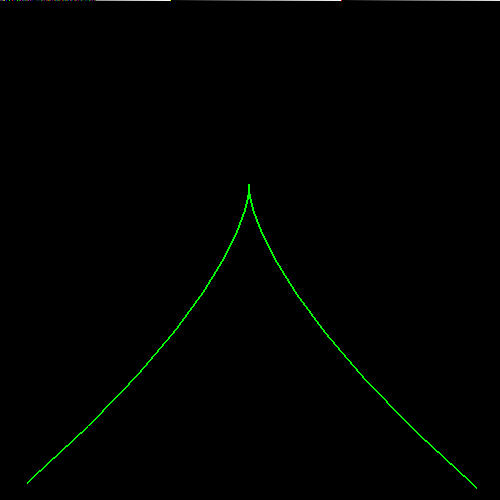
Heart

Using this S curve as a starting point, devise the control points to draw a heart, like this:

Hint: This requires two Bezier curves.

The result might look like this: heart curve

Here are two solutions with control points shown as spheres:
heart2.html heart3.html

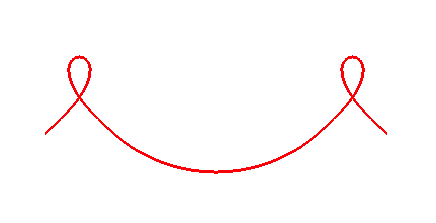
Ribbon

Using this S curve as a starting point, devise the control points to draw a ribbon, like this:

The result might look like this: ribbon curve

Double ribbons

Using this S curve as a starting point, devise the control points to draw a double ribbon, like this:

How many Bezier curves do you need in this case?

Hint for joining two Bezier curves smoothly:

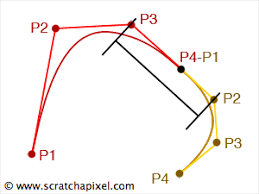
The result might look like this: double ribbon curve

Thought exercises

Here's a thought experiment: How would you draw the silhouette of a Coke^tm bottle?

Can you make a circle with a single Bezier curve? How or why not?