CS307: Bezier Curves & Surfaces, and Other Built-in Geometries
Plan
- Recap and questions: Bezier curves and blending functions
- Bezier curves in Three.js
- Exercises: heart, ribbon, double ribbons
- Bezier surfaces and the dome demo
- Exercise: Create your own Bezier surface
- Other built-in Three.js geometries: lathe, extrude, tube
- Katherine Kjeer's THREE.TubeRadialGeometry
- Exercise: Create your own tube geometry
Bezier Curves and Blending Functions
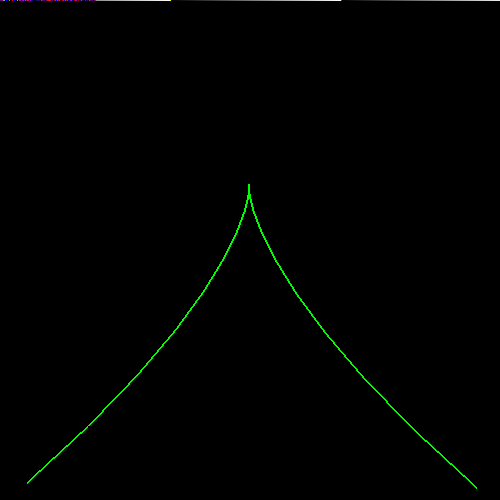
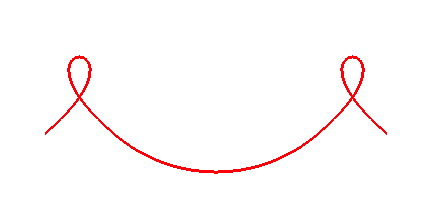
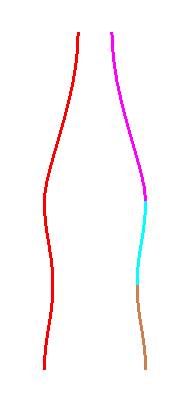
In computer graphics, we often need to model objects whose shape is defined by free-form curves:



A popular approach to modelling such shapes uses Bezier curves — let's first explore the basic ideas with this online tool.
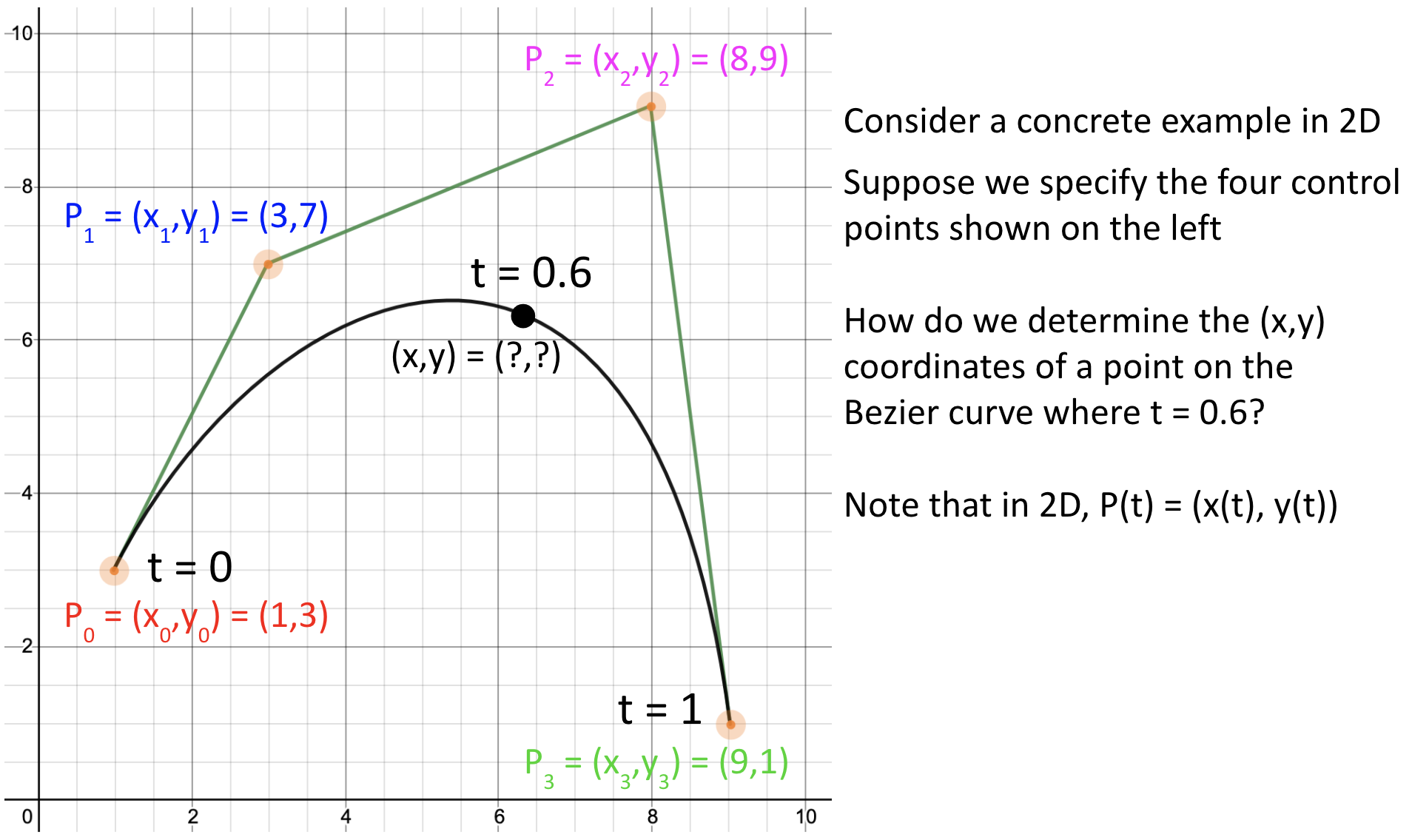
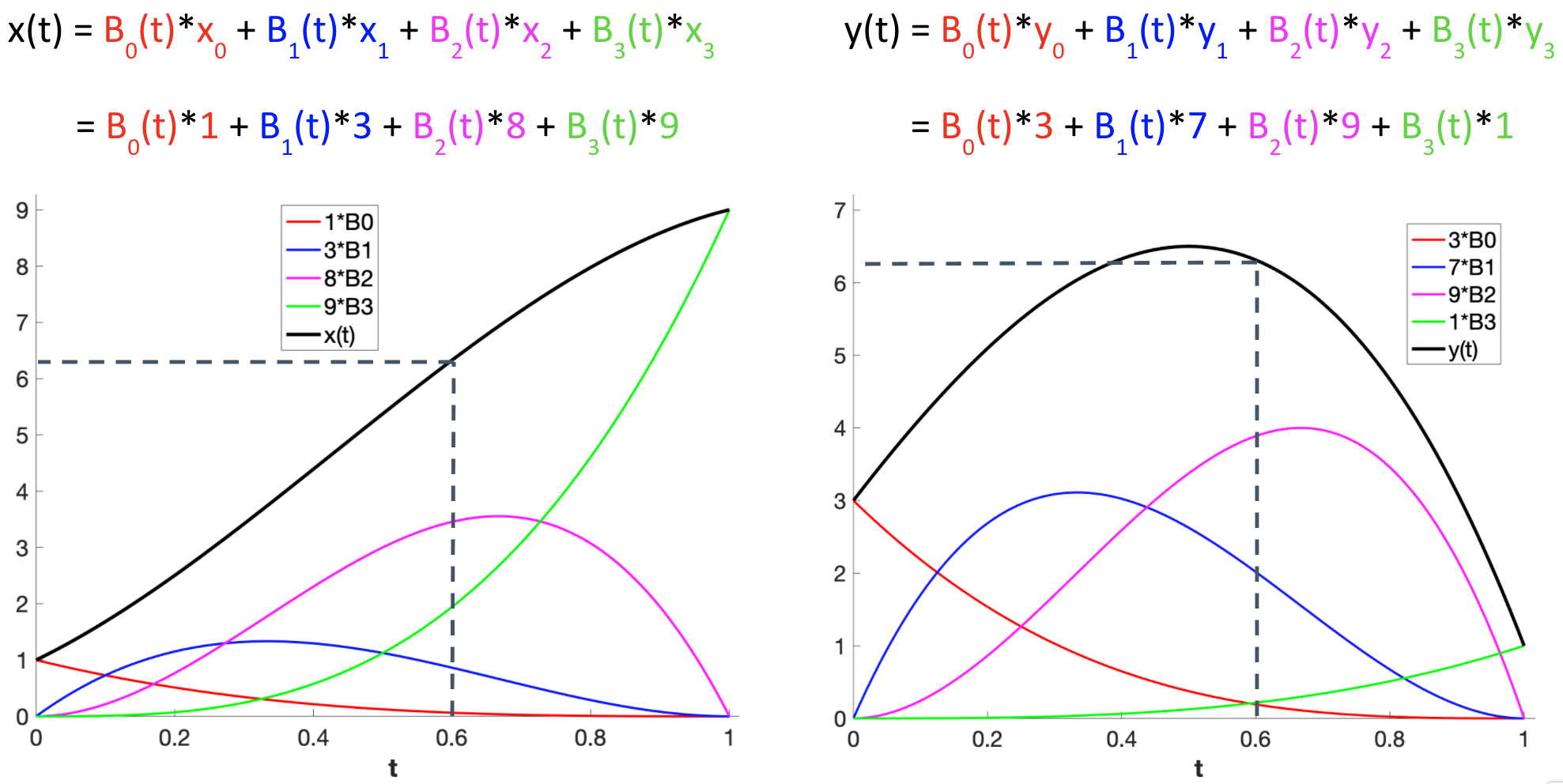
We will represent a parametric curve $P(t)$ as a weighted sum of four control points, $P_0$, $P_1$, $P_2$, $P_3$:
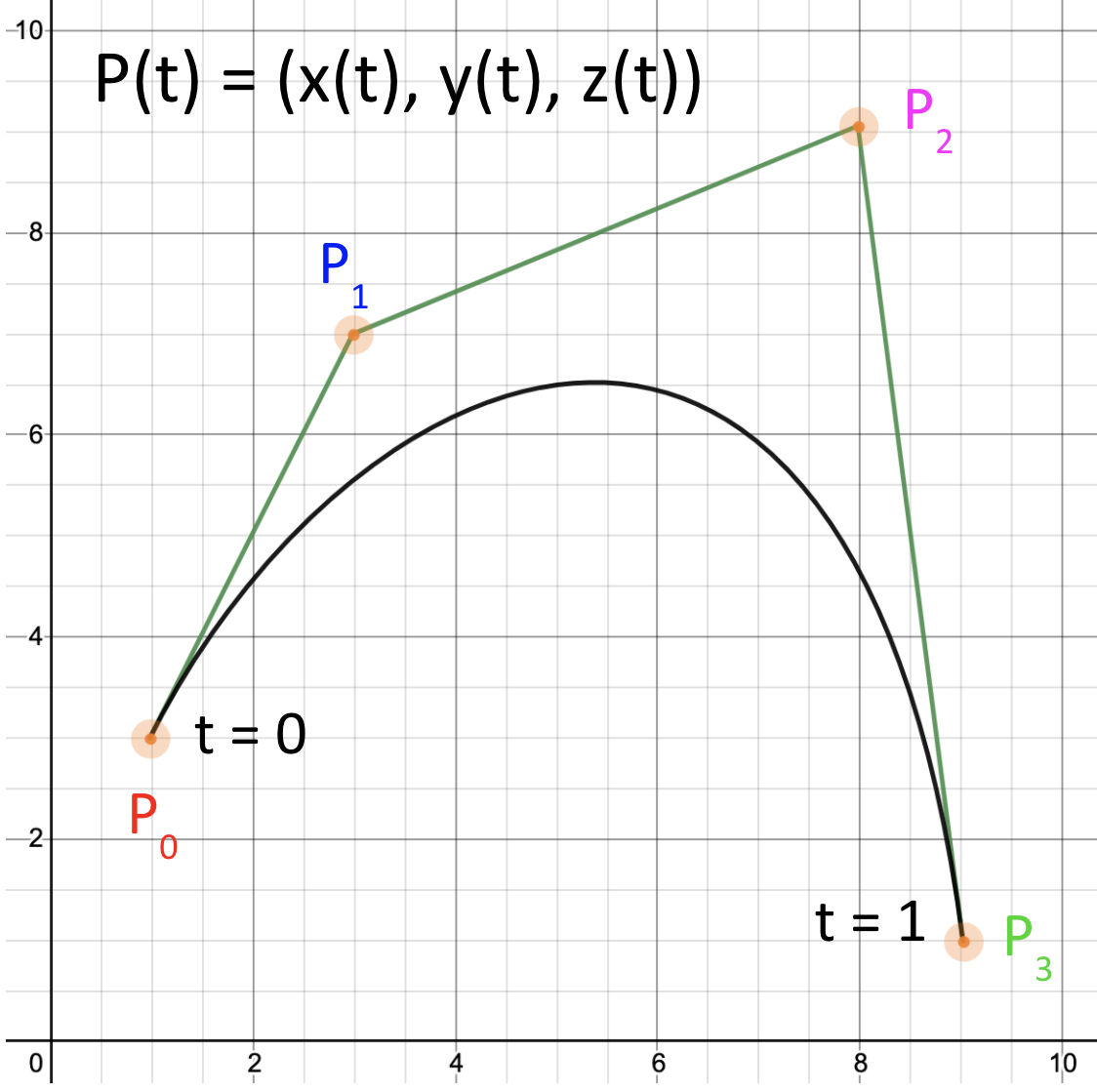
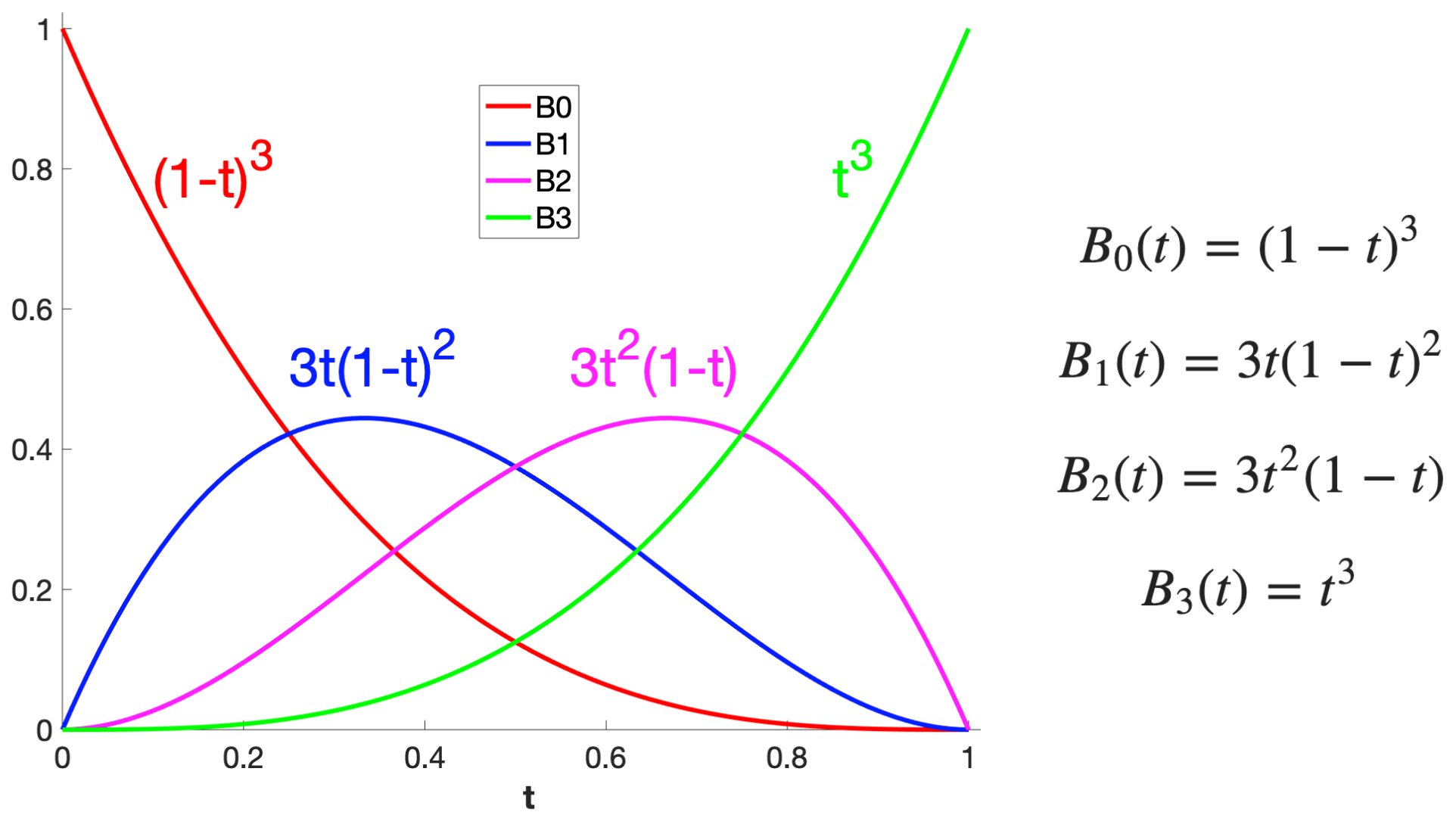
For each value of $t$, the weights are given by four blending functions, $B_0(t)$, $B_1(t)$, $B_2(t)$, $B_3(t)$:
Some observations:
- the first and last blending functions, $B_0(t)$ and $B_3(t)$, are monotonic
- the blending functions are always non-negative
- the four blending functions sum to one
- the second and third functions peak at $t=1/3$ and $t=2/3$, respectively
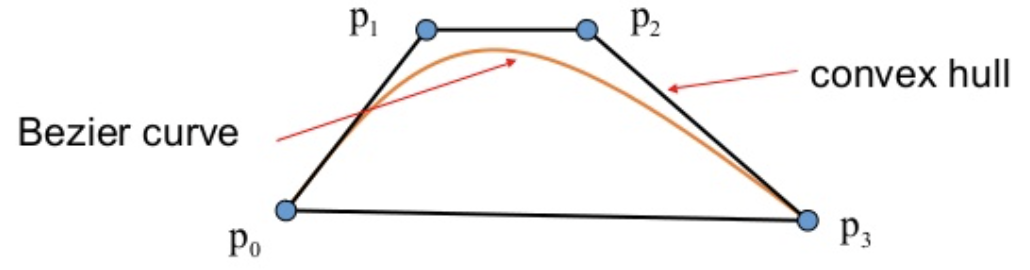
The Bezier curve is always within the convex hull of the control points:
Bezier Curves in Three.js
We'll start with this demo of an S curve:
The code for this demo is quite short:
var controlPoints = [ [0,0,0],
[2,2,0],
[-2,1,0],
[0,3,0] ];
var curveGeom = TW.createBezierCurve(controlPoints,20);
var curveMat = new THREE.LineBasicMaterial( { color: 0xff,
linewidth: 3 } );
var curve = new THREE.Line( curveGeom, curveMat );
scene.add(curve);
function showCP (cpList) {
for( var i = 0; i < cpList.length; i++ ) {
scene.add( TW.createPoint(cpList[i]) );
}
};
showCP(controlPoints); // optional, for debugging
This code depends on two functions in TW, which just make our lives a little easier. The first
is TW.createBezierCurve():
The above function creates a THREE.CubicBezierCurve3.
The second function, TW.createPoint(), just displays a small
sphere at the location of each control point, mainly to help with
debugging.
To understand the role of the control points, let's play with the curve using a GUI:
How many bends can you get in the curves? How tight a loop can you get?
Can you get this?
The following demo illustrates a 3D Bezier curve:
Exercises: Creating 2D Shapes from Bezier Curves
For each of the following exercises, use this S curve code file as a starting point to create the desired shape. You can use the S curve with a GUI or the online tool to help determine a good set of control points for each exercise.
Heart
Using this S curve as a starting point, devise the control points to draw a heart, like this:
Hint: This requires two Bezier curves.
The result might look like this: heart curve
Here are two solutions with control points shown as spheres:
heart2.html
heart3.html
Ribbon
Using this S curve as a starting point, devise the control points to draw a ribbon, like this:
The result might look like this: ribbon curve
Double ribbons
Using this S curve as a starting point, devise the control points to draw a double ribbon, like this:
How many Bezier curves do you need in this case?
Hint for joining two Bezier curves smoothly:
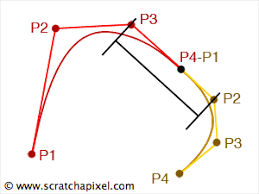
The result might look like this: double ribbon curve
Thought exercises
Here's a thought experiment: How would you draw the silhouette of a Coketm bottle?
Can you make a circle with a single Bezier curve? How or why not?
Bézier Surfaces
Bézier surfaces also use parametric equations to specify the surface, but we now have two parameters, s and t, and we have 16 control points (4x4).
\begin{eqnarray*} P(t) &=& (x(s,t), y(s,t), z(s,t)) \end{eqnarray*}
Let's first explore the creation of Bézier surfaces with this online demo on GitHub.
To create a Bézier surface in code, we first specify the 16 control points in the
following format, where each letter represents an array of coordinates, [x,y,z]:
var cps = [ [ A, B, C, D ],
[ E, F, G, H ],
[ I, J, K, L ],
[ M, N, O, P ] ]
var surfGeom = new THREE.BezierSurfaceGeometry(cps, 10, 10);
Because t increases upward, control point A is really the lower left, but visually that's difficult, so instead the code examples specify the control points from top to bottom. You'll see this in the dome demo.
var topToBottom = [ [ M, N, O, P ],
[ I, J, K, L ],
[ E, F, G, H ],
[ A, B, C, D ] ]
var surfGeom = new THREE.BezierSurfaceGeometry(topToBottom.reverse(), 10, 10);
For a Bézier surface:
- each edge is a Bézier curve
- the interior four points are hard to interpret, but intuitively, they pull the surface towards them
- all 16 points contribute to computing each point on the surface, except on the edges, when one parameter or the other is zero or one
- see Bézier blending functions for surfaces
- Bézier surfaces are used a lot in practice: bi-cubic patches, but decomposed into triangles
Dome
This demo omits texture-mapping, lighting, and complicated material.
Viewing the result and the code, where are the four control points that correspond to the four "corners" that the surface intersects (i.e. the endpoints of the Bézier curves around the edges of the surface)?
Exercise: Create your own Bézier surface
Using images like these as inspiration:




or anything else that's interesting to you, build a Bezier surface using the code for the dome as a starting point.
Tip: Use the topToBottom variable to set coordinates for your
control points. In the call to showCP() at the end of the file,
change the input from controlPoints to topToBottom.
Other Built-in Three.js Geometries
- lathe has the Y axis as the spine, a curve on the surface, and a spin around Y
- extrude has a shape in the XY plane and the Z axis is the axis of the extrusion
- tube has a circular cross-section and an arbitrary curve for the spine
Lathe Geometry
This is very useful. Let's explore an example that uses a THREE.LatheGeometry:
Lathe Geometries from Bezier Curves
The following example makes a Lathe geometry from our S curve that was created as a Bezier curve:
The following example creates a coke bottle using a silhouette that combines three Bezier curves:
Extrusion
Another interesting technique is to create a 2D shape and extrude it along a path defined by a 3D curve (by default, the Z axis). Dirksen has a nice example.
Also see the Three.js documentation: THREE.ExtrudeGeometry (not a great example)
Tubes
A nice technique is like extrusion along a curve, with circular cross-sections. See the Three.js documentation: THREE.TubeGeometry.
Katherine Kjeer's THREE.TubeRadialGeometry
Katherine Kjeer decided that tubes should allow variable radii, so she built it in Three.js.
Katherine's tubeDemo.html
Note that you can have as many radii as you want; Katherine just chose 4 as an example.
Exercise: Create your own tube geometry
Using this tube-start.html
code file as a starting point, and these images as inspiration, create an object using
Katherine's THREE.TubeRadialGeometry.



Here are some sample solutions: arch.html, horn.html, swissHorn.html