CS307: RGB Color

Plan

I'll address all of your quiz questions
Setting face colors in Three.js
Exercise: Penetrating triangles
Exercise: The flag of Seychelles
(optional) Exercise: Coloring the church
Coloring built-in geometries and the RGB color cube
Parametric equations and interpolation

RGB Color in Three.js and TW

Computer Graphics uses RGB color; Three.js has many ways to specify a color, but uses RGB internally

This simple color demo illustrates how to color each face of a geometry with a uniform color, using basic Three.js concepts. The slide in this handout shows the essential code for this example.

Key points about coloring faces in Three.js:

THREE.MeshBasicMaterial() can be used to give something a uniform RGB color
An array of materials can be used to give each face of a Mesh a different RGB color
A THREE.Face3 object has an instance variable named materialIndex that is an index into an array of materials, indicating which color to use for this face, so there is a connection between the geometry and the material
The TW module provides functions that make it easy to assign the same color to many faces of an object (TW.setMaterialForFaces()) or create a one-to-one mapping between an array of faces and an array of materials (TW.setMaterialForFaces11())
The TW.setMaterialForFaces11(geom) function is named because it sets up a 1:1 correspondence between faces and an array of materials.
The TW.setMaterialForFaces(geom, materialIndex, faceIndexes...) function Sets the material index for a list of faces, or all remaining arguments. Very often, you want to say faces [1, 2, 3, 7, 8] are all materialIndex M, and your code is five tedious assignment statements. This simplifies that. You can either give M and a list of face indexes, or all remaining arguments are the list of indexes.

Exercise: Penetrating Triangles

This exercise is inspired by the origami design with penetrating triangles shown below, from the Wonder How to Math Craft site (complete with assembly instructions):

The starting code file, triangles-start.html, contains a function named triGeometry() that creates a new THREE.Geometry with four penetrating triangles (move the camera around to view the four triangles). In this initial code, TW.createMesh() is used to create the Mesh for this Geometry.

Your task is to create an array of four materials (using THREE.MeshBasicMaterial) with four different colors, and use these materials to color the four triangles in the object. Use four different methods to specify the colors.

A couple tips:

The TW.setMaterialForFaces11() function may come in handy for setting the materialIndex so that the four faces are assigned, in order, to the four colors. This function has a single input geometry.
Set the side attribute for each material so that both sides of each face are rendered, as shown in the creation of a single color material below:
```
var myMaterial = new THREE.MeshBasicMaterial(
                       {color: new THREE.Color("blue"),
                         side: THREE.DoubleSide});
```

Here is a sample solution

Exercise: Flag of Seychelles

The goal of this exercise is to add colors to a graphical depiction of the national flag of Seychelles, shown below:

The starting code file, flag-start.html, includes a function flagGeometry() that creates a Geometry for the flag. The diagram below shows the ordering of the vertices.

The initial code creates a single white material for the flag. Your task is to color the triangular faces with the official colors of the Seychelles flag.

Note: There are two triangular faces for the red region of the flag. Specify the face colors in this exercise by setting the materialIndex property directly for each face, e.g.:

myGeom.faces[0].materialIndex = 1;

Here is a sample solution

Exercise: Coloring the Church

Starting with this church-start.html file, modify the code to create a white church with a brown roof and yellow steeple, as shown below:

The starting code provides comments about the steps to complete.

The barn has 16 faces (indices 0 to 15 in the array of faces), and the roof faces are stored at indices 6, 7, 8, and 9

Tip: You can specify one color for multiple faces all at once using the TW.setMaterialForFaces() function. The following example assigns a materialIndex of 2 (i.e. the material color at index 2 of the array of materials) to the faces 6, 8, and 9:

    TW.setMaterialForFaces(geom, 2, 6, 8, 9);

(Optional) Add a door and windows to the church using the built-in THREE.PlaneGeometry.

Sample solution code: church-color.html

Coloring a Built-in Three.js Geometry

We can also specify colors for built-in Three.js geometries, but depending on the number of segments we specify for the geometry, there can be a large number of faces and it can take some trial-and-error to figure out the order that the faces are added to the geometry.

Have a look at this colorful cone

The RGB Color Cube

In the above examples, each face had a single, uniform color (flat shading).

The RGB Color Cube uses vertex colors and interpolates colors over each face, creating the appearance of smoothly varying color over the surfaces of the cube (smooth shading). To understand the computation of interpolated color over a triangular face (next time!), we first explore interpolation in a simpler context of interpolating values over a line.

Parametric Equations and Interpolation

A few key points from the reading:

OpenGL uses parametric equations to represent lines
Given the coordinates of two points, A and B, the line containing these points can be expressed in terms of a single parameter t:
P(t) = A + vt
P(t) = A + (B-A)t
P(t) = A(1-t) + Bt

The vector v in the first expression runs from A to B, and is written explicitly as B-A in the second expression
Points along the line segment from A to B are generated with values of t from 0 to 1
The third expression above captures the idea that any point along the line segment from A to B has coordinates that can be thought of as a mixture of the coordinates of A and B

Below is an example of the parametric equation for a sample line containing two points, A and B. Values for the parameter t between 0 and 1 span the line segment between the two points. Note that the x,y,z coordinates can also be written as separate equations:

Exercise: Placing the Steeple on the Church

We did some guesswork arithmetic to find the correct place on the barn to position the steeple. The angle at the ridge is 90 degrees, which simplifies the arithmetic, but we may not always be so lucky.

Suppose we know that the vertex at the front of the ridge is R = (15, 55, 0) and the vertex at the shoulder of the barn is S = (0, 30, 0). Suppose we want to compute the vertex that is part of the base of the steeple, B, as a point one-fifth of the way down the roof from R to S.

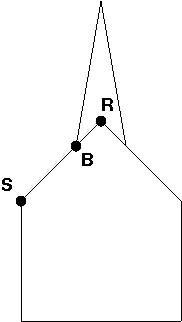
church vertices with R, B, and S

How can we compute the coordinates of B? (Don't assume that the ridge angle is 90 degrees.)

B = (4/5)R + (1/5)S
B = (4/5)*(15,55,0) + (1/5)*(0,30,0)
B = (12,44,0) + (0,6,0)
B = (12,50,0)

Colors, Interpolation and RGB

RGB color is a three-dimensional system just like our 3D spatial coordinates.

Color interpolation works pretty much the same way as spatial interpolation.

Exercise: Color Interpolation

Suppose the vertex S is cyan and R is magenta, what color is B?

color = (4/5)(magenta) + (1/5)(cyan)
color = (4/5)*(1,0,1) + (1/5)*(0,1,1)
color = (4/5,0,4/5) + (0,1/5,1/5)
color = (0.8,0.2,1.0)

To Do for the Next Class

Reading for Tuesday: HSL Color and Parametric Triangles