Reading: User Interaction

Skip ahead to Mouse Movement

So far, we've mostly been creating images and animations, rather than interacting with the user. Our interaction has mostly been limited to keyboard callbacks using TW or GUI controls, and even that has been mostly toggling global settings such as lighting or textures, or adjusting parameters. This is fine for producing animations (after all, Pixar movies aren't interactive), but if we want to do games and other kinds of interactive software, we'll need to do better. In this reading, we'll start digging into how to have a more interactive program.

Note that user interaction isn't really part of OpenGL per se. OpenGL is about graphics, not about handling mouse clicks or keyboard input, or tangible user interfaces or any of the many other ways that we can imagine interacting with our devices.

Nevertheless, if you want to build a game or any other software that combines computer graphics with user interaction (even an animation might have a pause/resume feature), we'll want to confront this.

Interaction in a Web Browser

Web browsers have a reasonably straightforward way of handling keyboard input — until you start looking into it more deeply. Then it becomes a mess. But, let's ignore the mess for now and start with some straightforward elements.

When the keyboard changes state (a key goes up or down ...) the browser generates an event, which you can add a handler for. The easiest one to work with is keyPress. (The keypress event is deprecated, but may still be supported by most browsers for the foreseeable future.) Here's how you bind it:

document.addEventListener('keypress', onKeyPress);

function onKeyPress (event) {
   var key = event.keyCode;
   ...
}

As you can see, you bind the keypress event to a callback function that is invoked whenever a key is pressed. This callback function is invoked with an object that represents all the information about the event. The property we will care about is the keyCode (which is also deprecated, but as of Fall 2018 Google Chrome 69.x provides key, which is the intended replacement. Again, we'll proceed as if all is well, which it probably will be).

The keyCode property returns a numerical code for the key, which is just the Unicode codepoint for the character (we'll mostly stick to ASCII), but if you want to handle a broader range of characters, be my guest.

Working with numerical codes is awkward at best, and a recipe for unreadable code at worse. Computer geeks like myself may have memorized the fact that an upper case 'A' has the numerical code 65, but your code should not have ASCII or Unicode constants like that in it. To convert a Unicode codepoint to a character, you can do this:

function onKeyPress (event) {
   var key = event.keyCode;
   var ch = String.fromCharCode(key);
   alert("You typed a " + ch);
   ...
}

The key attribute of the event object is already a character, so if you use key, you can skip this conversion.

What you'll next want to do is figure out what key was pressed and then do something appropriate. For now, let's imagine that what you want to do is something to create a WASD interface to move an avatar around the scene while using a mouse with your right hand:

function onKeyPress (event) {
   var key = event.keyCode;
   var ch = String.fromCharCode(key);
   switch (ch) {
       case 'w': goForward(); break;
       case 's': goBackward(); break;
       case 'a': goLeft(); break;
       case 'd': goRight(); break;
       default:
           console.log("key " + ch + " is not handled");
   }
}

There are, of course, many variations on this kind of code. For example, several similar blocks might be coalesced. You might invoke TW.render() after every keypress, in case it changed the scene, and relieving every keybinding from having to do that.

The most important disadvantage of using keypress is that it only handles keys that send a Unicode character to the computer. Other keys, most importantly, the arrow keys and other special keys like PageUp and Home, do not generate keypress events. If you want to process those, you can use the keydown event, but that provides you with numerical key identifiers, and those are a pain to process. (For example, both an uppercase and lowercase 'a' are the same key, so they send the same code. You have to look at the modifier information. Also, some of the keys send same numbers as certain ASCII codes. Again, see pages like JavaScript madness for details.) In this course, we're not going to worry too much about portability. If it works on your computer and mine, that's good enough.

For simplicity, we'll stick to keypress.

The event object can also tell whether the shift, control, alt, or meta keys are down, so you can treat Control-A differently from a or A.

Mouse Coordinates

When the monitor redraws the screen, it starts in the upper left corner and the electron gun sweeps left to right and top to bottom. For that reason, browsers use a coordinate system where the origin is at the upper left, the $x$ coordinate increases to the right and the $y$ coordinate increases going down. The mouse coordinates are reported in window coordinates, which is in pixels measured from the upper left. If your browser is in a 960 by 500 window, those values will be, respectively, the largest possible $x$ and $y$ coordinates. See this figure:

Suppose you want to process mouse clicks, then the event you want to bind is, unsurprisingly, click. Thus, the code might look like this:

document.addEventListener('click', onMouseClick);

function onMouseClick (event) {
    var mx = event.clientX;
    var my = event.clientY;
    console.log("click at (" + mx + "," + my ")");
}    

Don't you wish it were that easy? Unfortunately, when we are using a canvas in a web browser, the absolute mouse coordinates aren't exactly what we want. Instead, we'd like to have the coordinates specified relative to where our canvas is (and there might be more than one). See this figure:

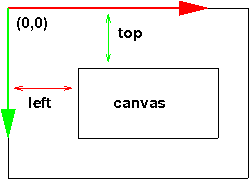
To adjust for the location of the canvas within the window, we need to find out the target of the click (what element was clicked on), and then we can find out its offset from the window, using the very useful getBoundingClientRect() function. Suppose that we previously saved the canvas in a variable c1. Our code then becomes:

function onMouseClick (event) {
    var mx = event.clientX;
    var my = event.clientY;
    console.log("click at (" + mx + "," + my + ")");
    var target = event.target;
    if( target == c1 ) {
        console.log("clicked on a canvas");
        var rect = target.getBoundingClientRect();
        var cx = mx - rect.left;
        var cy = my - rect.top;
        console.log("clicked on c1 at (" + cx + "," + cy + ")");
    }
}    

If you care about which button was clicked (left, middle, right), the event object has a button property that gives the numerical index of the button. Zero is the left button, one is the middle button, and so forth. It may be hard to capture a right-click, since the browser usually intercepts that and processes it specially.

Mouse Movement

After processing mouse clicks, you may want to process mouse movement, say to implement click and drag. For this, we need a few more events:

document.addEventListener('mousemove', onMouseMove);
document.addEventListener('mousedown', onMouseDown);
document.addEventListener('mouseup', onMouseUp);

As before, the event handler is called with an event object that has the information about the event.

To implement dragging, you will need to notice when the mouse button goes down and up, and when it moves while the mouse is down. Something like this:

var isMouseDown = false;

function onMouseDown (event) {
    isMouseDown = true;
}
    
function onMouseUp (event) {
    isMouseDown = false;
}

function onMouseMove (event) {
    if( isMouseDown ) {
        console.log("drag to (" + event.clientX + "," + event.clientY + ")";
    }
}    

Notice that these functions only give you a snapshot of the mouse motion. It doesn't tell you where the mouse was, how it was moving, or anything like that. In our geometry terminology, it gives you a point, not a vector. Yet you often want to know what direction the mouse was moving. For example, in the GUI for moving the camera viewpoint, if you drag the mouse down, you get a very different effect than if you drag it to the right, even if you end up at the same location. The callback will only get the location, not the direction, so how to do this? The answer is simply to keep track of where the mouse was:

var oldMouse = {x:0, y:0};

function onMouseMove (event) {
    if (isMouseDown) {
        console.log("drag to (" + event.clientX + "," + event.clientY + ")"
                    + "from (" + oldMouse.x + "," + oldMouse.y + ")");
        oldMouse.x = event.clientX;
        oldMouse.y = event.clientY;
    }
}

Here is a demo that puts all of these ideas together. Please take a few minutes to read the source code; it's less than 100 lines of code.

events.html

Unit Camera Movement

Suppose that we are using the mouse and keyboard callbacks (we'll combine the two soon). When the mouse is in the left half of the window, a key press or mouse click means move to the left, and similarly if the mouse is in the right half of the window. (In the gaming community, this sort of movement is known as strafing.) Also, if the mouse is in the upper half of the window, a key press or mouse click means move up, and similarly an action in the lower half means move down. Assuming (for the sake of simplicity), that the camera is facing down the $-Z$ axis, how can we implement this sort of movement?

First, we need to know how big the window is, so that we can know where the middle is. Let's set up global variables to record this. These could be constants, but if we want to allow the user to reshape the window, we would set up a reshape event handler (another DOM event; we'll leave that aside for now) that would modify these values if the window changes size.

var winWidth = 400;
var winHeight = 200;

Assume that the camera is set up using at and eye points, as we did back when we learned that API.

var eye = THREE.Vector3(...);
var at  = THREE.Vector3(...);

Our callback function can then operate as shown below. Note how this enforces our assumption that the camera is always facing parallel to $-Z$.

function onMouseClick (event) {
    ... // compute (cx,cy)
    var x = cx - winWidth/2
    var y = winHeight/2 - cy;
    moveX( x > 0 ? +1 : - 1);
    moveY( y > 0 ? +1 : - 1);
    TW.render();
}

function moveX (amount) {
     eye.translateX(amount);
     at.translateX(amount);
}
    
function moveZ (amount) {
     eye.translateZ(amount);
     at.translateZ(amount);
}

Let's focus on the first two lines of the callback function. Essentially what we're doing is mapping to a coordinate system where (0,0) is in the center of the window, $x$ increases to the right and $y$ increases up (whew!). This easily divides the window into the four signed quadrants that we're used to. See this figure:

The rest of the callback is straightforward.

Proportional Camera Movement

In the previous section, we're throwing away a lot of information when we just use the sign of the mouse coordinates. Why not move the camera a lot if the mouse click is far from the center, but only a little if it is close to the center? That is, we could make the amount of movement proportional to the distance from the center. Now our mouse is becoming useful. Building on the ideas from the previous section, our coding is fairly straightforward.

Recall that the maximum absolute value of the mouse coordinates is half the window width or height. If someone clicks at the extreme edge and we want that to result in, say, the camera moving by maxX or maxY units, we can arrange for that with a straightforward mathematical mapping. We first map the $x$ and $y$ coordinates onto the range [-1,1] by dividing by their maximum value. Then, multiply that by the largest amount we would want to move. (Call that the xSpeed and ySpeed.)

The JavaScript code is as follows:

var xSpeed = 3.0;   // just an example
var ySpeed = 4.0;   // just an example

function onMouseClick (event) {
    ... // compute (cx,cy)
    var x = cx - winWidth/2
    var y = winHeight/2 - cy;

    moveX(xSpeed * x/(winWidth/2));
    moveY(ySpeed * y/(winHeight/2));

Oh, that's so much better! We even avoid the ternary operator.

Thus, if the user clicks in the middle of the lower right quadrant (the $+-$ quadrant), $x$ will have a value of $+0.5$ and $y$ will have a value of $-0.5$, and so moveX will be invoked with 1.5 and moveY with -2.0.

Of course, we're not limited to a linear proportionality function. If, for example, we used a quadratic function of the distance, mouse clicks near the center could result in slow, fine movements, while clicks far from the center could result in quick, big movements. This could be useful in some applications.

Picking and Projection

So far, our interaction has been only to move the camera, but suppose we want to interact with the objects in the scene. For example, we want to click on a vertex and operate on it (move, delete, inspect, or copy it, or whatever). The notion of clicking on a vertex is the crucial part, and is technically known as picking, because we must pick one vertex out of the many vertices in our scene. Once a vertex is picked, we can then operate on it. We can also imagine picking line segments, polygons, whole objects or whatever. For now, let's imagine we want to pick a vertex.

Picking is hard because the mouse location is given in window coordinates, which are in a 2D coordinate system, no matter how we translate and scale the coordinate system. The objects we want to pick are in our scene, in world coordinates. What connects these two coordinate systems? Projection. The 3D scene is projected to 2D window coordinates when it is rendered.

Actually, the projection is first to normalized device coordinates or NDC. NDC has the x, y, and z coordinates range over [-1,1].

You might wonder about the existence of the z coordinate. Since we've projected from 3D to 2D, aren't all the z values the same? Actually, the projection process retains the information about how far the point is by retaining the z coordinate. The view plane (the near plane) corresponds to an NDC z coordinate of -1, and the far plane to an NDC z coordinate of +1.

The NDC coordinates are important because OpenGL will allow us to unproject a location. To unproject is the reverse of the projection operation. Since projecting takes a point in 3D and determines the 2D point (on the image plane) it projects to, the unproject operation goes from 2D to 3D, finding a point in the view volume that projects to that 2D point.

Obviously, unprojecting an (x,y) location (say, the location of a mouse click) is an under-determined problem, since every point along a whole line from the near plane to the far plane projects to that point. However, we can unproject an (x,y,z) location on the image plane to a point in the view volume. That z value is one we can specify in our code, rather than derive it from the mouse click location.

Suppose we take our mouse click, (mx,my), and unproject two points, one using z=0, corresponding to the near plane, and one using z=1, corresponding to the far plane. (At some point, the API changed from NDC to something similar but with z in [0,1].)

var projector = new THREE.Projector();
var camera = new THREE.PerspectiveCamera(...);

function pick (mx,my) {
    var clickPositionNear = new THREE.Vector3( mx, my, 0 );
    var clickPositionFar  = new THREE.Vector3( mx, my, 1 );
    projector.unprojectVector(clickPositionNear, camera);
    projector.unprojectVector(clickPositionFar, camera);
    ...
}

What this does is take the mouse click location, (mx,my), and find one point on the near plane and another on the far plane. The Three.js Projector object's unprojectVector() method modifies the first argument to unproject it using the given camera.

Thought question: If we drew a line between those two unprojected points, what would we see? Here's a demo that does exactly that:

click

Ray Intersection

Our next step in picking is to take the line between those two points, and intersect that line with all the objects in the scene. The Three.js library has a Raycaster object that has a method that will take a point and a vector and intersect it with a set of objects. It returns a list of all the objects that the ray intersects, sorted in order of distance from the given point, so the first element of the returned list is, presumably, the object we want to pick.

The (old) Three.js library comes with an example that demonstrates this very nicely:

WebGL Interactive Cubes

You're encouraged to look at the code for that example.

The example that allows you to click to create points and click-and-drag to move them employs all of these techniques:

draw moveable points with shift+click

Event Bubbling

In this reading, we've always bound the listeners to the document, but if your graphics application is running in a canvas on a larger page that has other things going on, you might bind the listener to some parent of the canvas instead. An issue that can arise is that the other applications may also bind the document and then both event handlers might get invoked. This is called event bubbling. If you want to learn more, you might start with the Quirk Mode page on Event Bubbling. There are, of course, other explanations on the web as well.