Color, part b

Please click through to the color cones demo.

Be sure to look at it from the side (+X direction) by using the "x" key or dragging with the mouse.

The demo has some additional keyboard callbacks:

• The + and - keys adjust the number of wedges in the color pyramids.
• The 1 and 2 keys display either both color pyramids or just the first one (with black at the apex).

The code for the Color Cone Scene is here. Note how the keyboard callbacks are set up.

Finally, if you're curious, here is how the color pyramids are built:

Understanding polar coordinates like this is important, so take a few minutes to understand this code, particularly lines 27--35. This figure may help:

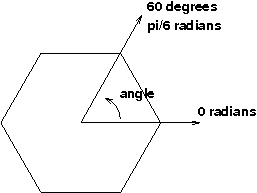
The main computations that, for angles counter-clockwise around the origin:

x = radius * cosine( angle )
y = radius * sine( angle )

Keyboard Callbacks

The Color Cone demo allowed you to adjust the number of vertices up and down. That code can be broken down into three simple parts:

• A set of global values used by the Three.js code to create the scene.
• An anonymous function that modifies those global values, reconstructing anything the model from them, and then re-draws (renders) the scene. This is the callback.
• Code to register the callback function and associate it with a key. Use TW.setKeyboardCallback() after TW.cameraSetup(), which is when the built-in key callbacks are set up.

This technique will let you dynamically adjust many aspect of your models very easily.

In the color cone demo above, we saw triangles that smoothly changed from one color to another across then. Next, we'll look at how that's done. This builds on what we learned last time about parametric equations of lines, so you should refresh your memory if necessary. A parametric equation for a line from A to B is:

P(t) = A + (B-A) t

Parametric Equation for a Triangle

Since a triangle is a 2D thing, the parametric equation for a triangle will have two parameters. One way to think about these two parameters is that the first parameter, say t, moves you along one side of the triangle, from vertex A to vertex B. Let P(t) be that point along the AB edge of the triangle. The second parameter, say s, is the parameter of a line from vertex C to P(t). That is, the endpoint of the second line is a moving target. The point Q(s,t) is a point in the triangle, on a line between C and P(t).

The following figure sketches these ideas:

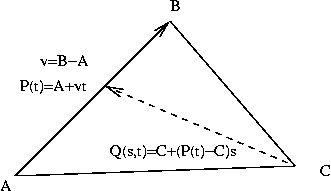
Q(s,t) = C + (P(t) -C)s
Q(s,t) = C + (P(t)s - Cs)
Q(s,t) = [A(1-t)+B(t)]s + C(1-s)
Q(s,t) = A(1-t)s+Bts + C(1-s)

Notice that we have several choices: the line from A to B could instead go from B to A. Similarly, the line from C to P(t) could go from P(t) to C. These yield equivalent equations, just as the equations of a line from A to B is equivalent to a the equation of a line from B to A.

The last line of the math for Q(s,t) above shows a three-way mixture of the vertices. That is, a triangle is all points in the convex sum of the vertices. A convex sum is a weighted sum of N things, where the weights all add up to 1.0:

w1*A+w2*B+w3*C
w1+w2+w3 = 1

Compare this to the weighted sum formula for Q(s,t). The last equation is perhaps a little surprising, but you can check that the weights sum to one:

(1-t)s+ts+(1-s)=1

Incidentally, the center of the triangle is when all the weights are equal: one-third.

Example: Finding the Equation of a Triangle from Three Points

Suppose we have a triangle ABC whose vertices are:

A = (1,2,3)
B = (2,4,1)
C = (3,1,5)

We could write down the following equation for the triangle:

Q(s,t) = A(1-t)s + B(t)s + C(1-s)
Q(s,t) = (1,2,3)(1-t)s + (2,4,1)ts + (3,1,5)(1-s)

So, doing each coordinate separately, we have:

x(s,t) = (1-t)s + 2ts + 3(1-s)
y(s,t) = 2(1-t)s + 4ts + (1-s)
z(s,t) = 3(1-t)s + ts + 5(1-s)

Which we can simplify algebraically to

x(s,t)	= (1-t)s + 2ts + 3(1-s)
	= s-ts+2ts+3-3s
	= ts-2s+3

y(s,t)	= 2(1-t)s + 4ts + (1-s)
	= 2s -2ts + 4ts + 1-s
	= 2ts + s + 1

z(s,t)	= 3(1-t)s + ts + 5(1-s)
	= 3s -3ts + ts + 5 - 5s
	= -2ts -2s + 5

Suppose we have a point whose parameters with respect to that triangle are (0.5,0.5). What does that mean? It means that the point is halfway between C and the midpoint of AB. The coordinates are:

x(0.5,0.5) = (0.5)(0.5)-2(0.5)+3 = 2.25
y(0.5,0.5) = 2(1-0.5)0.5 + 4(0.5)(0.5) + (1-0.5) = 2
z(0.5,0.5) = 3(1-0.5)0.5 + (0.5)(0.5) + 5(1-0.5) = 3.25

Equivalently, we can think of computing Q(s,t) as a weighted sum of the triangles vertices:

Q(s,t) = A(1-t)s + B(t)s + C(1-s)
Q(0.5,0.5) = A(1-0.5)(0.5) + B(0.5)(0.5) + C(1-0.5)
Q(0.5,0.5) = A(0.25) + B(0.25) + C(0.5)

Then, to find the coordinates of Q(0.5,0.5), we just substitute the coordinates of ABC and calculate the weighted sum.

Color Interpolation in a Triangle

If the colors of the vertices are different, OpenGL interpolates them, using the same equations that we used for calculating coordinates. Suppose A is red (1,0,0), B is magenta (1,0,1) and C is yellow (1,1,0). We can compute the color of the middle point, Q(0.5,0.5), as:

Q(0.5,0.5) = A(0.25) + B(0.25) + C(0.5)
Q(0.5,0.5) = (1,0,0)(0.25) + (1,0,1)(0.25) + (1,1,0)(0.5)
Q(0.5,0.5) = (1,0.5,0.75)

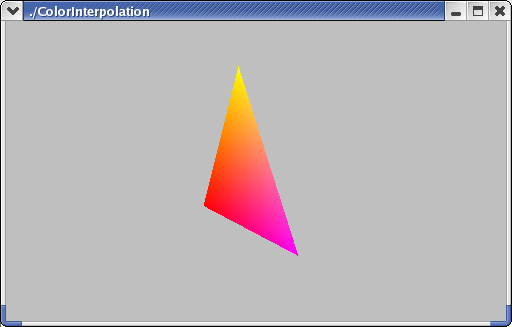
The triangle as a whole looks like this.

Bilinear Interpolation for a Quadrilateral

A quad works the same way, except that now the parameter t moves along both sides of the quadrilateral. In the figure below, t might move us from A to B and simultaneously from C to D. Meanwhile, s moves us from P(t) along the upper edge down to Q(t) along the lower edge.

Thus,

R(s,t) = (1-s)P(t) + sQ(t)

Color Interpolation in OpenGL

In a hardware implementation, the graphics card figures out the intersection of the projection of two segments with a scan line (one of the lines of the raster, corresponding to a horizontal line of pixels on the monitor). That gives the colors of both endpoints. Then, it fills the pixels in between, stepping the color by the same amount at each step. If there are 100 pixels between the edges of the projection, the color is stepped in 99 equal-size increments.

Don't rely on OpenGL to do bi-linear interpolation on quads or the right thing for general polygons. It's much better to break it down into triangles and use that. This is because graphics cards break larger polygons into triangles for fast processing. THREE.js does this for us.

Suppose you have a quad with three red vertices and one white vertex. You might expect a smooth gradient of pinkness as you approach the white vertex. In fact, it depends entirely on which vertex is the white one. If it's the fourth vertex, the triangulation will leave that vertex entirely out of the first triangle, and so the first triangle will be solid red. The second triangle will have the shading you expect, though starting closer than you'd expect. However, if the white vertex is the first vertex, both triangles will have a white vertex, and so you'll get much more of the shading you'd expect, though, in fact, neither will match the result you'd get with bi-linear interpolation.

The following figure demonstrates several different results of drawing a quad with smooth shading and each vertex having a different color. In every case, vertices are given to OpenGL in clockwise order; in this case, starting at the lower left (the red vertex). It goes Red, Green, Blue, Yellow.

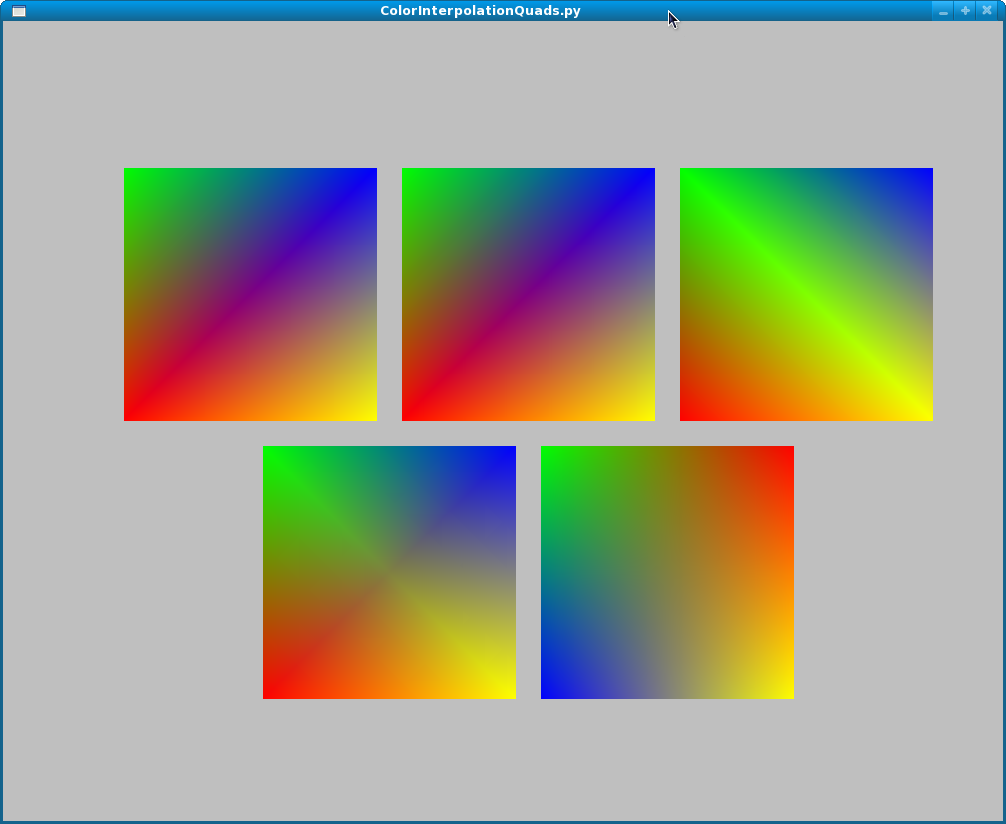
The pictures in the first row are (1) a quad with RGBY vertices with the first vertex being the lower left one and proceding clockwise, (2) two triangles cut along the diagonal from lower-left to upper-right, (3) two triangles cut along the diagonal from upper-left to lower-right. Note that the quad matches the second figure, not the third. This shows that the triangulation is done as you'd expect: the first three vertices are formed into a triangle, then the next three.

The pictures in the second row are (4) the quad cut into four triangles using the middle point, and (5) the quad cut into 400 quads using a mesh.

The main problem is that the two triangulations are different, when you might think it wouldn't matter. (With flat shading, they don't, because the fourth vertex determines the color.) Next, none of the elements on the first row matches the four-part triangulation in the second row. The fifth version is the smoothest yet, but you might think they should all match.

Color Interpolation in Three.js

The following FAQ is a little out of date, but it does explain how to do color interpolation in Three.js.

The key elements are:

1. The THREE.Geometry() object will have a vertexColors property that is an array of colors.
2. Each THREE.Face() object (a list of these is in the Geometry object) will have a three-element array of colors, each of which is the color of the corresponding vertex of the face.
3. Using THREE.MeshBasicMaterial, set the vertexColors property to THREE.VertexColors. That value of that property alerts Three.js that a vertices of a face (a triangle) could have different colors.

Here's a demo that creates an RGB triangle:

Please take the time to read that code. It's not too long.

There's a function call there to TW.computeFaceColors(triGeom);. This is a function I wrote to iterate over all the triangles of a geometry, setting a property of each that is a three-element array of indices into the array of colors. The function essentially says that vertex i has color i for all i.

Here's an example with two triangles:

But what about a slightly different example, where we have two adjoining triangles, both of which have color interpolation, but where the same vertex has a different color. Here's the demo:

Notice that at the lower right we have:

• vertex B, coordinates (1,0,0), color TW.LIME
• vertex B2, coordinates (1,0,0), color TW.BLUE

Everything else in the code is the same. That is, don't think of the vertex in the lower corner as a single thing that is green for the purpose of the lower triangle and blue for the purpose of the upper triangle. Instead, simply think of it as two different vertices that happen to have the same spatial coordinates.

Subtractive Color and CMYK

Before we're done, we need to talk briefly about a few other important color models. We will have little practical use for them this semester, but you should have some familiarity with them and the concepts. The most important concept is additive versus subtractive color.

Additive color mixes light: the more, the brighter. As most people remember from kindergarten, mixing fingerpaints makes things darker. That's because paint (and ink, and so forth) works by subtracting light.

Subtractive color is used in the printing industry. The primaries are:

• Cyan or Aqua (light blue/green)
• Magenta or Fuchsia (bright pinkish/red)
• Yellow (umm, yellow)

C = 1 - R
M = 1 - G
Y = 1 - B

The 1 in the preceding equations is a vector of all 1s, so cyan = (1,1,1) - (1,0,0) = (0,1,1), which is a mixture of Green and Blue (the other two primaries). These are the additive secondaries

Theoretically, you can mix all three subtractive primaries to get black, but if you do you usually get a dark, muddy brown, so we introduce a fourth primary: black, abbreviated K.

These are collectively called CMYK. Think of the four cartridges on a color ink-jet printer.

YIQ

Color TV is broadcast in YIQ, which has intensity (luminance or brightness) as one signal (Y) and two others encode chromaticity (hue and saturation, but not respectively). So it's similar to HSL and HSV in that the black/white signal is one channel (Y), just like L and V.

Summary

• The HSV and HSL color models are often used in computer graphics because they can be a bit more intuitive and easier to work with. If you want to lighten a color but keep its hue the same, HSV and HSL make that obvious, while in RGB it's mysterious at best.
• We learned about modeling a cone as a pyramid with many faces.
• We learned about keyboard callbacks to dynamically adjust a model. Knowing about keyboard callbacks may be useful if you are building a game or other application where you want the user to interact with it, rather than just looking at it.
• The triangular faces of the color cone interpolate color across them. We looked at them mathematics of parametric equations for triangles.