Reading: Material and Lighting
The Lambert and Phong Models
In this reading, you'll learn how to create objects with different surface materials, such as dull or shiny surfaces, and how to add simple light sources to the scene. In order to render realistic looking graphical images of such scenes, we need to understand how surfaces reflect light. This process is captured in the Lambert and Phong Models.
Lighting Models
You'll notice that when we color objects directly using RGB, there is
no shading or other realistic effects. They're just cartoon
objects.
In fact, since there is no shading, it's impossible to see where two faces
meet unless they are different colors.
Lighting models are a replacement for direct color
(where we
directly specify what color something is using RGB). Instead, the actual
RGB values are computed based on properties of the object, the
lights in the scene, and so forth.
There are several kinds of lighting models used in Computer Graphics, and within those kinds, there are many algorithms. Let's first lay out the landscape, and then explore what's available in Three.js. The two primary categories of lighting are
- Global: take into account properties of the whole scene
- Local: take into account only
- material
- surface geometry
- lights (location, kind, and color)
Global lighting models take into account interactions of light with objects in the room. For example:
- light will bounce off one object and onto another, lighting it
- objects may block light from a source
- shadows may be cast
- reflections may be cast
- diffraction may occur
Global lighting algorithms fall into two basic categories, ray-tracing and radiosity algorithms:
Ray-tracing: conceptually, the algorithm traces a ray from the light source onto an object in the scene, where it bounces onto something else, then to something else, ..., until it finally hits the eye. Often the ray of light will split, particularly at clear surfaces, such as glass or water, so you have to trace two light rays from then on. Furthermore, most rays of light won't intersect the eye. For efficiency, then, algorithms may trace the rays backwards, from the eye into the scene, back towards light sources (either lights or lit objects).
Radiosity: any surface that is not completely black is treated as a light source, as if it glows. Of course, the color that it emits depends on the color of light that falls on it. The light falling on the surface is determined by direct lighting from the light sources in the scene and also indirect lighting from the other objects in the scene. Thus, every object's color is determined by every other object's color. You can see the dilemma: how can you determine what an object's color is if it depends on another object whose color is determined by the first object's color? How to escape?
Radiosity algorithms typically work by iterative improvement (successive approximation): first handling direct lighting, then primary effects (other objects' direct lighting color), then secondary effects (other objects' indirect lighting color) and so on, until there is no more change.
Global lighting models are very expensive to compute. According to Tony DeRose, rendering a single frame of the Pixar movie Finding Nemo took four hours. For The Incredibles, the next Pixar movie, rendering each frame took ten hours, which means that the algorithms have gotten more expensive even though the hardware is speeding up.
Local lighting models are perfect for a pipeline architecture like OpenGL's, because very little information is taken into account in choosing the RGB. This enhances speed at the price of quality. To determine the color of a polygon, we need the following information:
- material: what kind of stuff is the object made of? Blue silk is different from blue jeans. Blue jeans are different from black jeans.
- surface geometry: is the surface curved? How is it oriented? What direction is it facing? How would we even define the direction that a curved surface is facing?
- lights: what lights are in the scene? Are they colored? How bright are they? What directions does the light go?
Three.js manages to fall somewhere in between, because it can use the Scene Graph data structure to compute shadows, but it doesn't do the full ray-tracing or radiosity computation. We'll look at shadows later, Three.js makes them quite easy.
The rest of this reading describes local lighting models, as in Three.js.
The mathematical lighting models that are used by Three.js are the
Lambert Model
and the Phong Model.
The Phong Model is a superset
of the Lambert Model, so we'll start with the Lambert Model and then extend it
to the Phong Model. We're going to proceed in a bottom-up
fashion,
first explaining the conceptual building blocks, before we see how they
all fit together.
Local Lighting
To see a demo of what we'll be able to accomplish with material and lighting, run the lit teddy bear demo:
There are three lights that you can control: ambient light, a point light and a directional light. We'll learn more about these soon.
Material Types
Because local lighting is focussed on speed, a great many simplifications are made. Many of these may seem overly simplistic or even bizarre.
The first thing is to say that there are only three ways that light can reflect off a surface, which we'll call diffuse, specular, and translucent:
- Diffuse: These are rough surfaces, where an incoming ray of light
scatters in all directions. The result is that the direction from which
the material is viewed doesn't matter much in determining its color and
intensity. Examples:
- carpet, cloth
- dirt, rough rock
- dry grass
Look at the lit bear from different angles and you'll see that the direction from which you view a patch of brown doesn't affect the color (the brown is a diffuse material).
- Specular: These are smooth, shiny surfaces, where an incoming ray of
light might bounce, mirror-like, and proceed on. The result is that, if
the camera is lined up with the reflected rays, we'll see a bright spot
caused by that reflection. This is called a specular highlight.
Examples:
- plastic
- metal
- polished leather
Look at the lit bear's eyes, which are made from a specular material (let's imagine they are shiny glass or buttons), and you'll see a specular highlight.
- Translucent: These are surfaces that transmit as well as reflect
light. These can really only be handled properly using ray tracing.
Local lighting can do transparency after a fashion. However, we will
defer transparency for a while. Examples:
- water
- glass
- soap bubbles
So, we really only need to understand diffuse and
specular surfaces. The modeling of diffuse reflection of light
has the brightness of the surface computed by Lambert's cosine law.
See the Wikipedia article
on Lambertian
reflectance. The modeling of specular reflection uses a model by Bui
Tuong Phong and so is called
the Phong
reflection model. (Click through to this second Wikipedia entry, because
the first figure is very good.) His computation includes Lambertian as a
special case. Three.js calls these materials Lambertian
and Phong, so we will too.
Important points on the math (but we'll see more below):
-
Lambertian: we are very interested in how much the surface is facing the light: the more the surface is facing the light, the brighter it should be. Mathematically, we'll say that the cosine of the angle between two vectors:
- the surface normal (a vector that is perpendicular to the surface) and
- the light vector (a vector pointing towards the light)
the cosine tells us how "lined-up" these vectors are. The cosine is maximized at an angle of zero degrees.
-
Phong: we are also interested in how much the vector towards the eye (the camera) lines up with the vector of perfect reflection. We will again use a cosine to compute that.
Kinds of Light
In talking about kinds of material, we divided them into diffuse (Lambert) and specular (Phong). (We're not going to talk about translucent in this reading.) Of course, most materials have some of each: you get color from the diffuse properties of, say, leather, but a shine of specular highlight at the right angle.
A major part of the Phong light model, then, is light interacting with these two properties of material. The model, therefore, divides light into different kinds, so that diffuse light interacts with the diffuse material property and specular light interacts with the specular material property. It seems weird to say there are different kinds of light, but it's just to have a number corresponding to the numbers describing the materials; these numbers get multiplied together in the models.
The three kinds of light are:
- ambient
- diffuse
- specular
As we just said, the diffuse and specular light components interact with the corresponding material properties.
What is ambient
light? As you might guess from the name, it's the
light all around us. In most real-world scenes, there is lots of light
around, bouncing off objects and so forth. We can call this ambient
light: light that comes from nowhere in particular. Thus, ambient
light is indirect and non-directional. It's the local-lighting
equivalent of radiosity.
Even though in local lighting, we don't trace ambient light rays back to a specific light source, there is still a connection. This is because, in the real world, when you turn on a light in a room, the whole room becomes a bit brighter. Thus, each Three.js light source can add a bit of ambient light to the scene, brightening every object.
That ambient light interacts with the ambient
property of a
material. Because of the way it's used, a material's ambient property is
often exactly the same color as the diffuse property, but they need not
be.
Thus, each material also has the three properties: ambient, diffuse, and specular. We'll get into the exact mathematics later, but for now, you can think of these properties as colors. For example, the ambient property of brown leather is, well, brown, so that when white ambient light falls on it, the leather looks brown. Similarly, the diffuse property is brown. The specular property of the leather is probably gray (colorless), because when white specular light reflects off shiny leather, the reflected light is white, not brown.
Light Sources
In Three.js, you create a light source as an object and add it to the
scene. Lights that are part of the scene contribute to the lighting of the
objects in the scene. The lights themselves are not visible, even if the
camera is staring straight at them. Lights only manifest themselves by
illuminating objects and interacting with the objects' materials. (You
can of course, put a sphere or something at the location of a light, if
you want.) Three.js has some helper
objects that can do this for
you.
Ambient Lights
As we said above, ambient light is generalized, non-directional light that illuminates all objects equally, regardless of their physical or geometrical relationship to any light source. Thus, the location of an ambient light source is irrelevant.
In Three.js, you can create an ambient light like this;
var light0 = new THREE.AmbientLight( 0x202020 ); // 10%
This light is a very dark gray, contributing just a little brightening to the scene.
Point Sources
A common source of light in Three.js is a point source.
You can
think of it as a small light bulb, radiating light in all directions
around it. This is somewhat unrealistic, but it's easy to compute with.
To do this in Three.js, we use a THREE.PointLight:
// white light, 50% intensity, falling to zero in 80 units: var light1 = new THREE.PointLight( TW.WHITE, 0.5, 80 ); light1.position.set( 0, 10, 10 ); scene.add(light1);
Like many of the light types in Three.js, but unlike the ambient light,
a point light has an intensity. This is just a factor that the
lighting computation is multiplied by, so you can use this to make a
light brighter or dimmer. The default value of intensity (second argument
for the THREE.PointLight() constructor) is 1.
Also, point lights can attenuate with distance, so that the
intensity goes down for surfaces that are farther from the point
light. In the real world, light attenuates inversely with the square of
distance (because the light energy is spread out over the surface of a
sphere). Thus, if there were a planet that were half the distance from
the sun as the earth is, it would get four times as much solar
energy. However, years of experience in Computer Graphics has shown
that this bit of physics seems to make lights fade too quickly and so,
instead, a linear attenuation is used. The third argument to the
THREE.PointLight() constructor is the distance at which this light's
intensity attenuates to zero. In the example above, the light is at
zero intensity 80 units from the point (0,10,10), half
intensity at 40 units away, three-quarters intensity at 20 units away,
and so forth.
Lambert Model
Phong's model combines the ambient, diffuse and specular components into one big, hairy equation. We'll first address the Lambertian part of it, and then get to the Phong Model.
First, we need some notational building blocks:
- NV: the normal vector for the surface. In this context, the normal
vector is a vector that is perpendicular (or orthogonal) to
the surface. The normal vector is how we define the
orientation
of a surface — the direction it'sfacing.
The normal vector is the same over a whole plane, but may change over each point on a curved surface. The normal vector is often normalized to be a unit vector (length 1). - LV: the vector towards the light source; that is, a vector from the point on the surface to the light source (not used for ambient light). For distant lights, this vector doesn't change from point to point.
In the model, we will have parameters captured in the vector L that represent the intensity of the incoming light. We saw this in the Three.js code above. Turn them up and the light gets brighter.
We also have to worry about how much of the incoming light gets reflected. Let this be a number called R. This number is a fraction, so if R=0.8, that means that 80 percent of the incoming light is reflected. (We actually have 9 such numbers, specifying the reflection fraction for specular red, ambient green, and so on, for all 9 combinations.)
As we discussed earlier, in general, R can depend on:
- material properties: cotton is different from leather
- orientation of the surface
- direction of the light source
- distance to the light source
The light that gets reflected is the product of the incoming light intensity, L, and the fraction R:
I = L R
That is, the intensity of light that is reflected from a surface (and ends up on the image plane and the framebuffer) is the intensity of the incoming light (landing on the surface) multiplied by the reflection number.
Note that the above equation is just shorthand for the sum of 9 computations multiplying the ambient/diffuse/specular, red/green/blue light by the ambient/diffuse/specular, red/green/blue material. And that's just for one light! If we have multiple lights, we need to add up more contributions.
This leads to the problem of overdriving the lighting, where every material turns white because there's so much light falling on it. This happens sometimes in practice: you have a decently lit scene, and you add another light, and then you have to turn down your original lights (and your ambient light) to get the balance right.
Why does R depend on the light source? That is, why does the reflection fraction depend on which light we're talking about? Because the direction and distance change. But since all the light sources work the same way, we're not going to worry about which light source it is, and we'll just have our abstract Lambert Model:
I = Lamb Ramb + Ldiff Rdiff
Abstract Lambert Model
That is, the intensity of the color of an object is
- the ambient light falling on it, multiplied by the reflection amount for ambient light, plus
- the diffuse light falling on it, multiplied by the reflection amount for diffuse light.
The above equation is our abstract Lambert Model. Now let's see how to compute the two R values.
Ambient
Reflection of ambient light doesn't depend on direction or distance or orientation, so it's solely based on the material property: is the material dark or light? Note that it can be dark for blue and light for red and green. If white light falls on such a material, what does it look like? So, Ramb is a simple constant, which we will call kamb, just to remind ourselves that it's a constant:
Ramb = kamb
Note that 0 ≤ kamb ≤ 1. Why?
This constant is chosen by you the programmer as part of the material properties for an object, in the same way that you choose color. There are actually three such values, one each for red, green, and blue.
Diffuse/Lambertian
For Lambertian/diffuse surfaces, we assume that light scatters in all
directions. In lay person's vocabulary, such surfaces are often
called matte
.
However, the angle of the light does matter, because the energy (photons) is spread over a larger area. Consequently, we have
Rdiff = kdiff LV • NV
Recall that LV is the light vector, the direction to the light source, and NV is the normal vector, the orientation of the surface. The • operator is the dot product between the two vectors, described in the reading on geometry. The dot product of two normalized vectors (unit length) gives the cosine of the angle between them. Thus the meaning of this equation is that the amount of light reflected from a diffuse surface is the product of a constant, chosen by you the programmer, multiplied by the cosine of the angle between LV and NV. As before, there are actually 3 such constants, one each for red, green, and blue.
Now, we finally have our finished Lambert Model:
I = Lamb kamb + Ldiff kdiffLV • NV
Concrete Lambert Model
Lambertian Materials in Three.js
In the past, we created surfaces with THREE.MeshBasicMaterial,
which doesn't take into account the lights available in the scene. In Three.js,
you can make a
Lambertian
material like this:
var mat = new THREE.MeshLambertMaterial( {color: THREE.Color.NAMES.cyan} );
Of course, you can specify the color in many ways, as we've seen before.
The developers of Three.js decided that materials will reflect ambient light
the same way they reflect diffuse light, captured with the color
property. Using color specifications like this is a shorthand for
specifying reflection coefficients for the red, green, and blue primaries.
Phong Model
Now, let's turn to the full Phong Model by adding in specular reflections. With specular reflections, the material is (locally) smooth and is acting like a mirror. The incoming light rays bounce off the material and head off at an angle equal to their incoming angle. To understand what this means, we first need some more notational building blocks:
- EV: the vector towards the eye; that is, the Center of Projection (COP). If EV says that the surface faces away from the viewer, the surface is invisible and OpenGL can skip the calculation.
- RV: the reflection vector of the light. If the surface at that point were a shiny plane, like a mirror, RV is the direction that the light would bounce in.
The following figure illustrates these vectors:
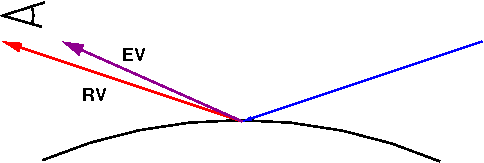
close,
the specular
highlight will be visible.
If the direction of our view, EV, is near
the reflection
direction, RV, as in the above diagram, we should see a lot of that reflected
light. This is called a specular highlight
.
Rspec = kspec (EV • RV)e
The dot product is large when the two vectors are lined up.
The e
exponent is a number that gives the shininess.
The higher the
shininess, the smaller the spotlight, because the dot product (which is
less than one), is raised to a higher power. OpenGL allows e to be
between zero and 128. In addition to e, the OpenGL programmer gets to
choose the specularity coefficient, kspec for each of red,
green, and blue. As usual, the specularity coefficient is between zero and
one.
The Complete Phong Model
Adding this last part to the Lambert Model gives us the Phong Model:
I = Lamb Ramb + Ldiff Rdiff + Lspec Rspec
Abstract Phong Model
Filling in the details of the above mathematical models, we get:
I = Lamb kamb + Ldiff kdiffLV • NV + Lspec kspec(EV • RV)e
Concrete Phong Model
Phong Materials in Three.js
All that work is to understand the following deceptively simple lines of code to set up a Phong Material in Three.js:
var mat = new THREE.MeshPhongMaterial(
{color: THREE.Color.NAMES.cyan,
specular: 0xCCCCCC,
shininess: 30});
In the example above, we used 0xCCCCCC (silver) as the
specular color. Since 0xCC is 204, and 204/255 is 0.8,
this amounts to a specularity coefficient of 80 percent, equally for
red, green, and blue. This material will reflect 80% of all specular
light falling on it.
The dot product of the reflection vector and the eye vector is raised to the 30th power, which makes this a fairly shiny object.
Summary
- There are three kinds of light: ambient, diffuse and specular
- Ambient is constant from all directions
- Diffuse depends on the angle between the light and the surface
- Specular depends on the angle between the reflected incoming light and the eye, and also depends on a scalar quantity called shininess
- In Three.js, the
colorattribute of a material captures how it interacts with diffuse and ambient light, and thespecularandshininessproperties capture the specular reflection of the surface material - In Three.js, you can have:
- Point lights
- Ambient light