Texture Mapping

Texture mapping was one of the major innovations in CG in the 1990s. It allows us to add a lot of surface detail without adding a lot of geometric primitives (lines, vertices, faces). Think of how interesting Caroline's "loadedDemo" is with all the texture-mapping.

In this reading, we'll start with a conceptual overview, quickly look at some practical examples, and then tour through the many settings, parameters, and situations there are to consider.

Conceptual View

Texture mapping paints a picture onto a polygon. Although the name is texture-mapping, the general approach simply takes an array of pixels and paints them onto the surface. An array of pixels is just a picture, which might be a texture like cloth or brick or grass, or it could be a picture of Homer Simpson. It might be something your program computes and uses. More likely, it will be something that you load from an ordinary image file, such as a JPEG.

Demos: These are all part of the 307 demos list. You need not worry about the code yet, we'll look at this later.

plane flags
These are textures that are simple arrays computed in JavaScript, which are mapped onto a plane:

• grayscale (black and white) checkerboards
• RGB checkerboards (black and red)
• grayscale US Flag
• red, white and blue US Flag

Buffy on a Plane
These are textures that are loaded from separate image files.

Conceptually, to use textures, you must do the following:

1. define a texture: a rectangular array of pixels — texels, short for texture elements. (We'll use the terms almost interchangeably, where a texel is a pixel in an array being using for texture mapping.)
2. specify a pair of texture coordinates (s,t) for each vertex of your geometry.

The graphics system "paints" the texture onto the polygon.

How it Works

Texture mapping is a raster operation, unlike any of the other things we've looked at. Nevertheless, we apply textures to 2D surfaces in our 3D model, and the graphics system has to figure out how to modify the pixels during rasterizing (AKA scan conversion).

Texture-mapping happens as part of the rasterizing process, so we'll start there.

Rasterizing

When the graphics card renders a polygon, it (conceptually)

• determines the pixel coordinates of each corner
• determines the edge pixels of the polygon, using a line-drawing program (an important one is Bresenham's algorithm, which we won't have time to study)
• determines the color of the edge pixels on a single row, by linear interpolation from the vertex colors
• walks down the row coloring each pixel, by linear interpolation from the two edge pixels

Note: standard terminology is that the polygon is called a fragment, since it might be a fragment of a Bézier surface or some such polygonal approximation to something. Thus, the graphics card applies a texture to a fragment.

This all happens either in the framebuffer (the video memory that holds the pixels that are displayed on your screen) or an array just like it.

Implementing Texture Mapping

To do texture mapping, the graphics card must

• compute a texture coordinate for each pixel during the rasterizing process, using bi-linear interpolation
• look up the texture coordinates in the array of texels, either using the nearest texel or a linear interpolation of the four nearest texels
• and either
  • use the color of the texture as the color of the pixel, or
  • combine the color of the texture with the color of the pixel

Texture Space

We can have 1D or 2D textures, though almost always 2D. The texture parameters will be in the range [0,1] in each dimension. Note that if your texture array is not square and your polygon is not square, you may have to deal with changes in aspect ratio.

Your texture is always an array and therefore is always a rectangle. Mapping a texture to rectangles is fairly easy; mapping it to other shapes is likely to cause distortion. We'll need to be careful in those cases.

Associate each vertex of our polygon with a texture parameter, just like we associate it with a normal, a color, and so forth. Three.js has properties of a Geometry object devoted to representing the texture coordinates for each vertex of a triangular face.

How do the texture coordinates relate to the 2D array of texels? This is easiest to explain with a picture such as this one:

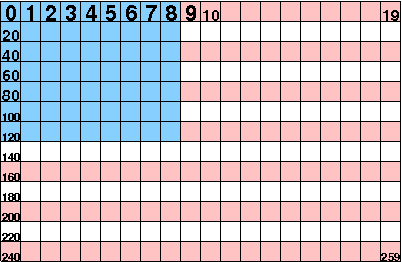
This is an array of 260 pixels, numbered from 0 to 259, arranged in a rectangular array that is 13 by 20 pixels. (Note, this is illegal in OpenGL and Three.js, because neither dimension is a power of two, but let's use it anyway.)

• As you'd expect, the first element of the texel array, that is, element [0][0] is the same as texture coordinates (0,0).
• As we go down the first row of the array, until we get to element [0][RowLength] ([0][19], which is element 19), we get to texture coordinates (1,0). This may seem odd, but it's true.
• As we go down the first column of the array, until we get to element [ColLength][0] ([12][0], which is element 240), we get to texture coordinates (0,1). Again, this may seem odd, but it's true.
• Unsurprisingly, the last element of the texel array is the corner opposite the first element, so array element [ColLength][RowLength] ([12][19], which is element 259) corresponds to texture coordinates (1,1).

Conventionally, the texture coordinates are called (s,t), just as spatial coordinates are called (x,y,z). Thus, we can say that s goes along the rows of the texture (along the "fly" of the flag). The t coordinate goes along the columns of the texture (along the "hoist" of the flag).

Although you will often use the entire texture, so that all your texture coordinates are from 0 to 1, that is not necessary. In fact, because the dimensions of texture arrays are required to be powers of two, the actual image that you want is often only a portion of the whole array.

The computed US flag array has that property. The array is 256 pixels wide by 128 pixels high, but the flag itself is 198 pixels wide by 104 pixels high. Thus, the maximum texture coordinates (if you just want the flag and none of the gray area) are:

fly	= 198/256 = 0.7734
hoist	= 104/128 = 0.8125

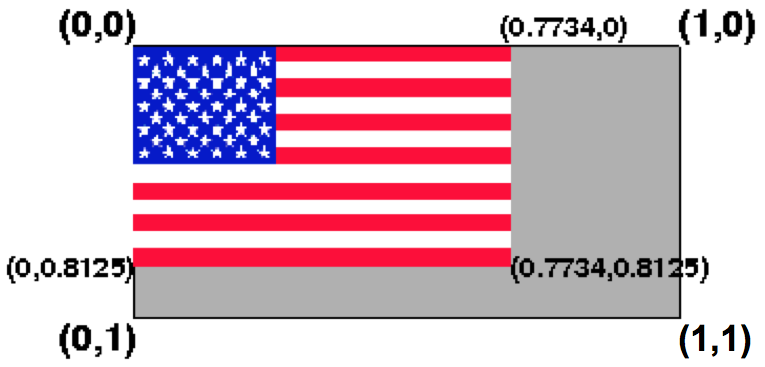
The result might look like the image above. The flag image only spans texture coordinates (s,t) from (0,0) to (0.7734,0.8125).

Of course, we also need to ensure that the rectangle we are putting the flag on has the same aspect ratio as the US flag, namely: 1.9. See the official US flag specification.

The texture parameters can also be greater than 1, in which case, we can use parameter settings to get repetitions of the texture. If s is some parameter where 0 < s < 1, specifying some part of the texture partway along, then 1+s, 2+s, and so on, are the same location in the texture. We can experiment with different values of s and t using the tutor in the next section.

Texture Tutor

Here is a basic tutor for texture mapping as we know it so far, based on a tutor by Nate Robins — experiment with the GUI controls to understand the basic concepts:

Code using Computed Textures

Let's start with texture-mapping with computed textures. Because they're computed, they'll be very simple, but we use them for two reasons:

• It reinforces the concept that a texture is just an array, and
• it avoids issues of loading an additional file and having to use an event handler

It's now time to look at the code for our first basic demo.

Here's the plane flags demo again. It's not important what's inside the code for creating checkerboards and such, but just realize that each returns an array of pixels. The most important lines of code are at the end.

The essential part of the code is shown below. Look particularly at the implementation of makeFlag(). The code below is just for

• setting up the texture
• creating the mesh

Notice that the texture is a property of the material, not the geometry. The geometry, however, defines (default) texture parameters for each vertex. (Texture parameters of individual pixels of a face are done by interpolation from the texture parameters of the face's three vertices.)

Everything else is similar to what we've seen before. View the source of the demo to get the complete program. The Three.js documentation provides more information about the THREE.DataTexture() constructor that creates the texture from the image array.

Setting Texture Coordinates

Geometry objects define texture coordinates for each vertex. Earlier, we saw that we don't always want to use the default (0,1) texture coordinates. We might want to use (0.77,0.81) as the maximum texture coordinates with the US Flag. So, how can you change the default texture coordinates (or set them on your own geometry objects)?

In Three.js, they put the texture coordinates in a property of the THREE.Geometry called faceVertexUvs (instead of using S and T, some people use U and V; both appear in the Three.js code). This property is an array of one element, and that element is an array of face uvs, where a face UV is a three-element array, corresponding to the three vertices of the face, and each element of that is a THREE.Vector2 that captures the U and V values.

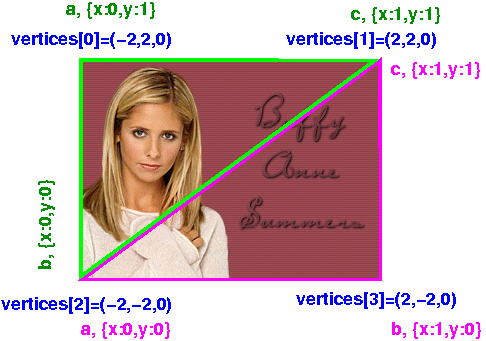
Let's try to understand this using a specific example. We'll consider the geometry object that we used to map Buffy's face onto, earlier. It's a simple 2D plane (a rectangle):

    planeGeom = new THREE.PlaneGeometry(4, 4);

Let's look inside that data structure. First, the vertices:

JSON.stringify(planeGeom.vertices)
[{"x":-2,"y":2,"z":0},   // 0
 {"x":2,"y":2,"z":0},    // 1
 {"x":-2,"y":-2,"z":0},  // 2
 {"x":2,"y":-2,"z":0}    // 3
]

Nothing too surprising there. There are four vertices, all with z=0, and the x and y values are +2 or -2. Now let's look at the two faces, with their vertices defined as indices into the array above.

> planeGeom.faces[0]
THREE.Face3 {a: 0, b: 2, c: 1, normal: THREE.Vector3, vertexNormals: Array[3]…}
> planeGeom.faces[1]
THREE.Face3 {a: 2, b: 3, c: 1, normal: THREE.Vector3, vertexNormals: Array[3]…}

So, the two triangular faces are the upper left triangle and the lower right triangle. Finally, let's look at the UV values for each of the 6 vertices (three for each of the two faces):

> JSON.stringify(planeGeom.faceVertexUvs)
[
  // array of two elements
  [
   [{"x":0,"y":1},{"x":0,"y":0},{"x":1,"y":1}],  // for face 0
   [{"x":0,"y":0},{"x":1,"y":0},{"x":1,"y":1}]   // for face 1
  ]
]

Weirdly, the two coordinates are named "x" and "y" in these objects, rather than "u" and "v" as you might expect (or even "s" and "t").

Here's a picture that might help:

Modifying the faceVertexUvs

Consider the following function, which updates the S and T values for a THREE.PlaneGeometry like we have:

Using this function, we can map our US flag onto the plane with no gray areas:

However, the code for doing this is unintuitive, because the default Three.js behavior is to flip the vertical texture parameter. This is called .flipY. So, instead of wanting the T parameter to go

• from 0 in the upper left,
• to 0.8 in the lower left

We actually set it to go

• from 0.2 = 1-0.8 in the lower left,
• to 1 in the upper left

That is, with a flipped Y, the upper left corner has coordinates of (0,1) and the lower left has coordinates of (0,0.2). To pull out just that piece, here's how we have to set the texture parameters:

  updateTextureParams(flagGeom,0,0.75,1-0.81,1);

Here's the complete demo.

Loading Images

Here's a demo showing an image file being loaded and texture-mapped onto the same plane we've used before:

Plane Buffy

The code has one very tricky part, though. When we computed an array and used it as a texture, the array was already available for rendering. With an external image, there's going to be some delay before the data arrives from some network source. This delay might run to a few hundred milliseconds, but even a few milliseconds is an enormous amount of time compared to the speed that code is running in JavaScript.

Consequently, if the only rendering we did was right after the image was referenced, the code would not work at all. Here's pseudo-code for the situation I'm describing:

var buffyTexture = new THREE.ImageUtils.loadTexture( "../../images/buffy.gif" );
var buffyMat = new THREE.MeshBasicMaterial(
    {color: THREE.ColorKeywords.white,
     map: buffyTexture});
    
var buffyMesh = new THREE.Mesh( planeGeom, buffyMat );
scene.add(buffyMesh);
TW.render();

There simply isn't time for the image to load between that first line, when a request for the image is sent to the server, and the last line, when the scene is rendered. If you try this, the plane will be blank white.

The solution is to use an event handler. Event handlers are general-purpose solutions to code that you want to run after some event has happened. In this case, the event is that the image data has finally arrived from the server. The event handler can then invoke the renderer.

The way that Three.js does this is also very standard: a callback function is passed in, and the callback will be invoked when the event occurs. Here's the improved code:

// these should be local, but we use globals so that
// you can poke around
var planeGeom, planeTex, planeMat, planeMesh;
var imageLoaded = false;

var loader = new THREE.TextureLoader();

function loadPlaneBuffy() {
    loader.load("../../images/buffy.gif",
                function (texture) {
                    console.log("buffy image is loaded");
                    imageLoaded = true;
                    planeGeom = new THREE.PlaneGeometry( 4, 4);
                    planeMat = new THREE.MeshBasicMaterial(
                           {color: THREE.ColorKeywords.white,
                            map: texture});
                    planeMesh = new THREE.Mesh( planeGeom, planeMat );
                    scene.add(planeMesh);
                    TW.render();
                });
}

In the code above, we pass in an anonymous function to be the event handler. It gets invoked when the image finishes loading, and does all the work of building the object, including its material with the texture, and finally it renders the scene. (Rendering is optional; maybe you have other objects to load first.) Nothing it does is new to you; just the packaging and timing.

That's it! Later, we will get into more complex situations where you want to use umpteen images as textures: how do you figure out that they've all, finally, loaded, and the scene can be rendered?

Coming Up

In the rest of the texture-mapping reading, we'll discuss:

• Mapping image textures onto a BoxGeometry and other shapes
• Combining texture-mapping with material and lighting. This will be very cool, allowing us to get very nice shading effects on our texture-mapped surfaces.
• Looking at using nearest versus interpolated texture values.
• The representation of textures as arrays, and the representation of images in RGB, including the concept of accessing an array in row major order.
• Bump mappings and environment mappings.

Summary

Here's what we learned

• At its most basic, a texture is an array of pixels. So is an image.
• Each vertex of a triangular face can have texture parameters
• Texture parameters are 2D and each lives in the [0,1] interval, with {0,1} being the edges of the 2D texture.
• Texture parameters outside the [0,1] interval can be
  • clamped to the edge
  • repeated
  • mirrored
• When loading textures from an image, we need to consider that it takes a non-negligible amount of time for the image to load, and so we will need to write event handlers for the after load event.