
Assignment 4
Due: Thursday, October 6

|
CS 332
Assignment 4 Due: Thursday, October 6 |
|
This assignment contains an exercise related to the MPG multi-resolution
stereo algorithm, a programming problem that involves writing a function to solve
the stereo correspondence problem using correlation, and a final problem with
some questions about the correlation-based strategy that you implemented.
Two images, chapelLeft.jpg
and chapelRight.jpg in the /home/cs332/download/stereoImages
directory will be used to test your new stereo function.
In class, we discussed a simplified version of the MPG multi-resolution stereo algorithm
and performed a hand simulation of this algorithm on the board. This problem provides
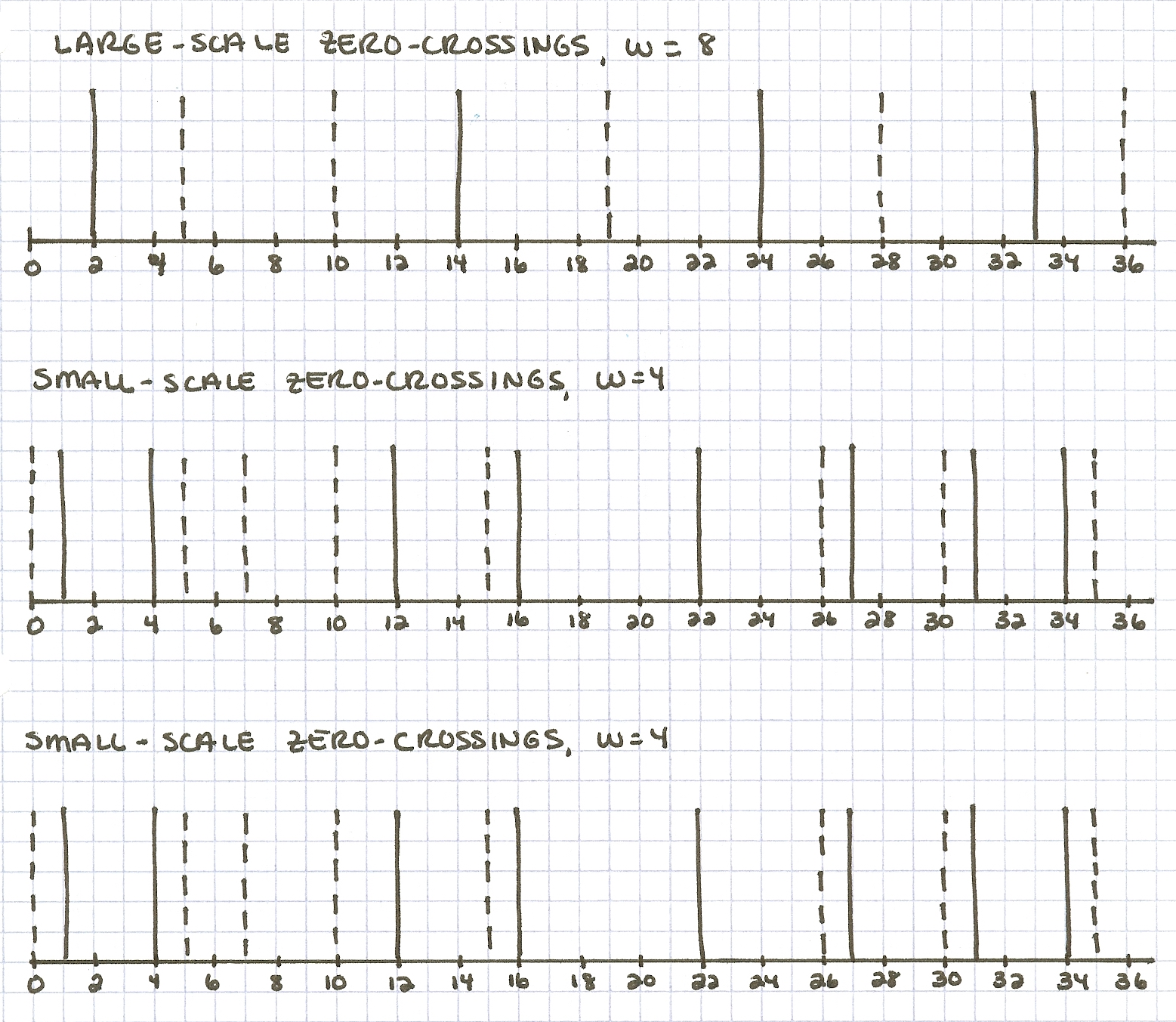
another example for you to hand simulate on your own. The zero-crossing pictures are shown
below. The top row shows zero-crossing segments obtained from a Laplacian-of-Gaussian
operator whose central positive diameter is w = 8, and the bottom two rows
show zero-crossing segments obtained from an operator with w = 4. Assume
that the matching tolerance m (the search range) is m = w/2. In
the diagram, the solid lines represent zero-crossings obtained from the left image and the
dashed lines are zero-crossings from the right image (assume that they are all zero-crossings
of the same sign). The axis below the zero-crossings indicates their horizontal position in
the image.
Part a: Match the large-scale zero-crossing segments. In your answer, indicate which left-right pairs of zero-crossings are matched and indicate their disparities.
Part b: Match the small-scale zero-crossings, ignoring the previous results from the large-scale matching. In your answer, indicate which left-right pairs of zero-crossings are matched and indicate their disparities. Show your analysis for this case on the bottom row of the figure.
Part c: Match the small-scale zero-crossings again. This time exploit the previous results from the large-scale matching. Show your analysis for this case on the middle row of the figure.
Part d: What are the final disparities computed by the algorithm, based on the matches from Part c? The final disparity is defined as the shift in position between the original location of the left zero-crossings and the location of their matching right zero-crossings.
Part e: One of the constraints that is used in all algorithms for solving the stereo correspondence problem is the continuity constraint. What is the continuity constraint, and how is it incorporated in the simple version of the MPG stereo algorithm that you hand-simulated in this problem?
In this problem, you will implement a stereo correspondence algorithm based on a strategy
known as correlation. The input for this new algorithm will be the zero-crossings
computed by the stereoZeros function used in Problem 5 of Assignment 3. In the
figure below, the top left and right pictures show a
random-dot stereogram with a central square patch that has a disparity of +2
pixels and a background disparity of +1 pixels. The middle left and right
pictures show the zero-crossings obtained from convolving the two images with a Laplacian-of-Gaussian
operator of size w = 4. Positive zero-crossings are shown in white and negative
zero-crossings in black. Your task is to write a function called stereoMatch
that solves the correspondence problem and computes a disparity for each location
in the left image. The bottom picture in the figure below shows sample results from an
implementation of stereoMatch. The function computed a disparity of
+2 for central locations in the image (displayed in white) and a disparity
of +1 for the surrounding region (displayed as gray). There is a border around
the outside of the image where disparities are not computed (zero values, shown in black).
 |  |
 |  |
 |
The figure below illustrates the strategy that you should use to solve the stereo
correspondence problem. Assume that the left and right input pictures contain the
zero-crossings derived from the original left and right stereo images. Suppose we
want to compute the disparity at location (r,c) (row r
and column c) in the left picture. Consider a square neighborhood that
extends nsize pixels in the four directions
around location (r,c), as shown in the left picture below. To compute a
disparity for this location, your function should search in the right picture for a square
patch of the same size that best matches the content of the left patch. To find the
most similar patch in the right picture, consider a range of possible horizontal positions of
the patch centered on locations (r,c-range) to (r,c+range), as
shown in the right picture below. The horizontal position of the most similar patch in the
right image, relative to the position of the original patch in the left image, determines
the disparity assigned to location (r,c). This basic strategy is similar to
the one that was implemented for the fingerprint-matching extra credit problem in Assignment 2,
but in this case, there is only a horizontal shift of the patch between the left and right
patterns.

In the case of fingerprint matching, a measure that was described as the "sum of squared
differences" was used to assess the similarity of two image patches. For this problem, you
will use a different measure based on correlation. Correlation is a general
computational technique that arises in many image processing applications and in the
description of models for biological computations. Correlation is similar to convolution.
The picture below shows two small image patches labeled I1 and
I2
that each contain the three values -1, 0 and +1 (similar to a
zero-crossing representation):
The correlation between the two image patches is defined as:
where the summation is performed over the entire 2D region. The values in the two patches are multiplied point-by-point and the products are then summed. For the above images, the pointwise multiplication yields the following intermediate result:
The sum of all of these products is 6. In this simple case where the images
contain only -1, 0 and +1, the pointwise product will be
1 at a location where both image patches contain +1 or both
image patches contain -1. If the two patches contain opposite values at the
same location (i.e. -1 and +1), their product will be
-1. If we now think of the +1 and -1 values in the
input left and right patterns as
representing positive and negative zero-crossings, then this correlation measure effectively
adds up the number of locations that contain zero-crossings of the same sign in the
two image patches, and subtracts the number of locations that contain zero-crossings of
opposite sign in the two patches. Thus, this correlation measure gives a rough indication
of how well the zero-crossings match between two image patches. As the similarity of the
zero-crossings in the two patches increases, the correlation increases. Therefore a patch
in the right pattern that best matches a given patch in the left pattern will have the
maximum correlation value.
As stated earlier, your task is to define a function stereoMatch that uses the
approach described above to solve the stereo correspondence problem. Your function should
have the following header:
function result = stereoMatch (zcleft, zcright, nsize, range)
zcleft and zcright contain the zero-crossings computed with the
stereoZeros function. nsize is the neighborhood size (the results
shown above were computed with nsize = 10), and range is a
positive number that represents the range of disparities considered. The result
matrix should contain double type values and be the same size as the input
zero-crossing matrices. This function should compute a disparity value for every location
where the square neighborhood in the left and right patterns fits within the bounds of
the matrix.
Your stereoMatch function can be stored in your copy of the
/home/cs332/download/stereo subdirectory. Create a script file that contains
a sequence of statements that create a stereogram, use the conv2D function to
convolve the left and right images with a Laplacian-of-Gaussian operator (a value of
w = 4 works well), compute the zero-crossings with the stereoMatch
function, run your stereoMatch function to compute disparities, and
display the results. You can use random-dot stereograms to test your function initially,
for example, the "wedding cake" random-dot stereogram created in the stereoScript.m
code file used in Assignment 3. This script file also contains sample code for the convolution
and zero-crossing steps, which you used for Problem 5 of Assignment 3. Add code to your script
to call your stereoMatch function. When displaying the resulting disparity map with
imshow or imtool, be sure to specify the range of values in the matrix,
e.g. imshow(result, [-2 2]). When your function is complete, add code to your
script to run your stereoMatch function on the zero-crossings obtained from the
stereo image pair chapelLeft.jpg and chapelRight.jpg in the
/home/cs332/download/stereoImages directory.
An operator size of w = 4, disparity range of 6 and neighborhood size
of 10 should produce good results (remember to use this new disparity range when
calling imshow or imtool to display your results). These images can be
loaded into MATLAB using the imread function, for example:
>> left = imread('chapelLeft.jpg');
This stereo pair is constructed from a real image and a disparity pattern that
conveys a secret message that you can view. 
Part a: We discussed four constraints that most stereo correspondence algorithms incorporate: uniqueness, similarity, continuity and the epipolar constraint. Explain how the correspondence-based strategy that you implemented in Problem 2 uses each of these four constraints.
Part b: Using the ideas that were embodied in the multi-resolution stereo algorithms developed by Marr, Poggio and Grimson, describe how the correlation-based stereo algorithm could be modified to use multiple spatial scales. You can either consider the ideas embodied in the original multi-resolution stereo algorithm proposed by Marr and Poggio to account for the use of multiple spatial scales and eye movements in human stereo processing, or the simplified version of the Marr-Poggio-Grimson multi-resolution algorithm that you hand-simulated in Problem 1. You do not need to implement anything here, just describe a possible strategy in words.
Submission details: Hand in a hardcopy of your answers to Problems 1 and 3,
and a hardcopy of your final stereoMatch.m and script code files. Drop off an
electronic copy of your code files by logging into puma,
connecting to your stereo folder and executing the following command:
submit cs332 assign4 *.*