Assignment 9: SMT 1

In this assignment, you will:

This is a pair assignment—you may choose to either complete the assignment alone or with one other CS340 classmate. On Gradescope, you will be able to form a group with maximum size 2.

Setup

Programming language

This assignment uses the z3 SMT solver as a library in Python (Python 3, specifically). Follow the instructions from class to install the z3 library on your local machine.

Create two new files, problems.py and README.{md, txt}. There is no stencil code for this assignment.

Output format

For this first SMT assignment, just printing the results returned by the z3 library is sufficient (though you should only print a returned instance if one exists).

Additional resources

Here are references for the z3 interface and Python API.

Problem 1

Alice thinks that there might be some non-negative number whose negation is also non-negative.

Create two functions named non_negative_negation_int and non_negative_negation_bitvec to find such a number, if it exists, for both the theory of integers and the theory of bitvectors. For the theory of bitvectors, use a 32-bit bitvector, like C's int type.

Written Q1 In your README, either answer that no such number exists or provide the number. For the bitvector number, provide your answer in hex with the correct number of bits for its size.

Hint: recall that Python has a built-in hex() function that you can use (either in your file or in the Python interpreter) to convert numbers to hex.

Problem 2

Using her insight from the previous problem, Alice wonders if she can apply some hacker's delight bit-twiddling to implement a ternary conditional for C integer types without the using the ? operator.

She write the following C code:

// Try to implement x ? y : z with bit-twiddling
int wacky_conditional(int x, int y, int z) {
   int i = ((-x|x) >> 31);
   return (y & i) | (z & ~i);
}

Create a new function, wacky_conditional, and use z3 to determine whether or not Alice's conditional representation is equivalent to x ? y : z.

Written Q2 In your README, say whether or not Alice's function is equivalent. In your own words, describe why the SMT constraints your wrote answer the equivalence question for any 32-bit x, y, and z.

Written Q3 What have you proven about Alice's implementation?

Hint: the ternary operator in Python's z3 library is named If (but it requires the first argument to be a boolean).

Problem 3

A NAND (not and) logical gate is a commonly-used low-level circuit building block because is a universal gate that can be implemented efficiently with a small number of transistors.

One of the following two circuits correctly implements XOR (exclusive or) using NAND gates and NOT gates.

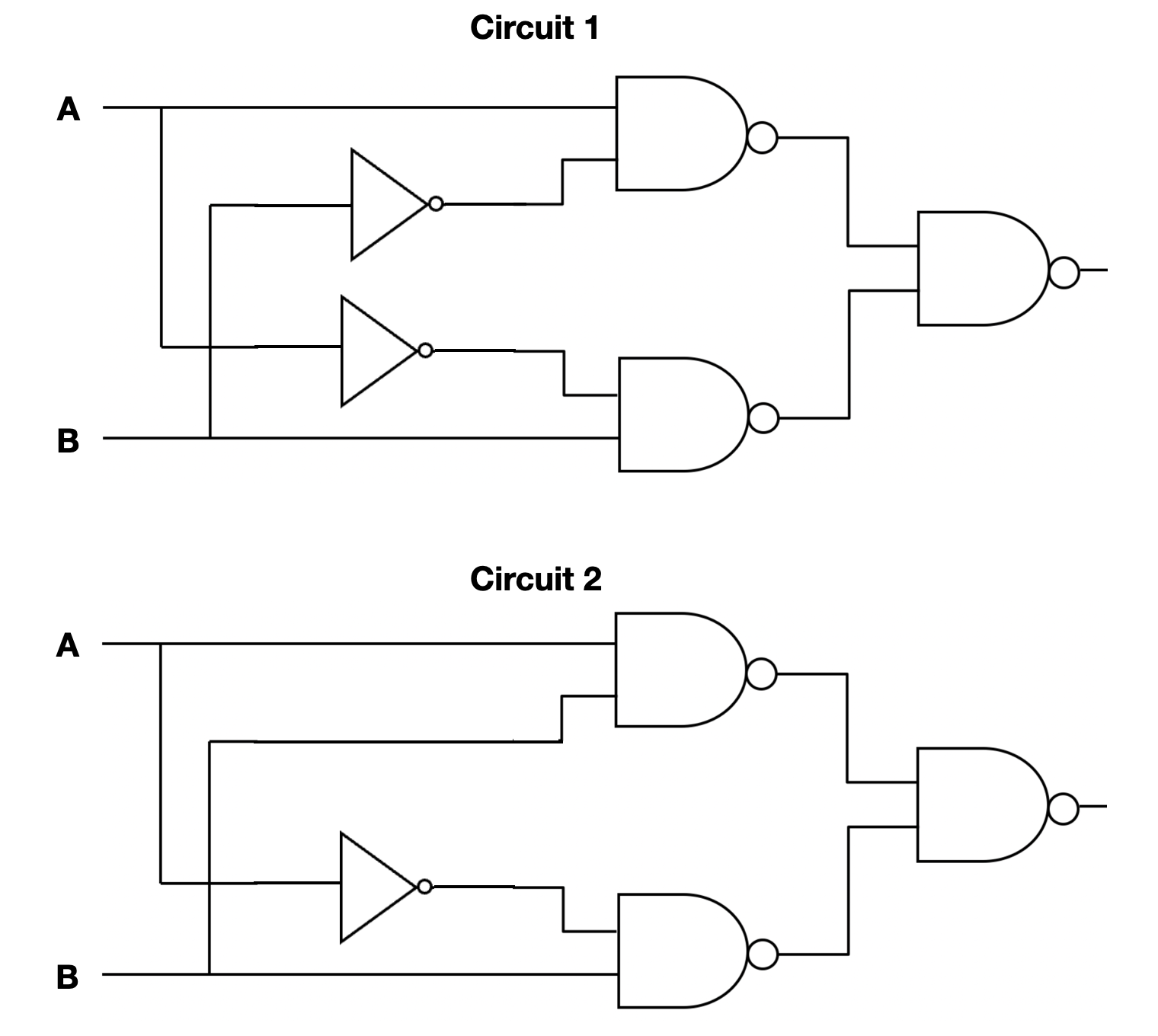
Screenshot 2024-04-02 at 11.46.39 PM

Create two functions, nand_circuit1 and nand_circuit2, and use z3 to show that one circuit is equivalent to XOR and one circuit is not equivalent to XOR.

Written Q4 In your README, say which circuit is equivalent. For the circuit that is not equivalent, describe a concrete counterexample and explain what the expected result is and what the circuit incorrectly produces instead.

Hint: z3 does not have NAND built in, but you can model it with Not(And(..., ...).

Problem 4

Three integers (x,y,z) form a Pythagorean triple if they are positive and x2+y2=z2. A way to produce Pythagorean triples is Euclid’s formula. Euclid's formula states that given integers m and n such that m>n>0, (x,y,z)=(m2−n2,2mn,m2+n2) is a Pythagorean triple.

Part 1

Write a new function, verify_euclid, to verify Euclid's formula using the theory of mathematical integers. Verifying the formula means showing that for any choice of m and n, the computed (x,y,z) is a Pythagorean triple.

If your solution is taking a long time (over a minute) to run, you may want to try adding additional constraints. Make sure you have constraints representing each part of the definition of Pythagorean triples and Euclid’s formula as described above.

Part 2

A triple (x,y,z) is primitive if and only if x, y, and z share no common factors (other than 1).

Write a new function, non_primitive, to check whether Euclid's formula can produce non-primitive triples.

Written Q5 In your README, state whether Euclid's formula can produce non-primitive triples (providing a concrete example if applicable).

Grading

In your README, also report:
Written Q6: Collaborators other than your partner?
Written Q7: Roughly how long did this assignment take you (in hours)?

This assignment is worth 100 points, broken down by:

Submission

Submit the following files on Gradescope: problems.py and README.{txt, md}.

Attribution

Question 4 is based on a previous version of the SMT assignment from Tim Nelson's Logic for Systems at Brown University.