Bias in AI

Readings

Group Discussion:

[What are the sources of bias in AI systems?
What kinds of bias appear in these systems?]{.standout}

Group Discussion:

[Who is responsible for harm done by an AI system?]{.standout}

Group Discussion:

[If you were a movie villain, how would you use ostensibly harmless/helpful AI to do evil?]{.standout}

Bias

Data Science

“Data science” sometimes skips a step and creates a model directly from data.

Theory-free Models

Models and Authority

Regression

Regression

A regression line showing the error of several data points 

Regression

If we have n data points (xi, yi), our error is:

$E = \sum_{i=1}^{i=n} \sqrt{(y_i - f(x_i))^2}$

We can find an analytical minimum if our
function f is simple, like f(x) = mx + b.

Gradient Descent

  1. Take the derivative of our error function with respect to the constants in that function, $\frac{\delta E}{\delta C}$.
  2. Nudge those constants in the direction that reduces the error.
  3. Repeat until we get to zero error (or a minimum).

Newton’s method illustrated, with a curve and a point on that curve. From that point, a tangent line is drawn which creates another point where it crosses zero, and from that point, we go back up to the curve, and then draw another tangent line which intersects zero closer to where the curve does. 

Several regression lines in gray leading towards a blue regression line that’s a better fit with some data points. 

Overfitting

A very curvy line that goes through a set of data points exactly, compared to a straight line which isn’t exact but keeps going in the same direction as the data does at the ends. 

Deep Learning

Videos

Core Concept

Training

A Neural Network


yj = f(∑iwj, i ⋅ xi)


$$ \left[ \begin{matrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{matrix} \right] = f \left( \left[ \begin{matrix} w_{1,1} & w_{2,1} & \cdots & w_{n,1}\\ w_{1,2} & w_{2,2} & \cdots & w_{n,2}\\ \vdots & \vdots & \ddots & \vdots \\ w_{1,m} & w_{2,m} & \cdots & w_{n,m}\\ \end{matrix} \right] \cdot \left[ \begin{matrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{matrix} \right] \right)$$

Network Structure

Sigmoid


$$ f(x) = \frac{1}{1 + e^{-kx}} $$

A sigmoid function{height=9em}

Deep Networks

Example Target Function

Input (x) Output (y)     Input (x) Output (y)
A cat{style=“height:120px”} [1, 0] A dog{style=“height:120px”} [0, 1]

What does it learn?

Video excerpt{target=“blank”}

What does it need?

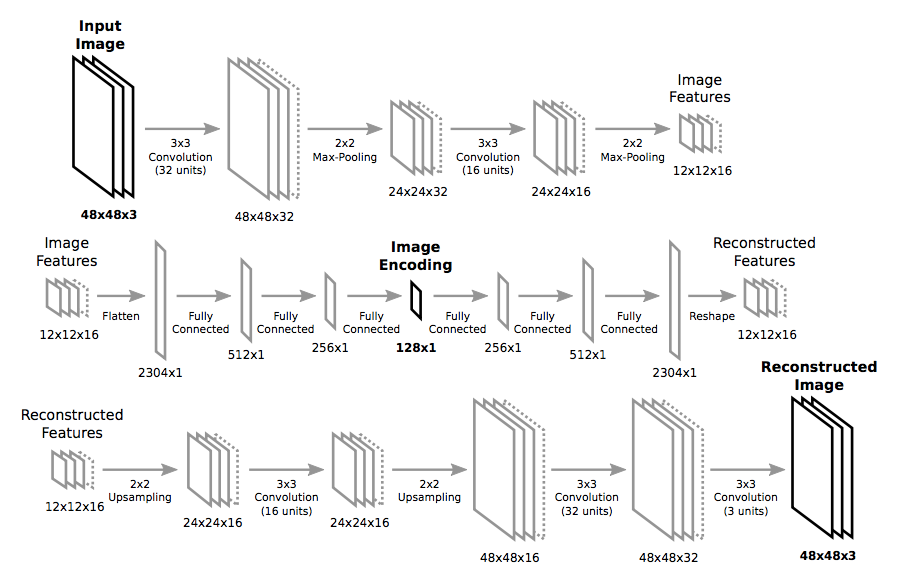
Autoencoding

Applications

Applications

Discussion

[How might biases affect these applications of deep learning?]{.standout}

[How should we feel about deep learning and AI as a scientific project?]{.standout .fragment}

My Work

Computational Creativity

Critical (Computational) Creativity

Past Projects

Measuring “novelty” using an auto-encoder network.

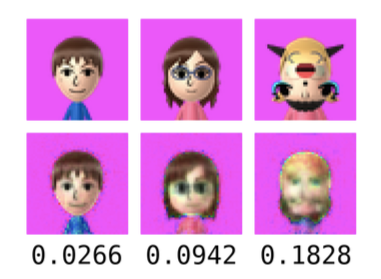
Three Mii images with blurred versions beneath each. On the left, a brown-haired man close to the default settings, in the middle, a woman wearing glasses, and on the right, some kind of alien with eyes and mouth transposed. The blurred versions of the left two faces look similar to their base images, but the right face’s blurred image is very different. 

A lineup of different Mii images by novelty, showing four examples from each bin as well as an average for eight bins from left to right. The examples are mostly more similar to the default Mii on the left and less similar on the right. 

A network structure diagram for a symmetric convolutional autoencoder network with two convolutional layers and three fully connected layers. 

Bonus

Convolutional Networks

Convolutional Network Explanation

Recurrent Networks

LSTM Explanation