Incremental Noise

Perlin & Simplex Noise

Black and white simplex noise 
Screenshot from No Man’s Sky demo with trees, grass, and cliffs{width=80%} 
[from --verbose blog and IGN]{.attribution}

Noise Algorithms

 

input coordinates → pseudo-random process → noise

 

Incremental Processes

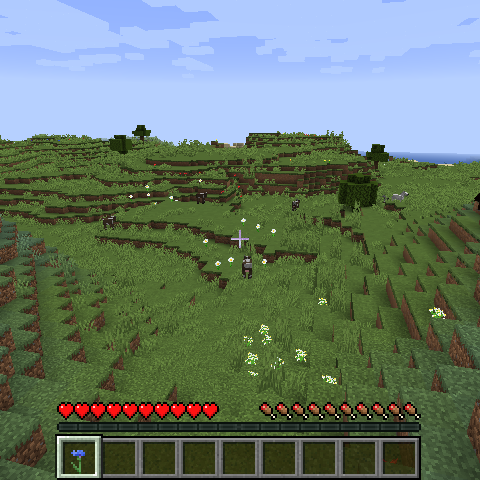
A valley in Minecraft{width=320} 

[Caveat: narratives of exploration/exploitation are harmful.]{.fragment .standout}

Incremental & Irreversible

A forest fire caused by lava near trees{width=320} 

Shuffling for Guarantees

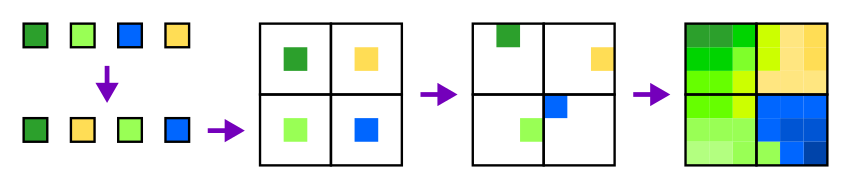Diagram showing four colors being shuffled and then assigned to a 2x2 grid, with a final step that blurs between them.{width=100%} 

Diagram showing two sets of 50 10x10 regions. In the top set, each region is white, with some blue and red pixels, sometimes very few, sometimes more. In the bottom half, each region is white with exactly 1 red pixel and 5 blue ones. The colored pixels are scattered in different positions in all cases.{.pixelated width=50%} 

What if… ?

Anarchy

Core Features

Reversible PRNG

# standard PRNG
next = prng(seed)
# anarchy
next = prng(prev, seed)
prev = rev_prng(next, seed)

Why go Backwards?

Reversible Shuffling

Reversible Shuffling

A diagram showing how several simple reversible operations are composed to create a reversible shuffle the appears unpredictable.{width=50%} 

Reversible Shuffling

# standard shuffle
a = [0, 1, 2, 3, 4]
random.shuffle(a) # operates in-place

# anarchy
for i in [0, 1, 2, 3, 4]:
  sh = anarchy.cohort_shuffle(i, 5, seed)
  assert(
    i == anarchy.rev_cohort_shuffle(sh, 5, seed)
  )

Reversible Shuffling

Reversible Distribution

Solution: divide N items among S segments of size C, with α roughness.

Reversible Distribution

distribution_portion(s, N, S, C, α, seed)

# reversible:
distribution_segment(i, N, S, C, α, seed)

# incremental:
distribution_prior_sum(s, N, S, C, α, seed)

A diagram showing how items are recursively divided along with slots to create an assignment.{width=100%} 

A similar diagram showing how the two sets of divisions are matched to each other.{width=50%} 

Distribution Algorithm

  1. Compute half of segments and random split point for items.
  2. Pick first or second part:
    • If asking about an item, compare index to item split point.
    • If asking about a segment, compare to halfway point.
  3. Recurse in first or second part with fewer segments
    (and probably fewer items).
    • Stop if there is only one segment.

Distribution Algorithm

Combined Capabilities

Why Use Anarchy?

Why Use Anarchy?

Demo

https://solsword.github.io/words

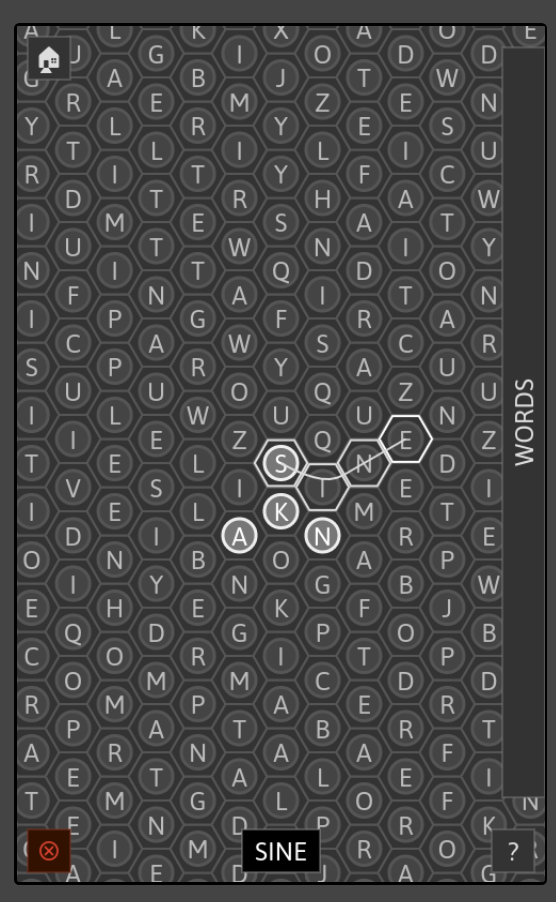Hexagonal grid where each space contains a letter, and words can be found. The word sine is selected.{width=30%}  The same grid, with words highlighted in different colors. The word Bangkok is selected. A red outline shows the shape of a hexagon within the grid that is four grid-units on each side.{width=30%} 

Words Game

Quality

Limitations

Anarchy vs. Mersenne Twister

PRNG

anarchy
White-noise-like image (scattered white black and gray pixels) visualizing 10000 random values from anarchy.{width=6em .pixelated} A star-like image with a black background and isolated white and gray pixels. Each pixels shows how many random numbers for that column of the image were followed by a random number in that column.{width=6em .pixelated} 
random
Random values from Python’s built-in random function, visualized as with the values from anarchy.{width=6em .pixelated} Star-like image created using Python’s built-in random using the same method as the image for anarchy.{width=6em .pixelated} 

Shuffle

anarchy
Image with four regions. At the top, 20 rows showing repeated shuffles of the same list, and 20 showing different shuffles of an initial list. At the bottom on the left, a darkish-gray random grayscale region visualizing relative frequencies of how often each input position ends up at each output position. At the bottom on the right, a gray square with a black diagonal and some faintly lighter horizontal and vertical stripes. This represents how often items in a given initial position (by row) end up in front of items from another initial position (by column) and would ideally be perfectly flat gray.{width=8em .pixelated} 
random
Another image with the same layout and general appearance as the image for anarchy. Differences include a noticeably brighter bottom-left region, and a slightly flatter gray bottom-right region.{width=8em .pixelated}

Distribution

An image with four regions organized vertically. At the top, 20 lines showing different distributions of 50 items across 10 10-item bins. Below that, 7 groups of 5 lines each showing random distributions that get progressively rougher. The first group is all completely even distributions, and the last is very chaotic. Below that, ten rows where each pixel represents a bin and the color is how full it is, appearing generally gray with lighter and darker regions. Finally, another region with the same meaning, but where there are distinct very bright and dark patches (due to higher roughness).{width=50% .pixelated} 

Bonus Demo

Log-time Incremental Algorithms

https://solsword.github.io/labyrinfinite