PS2: Antics with Semantics
- Due: 6pm Friday 16 September (but there’s also the default 24-hour grace period).
- Notes:
- You can do Problems 1, 2, 3 (and possibly 4) based on knowledge you already have.
- The problems needn’t be done in order. Feel free to jump around.
- There is no solo problem on this pset, so you can collaborate on them with your classmates following the usual Gilligan’s Island rule.
- Submission:
- In the yourFullName CS251 Spring 2016 Folder that you created for PS1, create a Google Doc named yourFullName CS251 PS2.
- For Problems 1, 2, 3, and 5, include all answers in your PS2 google doc. Please format your evaluation derivations in Problem 4 so that they’re easy to read. Format the derivation using the fixed-width Courier New font (can use a small font size if that helps).
- For Problem 4 (Racket Recursion):
- Copy the contents of
yourAccountName-ps2-functions.rktto the Google Doc. Format the definitions using the fixed-width Courier New font (can use a small font size if that helps). - Drop a copy of your
yourAccountName-ps2-functions.rktin your~/cs251/drop/ps02drop folder on cs.wellesley.edu.
- Copy the contents of
1. Language Wars (25 points)
Read the paper The Programming Language Wars by Andreas Stefik and Stefan Hanenberg and answer the following questions in your writeup.
-
Briefly summarize the key ideas in the paper.
-
The authors list numerous Research Questions (RQ). Pick the three you think are most important, and explain why. Are there any you think are unimportant?
-
The authors list numerous Responsibilities (Resp.) for inviduals and communities in the area of programming languages. Pick the three you think are most important, and explain why. Are there any you think are unimportant?
-
What do you think Stefik and Hanenberg would think of Paul Graham’s Revenge of the Nerds essay you read for PS1? Justify your answer.
-
Is there anything you disagree with in the paper? If so, explain.
2. The Evils of Two Lesses (12 points)
Consider the exact expression 3 < 4 < 2. (Do not add any extra parens or move around any symbols.) This expression is handled differently in different programming languages. For each of the following four programming languages, explain how this expression is handled in that language.
-
If the expression returns a value, specify that value and explain why that value is returned and how you know this fact.
-
If the expression causes an error, explain the nature of the error (is it a syntax error? type error? something else?) and how you know this fact.
- Java
- JavaScript
- Python
- Racket
3. Truthiness (18 points)
 )
)
In the context of a conditional test, a value that chooses the then arm of the conditional is called truthy and a value that chooses the else arm of the conditional is called falsey (sometimes spelled falsy). We will use the term neither to refer to a value that cannot be used as a conditional test (causing a compile-time or run-time error).
We have seen that in Racket, the #f value is falsey and every value that is not #f is truthy; Racket has no neither values. This problem asks you to explore truthiness in other languages.
Below are four programming languages and links to their language specification documents. Based on information in the documents, determine which values are truthy, which are falsey, and which (if any) are neither. In your answers, explicitly cite all the section of the reference manuals that you used to determine your answer.
-
JavaScript (a.k.a. EcmaScript): http://www.ecma-international.org/publications/files/ECMA-ST/Ecma-262.pdf
-
C: http://www.open-std.org/JTC1/SC22/WG14/www/docs/n1570.pdf
Notes:
-
Hint: begin by searching for the terms if statement or conditional in the documents.
-
One of the purposes of this problem is to introduce you to language specification documents. These are the authoritative sources for answering any questions about the languages, even nit-picky ones. Although they can be somewhat dense, you should get into the habit of consulting them. For reasons you will understand after doing this problem, people who write/consult/cite such language specifications are sometimes called language lawyers.
-
In the EcmaScript specification, notions like ReturnIfAbrupt and CompletionRecord are used to model the dynamic semantics of exceptions and can be ignored for the purposes of this problem.
-
The C specification for the semantics of if statments uses the terminolgy “compares equal to 0”. Although it’s not obvious, this terminology is defined in Section 6.5.9 Equality operators on p. 96.
4. Racket Recursion (15 points)
Although you’ve written recursive function definitions before in other courses, recursion is particularly important in CS251 for three reasons:
-
The list data structures in Racket and Standard ML are recursively defined, and so are naturally processed with recursion. (You will get lots of practics with these starting next week.)
-
Neither Racket nor Standard ML has looping constructs, so what you would express via loops in other languages must be expressed via recursion in these languages. (We’ll see that a particular kind of recursion known as tail recursion can express anything expressible with loops in other languages and then some.)
-
Later in the semester we will study metaprograms – i.s., programs that manipulate other programs. Metaprograms typically process the abstract syntax tree (AST) structure of the program being manipulated. Such tree processing is most naturally expressed using recursion. Indeed, you’ve already seen that big-step evaluation semantics is recursive in nature.
For each of the following Racket function specifications, write and test a recursive function that satisfies that specification. In all of your definitions, you should use the following recursive problem solving strategy:
-
For which argument(s) is the function so simple that the answer can be returned immediately? This is the base case.
-
For the other case(s) (known as the recursive case(s)), use divide/conquer/glue:
-
divide: make one or more subproblems that are smaller instances of the given problem;
-
conquer: assume that the recursive function you’re defining simply works and returns the correct answer on all of the smaller problems.
-
glue: combine the result(s) of the recursive function call(s) with information in the original problem to create the correct result for the whole problem.
-
The fact, fib, sum-between and sum-between-halves functions shown above are all instances of this strategy, and we will see many examples of recursion with list arguments in the coming week. (The sum-between-iter function is not an instance of this strategy because it introduces a helper function that changes the structure of the problem into an iteration.)
Notes:
-
For this problem, you should use Dr. Racket to create a single file named
yourAccountName-ps2-functions.rktthat contains all the functions (including helper functions) that you define for this problem. -
In your definitions, unless otherwise instructed, you should not introduce any recursive helper functions. (But you can define nonrecursive helper functions).
-
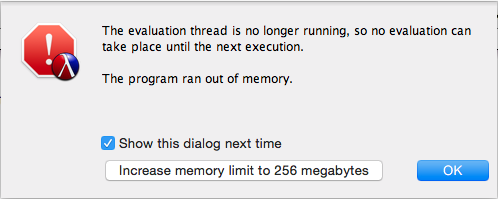
If the following error message pops up during the testing of one of your functions, it mostly likely means that you have an infinite recursion that doesn’t reach its base case and runs out of memory due to a stack depth that cannot fit into available memory.
-
(8 points) Define a function
sum-squares-of-ints-divisible-bythat takes three integer arguments (divisor,lo, andhi) and returns the sum of the squares of all the integers betweenloandhi(inclusive) that are evenly divisible bydivisor.> (sum-squares-of-ints-divisible-by 2 1 8) 120 ; = 2^2 + 4^2 + 6^2 + 64^2 > (sum-squares-of-ints-divisible-by 3 1 10) 126 ; = 3^2 + 6^2 + 9^2 > (sum-squares-of-ints-divisible-by 5 1 10) 125 ; = 5^2 + 10^2 > (sum-squares-of-ints-divisible-by 7 1 10) 49 ; = 7^2 > (sum-squares-of-ints-divisible-by 11 1 10) 0 ; no multiples of 11 between 1 and 10 > (sum-squares-of-ints-divisible-by 11 7 15) 121 ; = 11^2 > (sum-squares-of-ints-divisible-by 2 10 8) 0 ; the range "from 10 up to 8" is emptyUse the following helper function, which is helpful in this problem and some of the following ones.
(define divisible-by? (lambda (num divisor) (= (remainder num divisor) 0))) -
(7 points) A Hamming number is any positive integer expressible as 2i⋅3j⋅5k. E.g., the Hamming numbers between 1 and 100 are:
1 2 3 4 5 6 8 9 10 12 15 16 18 20 24 25 27 30 32 36 40 45 48 50 54 60 64 72 75 80 81 90 96 100Define a function
hamming?that takes a single numeric argument (including 0, negatives, and nonintegers), and returns#tif the argument is a Hamming number and#fif it is not. Your function need not work on arguments that are not numbers.> (hamming? 30) #t > (hamming? 31) #f > (hamming? -31) #f > (hamming? 3.141) #f > (hamming? 0) #f > (filter hamming? (range -100 101)) ; list all integers from -100 up to (but not including 101) ; for which hamming? is true '(1 2 3 4 5 6 8 9 10 12 15 16 18 20 24 25 27 30 32 36 40 45 48 50 54 60 64 72 75 80 81 90 96 100)Notes:
- Use
integer?to test if a value is an integer. - Use
(and e1 e2 ... en)to determine if all of the expressionse1,e2, …,enare true. - Use
(or e1 e2 ... en)to determine if at least one the expressionse1,e2, …,enis true. - You needn’t use any
ifexpressions in your definition. All you need areandandor. (But you can useifif you want to.) - The
divisible-by?helper function from above is useful.
- Use
5. Sum Fun (30 points)
In class, we defined the following recursive factorial function:
(define fact
(lambda (n)
(if (= n 0)
1
(* n (fact (- n 1))))))We can use the small-step semantics introduced in lecture on Tue. Sep 13 to explain the evaluation of (fact 4). To simplify things, let’s introduce the abbreviation λ_fact for the follow lambda expression:
(lambda (n) (if (= n 0) 1 (* n (fact (- n 1)))))Then here is the small-step evaluation derivation for (fact 4):
(fact 4)
⇒ (λ_fact 4)
⇒ (if (= 4 0) 1 (* 4 (fact (- 4 1))))
⇒ (if #f 1 (* 4 (fact (- 4 1))))
⇒ (* 4 (fact (- 4 1)))
⇒ (* 4 (λ_fact (- 4 1)))
⇒ (* 4 (λ_fact 3))
⇒ (* 4 (if (= 3 0) 1 (* 3 (fact (- 3 1)))))
⇒ (* 4 (if #f 1 (* 3 (fact (- 3 1)))))
⇒ (* 4 (* 3 (fact (- 3 1))))
⇒ (* 4 (* 3 (λ_fact (- 3 1))))
⇒ (* 4 (* 3 (λ_fact 2)))
⇒ (* 4 (* 3 (if (= 2 0) 1 (* 2 (fact (- 2 1))))))
⇒ (* 4 (* 3 (if #f 1 (* 2 (fact (- 2 1))))))
⇒ (* 4 (* 3 (* 2 (fact (- 2 1)))))
⇒ (* 4 (* 3 (* 2 (λ_fact (- 2 1)))))
⇒ (* 4 (* 3 (* 2 (λ_fact 1))))
⇒ (* 4 (* 3 (* 2 (if (= 1 0) 1 (* 1 (fact (- 1 1)))))))
⇒ (* 4 (* 3 (* 2 (if #f 1 (* 1 (fact (- 1 1)))))))
⇒ (* 4 (* 3 (* 2 (* 1 (fact (- 1 1))))))
⇒ (* 4 (* 3 (* 2 (* 1 (λ_fact (- 1 1))))))
⇒ (* 4 (* 3 (* 2 (* 1 (λ_fact 0)))))
⇒ (* 4 (* 3 (* 2 (* 1 (if (= 0 0) 1 (* 0 (fact (- 0 1))))))))
⇒ (* 4 (* 3 (* 2 (* 1 (if #t 1 (* 0 (fact (- 0 1))))))))
⇒ (* 4 (* 3 (* 2 (* 1 1))))
⇒ (* 4 (* 3 (* 2 1)))
⇒ (* 4 (* 3 2))
⇒ (* 4 6)
⇒ 24To highlight the essential steps of such an evaluation, we will often use the notation e1 ⇒* e2 to mean that expression e1 rewrites to expression e2 by some number (possibly zero) of ⇒ steps, and then omit all lines except for the ones involving (1) calls to λ_fact on argument values or (2) calculation of the final result. Here’s an example of an abbreviated evaluation derivation for the above example:
(λ_fact 4)
⇒* (* 4 (λ_fact 3))
⇒* (* 4 (* 3 (λ_fact 2)))
⇒* (* 4 (* 3 (* 2 (λ_fact 1))))
⇒* (* 4 (* 3 (* 2 (* 1 (λ_fact 0)))))
⇒* (* 4 (* 3 (* 2 (* 1 1))))
⇒ (* 4 (* 3 (* 2 1)))
⇒ (* 4 (* 3 2))
⇒ (* 4 6)
⇒ 24As another example, consider a recursive definition of a function for calculating the nth Fibonacci number:
(define fib
(lambda (n)
(if (<= n 1)
n
(+ (fib (- n 1)) (fib (- n 2))))))Suppose λ_fib is an abbreviation for the following lambda expression:
(lambda (n)
(if (<= n 1)
n
(+ (fib (- n 1)) (fib (- n 2))))))Then here is an abbreviated evaluation derivation for (fib 4)
(λ_fib 4)
⇒* (+ (λ_fib 3) (fib (- 4 2)))
⇒* (+ (+ (λ_fib 2) (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ (+ (λ_fib 1) (fib (- 2 2))) (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ (+ 1 (λ_fib 0)) (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ (+ 1 0) (fib (- 3 2))) (fib (- 4 2)))
⇒* (+ (+ 1 (λ_fib 1)) (fib (- 4 2)))
⇒* (+ (+ 1 1) (fib (- 4 2)))
⇒* (+ 2 (λ_fib 2))
⇒* (+ 2 (+ (λ_fib 1) (fib (- 2 2))))
⇒* (+ 2 (+ 1 (λ_fib 0)))
⇒* (+ 2 (+ 1 0))
⇒ (+ 2 1)
⇒ 3Note that (λ_fib 4) ⇒* (+ (λ_fib 3) (fib (- 4 2))) and not (λ_fib 4) ⇒* (+ (λ_fib 3) (λ_fib 2)). Why? Because the small-step evaluation of (+ e1 e2) must fully evaluate e1 to a value v1 before any evaluation is performed on e2. So the expression (fib (- 4 2)) is not simplified in any way until (λ_fib 3) evaluates to 2.
In this problem you are asked to reason about and create such abbreviated derivations.
a. Alternative if semantics (3 points)
The small-step reduction rules for if expressions in Racket are
(if V_test E_then E_else) ⇒ E_then, ifV_testis a value that is not#f[if nonfalse](if #f E_then E_else) ⇒ E_else[if false]
Lois Reasoner thinks that the reduction of if expressions should be changed to:
(if V_test V_then V_else) ⇒ V_then, ifV_testis a value that is not#f[if nonfalse Lois](if #f V_then V_else) ⇒ V_else[if false Lois]
These differ from the actual rules by requiring that all three subexpressions e_test, e_then, and e_false of (if e_test e_then e_false) are first evaluated to values before the if expression can be simplified.
Explain that Lois’s alternative semantics for if are a bad idea. For example, what would happen in the evaluation of (fact 4) if Lois’s rules were used?
b. sum-between (4 points)
Here is a definition of a sum-between function that returns the sum of all the integers between its two integer arguments (inclusive):
(define sum-between
(lambda (lo hi)
(if (> lo hi)
0
(+ lo (sum-between (+ lo 1) hi)))))Using the abbreviated small-step derivation notation shown above for (fact 4), show an abbreviated evaluation derivation for (sum-between 3 7) that shows the key steps in this derivation. Use the notation λ_sb as an abbreviation for the lambda expression
(lambda (lo hi)
(if (> lo hi)
0
(+ lo (sum-between (+ lo 1) hi))))Your derivation should only show lines in which λ_sb is called on values and lines involving the calculation of + in (+ lo ..., but not any lines that involve if, >, or the calculation of + in (+ lo 1).
c. Stack depth for sum-between (3 points)
Although the small-step evaluation model does not have any explicit notion of stack frames, operations like * in the recursive fact definition and + in the recursive sum-between definition correspond to pending operations that are remembered to be performed when control returns the stack frame for a particular function invocation in a model based on stack frames. In the (fact 4) example, the fact that the maximal sequence of nested multiplications, (* 4 (* 3 (* 2 (* 1 1)))), has four multiplications corresponds to a nesting of five stack frames (one for each call of fact on arguments 4 down to 0).
In the case of fact, we will call the maximal number of pending multiplications the stack depth. So (fact 4) has a stack depth of 4, and (fact 100) would have a stack depth of 100. So the stack depth of (fact n) grows linearly in n.
Let’s define the stack depth for sum-between to be the maximal number of nested pending addition operations in the small-step evaluation derivation.
-
What is the stack depth for
(sum-between 3 7)? -
What is the stack depth for
(sum-between 1 128)? -
How does the stack depth for
(sum-between 1 n)grow withn?
d. sum-between-halves (9 points)
Here is a definition of a sum-between-halves function that also returns the sum of all the integers between its two integer arguments (inclusive), but does so in a different way from sum-between:
(define sum-between-halves
(lambda (lo hi)
(if (> lo hi)
0
(if (= lo hi)
lo
(+ (sum-between-halves lo (quotient (+ lo hi) 2))
(sum-between-halves (+ 1 (quotient (+ lo hi) 2)) hi))))))Show an abbreviated evaluation derivation for (sum-between-halves 3 7) that shows the key steps in this derivation. Use the notation λ_sbh as an abbreviation for the lambda expression
(lambda (lo hi)
(if (> lo hi)
0
(if (= lo hi)
lo
(+ (sum-between-halves lo (quotient (+ lo hi) 2))
(sum-between-halves (+ 1 (quotient (+ lo hi) 2)) hi))))))Your derivation should be similar to the (fib 4) example given above. Note that somes lines will have a mixture of calls to λ_sbh on values and calls to sum-between-halves on unevaluated expressions. See the (fib 4) example for an explanation of this. For example, your derivation should begin like this:
(λ_sbh 3 7)
⇒* (+ (λ_sbh 3 5)
(sum-between-halves (+ 1 (quotient (+ 3 7) 2)) 7))
⇒* (+ (+ (λ_sbh 3 4)
(sum-between-halves (+ 1 (quotient (+ 3 5) 2)) 5))
(sum-between-halves (+ 1 (quotient (+ 3 7) 2)) 7))e. Stack depth for sum-between-halves (5 points)
Define the stack depth for a call to sum-between-halves as the maximal number of nested pending + operations from (+ (sum-between-halves ...) (sum-between-halves ...)).
-
What is the stack depth for
(sum-between-halves 3 7)? -
What is the stack depth for
(sum-between 1 128)? -
How does the stack depth for
(sum-between-halves 1 n)grow withn? -
Does
sum-between-halvesoffer any benefit oversum-betweenas a way to calculate the sum of integers in a range?
f. sum-between-iter (4 points)
Now we consider one more way to calculate the sum of integers in a given range. The function sum-between-iter defined below also sums numbers in a given range using the helper function sum-between-tail.
(define sum-between-iter
(lambda (lo hi)
(sum-between-tail lo hi 0)))
(define sum-between-tail
(lambda (lo hi sum-so-far)
(if (> lo hi)
sum-so-far
(sum-between-tail (+ lo 1) hi (+ lo sum-so-far)))))Show an abbreviated evaluation derivation for (sum-between-iter 3 7) that shows the key steps in this derivation. Use the notation λ_sbi as an abbreviation for the lambda expression
(lambda (lo hi)
(sum-between-tail lo hi 0)))and the notation λ_sbt as an abbreviation for the lambda expression
(lambda (lo hi sum-so-far)
(if (> lo hi)
sum-so-far
(sum-between-tail (+ lo 1) hi (+ lo sum-so-far)))))In your derivation, show only lines in which λ_sbi or λ_sbt are called on values.
g. Benefits of sum-between-iter/sum-between-tail (2 points)
Do sum-between-iter/sum-between-tail offer any benefit(s) over sum-between and sum-between-halves? Explain.