PS5: Trees and Programs
- Due: Friday, March 18. This is a soft deadline. But try to finish it before break because PS6 will be posted after break and will be due on Fri. Apr. 1.
- Notes:
- Currently, the Racket problems (Problems 1, 2, and 3) are complete, but the SML problems (Problems 4 and 5) are still under development.
- This pset has 100 points.
- It has been designed in such a way that you can expect 10 points to require approximately 1 hour. Please let me know if this expectation is wrong on particular problems!
- Please keep track of the time estimates for each problem/subproblem.
- Submission:
- In the yourFullName CS251 Spring 2016 Folder that you created for PS1, create a Google Doc named yourFullName CS251 PS5.
- For each problem and subproblem, please indicate at the beginning of each writeup approximately how long that problem took you to solve and write up.
- You will create six code files in this pset:
- Problem 1a:
yourAccountName-scoping.rkt - Problem 1b:
yourAccountNameScoping.py - Problem 2:
yourAccountName-sexp.rkt - Problem 3:
yourAccountName-ps5-postfix.rkt - Problem 4:
yourAccountName-pairs.sml - Problem 5:
yourAccountName-TTTreeFuns.sml
- Problem 1a:
- Include all answers, including copies of code from your
.rkt,.py, and.smlfiles in your PS5 Google Doc. - Drop copies of your
.rkt,.py, and.smlfiles in your~/cs251/drop/ps05drop folder on cs.wellesley.edu.
1. Naming and Scope (15 points)
As seen in the lecture on Naming and Scoping (slides 9-8 through 9-15 and 9-25 through 9-26 in these slides), (1) the same name can be declared in several different scopes and (2) names can be consistenly renamed as long as they do not changed the “connection” between references and declarations. In this problem you will rename each declaration of a given name by suffixing the name with distinct “subscripts” that begin with an underscore, and consistently rename all uses to maintain the meaning of the program. For example, given the following set of definitions
(define n 17)
(define (f x) (+ x n))
(define (x f)
(let {[x (f x)]}
(x f)))a consistent renaming with numeric subscripts is
(define n_1 17)
(define (f_1 x_1) (+ x_1 n_1))
(define (x_2 f_2)
(let {[x_3 (f_2 x_2)]}
(x_3 f_2)))while a consistent renaming with textual subscripts is:
(define n_top 17)
(define (f_top x_ftop) (+ x_ftop n_top))
(define (x_top f_xtop)
(let {[x_let (f_xtop x_top)]}
(x_let f_xtop)))-
(7 points) The following contrived collection of Racket definitions can be found here. Create a copy of this file named
yourAccountName-scoping.rkt. In this file, perform consistent renaming with subscripted names as described above.(define (f a b) (if (< a b) b (+ (let {[f (λ (b c) (f c (- b (g a))))] [g (λ (a) (g (+ a b)))] [a (let* {[a (f a (- b 1))] [b (f a b)] [f (λ (a c) (* a (+ b c)))]} (f (g a) b))] [b (+ a b)]} (f (g b) a)) (f (g a) (- b 1))))) (define (g a) (letrec {[f (λ (b c) (g (- a (+ b c))))] [g (λ (a) (if (< a b) a (f a b)))]} (define (g a) (* a c)) (define c (+ a b)) (f b (g c)))) (define (h b) (+ a b)) (define a 17) (define b (h a))Notes:
-
The original top-level definiton of
fdid not make sense and has been fixed. -
Although this problem has many details, once you understand the scoping rules, it should be straightforward.
-
Please use textual subscripts that are easy to understand.
-
You may use Dr. Racket’s feature for highlighting the connections between declarations and references to help you check your solution, but should not use it to initially create your solution.
-
-
(8 points) The following contrived collection of Python definitions can be found here. Create a copy of this file named
yourAccountNameScoping.py. In this file, perform consistent renaming with subscripted names as described above.x = 1 y = 2 z = 3 def p(x,y): return z*(x + y) def q(z): global y if z <= 0: return y else: x = p(y,z) y = 1 + q(z - x) return z - x*y def r(x): def p(y,z): global x def q(y): global z def r(z): global y x = z + 1 y = y + 2 return x*y x = r(y) y = x + z z = y + z return z if y < z: return z else: x = q(y) y = r(x) z = x*y return p(-z, y) y = 2*x x = q(x) z = p(x,y) return z def test_r(): global x,y,z x=1 y=2 z=3 return map (lambda i: (i, r(i)), range(-10,11))Note:
-
Please use textual subscripts that are easy to understand.
-
If your renaming is correct, invoking
test_r()should give the following result:
[(-10, 36), (-9, 156), (-8, 492), (-7, 1296), (-6, 3072), (-5, 6828), (-4, 14580), (-3, 30360), (-2, 62232), (-1, 126324), (0, 254892), (1, 2), (2, 4), (3, 6), (4, 8), (5, 10), (6, 12), (7, 14), (8, 16), (9, 18), (10, 20)] -
2. Deep Reverse (10 points)
We saw in lecture that tree recursion on trees represented as s-expressions could be expressed rather elegantly. For example:
(define (atom? x)
(or (number? x) (boolean? x) (string? x) (symbol? x)))
(define (num-atoms sexp)
(if (atom? sexp)
1
(foldr + 0 (map num-atoms sexp))))
> (num-atoms '((a (b c) d) e (((f) g h) i j k)))
11
> (num-atoms '(a b c d))
4
> (num-atoms 'a)
1
> (num-atoms '())
0
(define (atoms sexp)
(if (atom? sexp)
(list sexp)
(foldr append null (map atoms sexp))))
> (atoms '((a (b c) d) e (((f) g h) i j k)))
'(a b c d e f g h i j k)
> (atoms '(a b c d))
'(a b c d)
> (atoms 'a)
'(a)
> (atoms '())
'()In this problem, you will define a function (deep-reverse sexp) that returns a new s-expression in which the order of the children at every node of the s-expression tree sexp is reversed.
> (deep-reverse '((a (b c) d) e (((f) g h) i j k)))
'((k j i (h g (f))) e (d (c b) a))
> (deep-reverse '(a b c d))
'(d c b a)
> (deep-reverse 'a)
'a
> (deep-reverse '())
'()Notes:
-
Begin with this starter file sexp.rkt, which you should rename to
yourAccountName-sexp.rkt. Add your definition ofdeep-reverseto this file. -
Your definition should have form similar to the defintions for
num-atomsandatoms, but you’ll want to use something other thanfoldr.
3. Extending PostFix (30 points)
In lecture we studied an interpreter for the PostFix language implemented in Racket. This pset includes two versions of this interpreter:
-
ps5-postfix-without-errors.rkt is a version that does not handle any error checking.
-
ps5-postfix.rkt is a version that implements error checking
Review the code in these two files before beginning this problem.
In this problem, you will be experimenting with the second interpreter. Begin by making a copy of ps5-postfix.rkt named yourAccountName-ps5-postfix.rkt and load this into Dr. Racket. Near the bottom of this file is the following PostFix program named sos (for “sum of squares”). Racket’s semi-colon comments have been used to explain the commands in the program:
;; Sum-of-squares program
(define sos
'(postfix 2 ; let's call the arguments a and b, from top down
1 nget ; duplicate a at top of stack
mul ; square a
swap ; stack now has b and a^2 from top down
1 nget mul ; square b
add ; add b^2 + a^2 and return
))Let’s run the program on the arguments 5 and 12:
> (postfix-run sos '(5 12))
after executing 1, stack is (1 5 12)
after executing nget, stack is (5 5 12)
after executing mul, stack is (25 12)
after executing swap, stack is (12 25)
after executing 1, stack is (1 12 25)
after executing nget, stack is (12 12 25)
after executing mul, stack is (144 25)
after executing add, stack is (169)
169Note that the stack that results from executing each command on the previous stack is displayed, line by line. This behavior is controlled by the print-stacks? flag at the top of the program:
(define print-stacks? #t)If we set the flag to #f, the intermediate stack display will be turned off:
(define print-stacks? #f)> (postfix-run sos '(5 12))
169Turn the print-stacks? flag on when it’s helpful to understand or debug a PostFix program.
-
(10 points)
Consider the following Racket function
gthat is defined near the bottom of the PostFix intepreter file:(define (g a b c) (- c (if (= 0 (remainder a 2)) (quotient a b) (* a (+ b c)))))In this part, your goal is to flesh out the definition of a three-argument PostFix program
pfgthat performs the same calculation asgon three arguments:(define pfg '(postfix 3 ;; Flesh out and comment the commands in this PostFix program ))Here are some examples with a correctly defined
pfg. (Earlier versions incorrectly usedapply f ...below instead of the correctapply g ....)> (apply g '(10 2 8)) 3 > (postfix-run pfg '(10 2 8)) 3 > (apply g '(-7 2 3)) 38 > (postfix-run pfg '(-7 2 3)) 38Notes:
-
Please comment the commands in
pfglike those insos. -
You have been provided with a testing function
(test-pfg)that will test yourpfgfunction on 4 sets of arguments:;; Tests on an incorrect definition of pfg: > (test-pfg) Testing pfg on (10 2 8): ***different results*** f: 3 pfg: -3 Testing pfg on (11 2 8): ***different results*** f: -102 pfg: 102 Testing pfg on (-6 3 8): ***different results*** f: 10 pfg: -10 Testing pfg on (-7 2 3): ***different results*** f: 38 pfg: -38 ;; Tests on a correct definition of pfg: > (test-pfg) Testing pfg on (10 2 8): same result for f and pfg = 3 Testing pfg on (11 2 8): same result for f and pfg = -102 Testing pfg on (-6 3 8): same result for f and pfg = 10 Testing pfg on (-7 2 3): same result for f and pfg = 38
-
-
(5 points) Extend PostFix by adding the following three commands:
leis likelt, but checks “less than or equal to” rather than “less than”geis likegt, but checks “greater than or equal to” rather than “greater than”andexpects two integers at the top of the stack. It replaces them by 0 if either is 0; otherwise it replaces them by 1.
For example:
> (postfix-run '(postfix 0 4 5 le) '()) 1 > (postfix-run '(postfix 0 5 5 le) '()) 1 > (postfix-run '(postfix 0 5 4 le) '()) 0 > (postfix-run '(postfix 0 4 5 ge) '()) 0 > (postfix-run '(postfix 0 4 4 ge) '()) 1 > (postfix-run '(postfix 0 5 4 ge) '()) 1 > (postfix-run '(postfix 0 0 0 and) '()) 0 > (postfix-run '(postfix 0 0 1 and) '()) 0 > (postfix-run '(postfix 0 1 0 and) '()) 0 > (postfix-run '(postfix 0 0 17 and) '()) 0 > (postfix-run '(postfix 0 17 0 and) '()) 0 > (postfix-run '(postfix 0 1 1 and) '()) 1 > (postfix-run '(postfix 0 1 17 and) '()) 1 > (postfix-run '(postfix 0 17 17 and) '()) 1 > (postfix-run '(postfix 0 17 23 and) '()) 1Notes:
-
Do not modify
postfix-exec-commandfor this part. Instead, just add three bindings to the listpostfix-relops. -
The testing function
(test-3b)will test all ofle,ge, andandin the context of the single PostFix programtest-sorted:(define test-sorted '(postfix 3 ; let's call the arguments a, b, and c, from top down 2 nget le ; is a <= b? 3 nget 3 nget ge ; is c >= b? and ; is a <= b and c >= b? )) > (test-3b) ; Uses the test-sorted program in its definition Trying test-sorted on (4 5 6): works as expected; result = 1 Trying test-sorted on (4 5 5): works as expected; result = 1 Trying test-sorted on (4 4 5): works as expected; result = 1 Trying test-sorted on (4 4 4): works as expected; result = 1 Trying test-sorted on (4 6 5): works as expected; result = 0 Trying test-sorted on (5 6 4): works as expected; result = 0 Trying test-sorted on (5 4 6): works as expected; result = 0 Trying test-sorted on (6 5 4): works as expected; result = 0 Trying test-sorted on (6 4 5): works as expected; result = 0 Trying test-sorted on (5 5 4): works as expected; result = 0 Trying test-sorted on (5 4 4): works as expected; result = 0
-
(5 points) Extend PostFix with a
dupcommand that duplicates the top element of the stack (which can be either an integer or executable sequence). For example:(define sos-dup '(postfix 2 dup mul swap dup mul add)) > (postfix-run sos-dup '(3 4)) after executing dup, stack is (3 3 4) after executing mul, stack is (9 4) after executing swap, stack is (4 9) after executing dup, stack is (4 4 9) after executing mul, stack is (16 9) after executing add, stack is (25) 25 (define cmd-dup '(postfix 1 (dup dup mul add swap) dup 3 nget swap exec exec pop)) > (postfix-run cmd-dup '(4)) after executing (dup dup mul add swap), stack is ((dup dup mul add swap) 4) after executing dup, stack is ((dup dup mul add swap) (dup dup mul add swap) 4) after executing 3, stack is (3 (dup dup mul add swap) (dup dup mul add swap) 4) after executing nget, stack is (4 (dup dup mul add swap) (dup dup mul add swap) 4) after executing swap, stack is ((dup dup mul add swap) 4 (dup dup mul add swap) 4) after executing dup, stack is (4 4 (dup dup mul add swap) 4) after executing dup, stack is (4 4 4 (dup dup mul add swap) 4) after executing mul, stack is (16 4 (dup dup mul add swap) 4) after executing add, stack is (20 (dup dup mul add swap) 4) after executing swap, stack is ((dup dup mul add swap) 20 4) after executing exec, stack is ((dup dup mul add swap) 20 4) after executing dup, stack is (20 20 4) after executing dup, stack is (20 20 20 4) after executing mul, stack is (400 20 4) after executing add, stack is (420 4) after executing swap, stack is (4 420) after executing exec, stack is (4 420) after executing pop, stack is (420) 420 > (postfix-run '(postfix 0 dup) '()) ERROR: dup requires a nonempty stack ()Notes:
-
Implement
dupby adding acondclause topostfix-exec-command. -
Test your
dupimplementation using the above test cases. Yourdupimplementation should ensure there is at least one value on the stack, and give an appropriate error message when there isn’t.
-
-
(10 points) In this part you will extend PostFix with a
rotcommand that behaves as follows. The top stack value should be a positive integer rotlen that we’ll call the rotation length. Assume there are n values v1, …, vn below rotlen on the stack, where n is greater than or equal to rotlen. Then the result of performing therotcommand is to rotate the top rotlen elements of the stack by moving v1 after vrotlen. I.e., the order of values on the stack afterrotshould be v2, …, vrotlen, v1, vrotlen+1, …, vn. So the first rotlen elements of the stack have been rotated by one unit, while the order of the remaining elements on the stack is unchanged.Here are examples involving
rot:(define rot-test '(postfix 6 4 rot 3 rot 2 rot)) > (postfix-run rot-test '(8 7 6 5 9 10)) after executing 4, stack is (4 8 7 6 5 9 10) after executing rot, stack is (7 6 5 8 9 10) after executing 3, stack is (3 7 6 5 8 9 10) after executing rot, stack is (6 5 7 8 9 10) after executing 2, stack is (2 6 5 7 8 9 10) after executing rot, stack is (5 6 7 8 9 10) 5 > (postfix-run '(postfix 3 (mul add) rot) '(5 6 7)) after executing (mul add), stack is ((mul add) 5 6 7) ERROR: rot length must be a positive integer (mul add) > (postfix-run '(postfix 3 -1 rot) '(5 6 7)) after executing -1, stack is (-1 5 6 7) ERROR: rot length must be a positive integer -1 > (postfix-run '(postfix 3 4 rot) '(5 6 7)) after executing 4, stack is (4 5 6 7) ERROR: not enough stack values for rot (4 5 6 7)Notes:
-
Implement
rotby adding acondclause topostfix-exec-command. -
Racket supplies a
list-tailfunction that is very helpful for implementingrot:> (list-tail '(10 20 30 40 50) 0) '(10 20 30 40 50) > (list-tail '(10 20 30 40 50) 1) '(20 30 40 50) > (list-tail '(10 20 30 40 50) 2) '(30 40 50) > (list-tail '(10 20 30 40 50) 3) '(40 50) > (list-tail '(10 20 30 40 50) 4) '(50) > (list-tail '(10 20 30 40 50) 5) '()Racket does not provide a similar
list-headfunction, but I have provide that in the.rktfile. It works this way:> (list-head '(10 20 30 40 50) 0) '() > (list-head '(10 20 30 40 50) 1) '(10) > (list-head '(10 20 30 40 50) 2) '(10 20) > (list-head '(10 20 30 40 50) 3) '(10 20 30) > (list-head '(10 20 30 40 50) 4) '(10 20 30 40) > (list-head '(10 20 30 40 50) 5) '(10 20 30 40 50) -
Test your
rotimplementation using the above test cases. Yourrotimplementation should give appropriate error messages in various situations, like those in the test cases.
-
4. Pair Generation Revisited (20 points)
In this problem, you will translate Racket functions that are solutions to the pair generation problem (Problem 4) of PS4 into corresponding SML functions. Since you are already given the implementations, your focus is on SML syntax and types rather than on algorithms.
Write all of your SML code in a file named yourAccountName-pairs.sml.
-
pairs_hof(8 points) Translate the Racketrangeandpairs-hoffunctions into SMLrangeandpairs_hoffunctions:(define (range lo hi) (if (<= hi lo) null (cons lo (range (+ 1 lo) hi)))) (define (pairs-hof n) (foldr append '() (map (λ (len) (map (λ (start) (cons start (+ start len))) (range 0 (- (+ n 1) len)))) (range 1 (+ n 1)))))For example:
val range = fn : int -> int -> int list val pairs_hof = fn : int -> (int * int) list - range 0 10; val it = [0,1,2,3,4,5,6,7,8,9] : int list - range 3 8; val it = [3,4,5,6,7] : int list - range 5 5; val it = [] : int list - Control.Print.printLength := 100; - pairs_hof 5; val it = [(0,1),(1,2),(2,3),(3,4),(4,5),(0,2),(1,3),(2,4),(3,5),(0,3),(1,4),(2,5), (0,4),(1,5),(0,5)] : (int * int) listNotes:
-
If you haven’t done so already, read these notes on SML/NJ and Emacs SML Mode and follow the advice there. In particular, it is strongly recommended that you create an SML interpreter within a
*sml*buffer in Emacs. Then you can useM-pandM-nto avoid retyping your test expressions. -
Because hyphens are not allowed in SML identifiers, you should translate all hyphens in Racket identifiers to underscores. E.g.,
pairs-hofin Racket becomespairs_hofin SML. -
Be careful with your explicit parenthesis in SML. Many type errors in SML programs come from incorrectly parenthesizing expressions.
-
foldrandmapare both built into SML:val foldr = fn: ('a * 'b -> 'b) -> 'b -> 'a list -> 'b val map = fn: ('a -> 'b) -> 'a list -> 'b list -
Racket’s
appendtranslates to SML’s infix@operator, but when you want to pass it as an argument to a first-class function you write it asop@. -
In this entire problem (not just this part) some instances of Racket’s
conswill translate to SML’s infix list-prepending operator::, while some will translate to the tupling notation(<exp1>, <exp2>)for pair creation. Reason about SML types to figure out which to use when. SML’s type checker will yell at you if you get it wrong. -
Control.Print.printLengthcontrols how many list elements are displayed; after this number, ellipses are used. For example:- Control.Print.printLength := 5; val it = () : unit - range 0 20; val it = [0,1,2,3,4,...] : int list - Control.Print.printLength := 20; val it = () : unit - range 0 20; val it = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19] : int listAnother such control is
Control.Print.printDepth, which controls printing in nested lists. You won’t need that here, but might in the future.
-
-
pairs_genlist(7 points) Translate the Racketgenlistandpairs-genlistfunctions into SMLgenlistandpairs_genlistfunctions:(define (genlist next done? seed) (if (done? seed) null (cons seed (genlist next done? (next seed))))) (define (pairs-genlist n) ; Assume n a positive integer (genlist (λ (pair) (if (= (cdr pair) n) (cons 0 (+ 1 (- (cdr pair) (car pair)))) ; increase the diff (cons (+ 1 (car pair)) (+ 1 (cdr pair))))) (λ (pair) (> (cdr pair) n)) (cons 0 1)))For example:
val genlist = fn : ('a -> 'a) -> ('a -> bool) -> 'a -> 'a list val pairs_genlist = fn : int -> (int * int) list - genlist (fn x => x + 1) (fn x => x > 10) 1; val it = [1,2,3,4,5,6,7,8,9,10] : int list - pairs_genlist 5; val it = [(0,1),(1,2),(2,3),(3,4),(4,5),(0,2),(1,3),(2,4),(3,5),(0,3),(1,4),(2,5), (0,4),(1,5),(0,5)] : (int * int) listNotes:
-
SML does not allow
?in identifiers, so translatedone?tois_doneorisDone -
Use pattern matching on tuples when translating the
(λ (pair) ...)functions. Translate these to something like(fn (fst,snd) => ...).
-
-
pairs_iter(5 points) Here is a version of the Racketpairs-iterdefinition from the PS4 Problem 4d solutions in which thepairs-diff-tailandpairs-start-tailhelper functions are defined internally rather than a top level. This allows omitting some paremeters in their definitions:(define (pairs-iter n) (define (pairs-diff-tail diff result) (define (pairs-start-tail start result) (if (< start 0) (pairs-diff-tail (- diff 1) result) (pairs-start-tail (- start 1) (cons (cons start (+ start diff)) result)))) (if (< diff 1) result ;; Immediately return list of all pairs when reach base case (pairs-start-tail (- n diff) result))) (pairs-diff-tail n (list)))Translate this definition of
pairs-iterinto an SMLpairs_iterfunction. For example:val pairs_iter = fn : int -> (int * int) list - pairs_iter 5; val it = [(0,1),(1,2),(2,3),(3,4),(4,5),(0,2),(1,3),(2,4),(3,5),(0,3),(1,4),(2,5), (0,4),(1,5),(0,5)] : (int * int) listNotes:
-
Like Racket, SML uses tail recursion to express iteration rather than using looping constructs.
-
Your definition should flesh out the following skeleton:
fun pairs_iter n = let fun pairs_diff_tail diff result = let fun pairs_start_tail start result = (* body of pairs_start_tail goes here *) in (* body of pairs_diff_tail goes here *) end in (* body of pairs_iter goes here *) end
-
5. 2-3 Trees (25 points)
In this problem you will use SML to implement aspects of 2-3 trees, a particular search tree data structure that is guaranteed to be balanced.
Begin by skimming pages 1 through 7 of this handout on 2-3 trees. (I create this handout for CS230 in Fall, 2004, but we no longer teach 2-3 trees in that course).
In a 2-3 tree, there are three kinds of nodes: leaves, 2-nodes, and 3-nodes. Together, these can be expressed in SML as follows:
datatype TTTree = (* 2-3 tree of ints *)
L (* Leaf *)
| W of TTTree * int * TTTree (* tWo node *)
| H of TTTree * int * TTTree * int * TTTree (* tHree node *)For simplicity, we will only consider 2-3 trees of integers, though they can be generalized to handle any type of value.
For conciseness in constructing and displaying large trees, the three constructors have single-letter names. For example, below are the pictures of four sample 2-3 trees from the handout and how they would be expressed with these constructors:
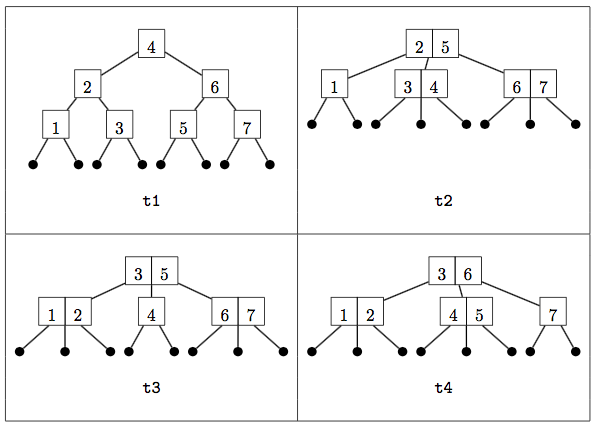
val t1 = W( W(W(L,1,L), 2, W(L,3,L)), 4, W(W(L,5,L), 6, W(L,7,L)))
val t2 = H( W(L,1,L), 2, H(L,3,L,4,L), 5, H(L,6,L,7,L))
val t3 = H( H(L,1,L,2,L), 3, W(L,4,L), 5, H(L,6,L,7,L))
val t4 = H( H(L,1,L,2,L), 3, H(L,4,L,5,L), 6, W(L,7,L))As explained in the handout on 2-3 trees, a 2-3 tree is only valid it it satisfies two additional properties:
- The ordering property:
- In a 2-node with left subtree l, value X, and right subtree r, (all values in l) ≤ X ≤ (all values in r).
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, (all values in l) ≤ X ≤ (all values in m) ≤ Y ≤ (all values in r).
- The height property (called path length invariant in the handout): in a 2-node or 3-node, the height of all subtrees must be exactly the same.
The height property guarantees that a valid 2-3 tree is balanced. Together, these two properties guarantee that a 2-3 tree is efficiently searchable.
The file TTTree.sml contains the TTTree dataytype defined above as well as numerous examples of valid and invalid 2-3 trees that are instances of this datatype. Note that t and vt are used for valid trees, io is used for invalidly ordered trees, and ih is used for invalid height trees.
| tree name | elements | ordered? | satisfies the height property? |
|---|---|---|---|
| t1 | [1,…,7] | Yes | Yes, with height 3 |
| t2 | [1,…,7] | Yes | Yes, with height 2 |
| t3 | [1,…,7] | Yes | Yes, with height 2 |
| t4 | [1,…,7] | Yes | Yes, with height 2 |
| vt0 | [] | Yes | Yes, with height 0 |
| vt2 | [1,2] | Yes | Yes, with height 1 |
| vt17 | [1,…,17] | Yes | Yes, with height 3 |
| vt20 | [1,…,20] | Yes | Yes, with height 4 |
| vt44 | [1,…,44] | Yes | Yes, with height 5 |
| vt92 | [1,…,92] | Yes | Yes, with height 6 |
| io2 | [1,2] | No | Yes, with height 1 |
| io7 | [1,…,7] | No | Yes, with height 2 |
| io17 | [1,…,17] | No | Yes, with height 3 |
| io20 | [1,…,20] | No | Yes, with height 4 |
| io44 | [1,…,44] | No | Yes, with height 5 |
| io92 | [1,…,92] | No | Yes, with height 6 |
| ih2 | [1,2] | Yes | No |
| ih7 | [1,…,7] | Yes | No |
| ih17 | [1,…,17] | Yes | No |
| ih20 | [1,…,20] | Yes | No |
| ih44 | [1,…,44] | Yes | No |
| ih92 | [1,…,92] | Yes | No |
These trees are used to define two lists:
val validTrees = [vt0, vt2, t2, t3, t4, t1, vt17, vt20, vt44, vt92]
val invalidTrees = [io2, io7, io17, io20, io44, io92,
ih2, ih9, ih17, ih20, ih44, ih92]In this problem you will (1) implement a validity test for 2-3 trees and (2) implement the effcient 2-3 insertion algorithm from the handout on 2-3 trees.
Begin by copying the starter file TTTreeFuns.sml and flesh out the missing definitions as specified below. (At the end you can rename it to yourAccountName-TTTreeFuns.sml, but there’s no need to do that yet.)
-
satisfiesOrderingProperty(7 points)In this part, you will implement a function
satisfiesOrderingProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree ordering property andfalseif it does not. An easy way to do this is to define two helper functions:elts: TTTree -> int listreturns a list of all the elements of the tree in in-order — i.e.,- In a 2-node with left subtree l, value X, and right subtree r, all values in l are listed before X, which is listed before all elements in r.
- In a 3-node with left subtree l, left value X, middle subtree l, right value Y, and right subtree r, all values in l are listed before X, which is listed before all values in m, which are listed before Y , which is listed before all values in r.
isSorted: int list -> boolreturnstrueif the list of integers is in sorted order andfalseotherwise.
For example:
- elts vt17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] : int list - elts io17; val it = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,17,16] : int list - isSorted(elts vt17); val it = true : bool - isSorted(elts io17); val it = false : boolUsing these two helper functions,
satisfiesOrderingPropertycan be implemented as:fun satisfiesOrderingProperty t = isSorted(elts t)For example:
- map satisfiesOrderingProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesOrderingProperty invalidTrees; val it = [false,false,false,false,false,false,true,true,true,true,true,true] : bool listNotes:
-
Once (and only once) execute
use "TTTree.sml";to load the
TTTreedatatype and example trees. Then every time you change the fileTTTreeFuns.sml, executeuse "TTTreeFuns.sml" -
If you haven’t done so already, read these notes on SML/NJ and Emacs SML Mode and follow the advice there. In particular, it is strongly recommended that you create an SML interpreter within a
*sml*buffer in Emacs. Then you can useM-pandM-nto avoid retyping your test expressions. -
You may need to execute
Control.Print.printLength := 100;in order to see all the list elements. -
Implement
isSortedusing the same zipping approach you used in PS3. You do zipping in SML viaListPair.zipfrom the ListPair module.List.allfrom the List module is also helpful.
-
satisfiesHeightProperty(6 points)In this part, you will implement a function
satisfiesHeightProperty: TTTree -> boolthat takes an instance of theTTTreedatatype and returnstrueif it satisfies the 2-3 tree height property andfalseif it does not. An easy way to do this is to definesatisfiesHeightPropertyasfun satisfiesHeightProperty t = Option.isSome (height t)where
Option.isSomeis a function from the Option module that determines if anoptionvalue is aSOME(vs. aNONE) andheightis a function with typeTTTree -> option intsuch thatheight treturnsSOME hiftsatisfies the height property with heighthand otherwise returnsNONE.Implement the
heightfunction by fleshing out this skeleton:(* height: TTTree -> int option *) fun height L = (* return an appropriate option value here *) | height (W(l, _, r)) = (case (height(l), height(r)) of (* put appropriate pattern clauses here *)) | (* handle the H case here, similarly to the W case *)For example:
- map height validTrees; val it = [SOME 0,SOME 1,SOME 2,SOME 2,SOME 2,SOME 3,SOME 3,SOME 4,SOME 5,SOME 6] : int option list - map height invalidTrees; val it = [SOME 1,SOME 2,SOME 3,SOME 4,SOME 5,SOME 6,NONE,NONE,NONE,NONE,NONE,NONE] : int option listNotes:
-
It’s important to enclose the
caseexpressions withinheightin parens to distinguish the pattern clauses of thecaseexpression from those of theheightfunction definition. -
Once
heightis defined,satisfiesHeightPropertyis defined:- map satisfiesHeightProperty validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map satisfiesHeightProperty invalidTrees; val it = [true,true,true,true,true,true, false,false,false,false,false,false] : bool list -
Once both
satisfiesOrderingPropertyandsatisfiesHeightPropertyare defined, it is trivial to define a functionisValid: TTTree -> boolthat returnstrueif a given 2-3 tree is valid andfalseotherwise.fun isValid t = satisfiesOrderingProperty t andalso satisfiesHeightProperty t - map isValid validTrees; val it = [true,true,true,true,true,true,true,true,true,true] : bool list - map isValid invalidTrees; val it = [false,false,false,false,false,false, false,false,false,false,false,false] : bool list
-
-
insert(12 points) In this part, you will implement the insertion algorithm for 2-3 trees as described on pages 3 to 5 of the handout on 2-3 trees. You will not implement the special cases described on page 6 .The insertion algorithm is a recursive algorithm that uses the notion of a pseudo 2-node that is “kicked up” in certain cases and handled specially in the upward phase of the recursion. To distinguish an insertion result that is a regular 2-3 tree from a pseudo 2-node that is “kicked up”, we use the following datatype:
datatype InsResult = Tree of TTTree | KickedUp of TTTree * int * TTTree (* pseudo 2-node "kicked up" from below *)You will implement 2-3 tree insertion via a pair of functions:
-
(insert v t)returns the newTTTreethat results from inserting a given intvinto a given treet.inserthas typeint -> TTTree -> TTTree. -
(ins v t)is a helper function that returns the instance ofInsResultthat results from inserting a given intvinto a given treet.inshas typeint -> TTTree -> InsResult.
Your implementation should flesh out the following code skeleton by turning the pictures on pages 3 to 5 from the handout on 2-3 trees into SML code.
(* insert: int -> TTTree -> TTTree *) fun insert v t = case ins v t of Tree t => t | KickedUp(l, w, r) => W(l, w, r) and (* "and" glues together mutually recursive functions *) (* ins: int -> TTTree -> InsResult *) ins v L = KickedUp (L, v, L) | ins v (W(l, X, r)) = if v <= X then (case ins v l of Tree l' => Tree(W(l', X, r)) | KickedUp (l', w, m) => Tree(H(l', w, m, X, r))) else (* flesh this out *) | (* handle an H node similarly to the W node based on rules from the handout *)Notes:
-
The
insfunction should only callinsrecursively and should not callinsert. -
An easy way to test
insertis to call the followinglistToTTTreefunction on a list of numbers generated byrange. (These are already defined in your starter file.) Note that you may need to increase the print depth (viaControl.Print.printDepth := 100) in order to see all the details of the printed trees:fun listToTTTree xs = foldl (fn (x,t) => insert x t) L xs fun range lo hi = if lo >= hi then [] else lo :: (range (lo + 1) hi) - listToTTTree (range 1 8); val it = W (W (W #,2,W #),4,W (W #,6,W #)) : TTTree - listToTTTree (range 1 17); val it = W (W (W #,4,W #),8,W (W #,12,W #)) : TTTree - Control.Print.printDepth := 100; val it = () : unit - listToTTTree (range 1 7); val it = H (W (L,1,L),2,W (L,3,L),4,H (L,5,L,6,L)) : TTTree - listToTTTree (range 1 18); val it = W (W (W (W (L,1,L),2,W (L,3,L)),4,W (W (L,5,L),6,W (L,7,L))),8, W (W (W (L,9,L),10,W (L,11,L)),12, H (W (L,13,L),14,W (L,15,L),16,W (L,17,L)))) : TTTree - listToTTTree (range 1 45); val it = W (W (W (W (W (L,1,L),2,W (L,3,L)),4,W (W (L,5,L),6,W (L,7,L))),8, W (W (W (L,9,L),10,W (L,11,L)),12,W (W (L,13,L),14,W (L,15,L)))),16, H (W (W (W (L,17,L),18,W (L,19,L)),20,W (W (L,21,L),22,W (L,23,L))),24, W (W (W (L,25,L),26,W (L,27,L)),28,W (W (L,29,L),30,W (L,31,L))),32, H (W (W (L,33,L),34,W (L,35,L)),36,W (W (L,37,L),38,W (L,39,L)),40, W (W (L,41,L),42,H (L,43,L,44,L))))) : TTTree -
Unfortunately, inserting elements in sequential order as above tends to create 2-3 trees with almost all 2-nodes and very few 3-nodes. It turns out a better way is to mix up the order of insertion as is done in the following code for
makeTTTree. This results in trees that have a good mix of 2-nodes and 3-nodes:(* Return list that has all ints in nums, but those not divisible by 3 come before those divisible by three *) fun arrangeMod3 nums = let val (zeroMod3, notZeroMod3) = List.partition (fn n => (n mod 3) = 0) nums in notZeroMod3 @ zeroMod3 end (* Make a 2-3 tree with elements from 1 up to and including size. Use arrangeMod3 to mix up numbers and lead to more 3-nodes than we'd get with sorted integers lists *) fun makeTTTree size = listToTTTree (arrangeMod3 (range 1 (size + 1))) - makeTTTree 17; val it = H (W (W (L,1,L),2,H (L,3,L,4,L)),5,W (H (L,6,L,7,L),8,H (L,9,L,10,L)),11, H (H (L,12,L,13,L),14,W (L,15,L),16,W (L,17,L))) : TTTree - makeTTTree 44; val it = W (W (W (W (W (L,1,L),2,H (L,3,L,4,L)),5,W (H (L,6,L,7,L),8,H (L,9,L,10,L))), 11, W (W (H (L,12,L,13,L),14,H (L,15,L,16,L)),17, W (H (L,18,L,19,L),20,H (L,21,L,22,L)))),23, W (W (W (H (L,24,L,25,L),26,H (L,27,L,28,L)),29, W (H (L,30,L,31,L),32,H (L,33,L,34,L))),35, W (W (H (L,36,L,37,L),38,H (L,39,L,40,L)),41, W (W (L,42,L),43,W (L,44,L))))) : TTTree -
Finally, to test your insertion implementation more extensively, try
(testInsert 1000)with the following function, which will usemakeTTTreeto create 2-3 trees containing 0 elements to 1000 elements and warn you of any invalid trees.fun testInsert upToSize = let val pairs = map (fn n => (n, makeTTTree n)) (range 0 (upToSize + 1)) val (validPairs, invalidPairs) = List.partition (fn (_,t) => isValid t) pairs val wrongElts = List.filter (fn (n,t) => (elts t) <> (range 1 (n + 1))) validPairs in if (null invalidPairs) andalso (null wrongElts) then (print "Passed all test cases\n"; []) else if (not (null invalidPairs)) then (print "There are invalid trees in the following cases\n"; invalidPairs) else (print "The elements or element order is wrong in the following cases\n"; wrongElts) end - testInsert 1000; Passed all test cases val it = [] : (int * TTTree) list -
When you are done with this problem, rename
TTTreeFuns.smltoyourAccountName-TTTreeFuns.smlbefore submitting your work.
-
Extra Credit: PostFix Iterations (15 points)
-
(5 points) Study and test the following
mysteryPostFix program of one argument, which is provided near the end of the file. Describe the function that it calculates on its one argument, and give a brief, high-level description of how it calculates that function.;; What function does this compute? (define mystery '(postfix 1 1 (swap dup 0 eq (swap) (swap 2 nget mul swap 1 sub swap 3 nget exec) sel exec) 3 rot 3 nget exec)) -
(10 points) Write a PostFix program that takes a single argument (assumed to be a nonnegative integer n) and iteratively calculates the nth Fibonacci number.
Extra Credit: 2-3 Tree Deletion (20 points)
In SML, implement and test the 2-3 tree deletion algorithm presented in pages 8 through 11 of the handout on 2-3 trees.
Extra Credit: 2-3 Trees in Java (35 points)
Implement and test 2-3 tree insertion and deletion in Java. Compare the SML and Java implementations. Which features of which languages make the implementation easier and why?