CS 251: PS6: Practicing PostFix and Starting SML

Due: Wednesday, Nov 16. This extended deadline is a realistic one everyone should try to meet.
Notes:
- This pset contains two solo problems worth 30 points.
- This pset has 100 total points.
- The problems needn’t be done in order. Feel free to jump around.
Submission:
- In your yourFullName CS251 Fall 2016 Folder, create a Google Doc named yourFullName CS251 PS6.
- At the top of your yourFullName CS251 PS6 doc, include your name, problem set number, date of submission, and an approximation of how long each problem part took.
- For all parts of all problems, include all answers (including Racket and SML code) in your PS6 google doc. Format Racket and SML code using a fixed-width font, like Consolas or Courier New. You can use a small font size if that helps.
- For Problems 1 and 2 (the solo problems)
  - Include the English answers to parts 1a, 1b, and 2a in your PS6 google doc.
  - Be sure that all function definitions in yourAccountName-ps6-solo.rkt also appear in your Google Doc (so that I can comment on them)
  - Drop a copy of your yourAccountName-ps6-solo.rkt in your ~/cs251/drop/ps06 drop folder on cs.wellesley.edu.
- For Problem 3:
  - Be sure that your deep-reverse definition in yourAccountName-ps6-deep-reverse.rkt also appears in your Google Doc.
  - Drop a copy of your yourAccountName-ps6-deep-reverse.rkt in your ~/cs251/drop/ps06 drop folder on cs.wellesley.edu.
- For Problem 4:
  - Include the modified parts of yourAccountName-ps6-postfix.rkt in your Google Doc. (You only need to include the modified parts, not the entire contents of the PostFix interpreter!)
  - Drop a copy of your yourAccountName-ps6-postfix.rkt in your ~/cs251/drop/ps06 drop folder on cs.wellesley.edu.
- For Problem 5:
  - Include the SML code from yourAccountName-ps6.sml in your Google Doc.
  - Drop a copy of your yourAccountName-ps6.sml in your ~/cs251/drop/ps06 drop folder on cs.wellesley.edu.

1. Solo Problem: Partial Reverses (20 points)

This is a solo problem. This means you must complete it entirely on your own without help from any other person and without consulting resources other than course materials or online documentation. You may ask Lyn for clarification, but not for help.

Begin this problem by downloading this starter file ps6-solo-starter.rkt, which you should rename to yourAccountName-ps6-solo.rkt. This file contains provided definitions for both Problems 1 and 2. Add your definitions for Problems 1 and 2 to this file.

(5 points) Consider the following partial-reverses function. Draw a box-and-pointer diagram of the list that results from the invocation (partial-reverses '(1 2 3 4)). Use the style of diagram shown in PS3 Problem 2. Study the code carefully and be sure to accurately show all sharing between cons celsls in your diagram.
```
(define (partial-reverses xs)
  (partial-reverses-tail xs '() '()))

(define (partial-reverses-tail ys rev list-rev)
  (if (null? ys)
      (cons rev list-rev)
      (partial-reverses-tail (rest ys)
                             (cons (first ys) rev)
                             (cons rev list-rev)
                             )))
```
Note: As an example of sharing in box-and-pointer diagrams, consider
```
(define numList '(7 2 4))

(define listOfNumLists (list (append numList (rest numList)) numList (rest numList)))
```
(Note: an earlier version of this pset had several occurrences of the incorrect nums instead of the correct numList)

The result has 9 cons cells arranged as follows:

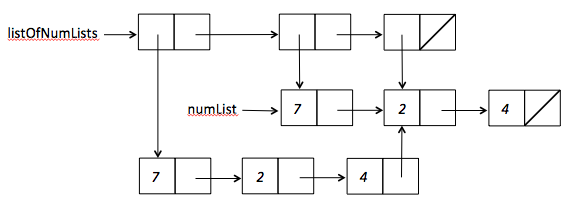
However, if we just enter the printed representation '((7 2 4 2 4) (7 2 4) (2 4)) for listOfNumLists, that would create 13 cons cells: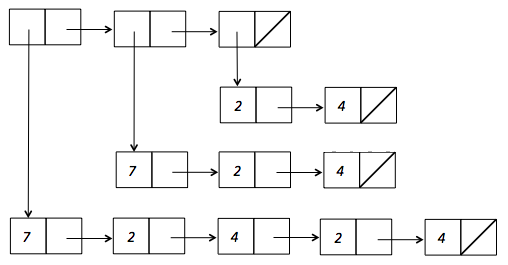
(1 points) How many cons cells would there be in the result of (partial-reverses-iter range (1 1001))?

(7 points) Complete the following definition of partial-reverses-iterate so that it uses iterate-apply to iteratively calculte the same result (including sharing) as partial-reverses:

(define (partial-reverses-iterate xs)
  (iterate-apply ; expression1 
                 ; expression2
                 ; expression3
                 ; expression4
                 ))

In your expressions, the only functions you may use are list, cons, first, rest, null, and null?.

Recall that iterate-apply is defined as follows:

(define (iterate-apply next done? finalize state)
  (if (apply done? state)
      (apply finalize state)
      (iterate-apply next done? finalize (apply next state))))

(7 Points) Complete the following definition of partial-reverses-foldl so that it uses foldl to iteratively calculte the same result (including sharing) as partial-reverses:
```
(define (partial-reverses-foldl xs)
  (foldl ; expression1
         ; expression2
         xs))
```
In your expressions, the only functions you may use are list, cons, first, and null.

2. Solo Problem: Weighted Sums (10 points)

For this problem, use the same yourAccountName-ps6-solo.rkt file you created for Problem 1.

(4 points) Consider the following weighted-sums function. Carefully describe in English the output list that is returned when weighted-sums is called on a list of n numbers. How many elements are in the output list? What is the ith element of the output list as a function of the elements of the input list? What does the function return for an empty list? A singleton list?

(define (weighted-sums numbers)
  (map (λ (nums) (* (first nums) (foldl + 0 (rest nums))))
       (genlist rest null? #f numbers)))

(define (genlist next done? keepLastValue? seed)
  (if (done? seed)
      (if keepLastValue? (list seed) null)
      (cons seed (genlist next done? keepLastValue? (next seed)))))

(6 points) Below is the skeleton of a weighted-sums-iter function that uses tail recursion to iteratively calculate via nested loops the same result as weighted-sums. Flesh out the 8 missing expressions delimited by angle brackets so that it works correctly. The only functions you may use in your answer are cons, first, rest, null, +, and *.

(define (weighted-sums-iter numbers)
  (define (outer-tail sums nums)
    (define (inner-tail sum ns)
      (if (null? ns)
          (outer-tail <sumsVal2> <numsVal2>)
          (inner-tail <sumVal2> <nsVal2>)))
    (if (null? nums)
        (reverse sums)
        (inner-tail <sumVal1> <nsVal1>)))
  (outer-tail <sumsVal1> <numsVal1>))

3. Deep Reverse (10 points)

We saw in lecture that tree recursion on trees represented as s-expressions could be expressed rather elegantly. For example:

(define (atom? x)
  (or (number? x) (boolean? x) (string? x) (symbol? x)))

(define (num-atoms sexp)
  (if (atom? sexp)
      1
      (foldr + 0 (map num-atoms sexp))))

> (num-atoms '((a (b c) d) e (((f) g h) i j k)))
11
> (num-atoms '(a b c d))
4
> (num-atoms 'a)
1
> (num-atoms '())
0

(define (atoms sexp)
  (if (atom? sexp)
      (list sexp)
      (foldr append null (map atoms sexp))))

> (atoms '((a (b c) d) e (((f) g h) i j k)))
'(a b c d e f g h i j k)
> (atoms '(a b c d))
'(a b c d)
> (atoms 'a)
'(a)
> (atoms '())
'()

In this problem, you will define a function (deep-reverse sexp) that returns a new s-expression in which the order of the children at every node of the s-expression tree sexp is reversed.

> (deep-reverse '((a (b c) d) e (((f) g h) i j k)))
'((k j i (h g (f))) e (d (c b) a))
> (deep-reverse '(a b c d))
'(d c b a)
> (deep-reverse 'a)
'a
> (deep-reverse '())
'()

Notes:

Begin with this starter file ps6-deep-reverse-starter.rkt, which you should rename to yourAccountName-ps6-deep-reverse.rkt. Add your definition of deep-reverse to this file.
Your definition should have form similar to the defintions for num-atoms and atoms, but you’ll want to use something other than foldr.

4. Extending PostFix (30 points)

fIn lecture we studied several different versions of an interpreter for the PostFix language implemented in Racket. This pset involves starting with the following version of the interpreter:

ps6-postfix-starter.rkt

This is a slightly modified version of the file postfix-transform-fancy.rkt studied in lecture.

Begin by making a copy of ps6-postfix-starter.rkt named yourAccountName-ps6-postfix.rkt and load this into Dr. Racket. Near the bottom of this file is the following PostFix program named sos (for “sum of squares”). Racket’s semi-colon comments have been used to explain the commands in the program:

;; Sum-of-squares program 
(define sos
  '(postfix 2 ; let's call the arguments a and b, from top down
            1 nget ; duplicate a at top of stack
            mul ; square a
            swap ; stack now has b and a^2 from top down
            1 nget mul ; square b
            add ; add b^2 + a^2 and return
            ))

Let’s run the program on the arguments 5 and 12:

> (postfix-run sos '(5 12))
About to execute commands (1 nget mul swap 1 nget mul add) on stack (5 12)
  after executing 1, stack is (1 5 12)
  after executing nget, stack is (5 5 12)
  after executing mul, stack is (25 12)
  after executing swap, stack is (12 25)
  after executing 1, stack is (1 12 25)
  after executing nget, stack is (12 12 25)
  after executing mul, stack is (144 25)
  after executing add, stack is (169)
169

Note that the stack that results from executing each command on the previous stack is displayed, line by line. This behavior is controlled by the print-stacks? flag at the top of the program:

(define print-stacks? #t)

If we set the flag to #f, the intermediate stack display will be turned off:

(define print-stacks? #f)

> (postfix-run sos '(5 12))
169

Turn the print-stacks? flag on when it’s helpful to understand or debug a PostFix program.

(10 points)

Consider the following Racket function g that is defined near the bottom of the PostFix intepreter file:

(define (g a b c)
  (- c
     (if (= 0 (remainder a 2))
         (quotient b (- a c))
         (* (+ b c) a))))

(Note: an earlier version of ps6-postfix-starter.rkt had an incorrect definition of the function g. If you have the earlier version of the starter .rkt file, replace the definition of g in that file by the one above.)

In this part, your goal is to flesh out the definition of a three-argument PostFix program pfg that performs the same calculation as g on three arguments:

(define pfg
   '(postfix 3 
       ;; Flesh out and comment the commands in this PostFix program 
     ))

Here are some examples with a correctly defined pfg:

> (apply g '(10 2 8))
7

> (postfix-run pfg '(10 2 8))
7

> (apply g '(-7 2 3))
38

> (postfix-run pfg '(-7 2 3))
38

> (apply g '(5 4 5))
-40

> (postfix-run pfg '(5 4 5))
-40

Notes:

*An earlier version of this pset had the answer 3 for running g and pfg on '(10 2 8), but the result should be 7.

Please comment the commands in pfg like those in sos.

You have been provided with a testing function (test-pfg) that will test your pfg function on 5 sets of arguments:

;; Tests on an incorrect definition of pfg: 
> (test-pfg)
Testing pfg on (10 2 8): ***different results***
  g: 3
  pfg: -3
Testing pfg on (11 2 8): ***different results***
  g: -102
  pfg: 102
Testing pfg on (-6 3 8): ***different results***
  g: 10
  pfg: -10
Testing pfg on (-7 2 3): ***different results***
  g: 38
  pfg: -38
Testing pfg on (5 4 5): ***different results***
  g: -40
  pfg: -40

;; Tests on a correct definition of pfg: 
> (test-pfg)
Testing pfg on (10 2 8):  same result for g and pfg = 3
Testing pfg on (11 2 8):  same result for g and pfg = -102
Testing pfg on (-6 3 8):  same result for g and pfg = 10
Testing pfg on (-7 2 3):  same result for g and pfg = 38
Testing pfg on (5 4 5):  same result for g and pfg = -40

(5 points) Extend PostFix by adding the following three commands:

le is like lt, but checks “less than or equal to” rather than “less than”
ge is like gt, but checks “greater than or equal to” rather than “greater than”
and expects two integers at the top of the stack. It replaces them by 0 if either is 0; otherwise it replaces them by 1.

For example:

> (postfix-run '(postfix 0 4 5 le) '())
1

> (postfix-run '(postfix 0 5 5 le) '())
1

> (postfix-run '(postfix 0 5 4 le) '())
0

> (postfix-run '(postfix 0 4 5 ge) '())
0

> (postfix-run '(postfix 0 4 4 ge) '())
1

> (postfix-run '(postfix 0 5 4 ge) '())
1

> (postfix-run '(postfix 0 0 0 and) '())
0

> (postfix-run '(postfix 0 0 1 and) '())
0

> (postfix-run '(postfix 0 1 0 and) '())
0

> (postfix-run '(postfix 0 0 17 and) '())
0
 
> (postfix-run '(postfix 0 17 0 and) '())
0

> (postfix-run '(postfix 0 1 1 and) '())
1

> (postfix-run '(postfix 0 1 17 and) '())
1

> (postfix-run '(postfix 0 17 17 and) '())
1
 
> (postfix-run '(postfix 0 17 23 and) '())
1

Notes:

Do not modify postfix-exec-command for this part. Instead, just add three bindings to the list postfix-relops.

The testing function (test-3b) will test all of le, ge, and and in the context of the single PostFix program test-sorted:

(define test-sorted '(postfix 3 ; let's call the arguments a, b, and c, from top down
                         2 nget le ; is a <= b?
                         3 nget 3 nget ge ; is c >= b?
                         and ; is a <= b and c >= b?
                         ))

> (test-3b) ; Uses the test-sorted program in its definition 
Trying test-sorted on (4 5 6): works as expected; result = 1
Trying test-sorted on (4 5 5): works as expected; result = 1
Trying test-sorted on (4 4 5): works as expected; result = 1
Trying test-sorted on (4 4 4): works as expected; result = 1
Trying test-sorted on (4 6 5): works as expected; result = 0
Trying test-sorted on (5 6 4): works as expected; result = 0
Trying test-sorted on (5 4 6): works as expected; result = 0
Trying test-sorted on (6 5 4): works as expected; result = 0
Trying test-sorted on (6 4 5): works as expected; result = 0
Trying test-sorted on (5 5 4): works as expected; result = 0
Trying test-sorted on (5 4 4): works as expected; result = 0

(5 points) Extend PostFix with a dup command that duplicates the top element of the stack (which can be either an integer or executable sequence). For example:

(define sos-dup '(postfix 2 dup mul swap dup mul add))

> (postfix-run sos-dup '(3 4))
About to execute commands (dup mul swap dup mul add) on stack (3 4)
  after executing dup, stack is (3 3 4)
  after executing mul, stack is (9 4)
  after executing swap, stack is (4 9)
  after executing dup, stack is (4 4 9)
  after executing mul, stack is (16 9)
  after executing add, stack is (25)
25

(define cmd-dup '(postfix 1 (dup dup mul add swap) dup 3 nget swap exec exec pop))

> (postfix-run cmd-dup '(4))
About to execute commands ((dup dup mul add swap) dup 3 nget swap exec exec pop) on stack (4)
  after executing (dup dup mul add swap), stack is ((dup dup mul add swap) 4)
  after executing dup, stack is ((dup dup mul add swap) (dup dup mul add swap) 4)
  after executing 3, stack is (3 (dup dup mul add swap) (dup dup mul add swap) 4)
  after executing nget, stack is (4 (dup dup mul add swap) (dup dup mul add swap) 4)
  after executing swap, stack is ((dup dup mul add swap) 4 (dup dup mul add swap) 4)
About to execute commands (dup dup mul add swap) on stack (4 (dup dup mul add swap) 4)
  after executing dup, stack is (4 4 (dup dup mul add swap) 4)
  after executing dup, stack is (4 4 4 (dup dup mul add swap) 4)
  after executing mul, stack is (16 4 (dup dup mul add swap) 4)
  after executing add, stack is (20 (dup dup mul add swap) 4)
  after executing swap, stack is ((dup dup mul add swap) 20 4)
  after executing exec, stack is ((dup dup mul add swap) 20 4)
About to execute commands (dup dup mul add swap) on stack (20 4)
  after executing dup, stack is (20 20 4)
  after executing dup, stack is (20 20 20 4)
  after executing mul, stack is (400 20 4)
  after executing add, stack is (420 4)
  after executing swap, stack is (4 420)
  after executing exec, stack is (4 420)
  after executing pop, stack is (420)
420

> (postfix-run '(postfix 0 dup) '())
ERROR: dup requires a nonempty stack ()

Notes:

Implement dup by adding a cond clause to postfix-exec-command.
Test your dup implementation using the above test cases. Your dup implementation should ensure there is at least one value on the stack, and give an appropriate error message when there isn’t.

(10 points) In this part you will extend PostFix with a rot command that behaves as follows. The top stack value should be a positive integer rotlen that we’ll call the rotation length. Assume there are n values v₁, …, v_n below rotlen on the stack, where n is greater than or equal to rotlen. Then the result of performing the rot command is to rotate the top rotlen elements of the stack by moving v₁ after v_rotlen. I.e., the order of values on the stack after rot should be v₂, …, v_rotlen, v₁, v_rotlen+1, …, v_n. So the first rotlen elements of the stack have been rotated by one unit, while the order of the remaining elements on the stack is unchanged.

Here are examples involving rot:

(define rot-test '(postfix 6 4 rot 3 rot 2 rot))

> (postfix-run rot-test '(8 7 6 5 9 10))
About to execute commands (4 rot 3 rot 2 rot) on stack (8 7 6 5 9 10)
  after executing 4, stack is (4 8 7 6 5 9 10)
  after executing rot, stack is (7 6 5 8 9 10)
  after executing 3, stack is (3 7 6 5 8 9 10)
  after executing rot, stack is (6 5 7 8 9 10)
  after executing 2, stack is (2 6 5 7 8 9 10)
  after executing rot, stack is (5 6 7 8 9 10)
5

> (postfix-run '(postfix 3 (mul add) rot) '(5 6 7))
About to execute commands ((mul add) rot) on stack (5 6 7)
  after executing (mul add), stack is ((mul add) 5 6 7)
ERROR: rot length must be a positive integer but is (mul add)

> (postfix-run '(postfix 3 -1 rot) '(5 6 7))
About to execute commands (-1 rot) on stack (5 6 7)
  after executing -1, stack is (-1 5 6 7)
ERROR: rot length must be a positive integer but is -1

> (postfix-run '(postfix 3 4 rot) '(5 6 7))
About to execute commands (4 rot) on stack (5 6 7)
  after executing 4, stack is (4 5 6 7)
ERROR: not enough stack values for rot (4 5 6 7)

> (postfix-run '(postfix 0 rot) '())
About to execute commands (rot) on stack ()
ERROR: rot requires a nonempty stack but is ()

Notes:

Implement rot by adding a cond clause to postfix-exec-command.

Racket supplies a list-tail function that is very helpful for implementing rot:

> (list-tail '(10 20 30 40 50) 0)
'(10 20 30 40 50)

> (list-tail '(10 20 30 40 50) 1)
'(20 30 40 50)

> (list-tail '(10 20 30 40 50) 2)
'(30 40 50)

> (list-tail '(10 20 30 40 50) 3)
'(40 50)

> (list-tail '(10 20 30 40 50) 4)
'(50)

> (list-tail '(10 20 30 40 50) 5)
'()

Racket does not provide a similar list-head function, but I have provided it in the .rkt file. It works this way:

> (list-head '(10 20 30 40 50) 0)
'()

> (list-head '(10 20 30 40 50) 1)
'(10)

> (list-head '(10 20 30 40 50) 2)
'(10 20)

> (list-head '(10 20 30 40 50) 3)
'(10 20 30)

>  (list-head '(10 20 30 40 50) 4)
'(10 20 30 40)

>  (list-head '(10 20 30 40 50) 5)
'(10 20 30 40 50)

Test your rot implementation using the above test cases. Your rot implementation should give appropriate error messages in various situations, like those in the test cases.

5. Higher-order List Operators in SML (30 points)

In this problem, you will revisit many of the higher-order list operators we have studied in Racket in the context of SML. Since you are already familiar with these operators, your focus in this problem is on SML syntax and type-checking, rather than on the operators themselves.

Write all of your SML code in a new file named yourAccountName-ps6.sml.

range, alts, cartesianProduct (14 points) Translate the following Racket range, alts, and cartesian-product functions into SML range, alts, and cartesianProduct functions:

(define (range lo hi)
  (if (<= hi lo)
      null
      (cons lo (range (+ 1 lo) hi))))

(define (alts xs)
  (foldr (λ (x subResult) (list (cons x (second subResult)) (first subresult)))
         (list '() '())
         xs

(define (my-cartesian-product xs ys)
  (foldr (λ (x subres) (append (map (λ (y) (cons x y)) ys)  subres))
         null 
         xs))

For example:

val range = fn : int -> int -> int list
val alts = fn : 'a list -> 'a list * 'a list
val cartesianProduct = fn : 'a list -> 'b list -> ('a * 'b) list

- range 0 10;
val it = [0,1,2,3,4,5,6,7,8,9] : int list

- range 3 8;
val it = [3,4,5,6,7] : int list

- range 5 5;
val it = [] : int list

- range 1 100;
val it = [1,2,3,4,5,6,7,8,9,10,11,12,...] : int list

- Control.Print.printLength := 100;

- val it =
  [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,
   29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,
   54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,
   79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99] : int list

- alts [7, 5, 4, 6, 9, 2, 8, 3];
val it = ([7,4,9,8],[5,6,2,3]) : int list * int list

- alts (range 0 20);
val it = ([0,2,4,6,8,10,12,14,16,18],[1,3,5,7,9,11,13,15,17,19])
  : int list * int list

- cartesianProduct [1,2,3,4] ["a", "b", "c"];
val it =
  [(1,"a"),(1,"b"),(1,"c"),(2,"a"),(2,"b"),(2,"c"),(3,"a"),(3,"b"),(3,"c"),
   (4,"a"),(4,"b"),(4,"c")] : (int * string) list

- cartesianProduct ["a", "b", "c"] [1,2,3,4];
val it =
  [("a",1),("a",2),("a",3),("a",4),("b",1),("b",2),("b",3),("b",4),("c",1),
   ("c",2),("c",3),("c",4)] : (string * int) list

Notes:

If you haven’t done so already, read these notes on SML/NJ and Emacs SML Mode and follow the advice there. In particular, it is strongly recommended that you create an SML interpreter within a *sml* buffer in Emacs. Then you can use M-p and M-n to avoid retyping your test expressions.
Because hyphens are not allowed in SML identifiers, you should translate all hyphens in Racket identifiers either to underscores or camel case. E.g., cartesian-product in Racket becomes cartesian_product or cartesianPrduct in SML.
Be careful with your explicit parentheses in SML. Many type errors in SML programs come from incorrectly parenthesizing expressions.

foldr, map are both built into SML:

val foldr = fn: ('a * 'b -> 'b) -> 'b -> 'a list -> 'b
val map = fn: ('a -> 'b) -> 'a list -> 'b list

Racket’s append translates to SML’s infix @ operator, but when you want to pass it as an argument to a first-class function you write it as op@.
In this entire problem (not just this part) some instances of Racket’s cons will translate to SML’s infix list-prepending operator ::, while others will translate to the tupling notation (<exp1>, <exp2>) for pair creation. Reason about SML types to figure out which to use when. SML’s type checker will yell at you if you get it wrong.
In this entire problem (not just this part) some instances of Racket’s list will translate to SML’s lists while others will translate to SML’s tuples. Again, reason about SML types to figure out which to use when.

Control.Print.printLength controls how many list elements are displayed; after this number, ellipses are used. For example:

- Control.Print.printLength := 5;
val it = () : unit

- range 0 20;
val it = [0,1,2,3,4,...] : int list

- Control.Print.printLength := 20;
val it = () : unit

- range 0 20;
val it = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19] : int list

Another such control is Control.Print.printDepth, which controls printing in nested lists. You won’t need that here, but might in the future.

allContainMultiple and isSorted (8 points) Translate the following Racket all-contain-multiple? and sorted? functions into SML doAllContainMultple and isSorted functions:

(define (all-contain-multiple? m nss)
  (forall? (lambda (ns)
             (exists? (lambda (n) (divisible-by? n m))
                      ns))
            nss))

(define (sorted? ns)
  (if (null ns)
      #t ; special case to avoid (rest ns) below
      (forall? (λ (pair) (<= (car pair) (cdr pair)))
               (zip ns (rest ns)))))

For example:

- allContainMultiple 5 [[17,10,2],[25],[3,8,5]];
val it = true : bool

- allContainMultiple 2 [[17,10,2],[25],[3,8,5]];
val it = false : bool

- allContainMultiple 3 [];
val it = true : bool

- isSorted [7,4,2,5,4,6];
val it = false : bool

- isSorted [2,3,3,5,6,7];
val it = true : bool

- isSorted [2];
val it = true : bool

- isSorted [];
val it = true : bool

- isSorted (range 0 1000);
val it = true : bool

- isSorted ((range 0 1000) @ [1001,1000]);
val it = false : bool

Notes:

SML includes the following analogs of forall?, exists?, and zip that you should use in your definitions:

- List.all;
val it = fn : ('a -> bool) -> 'a list -> bool

- List.exists;
val it = fn : ('a -> bool) -> 'a list -> bool

- ListPair.zip;
val it = fn : 'a list * 'b list -> ('a * 'b) list

Because SML does not allow ? in identifiers, Racket names containing ? need to be be transformed, as in sorted? to isSorted
The List. and ListPair. indicate that these functions come from modules. Here is documentation on the List module, and here is documentation on the ListPair module.

genlist (8 points) Translate the following Racket genlist and partial-sums-table functions into SML genlist and partialSumsTable functions:

(define (genlist next done? keepDoneValue? seed)
  (if (done? seed)
      (if keepDoneValue? (list seed) null)
      (cons seed (genlist next done? keepDoneValue? (next seed)))))

(define (partial-sums-table ns)
  (genlist (λ (nums&ans)
             (list (rest (first nums&ans)) (+ (first (first nums&ans)) (second nums&ans))))
           (λ (nums&ans) (null? (first nums&ans)))
           #t 
           (list ns 0)))

For example:

val genlist = fn : ('a -> 'a) -> ('a -> bool) -> 'a -> 'a list
val pairs_genlist = fn : int -> (int * int) list

- genlist (fn n => n * 2) (fn n => n > 1000) true 1;
val it = [1,2,4,8,16,32,64,128,256,512,1024] : int list

- genlist (fn n => n * 2) (fn n => n > 1000) false 1;
val it = [1,2,4,8,16,32,64,128,256,512] : int list

- partialSumsTable [7, 2, 5, 8, 4];
val it =
  [([7,2,5,8,4],0),([2,5,8,4],7),([5,8,4],9),([8,4],14),([4],22),([],26)]
  : (int list * int) list

- partialSumsTable (range 1 11);
val it =
  [([1,2,3,4,5,6,7,8,9,10],0),([2,3,4,5,6,7,8,9,10],1),([3,4,5,6,7,8,9,10],3),
   ([4,5,6,7,8,9,10],6),([5,6,7,8,9,10],10),([6,7,8,9,10],15),([7,8,9,10],21),
   ([8,9,10],28),([9,10],36),([10],45),([],55)] : (int list * int) list

Notes:

SML does not allow ? in identifiers, so translate done? to is_done or isDone and similarly with keepDoneValue?
Use pattern matching on tuples when translating the (λ (nums&ans) ...) functions. Translate these to (fn (nums,ans) => ...). Because of SML’s built-in pattern matching, in SML it is unnecessary to have a separate function like Racket’s genlist-apply in SML since the function arguments in SML’s genlist can already do pattern matching.

Extra Credit: PostFix Iterations (30 points)

(5 points) Study and test the following mystery PostFix program of one argument, which is provided near the end of the file. Describe the function that it calculates on its one argument, and give a brief, high-level description of how it calculates that function.
```
;; What function does this compute? 
(define mystery
  '(postfix 1
            1
            (swap dup 0 eq 
              (swap)
              (swap 2 nget mul swap 1 sub swap 3 vget exec)
              sel exec)
            3 rot 3 vget exec))
```
Note: vget is a command that is like nget, except that it can return any value (including an executable sequence), not just an integer. It has been included in your ps6-postfix-starter.rkt file for use in this extra credit problem.
(15 points) Write a PostFix program that takes a single argument (assumed to be a nonnegative integer n) and iteratively calculates the nth Fibonacci number.
(10 points) The mystery program uses new Postfix commands dup, vget, and rot, but it is possible to write a version of mystery named mystery-only-dup that uses only dup but not vget or rot. Define such a function.