Setup

Get your repository with cs251 start lists --solo.

Tasks

1. Conditional Expressions (15 points)

Write responses for this part in the file cond.txt.

We introduced the if expression in Racket. The original definition of Lisp focused instead on a related cond expression, presented by McCarthy in his 1960 paper, Recursive Functions of Symbolic Expressions and Their Computation by Machine, which discussed foundations and implementation details of Lisp. The name cond stands for conditional. Read sections 1-2 (pages 1-8) of McCarthy’s paper to answer the questions below.

Reading Notes

McCarthy uses mathematical notation that differs somewhat from Racket syntax. Here is a conversion from McCarthy’s notation to a syntax that would fit Racket.

(p₁ → e₁, …, p_n → e_n) would be written (cond [p1 e1] ... [pn en]), where all pi and ei are expressions.
T is #t and F is #f.
∧ is boolean and (logical conjunction), ∨ is boolean or (logical disjunction), and ¬ is boolean not (logical negation). (The text defines these standard notations.)
λ((x₁,…,x_n), e) would be (lambda (x1 ... xn) e), where x1 through xn are variable names and e is an expression.

Section 2 gets denser on pages 6-8. The most important material is earlier, but try to pick up what you can from the later parts as well.

Optional Reading

The remainder of McCarthy’s paper is an interesting read as well if you are curious. It describes more features of the Lisp language (still present in Racket) that we will consider briefly later. We will soon return to at least the section describing implementation.

Questions

Where asked for prose answers, please write no more than a few sentences.

Suppose we have support for functions that take a variable number of arguments. As a simple conceptual model, suppose that all argument values are available within the function through a single parameter that is bound to a list of all argument values. For example:
```
; This is made-up syntax -- not real Racket!
(define-varargs (f args)
  ; use `args` as a list of all arguments in body
  body)
```
When evaluating the function application (f 1), args is bound to (list 1). When evaluating the function application (f 1 2 (+ 3 4)), args is bound to (list 1 2 7).

(While the above is not real Racket, Racket does have features that support something similar.)

Suppose we try to implement McCarthy’s conditional as a Racket function cond where all pi and ei are simply passed as arguments. What are some problems with this approach? (Hint, the problems have nothing to do with lists.)
McCarthy describes undefined results for some conditional expressions.

What does it mean for an expression’s result to be undefined? (McCarthy gives an indirect definition of this notion early in Section 2.)
Write two Racket expressions (using only the Racket features we have examined in this course) whose results are undefined, one using recursion and one without.
Write an evaluation rule for cond (using the Racket-style syntax listed above and the style of evaluation rules we have defined in class) to describe the semantics of McCarthy’s conditional expression.
Given the cond syntax shown above and your evaluation rule, we can implement cond as syntactic sugar. Describe in English how to construct an equivalent Racket expression to replace a cond expression. Feel free to show concrete examples of replacement by an equivalent expression, but please describe the general transformation or “desugaring” you would perform given any valid cond expression.

For inspiration, recall how we desugared the short-circuit and operation, (and e1 e2), to the semantically equivalent expression (if e1 e2 #f)) or how we desugared the or expression in class. If you need to produce an undefined result explicitly, call the zero argument function void; it produces “no value.”

2. Concerning Cons Cell Concept Constructs (10 points)

Write answers for this part in the file cons-diagram.rkt.

Consider the following diagram for the list structure named a:

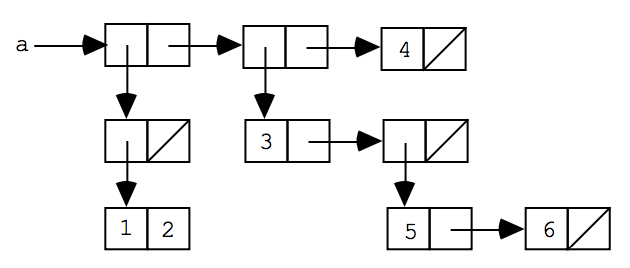
box-and-pointer diagram

Write a Racket definition of the form (define a-cons ____), where ____ is an expression using only cons, null, and the numbers 1 through 6 (but no quote or quotation) to create the structure depicted in the diagram. Do not use list.
Write a Racket definition of the form (define a-list ____), where ____ is an expression using only cons, list, and the numbers 1 through 6 (but no quote or quotation) to create the structure depicted in the diagram. Use list instead of cons and null wherever it is feasible to do so. Use cons only where list cannot be used.
Write a Racket definition of the form (define a-printed ____), where ____ is replaced by the printed representation DrRacket would show if evaluating a in the REPL.
For each of the numbers 1 through 6, write a Racket expression using only car, cdr, and a to extract that number from a. Write the expression in a definition, e.g., (define extract-1 ____), (define extract-2 ____), etc., where ____ is replaced by the expression. You can test these with a-cons or a-list

3. Racket List Programming (75 points)

Write your answers for the following programming problems in the file lists.rkt.

Programming Rules

If at all possible, avoid the use of the built-in list append function (and the equivalent list-append we wrote in lecture today). Some functions below may seem to require append or something equivalent—feel free to use append there, but note its running time is O(n) given an n-element first argument. Soon we will see a new style of recursion for an efficient, elegant alternative.

Update on append

Many folks have been trying very hard to avoid append in all cases. Don’t! With the recursion skills you have available now, you do need it for a few functions. If you are using it for all the functions in this assignment, you’re using it too much, but if you’re using for a few, that’s fine.

Feel free to introduce helper functions where they would be useful in solving the problems (or simplifying the solutions).

Grading Notes

Grading is based on correctness, efficiency, conciseness, elegance, and comments that show you understand how or why your solution works. For example, comments for the list-length function we wrote should be more detailed than, e.g., “list-length returns the length of the given list”, but less detailed than the Racket-to-English translation, “if the argument is null then return zero otherwise return 1 plus the result of a recursive call to list-length on the cdr of the argument.” A good level of detail would be: “list-length returns the length of the given list. An empty list has length zero. A non-empty list has length one greater than the length of the tail (rest) of the list.” There are of course many valid styles of conveying this information, but this should give you an idea of the level of detail to target.

Programming Tasks

Write a function bits that takes a non-negative integer n and returns a list of the bits (0s and 1s) in the binary representation of n.
```
> (bits 5)
'(1 0 1)
> (bits 10)
'(1 0 1 0)
> (bits 11)
'(1 0 1 1)
> (bits 22)
'(1 0 1 1 0)
> (bits 23)
'(1 0 1 1 1)
> (bits 46)
'(1 0 1 1 1 0)
> (bits 1)
'(1)
> (bits 0)
'()
```
Optional 240-tinted challenge: Write a separate function bits-2s that takes a non-negative integer b and an integer n and a returns a list of 0s and 1s representing all digits of the b-bit two’s-complement representation of integer n.
```
> (bits-2s 4 6)
'(0 1 1 0)
> (bits-2s 4 -6)
'(1 0 1 0)
```
Write a function merge that merges two lists into one as in merge-sort. Assuming the two argument lists are each sorted lists of numbers, this function will return a sorted list containing all elements from the two lists. Your function does not need to work for inputs that are not sorted.
```
> (merge (list 1 3 6 7 9 10) (list 2 4 5 8))
'(1 2 3 4 5 6 7 8 9 10)
> (merge (list 4 5 6) (list 1 2 3))
'(1 2 3 4 5 6)
> (merge null null)
'() ; this means null
```

Write a function rev that takes a list xs and reverses its order. You may not use the built-in reverse function.

> (rev (list 1 (list 2 3) (list 4 5 (list 6 7 8))))
'((4 5 (6 7 8)) (2 3) 1)
> (rev (list 1 2 3 4 5))
'(5 4 3 2 1)
> (rev (list 1))
'(1)
> (rev null)
'()

Write a function deep-rev that takes any argument x and deeply reverses it. If x is an atom, deep-rev returns it as is. If x is a cons cell, deep-rev assumes it is a list, reverses the list, and deeply reverse any lists that are elements in x. Assume that cons cells are used only to represent lists. The cons? function returns #t if its argument is a cons cell and #f otherwise.
```
> (deep-rev (list 1 (list 2 3) (list 4 5 (list 6 7 8))))
'(((8 7 6) 5 4) (3 2) 1)
> (deep-rev (list 1 2 3 4 5))
'(5 4 3 2 1)
> (deep-rev (list 1))
'(1)
> (deep-rev null)
'()
```
Write a function contains-multiple that takes an integer m and a list of integers ns that returns #t if m evenly divides at least one element of the integer list ns; otherwise it returns #f. Use modulo to determine divisibility.
```
> (contains-multiple 5 (list 8 10 14))
#t
> (contains-multiple 3 (list 8 10 14))
#f
> (contains-multiple 5 null)
#f
```
Write a function all-contain-multiple that takes an integer n and a list of lists of integers nss (pronounced “enziz”) and returns #t if each list of integers in nss contains at least one integer that is a multiple of n; otherwise it returns #f.
```
> (all-contain-multiple 5 (list (list 17 10 2) (list 25) (list 3 7 5)))
#t
> (all-contain-multiple 3 (list (list 17 10 2) (list 25) (list 3 7 5)))
#f
> (all-contain-multiple 3 null)
#t
```
Assume that the elements of a list are indexed starting with 1. Write a function alts that takes a list of integers xs and returns a pair of lists, the first of which has all the odd-indexed elements (in the same relative order as in xs) and the second of which has all the even-indexed elements (in the same relative order as in xs).
```
> (alts (list 7 5 4 6 9 2 8 3))
'((7 4 9 8) . (5 6 2 3))
> (alts (list 5 4 6 9 2 8 3))
'((5 6 2 3) . (4 9 8))
> (alts (list 4 6 9 2 8 3))
'((4 9 8) . (6 2 3))
> (alts (list 3))
'((3) . ())
> (alts null)
'(() . ())
```
Hint: There is no need to treat even-length and odd-length cases differently, nor is there any need to treat the singleton list specially.
Update on alts

The result notation shown above indicates how to think about the result, but it is not the notation Racket will use to show the result. alts returns a cons cell that represents a pair of two lists: '((4 9 8) . (6 2 3))

Racket displays any cons cell whose cdr is a list as if the top-level cons cell is itself the first cons cell in a list (where the cdr gives the rest of the list): '((4 9 8) 6 2 3)

These are two valid views of the same value.

Since Racket defaults to the latter, it will display the results of a correct implementation like this:
```
> (alts (list 7 5 4 6 9 2 8 3))
'((7 4 9 8) 5 6 2 3)
> (alts (list 5 4 6 9 2 8 3))
'((5 6 2 3) 4 9 8)
> (alts (list 4 6 9 2 8 3))
'((4 9 8) 6 2 3)
> (alts (list 3))
'((3))
> (alts null)
'(())
```
So when we think of the result as '((4 9 8) . (6 2 3)), Racket displays that same value – with different notation – as '((4 9 8) 6 2 3). Not sure? Offer any of the results shown above to the REPL and see what it prints:
```
> '(() . ())
'(())
```

Write a function cartesian-product that takes two lists xs and ys and returns a list of all pairs '(x . y) where x ranges over the elements of xs and y ranges over the elements of ys. The pairs should be sorted first by the x entry (relative to the order in xs) and then by the y entry (relative to the order in ys).

> (cartesian-product (list 1 2) (list "a" "b" "c"))
'((1 . "a") (1 . "b") (1 . "c") (2 . "a") (2 . "b") (2 . "c"))
> (cartesian-product (list 2 1) (list "a" "b" "c"))
'((2 . "a") (2 . "b") (2 . "c") (1 . "a") (1 . "b") (1 . "c"))
> (cartesian-product (list "c" "a" "b") (list 2 1))
'(("c" . 2) ("c" . 1) ("a" . 2) ("a" . 1) ("b" . 2) ("b" . 1))
> (cartesian-product (list "a" "b") (list 2 1))
'(("a" . 2) ("a" . 1) ("b" . 2) ("b" . 1))
> (cartesian-product (list 1) (list "a"))
'((1 . "a"))
> (cartesian-product null (list "a" "b" "c"))
'()

Submission

Submit: The course staff will collect your work directly from your hosted repository. To submit your work:

Make sure you have committed your latest changes.
```
$ git add ...
$ git commit ...
```
Run the command cs251 sign to sign your work and respond to any assignment survey questions.
```
$ cs251 sign
```
Push your signature and your latest local commits to the hosted repository.
```
$ git push
```

Confirm: All local changes have been submitted if the output of git status shows both:

Your branch is up to date with 'origin/master', meaning all local commits have been pushed
nothing to commit, meaning all local changes have been committed

Resubmit: If you realize you need to change something later, just repeat this process.

Lists of Pros and Cons

Contents