CS307: Synthetic Cameras
Plan
- Review solution to the Scale-of-Justice exercise
- Recap and questions: synthetic camera and perspective projection
- (paper/pencil) Exercise on perspective projection
- Recap and questions: Projection matrices
- Recap and questions: Three.js Camera API and camera tutor demo
- Exercises on setting up a camera
Pinhole and Synthetic Cameras
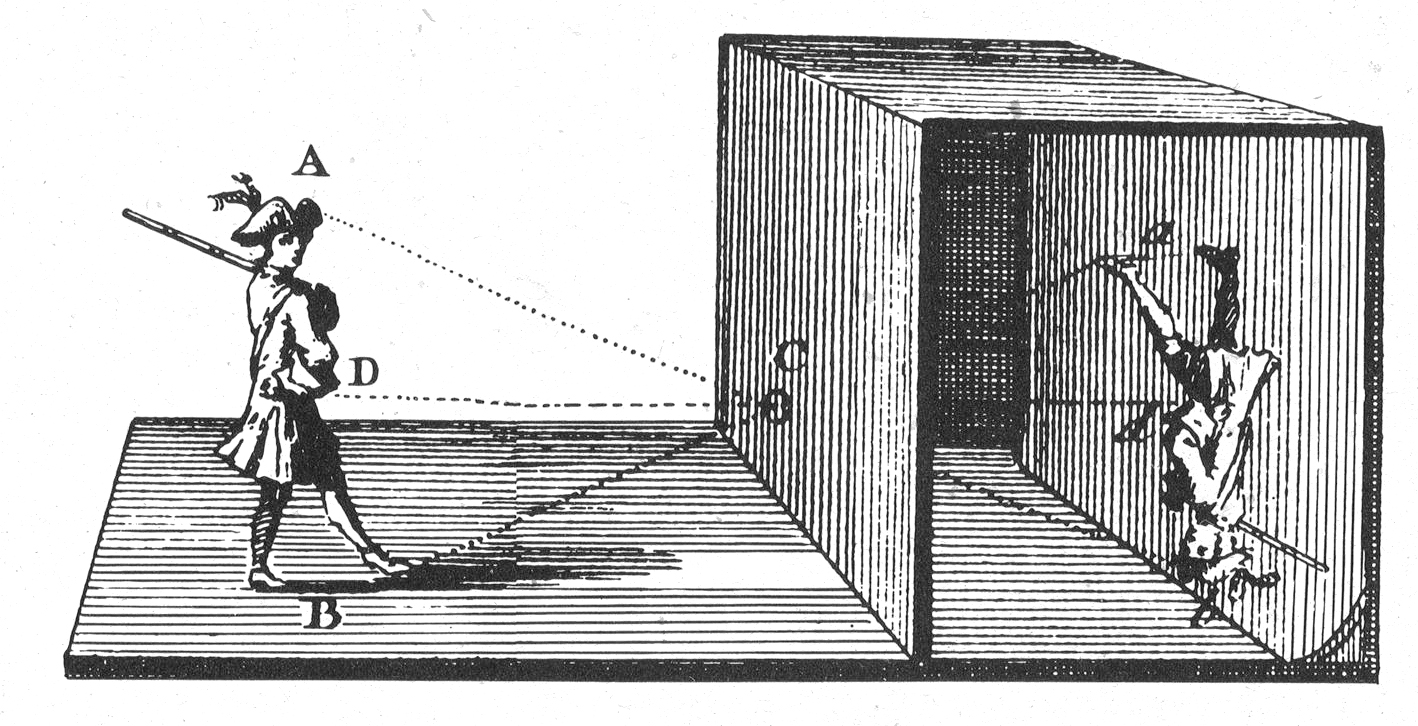
Pinhole camera, aka camera obscura:
Pinhole camera with object and its projection:
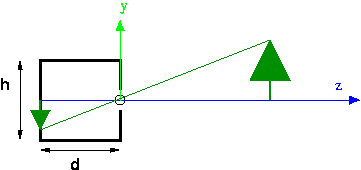
Pinhole camera showing similar triangles:
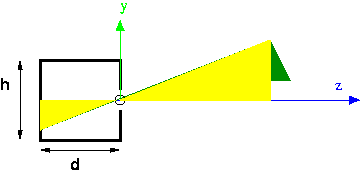
The synthetic camera moves the image plane in front of the center of projection to eliminate negatives:
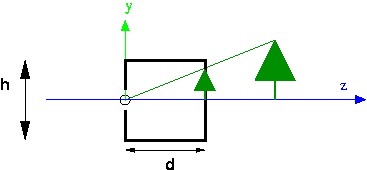
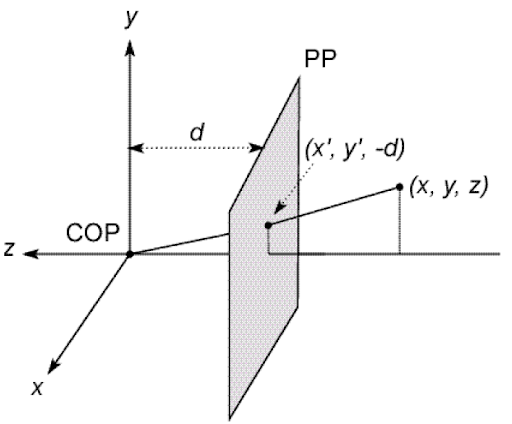
We'll use $(X,Y,Z)$ to refer to the 3D coordinates of a point in space, and $(x,y,z)$ to refer to the projected image coordinates. In the above diagram, the negative $z$ axis points to the right, so $z=-d$.
Consider the $y$ coordinate in the above pictures. Using similar triangles, $Y/Z = y/d$, so $y = d(Y/Z)$, which can be written as $y = Y/(Z/d)$
We can derive an expression for $x$ in a similar way: $x = X/(Z/d)$
Exercise: Perspective Projection
Assume a synthetic camera with the image plane (near plane) at a distance d from the center of projection (COP). Suppose the scene contains a tree of height H at a distance D from the COP. What is the height of the projected tree?
d*(H/D) or H*(d/D)
Perspective: projections shrink with distance. This also gives us vanishing points — think about railroad tracks.
Example: With the standard camera (COP at the origin, looking down the negative Z axis) and the image plane at Z=-3, find the projection of (7,8,-9).
Bird's eye view:
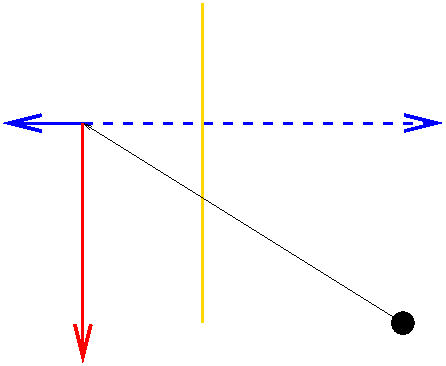
For X:
X/x = Z/z
7/x = -9/-3
7/(-9/-3) = x
x = 7/3
For Y:
Y/y = Z/z
8/y = -9/-3
8/(-9/-3) = y
y = 8/3
For the entire point, P:
projection of P
= (7/3, 8/3, -3)
= (1/3) * P
and 1/3 is just 1/near, where "near" is the distance from the COP to the image plane
Projection Matrices
We've been focusing on perspective projection, which was used to generate the drawing below:

The following two images illustrate orthographic projection:
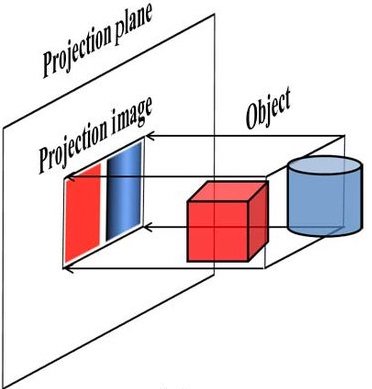
For orthographic projection, $(x,y,z) = (X,Y,0)$
Both projections can be implemented with matrix multiplication.
Orthographic Projection
\[ \left[ \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] \vecIV{X}{Y}{Z}{1} \]What does this do to a point $(X, Y, Z)$?
Perspective Projection
\[ \vecIV{X}{Y}{Z}{Z/d} = \left[ \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1/d & 0 \end{array} \right] \vecIV{X}{Y}{Z}{1} \]To obtain the projected image coordinates, $(x, y, z)$, we divide the result on the left by $Z/d$ (the perspective division step), yielding the following:
\[ \vecIV{x}{y}{z}{w} = \vecIV{X/(Z/d)}{Y/(Z/d)}{d}{1} \]
Note that \(d\) is the near distance: the distance from
the COP (center of projection) to the image plane. (We'll think of
$d$ as a positive quantity here)
Camera Setup in Three.js
The diagram below summarizes the key elements of the camera setup:
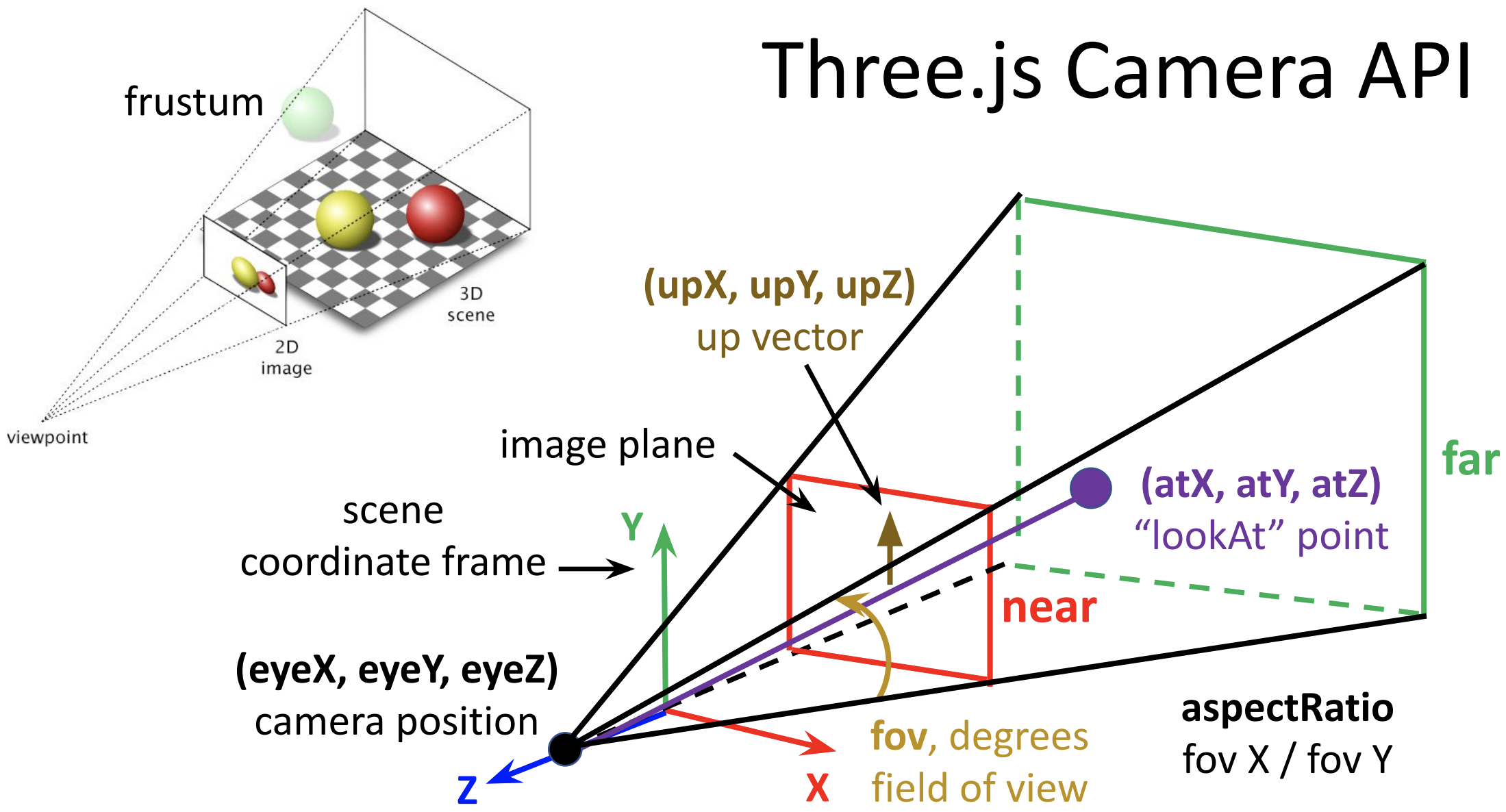
In the above code example, the camera parameters (adjusted in the GUI) are stored in
an object named cameraParams:
var cameraParams = {
near: 5,
far: 30,
fov: 75, // degrees
aspectRatio: 400.0/300.0, // from canvas dimensions, see CSS
atX: 0,
atY: 0,
atZ: 0,
eyeX: 0,
eyeY: 0,
eyeZ: 25,
upX: 0,
upY: 1,
upZ: 0
};
The following code defines a function named setupCamera() that creates
a camera with the desired parameters, and then invokes the function and adds the camera
to a scene:
function setupCamera (cameraParameters) {
// set up an abbreviation
var cp = cameraParameters;
// create an initial camera with the desired shape
var camera = new THREE.PerspectiveCamera(cp.fov,
cp.aspectRatio,
cp.near,
cp.far);
// set the camera location and orientation
camera.position.set(cp.eyeX, cp.eyeY, cp.eyeZ);
camera.up.set(cp.upX, cp.upY, cp.upZ);
camera.lookAt(new THREE.Vector3(cp.atX, cp.atY, cp.atZ));
return camera;
}
var camera = setupCamera(cameraParams);
scene.add(camera);
Note that you also need to do something like this at the end of your code:
function render() {
// assume global variables scene, renderer, and camera
renderer.render(scene,camera);
}
render();
TW's camera setup did this for us automatically. With this code, though, we can cut the TW apron strings.
Question: Can we set up multiple cameras in the same scene? Not really, but see this example from the Three.js site
Exercises: Creating Desired Camera Views
Exercise: Setting up a Camera
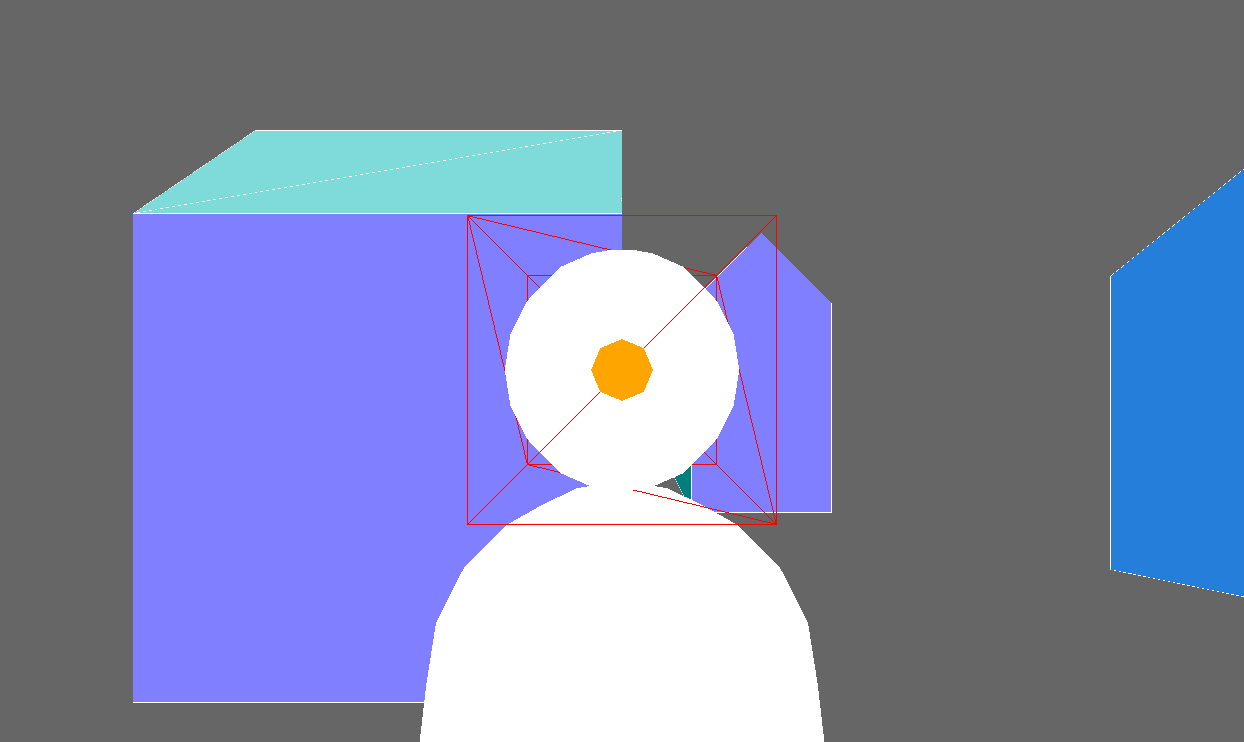
Using this town-view-before.html, set up a camera to view the snowman from above and to the right. Something like this:
- You might find it helpful to use the following town-view-gui.html .
- Define a function to set up the camera the way you want.
- Replace
TW.cameraSetup()with your new camera.
Your result might look like town-view.html
Exercise: Zooming vs. Dollying
Is there any difference between
- zooming in, keeping the eye point the same and reducing the FOV
- dollying in, keeping the FOV the same and moving the camera closer
Let's try to experience the effects of these changes to the camera setup.
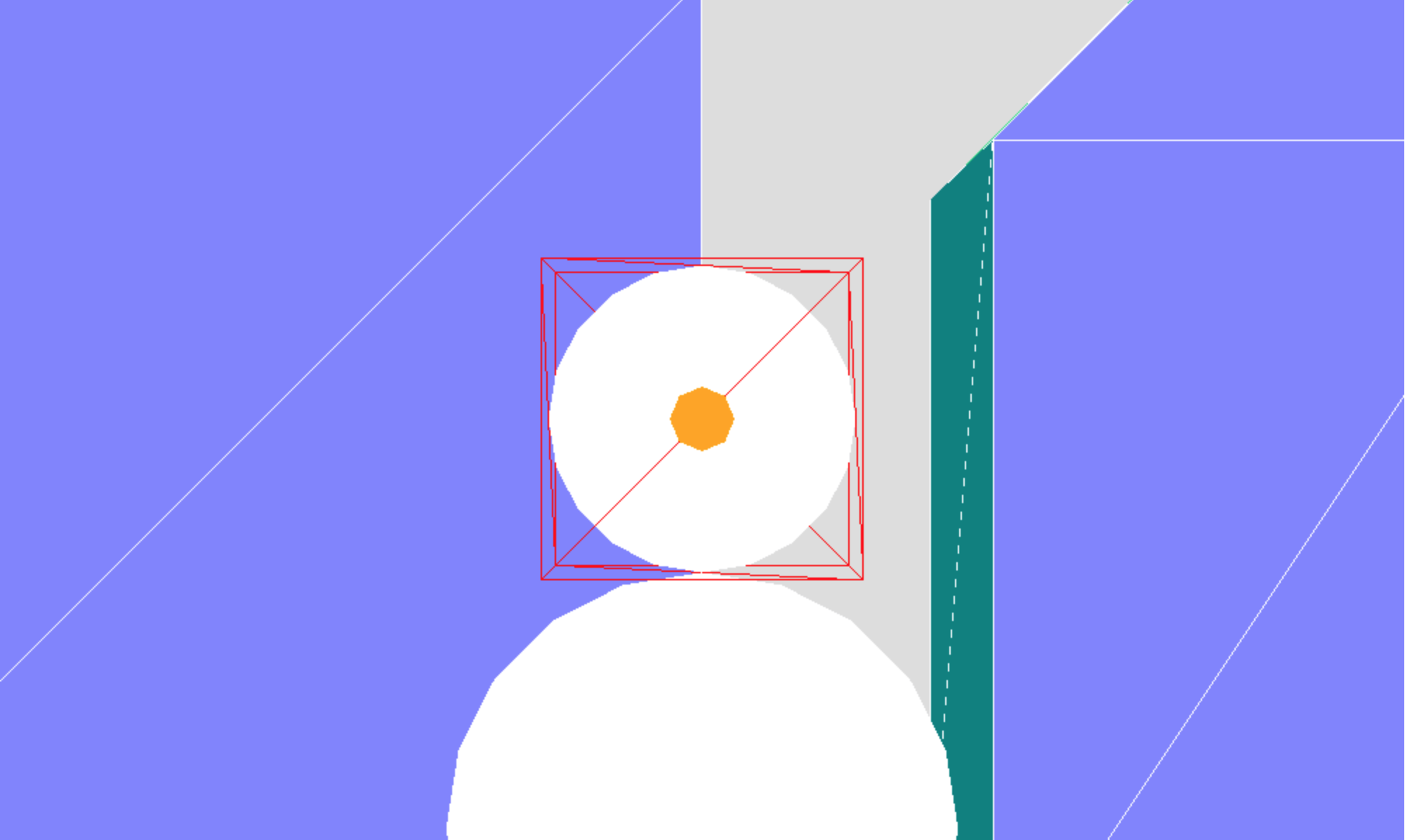
To begin, add a wireframe box to the scene that fits snuggly around the head of the snowman. Then try to set the camera parameters so that the scene appears like this:
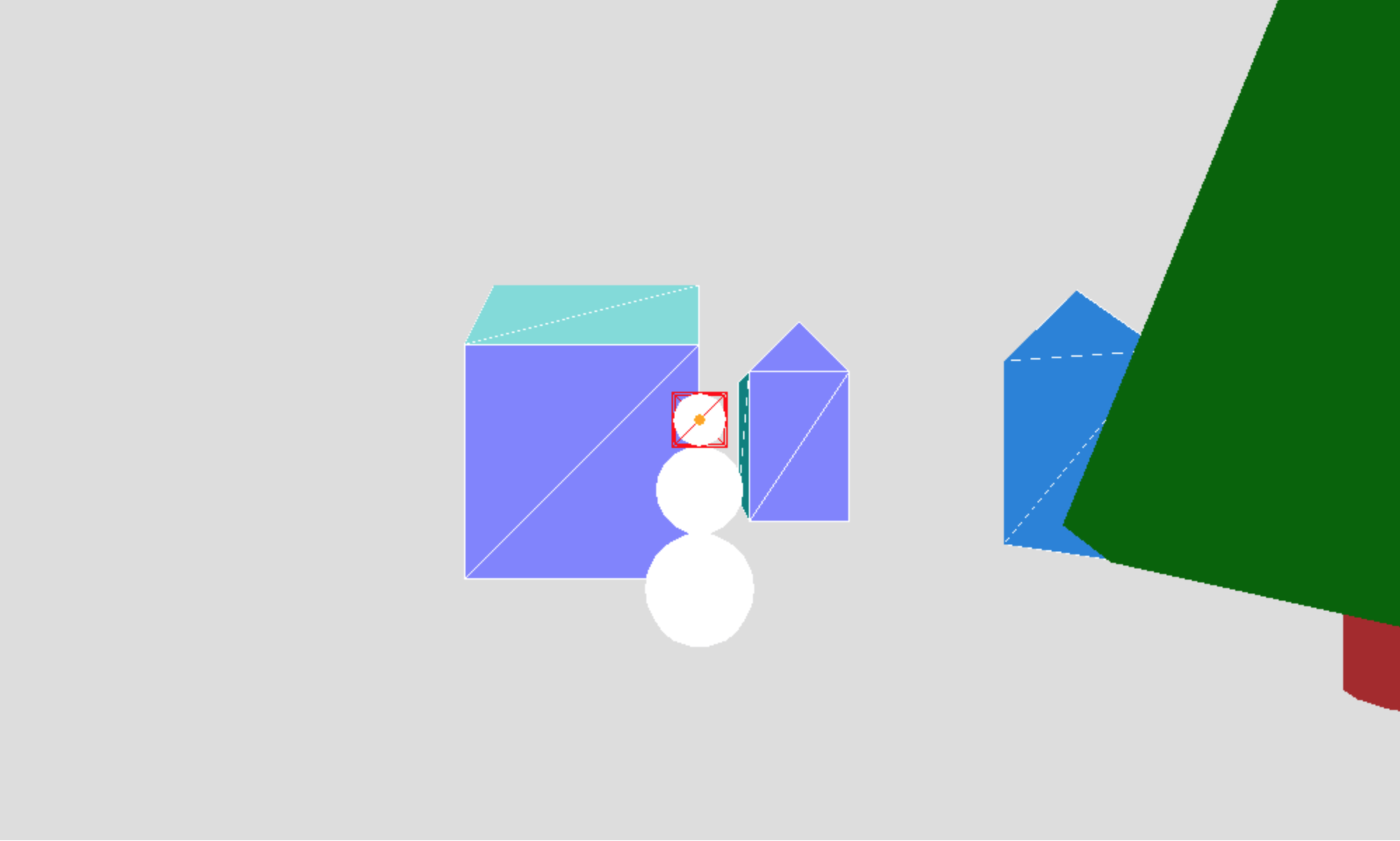
Hints: the camera is positioned 5 units in front of the center of
the snowman's head (at the same x and y coordinates as this center point) and is
looking at this center point. Set the fov to achieve the
above appearance.
Then try to set the camera parameters to reproduce each of the following views, dollying in to create one of the views and zooming in to create the other:
Which figure was created by zooming, and which by dollying?
Your solutions might be like snowman-close.html and snowman-zoom.html.
Vup
Most of the time, Vup is very simple: we have \[ V_\mathrm{up} = (0, 1, 0) \]
The minute we want something different, though, Vup can be confusing. Try to imagine it this way:
- Visualize the Vup vector in 3D space, along with the image plane.
- Project the Vup vector onto the image plane
- The frustum spins around the VPN (view plane normal) so that the Vup vector is parallel to the left/right edges.
- When the top of the frustum is mapped onto the canvas, the Vup vector is parallel to the left/right edge of the canvas.
There are two important consequences of the way Vup works:
- The Vup vector can't project to a point, which means it can't be parallel or anti-parallel to the VPN.
- Any change to the Vup vector that doesn't change the direction of its projection on the image plane doesn't affect anything. The image is still oriented the same way.
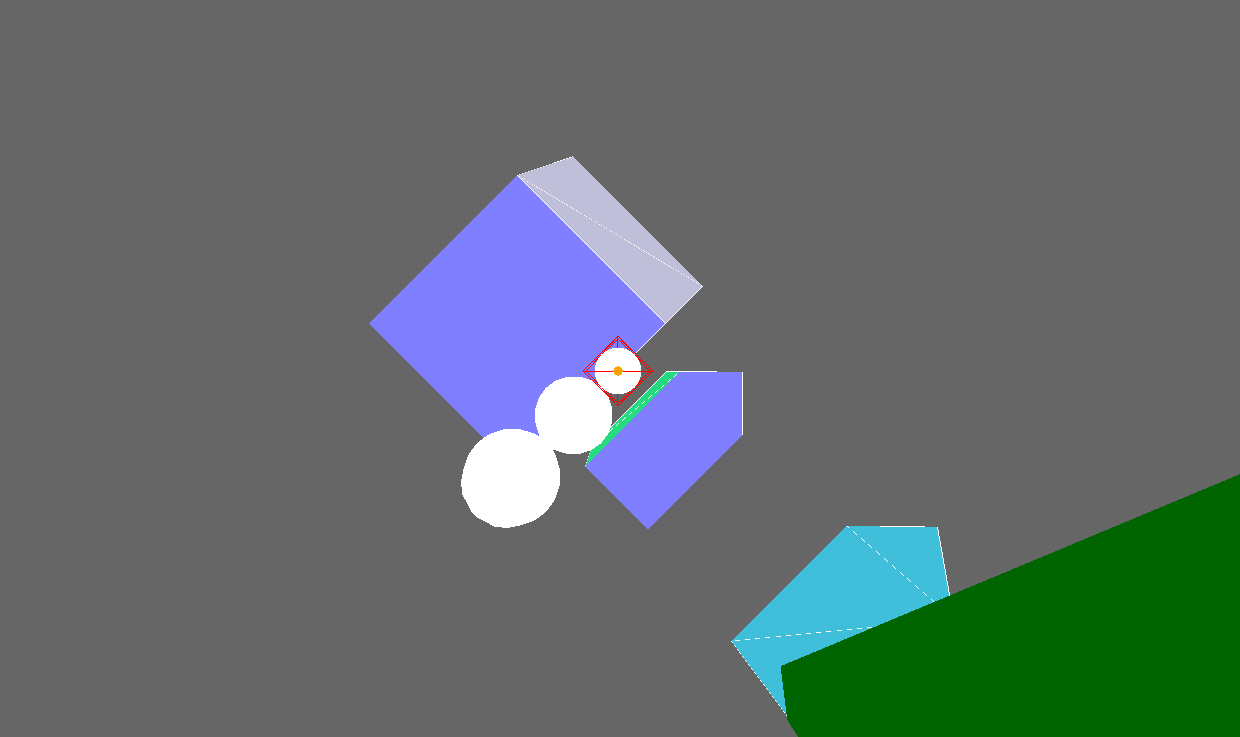
Exercise: Changing Vup
Let's try to experiment with changing Vup
Try to reproduce both of the following:
- Think about what Vup might be.
- Set up the camera for each scene.
Your solutions might be like snowman-close-angled.html and snowman-close-overhead.html.
Exercise: Viewing the Barn
The goal of this exercise is to mimic a set of views of a wireframe barn, shown in the following code (you won't be able to see the actual solution code here): barnviews-solution.html
When viewing this page, type any of the keys numbered 1 to 5, and a new view of the barn will appear. In this exercise, you'll try to duplicate my camera location and orientation as closely as possible, by analyzing how things are projecting to see if you can reverse-engineer to set up a similar camera. This will help you when you are trying to achieve a particular look in your own scenes.
The starting point for this exercise is this barnviews-start.html code file
Carefully examine the starter code to understand the dimensions of the barn and initial camera information that's provided. For each of the 5 views, add two code statements to set the position and the up vector for the camera, to create a view that is as close as possible to the solution.
Here's a solution with JS code that you can view: barnviews.html
Preparation for Next Time
Next time, we'll look at how we create surface with different material properties, such as dull or shiny surfaces, and how we add light sources to a graphical scene. To prepare:
- Reading for Monday: Material and Lighting
- Submit Sakai Quiz by Sunday evening at 9:00 pm EST — you'll have an hour to complete the quiz, which is "open book/notes"
Due on Friday at 11:00 pm EST: HWK2: Clown