CS307: HSL, Color Interpolation, and the Instance Transform

Plan

Recap and questions: HSL and HSV color models
Recap and questions: Parametric triangles and color interpolation
Exercise: Colorful stars
Recap and questions: Instance transform & barn demo
- built-in Three.js geometries
Exercises: Build a town with houses, tree, and snow
Exercise: Luxo lamp

HSL and HSV Color Models

HSV and HSL are common, useful color models. Hue and Saturation are the same for both models. Value and Lightness are similar. For humans, these models are more intuitive than RGB.

Three.js provides support for HSL and there are many online tools for selecting HSL colors. In the example below, the setHSL() method is used to specify hue, saturation, and lightness values for a color. Note that each of these quantities must be converted to a range from 0.0 to 1.0.

var myColor = new THREE.Color();
myColor.setHSL(0.6, 0.9, 0.8);
alert("myColor is " + myColor.getHexString());

This text is displayed with myColor as background.

The CMYK model is good to know about, but won't be used in this course.

Parametric Triangles and Color Interpolation

So far, we displayed faces with solid color. Suppose we want to specify different colors for the vertices and display smoothly varying color over a face. To understand how this is done, we need to know how to describe a triangle using parametric equations.

The parametric equation of a triangle defines an area that is created from a vertex and a line segment, using a parametric equation between the vertex and a point on the line segment, where the point on the line segment is itself defined by a parametric equation.

Two parametric lines, one of which is an endpoint of the other, create a parametric triangle

The equation Q(s,t) can also be expressed as:

\[ Q(s,t) = A(1-t)s+Bts + C(1-s) \]

We can think of this as a weighted sum of the coordinates of the three vertices:

Q = A * wa + B * wb + C * wc
wa + wb + wc = 1
0 ≤ wa, wb, wc, ≤ 1

Suppose we have three vertices A,B,C with x,y,z coordinates shown in the following diagram, and want to compute the coordinates of a point D inside the triangle, where t = 0.25 and s = 0.67? The steps of this calculation are shown below the diagram.

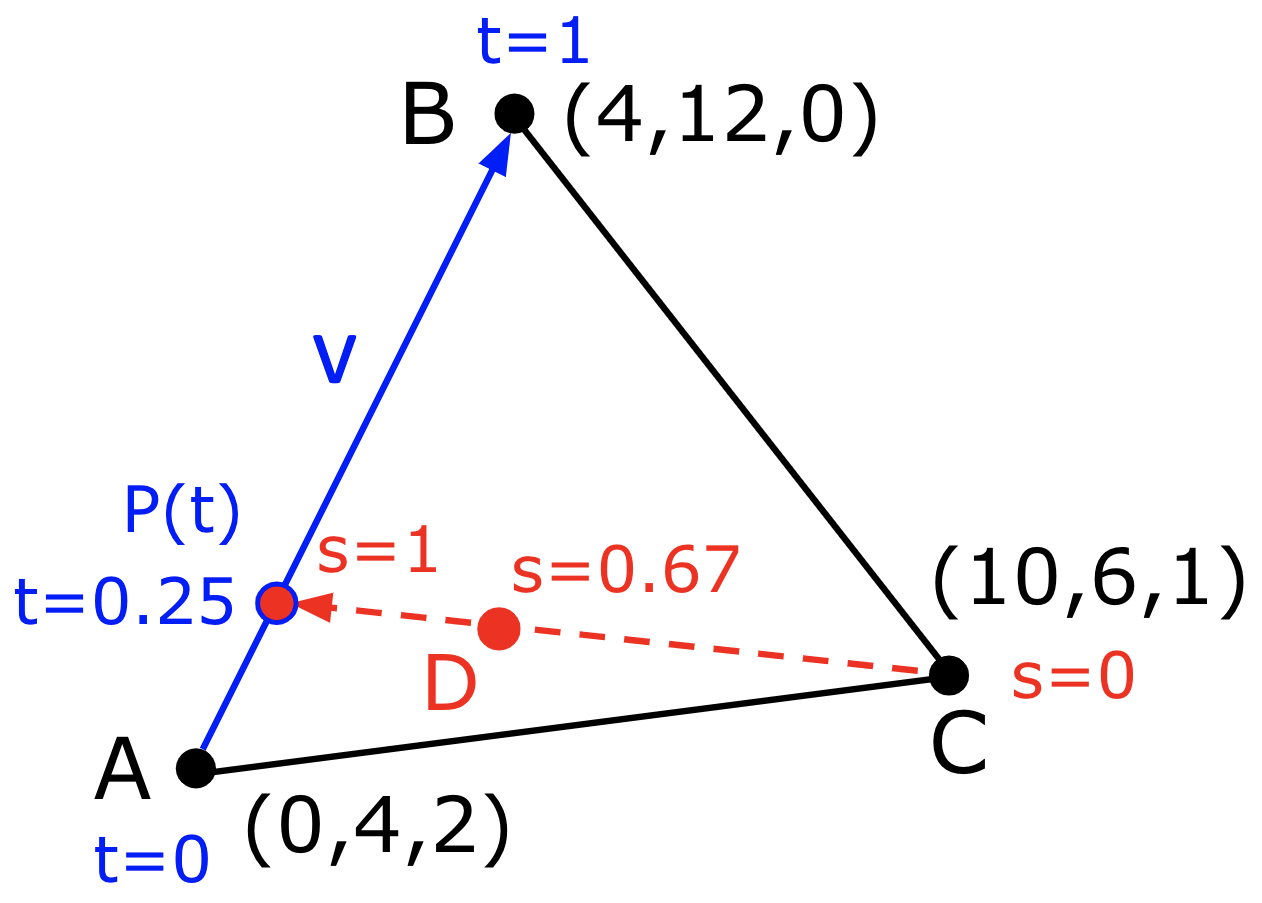
Q(s,t) = A(1-t)s + Bts + C(1-s) Q(2/3,1/4) = (0,4,2)(3/4)(2/3) + (4,12,0)(1/4)(2/3) + (10,6,1)(1/3) D = (0,4,2)(1/2) + (4,12,0)(1/6) + (10,6,1)(1/3) D = (0,2,1) + (2/3,2,0) + (10/3,2,1/3) D = (4,6,4/3)

Now suppose the vertices A,B,C have different colors, and we want to determine a color for the point D within the triangle that "blends" together the colors of the vertices? In particular, suppose A is yellow, B is green, and C is cyan. How can we calculate the color of D?

color = (color of A)(1-t)s + (color of B)ts + (color of C)(1-s) (r,g,b) = (1,1,0)(3/4)(2/3) + (0,1,0)(1/4)(2/3) + (0,1,1)(1/3) (r,g,b) = (1,1,0)(1/2) + (0,1,0)(1/6) + (0,1,1)(1/3) (r,g,b) = (1/2,1/2,0) + (0,1/6,0) + (0,1/3,1/3) (r,g,b) = (1/2,1,1/3) = (0.5,1,0.33)

Color Interpolation in Three.js

There are three key elements for doing color interpolation over triangles in Three.js:

the vertexColors attribute of the geometry is an array of colors
each THREE.Face3 object contains an array of three colors, also named vertexColors, with one color for each vertex in the face
in the THREE.MeshBasicMaterial object, we set the vertexColors attribute to the magic constant THREE.VertexColors

We'll explore these ideas with our colorful square. Below are diagrams and essential code for this example. The TW.computeFaceColors() function creates the vertexColors arrays that are stored for each face in the geometry:

var squareGeom = new THREE.Geometry();
squareGeom.vertices = [new THREE.Vector3(0,0,0),  // vertices
                       new THREE.Vector3(1,0,0),
                       new THREE.Vector3(1,1,0),
                       new THREE.Vector3(0,1,0)];
squareGeom.faces = [new THREE.Face3(0,1,3),      // faces
                    new THREE.Face3(1,2,3)];

// define the colors for each of the four vertices
squareGeom.vertexColors = [new THREE.Color("magenta"),
                           new THREE.Color("blue"),
                           new THREE.Color("red"),
                           new THREE.Color("green")];

// setup the vertex colors for each face
TW.computeFaceColors(squareGeom);

// create a material that uses vertex colors
// and interpolated color within faces
var squareMaterial = new THREE.MeshBasicMaterial(
                           {vertexColors: THREE.VertexColors} );

// create a mesh and add to the scene
var squareMesh = new THREE.Mesh(squareGeom, squareMaterial);
scene.add(squareMesh);

Exercise: Colorful Stars

This stars-start.html code file contains a function named starGeometry() that creates and returns a Three.Geometry object for a three-pointed star.

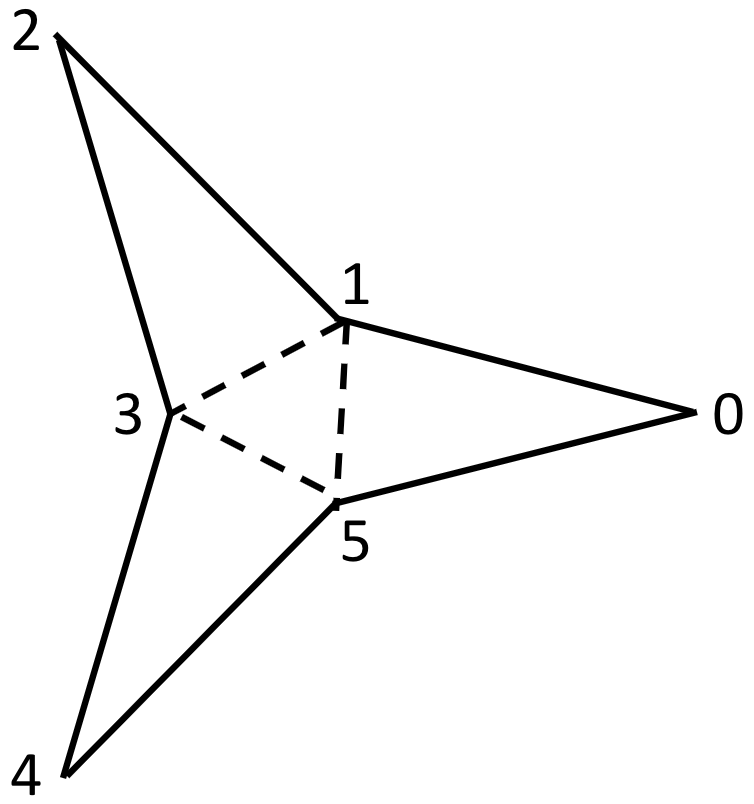
This diagram shows the order in which the vertices and colors are defined, and placement of faces:

Modify the code to create a star that uses color interpolation of the triangular faces, and adds it to the scene. Your star might look like this:

Some tips:

The starting code includes an array of THREE.Color objects named colors. Feel free to change the colors to whatever you want!
When creating the material for the star using THREE.MeshBasicMaterial, add a second property to the input object (in addition to the vertexColors property) that tells Three.js to render both sides of the triangular faces:
side: THREE.DoubleSide

Here's a possible solution: stars1.html

(Optional) Add six additional stars to the scene that each have a uniform color, and which are placed around the central star, something like this:

Some tips for this part:

Think about how this can be done with a loop
Use the same array of colors that you used for the central star
Recall that position.set() can be used to place a mesh at a desired location
Remember to adjust the bounding box supplied to TW.cameraSetup() to see the additional stars

Your code might look like this: stars.html

The Instance Transform

Built-in objects (e.g. boxes, spheres, cylinders) are very useful. They use polygonal approximations to smooth shapes.

We place objects with

position (translation) along major axes (x,y,z):
- obj.position.set(a,b,c)
- obj.position.x = d
rotation around major axes (angles are specified in radians):
- obj.rotation.set(alpha,beta,gamma)
- obj.rotation.y = theta
scale along major axes:
- obj.scale.set(i,j,k)
- obj.scale.z = m
It can also be useful to rotate an object around an arbitrary axis. The normalize() method converts a vector to a unit vector, with length 1 (Three.js requires this):
```
var axis = new THREE.Vector3(3,4,5);
axis.normalize();
obj.rotateOnAxis(axis,radians);
```
These settings are applied to the object and all its descendants (more on this next time), which is a very powerful idea.
Let's explore these ideas with the barn instance transform demo
Exercises: Building a Town
Build a "town" consisting of just three houses. Here's the layout of the town:

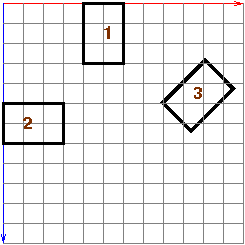
Here's an initial town0.html to get you started
1. Figure out your scene's bounding box
2. Place the first house. Remember the following functions used in the barn example:
  - TW.createBarn(w,h,d)
  - TW.createMesh(geom)
3. Place two more houses
Your finished town might look like this:

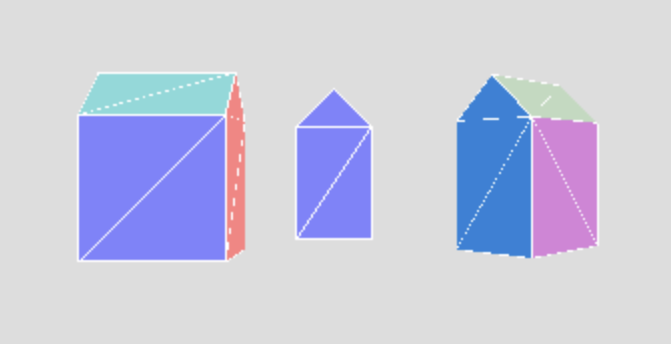
A solution for this part: town1.html
Town with tree

Add a tree to the scene. A tree can just be a green cone and brown trunk, created with THREE.ConeGeometry and THREE.CylinderGeometry

The trick with this is to get the dimensions and positioning right.
Also recall that THREE.Mesh and THREE.MeshBasicMaterial can be used to set up the colors of the tree.
Your finished town might look like this:

Code solution with the added tree: town2.html

Town with tree and snow

Using a THREE.PlaneGeometry, add a blanket of snow to the town, as shown below from a couple points of view:

Code for the final town: town3.html

Exercise: Building Your Own Luxo Lamp
Starting with luxo-start.html, add code to create a basic Luxo lamp using the built-in Three.js geometries and the instance transform. The starting code creates an array of THREE.MeshBasicMaterial objects to use for the colors of the lamp.
Your result might look something like the pictures below (the camera is rotated in the right picture, to see the light bulb inside the lamp):

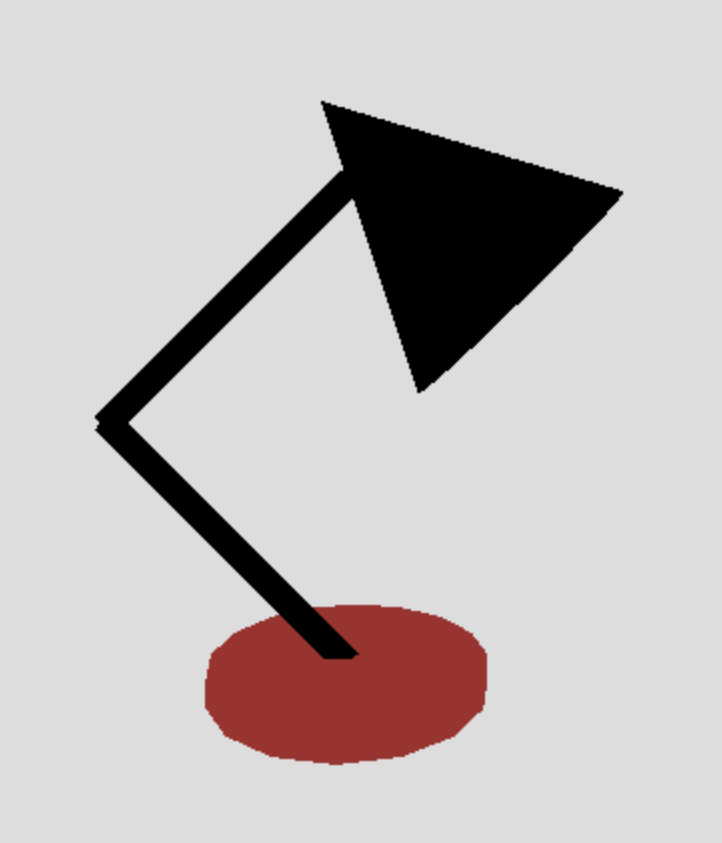
A couple tips:
- Check the Three.js documentation for THREE.ConeGeometry to see how you can render the cone for the lamp so that its base is "open"
- Choose a convenient "origin" for the object in the scene coordinate frame. It's ok to estimate the size and position of subparts of the lamp, and use numbers in your code (it may take some trial-and-error to get things right!)
A possible solution: luxo.html
Next Time

Note how difficult the position-setting was for some components of the town and Luxo lamp. Next time, we'll learn how to build composite objects — objects with constituent parts such as this — which will facilitate the positioning of the object parts and placement of a composite object anywhere in the scene.
To prepare:
- Reading for Monday: Nested Transforms and Affine Math
- Submit Sakai Quiz by Sunday evening at 9:00 pm EST — you'll have an hour to complete the quiz, which is "open book/notes"
Due Friday at 11 pm EST: HWK1: Obelisk