\( \newcommand{\vecIII}[3]{\left[\begin{array}{c} #1\\#2\\#3 \end{array}\right]} \newcommand{\vecIV}[4]{\left[\begin{array}{c} #1\\#2\\#3\\#4 \end{array}\right]} \newcommand{\Choose}[2]{ { { #1 }\choose{ #2 } } } \newcommand{\vecII}[2]{\left[\begin{array}{c} #1\\#2 \end{array}\right]} \newcommand{\vecIII}[3]{\left[\begin{array}{c} #1\\#2\\#3 \end{array}\right]} \newcommand{\vecIV}[4]{\left[\begin{array}{c} #1\\#2\\#3\\#4 \end{array}\right]} \newcommand{\matIIxII}[4]{\left[ \begin{array}{cc} #1 & #2 \\ #3 & #4 \end{array}\right]} \newcommand{\matIIIxIII}[9]{\left[ \begin{array}{ccc} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9 \end{array}\right]} \)

CS307: HSL/HSV Color Models and Color Interpolation

Plan

  • HSL and HSV color models
  • Parametric lines and triangles
  • Color interpolation
  • Quiz questions
  • Exercise: Colorful stars

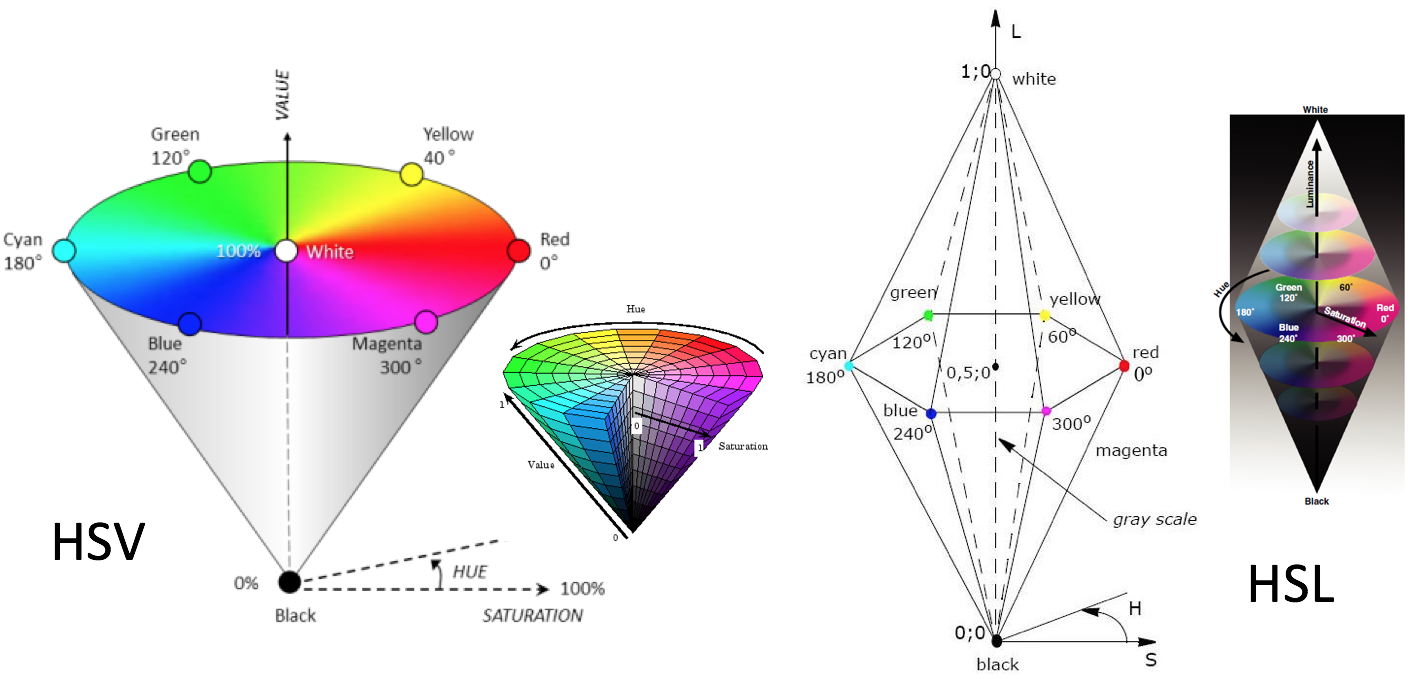
HSL and HSV Color Models

HSV and HSL are common, useful color models. Hue and Saturation are the same for both models. Value and Lightness are similar. For humans, these models are more intuitive than RGB.

Three.js provides support for HSL and there are many online tools for selecting HSL colors. In the example below, the setHSL() method is used to specify hue, saturation, and lightness values for a color. Note that each of these quantities must be converted to a range from 0.0 to 1.0. 

var myColor = new THREE.Color();
myColor.setHSL(0.6, 0.9, 0.8);
alert("myColor is " + myColor.getHexString());

This text is displayed with myColor as background.

The CMYK model is good to know about, but won't be used in this course.

Parametric Triangles and Color Interpolation

So far, we displayed faces with solid color. Suppose we want to specify different colors for the vertices and display smoothly varying color over a face. To understand how this is done, we need to know how to describe a triangle using parametric equations.

The parametric equation of a triangle defines an area that is created from a vertex and a line segment, using a parametric equation between the vertex and a point on the line segment, where the point on the line segment is itself defined by a parametric equation.

Two parametric lines, one of which is an endpoint of the other, create a parametric triangle

The equation Q(s,t) can also be expressed as:

\[ Q(s,t) = A(1-t)s+Bts + C(1-s) \]

We can think of this as a weighted sum of the coordinates of the three vertices: 

Q = A * wa + B * wb + C * wc
wa + wb + wc = 1
0 ≤ wa, wb, wc, ≤ 1

Suppose we have three vertices A,B,C with x,y,z coordinates shown in the following diagram, and want to compute the coordinates of a point D inside the triangle, where t = 0.25 and s = 0.67? The steps of this calculation are shown below the diagram.

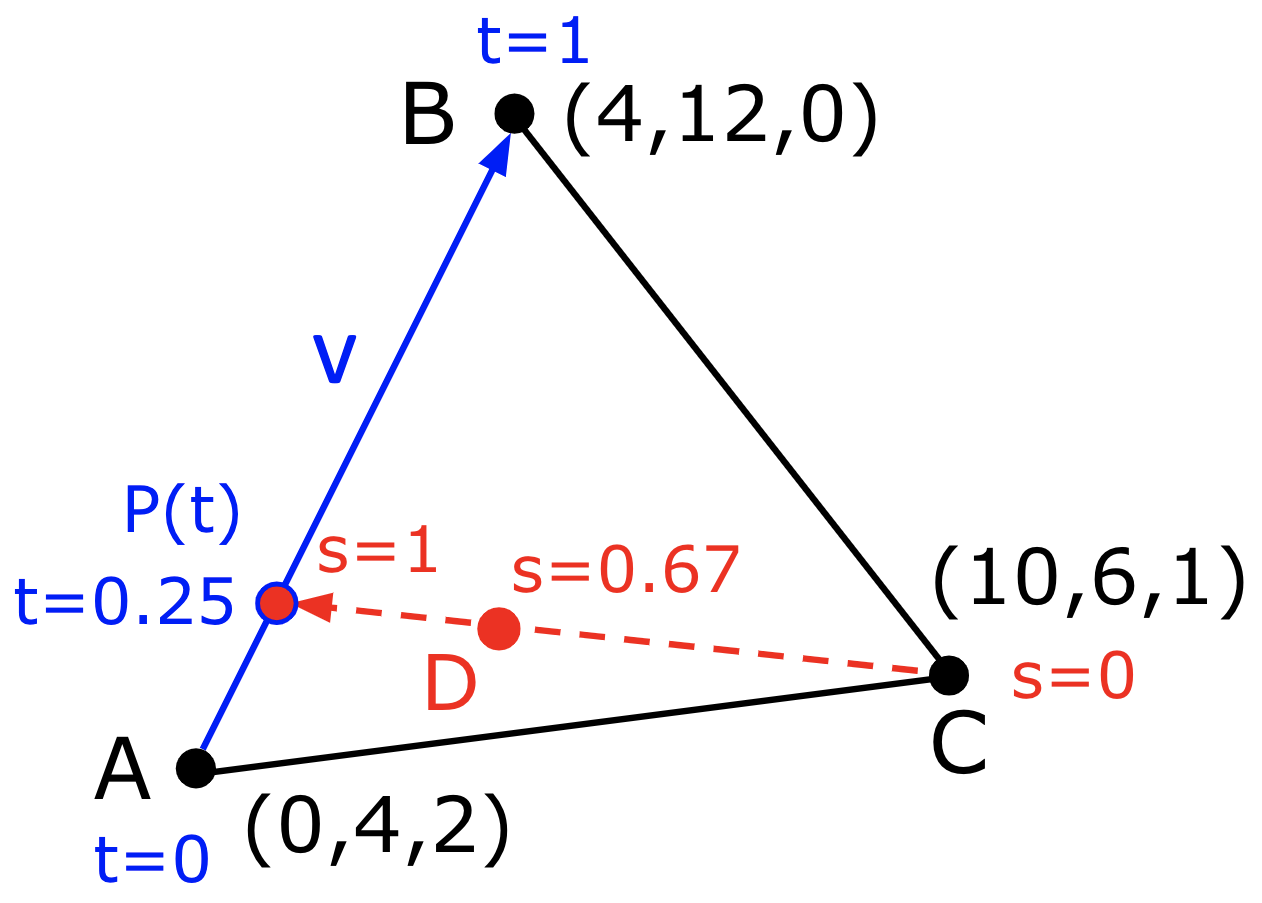
Q(s,t) = A(1-t)s + Bts + C(1-s)
Q(2/3,1/4) = (0,4,2)(3/4)(2/3) + (4,12,0)(1/4)(2/3) + (10,6,1)(1/3)
D = (0,4,2)(1/2) + (4,12,0)(1/6) + (10,6,1)(1/3)
D = (0,2,1) + (2/3,2,0) + (10/3,2,1/3)
D = (4,6,4/3)

Now suppose the vertices A,B,C have different colors, and we want to determine a color for the point D within the triangle that "blends" together the colors of the vertices? In particular, suppose A is yellow, B is green, and C is cyan. How can we calculate the color of D?

color = (color of A)(1-t)s + (color of B)ts + (color of C)(1-s)
(r,g,b) = (1,1,0)(3/4)(2/3) + (0,1,0)(1/4)(2/3) + (0,1,1)(1/3)
(r,g,b) = (1,1,0)(1/2) + (0,1,0)(1/6) + (0,1,1)(1/3)
(r,g,b) = (1/2,1/2,0) + (0,1/6,0) + (0,1/3,1/3)
(r,g,b) = (1/2,1,1/3) = (0.5,1,0.33)

Color Interpolation in Three.js

There are three key elements for doing color interpolation over triangles in Three.js:

  • the vertexColors attribute of the geometry is an array of colors
  • each THREE.Face3 object contains an array of three colors, also named vertexColors, with one color for each vertex in the face
  • in the THREE.MeshBasicMaterial object, we set the vertexColors attribute to the magic constant THREE.VertexColors

Color Hexcones

Let's take a minute to look at the Color Cones demo.

Color Interpolation

We'll explore these ideas with our colorful square. Below are diagrams and essential code for this example. The TW.computeFaceColors() function creates the vertexColors arrays that are stored for each face in the geometry:

       

function squareGeometry () {
  var squareGeom = new THREE.Geometry();
  squareGeom.vertices = [new THREE.Vector3(0,0,0), // vertices
                         new THREE.Vector3(1,0,0),
                         new THREE.Vector3(1,1,0),
                         new THREE.Vector3(0,1,0)];
  squareGeom.faces = [new THREE.Face3(0,1,3),   // faces
                      new THREE.Face3(1,2,3)];
  return squareGeom;
}
var squareGeom = squareGeometry();   // create geometry

// define the colors for each of the four vertices
squareGeom.vertexColors = [new THREE.Color("magenta"),
                           new THREE.Color("blue"),
                           new THREE.Color("red"),
                           new THREE.Color("green")];

// setup the vertex colors for each face
TW.computeFaceColors(squareGeom);

// create a material that uses vertex colors
// and interpolated color within faces
var squareMaterial = new THREE.MeshBasicMaterial(
                          {vertexColors: THREE.VertexColors,
                                   side: THREE.DoubleSide} );

// create a mesh and add to the scene
var squareMesh = new THREE.Mesh(squareGeom, squareMaterial);
scene.add(squareMesh);

Quiz Questions

I'll cover as many of your quiz questions as I can.

Exercise: Colorful Stars

This stars-start.html code file contains a function named starGeometry() that creates and returns a Three.Geometry object for a three-pointed star.

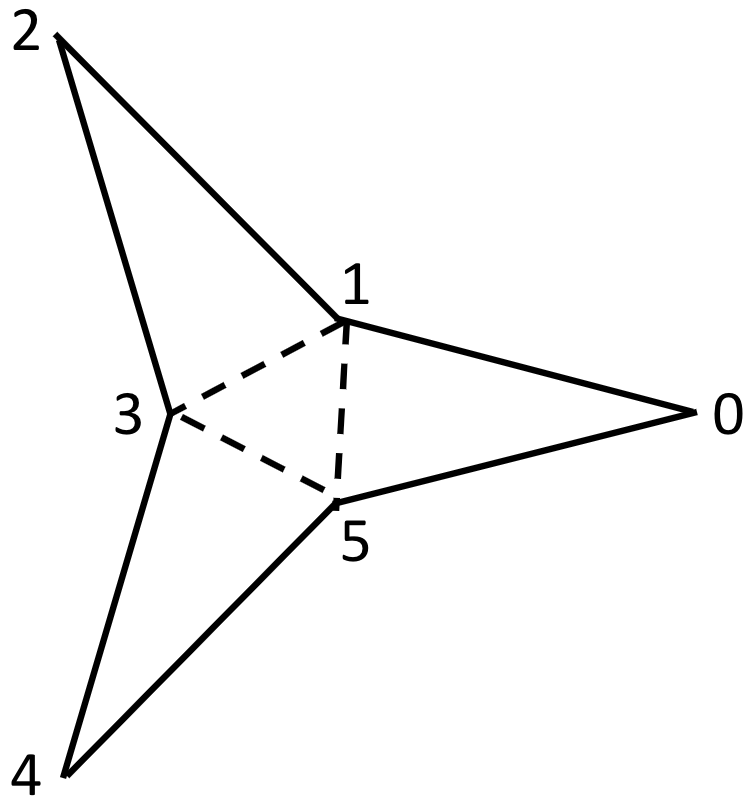
This diagram shows the order in which the vertices and colors are defined, and placement of faces:

Modify the code to create a star that uses color interpolation of the triangular faces, and adds it to the scene. Your star might look like this:

Some tips:

  • The starting code includes an array of THREE.Color objects named colors. Feel free to change the colors to whatever you want!
  • When creating the material for the star using THREE.MeshBasicMaterial, add a second property to the input object (in addition to the vertexColors property) that tells Three.js to render both sides of the triangular faces:

        side: THREE.DoubleSide

Here's a possible solution: stars1.html

(Optional) Add six additional stars to the scene that each have a uniform color, and are placed around the central star, something like this:

Some tips for this part:

  • Think about how this can be done with a loop (Hint: The starGeometry() function has a loop example that may be handy)
  • Use the same array of colors that you used for the central star
  • Recall that position.set() can be used to place a mesh at a desired location
  • Remember to adjust the bounding box supplied to TW.cameraSetup() to see the additional stars

Your code might look like this: stars.html

To Do for Next Class