CS313

Project 8

How to turn in this Project

You are required to turn in both a hardcopy and a softcopy. If working as a team, the teamshould submit a single hardcopy and a single softcopy (to either team member's account). Please make sure to keep a copy of your work, on your computer, in your private directory (or, to play it safe, both).

Hardcopy Submission

Your hardcopy packet should consist of:
  1. The cover page.
  2. Your HMM.java file from Task 1.
  3. Your filled in Table Of Results from Tasks 2, 3, and 4.
  4. Your Ecoli_states.txt and Ecoli_transitions.txt file from Task 3.
  5. Your Yeast_states.txt and Yeast_transitions.txt file from Task 3.
  6. Your Arabidopsis_states.txt and Arabidopsis_transitions.txt file from Task 3.
  7. Your Fly_states.txt and Fly_transitions.txt file from Task 3.
  8. Your Ecoli_states.txt and Ecoli_transitions.txt file from Task 4.
  9. Your Yeast_states.txt and Yeast_transitions.txt file from Task 4.
  10. Your Arabidopsis_states.txt and Arabidopsis_transitions.txt file from Task 4.
  11. Your Fly_states.txt and Fly_transitions.txt file from Task 4.
Staple these together and submit them under the instructor's office door on the due date.

Softcopy Submission

You should submit your final version of your GeneFinder directory to the drop/project8 directory in your account on the CS server.

The phone rings for nearly two minutes before the sound of it brings you to consciousness. You look at the clock... it's 3:00am. Who could possibly be calling at this hour? Hello? Someone from the Mobile Foundation? No, that's the Nobel Foundation. Huh? Oh. Do they know it is 3:00am? They do. It is 8:00am in Stockholm. Oh. So, like, what's up, why are you calling? The Nobel Prize in Physiology or Medicine. Are you serious? They are very serious. Your mind is suddenly lucid. In your email, you are told, is an official letter from the Nobel Foundation congratulating you on your award. There will be a press release in a couple of hours. They are citing your work integrating computational and experimental sciences, your breakthrough research on how cells regulate oncogenes, the computational advances that you championed that have become the gold-standard for identifying genes in a genome, and your lifetime of contributions to science and medicine. Wow, you think. Overwhelmed, your mind races back to your days in college... your CS313 instructor wasn't right about much as you recall, but he did foretell this moment. Weird.

Background

In this project, your goal is to develop a gene-finder based on a hidden Markov model (HMM). In the first task, you will complete an implementation of a HMM. In the second, third, and fourth tasks, you will use the HMM as a gene-finder. Given a genomic sequence, your gene-finder should predict where any protein-coding genes can be found in the genomic sequence. More specifically, your gene-finder should indicate for each nucleotide in the genomic sequence whether the nucleotide is part of a protein-coding region (i.e., a gene) or not.

Once you have developed your gene-finder, you will predict the locations of genes in genomic sequences from several different species. You will then compare your predictions with the locations of known/documented genes in the species to evaluate how accurate your predictions are. The accuracy of your predictions will vary depending on the details of your HMM and on the species for which you are predicting genes (it is easier to identify genes in the genomes of some species than in others).

Task 1: Implementing a Hidden Markov Model (HMM)

We have provided you with a partial implementation of a HMM. The HMM implementation consists of two classes:

The contracts for these two classes can be found here.

An implementation for these two classes is stored in the download/GeneFinder subdirectory on the CS server.

Study the two provided classes, State and HMM. The HMM class contains code to read in from files information about a HMM:

The State class does not require any modification. However, the HMM class is incomplete. The HMM class does not contain code to determine the optimal annotation (i.e., parse or state sequence) for an observation sequence. In this task, you goal is to complete the implementation of the HMM class. To complete the HMM class, you will need to implement three methods described in the HMM contract, namely fillInTableEntry, viterbi, and determineOptimalAnnotation. These three methods, when completed, will enable computation of the optimal annotation of an observation sequence.

With the code available to download on the CS server, we have provided you with several files in the data_Examples directory for testing your HMM implementation. We have also provided you with a sample solution, TEST_HMM, which you can execute and compare to your own solution. For example, executing the sample solution with the three provided files corresponding to a HMM based on 3 coins might yield the following: 

[cs313@tempest GeneFinder] java TEST_HMM data_Examples/coin_states.txt data_Examples/coin_transitions.txt data_Examples/coin_observation.txt

Optimal annotation:

                HTTHTTTHHT       10
                1222222222


Score of optimal annotation:     -12.192816965761187

In the above example, the optimal annotation of the observation sequence HTTHTTTHHT has a score of -12.192816965761187 and can be achieved by flipping coin 1 once and then flipping coin 2 nine times.

As another example, executing the sample solution with the three provided files corresponding to a HMM based on three states emitting English letters might yield the following: 

[cs313@tempest GeneFinder] java TEST_HMM data_Examples/language_states.txt data_Examples/language_transitions.txt data_Examples/language_observation.txt

Optimal annotation:

                REMEMBEREVERREVERSEMEREVERBS     28
                1122111333333333311122112211


Score of optimal annotation:     -38.62118674370365

In the above example, the optimal annotation of the observation sequence REMEMBEREVERREVERSEMEREVERBS has a score of -38.6211867437036 and can be achieved by starting in state 1 and emitting the character R, transitioning to state 1 and emitting the character E, transitioning to state 2 and emitting the character ME, transitioning to state 1 and emitting the character M, transitioning to state 1 and emitting the character B, transitioning to state 1 and emitting the character E, transitioning to state 3 and emitting the character REVER, transitioning to state 3 and emitting the character REVER, transitioning to state 1 and emitting the character S, transitioning to state 1 and emitting the character E, transitioning to state 1 and emitting the character M, transitioning to state 2 and emitting the character ER, transitioning to state 1 and emitting the character E, transitioning to state 1 and emitting the character V, transitioning to state 2 and emitting the character ER, transitioning to state 1 and emitting the character B, transitioning to state 1 and emitting the character S.

Task 2: Gene Finding (on one strand of a genome)

In this task, you will use the HMM from Task 1 to predict genes in genomic sequences. Even if you didn't complete Task 1, you can still complete Task 2 by using the provided sample solution HMM implementation, HMM_Sols.

Consider the four state HMM shown in the image below:

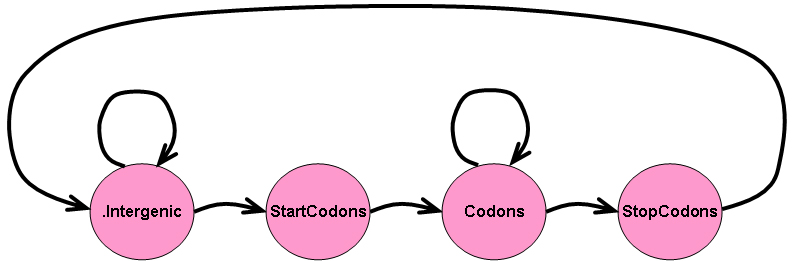
In the above HMM, the .Intergenic state corresponds to intergenic (non-coding) regions of a genome, the StartCodons state corresponds to the start codons of genes (usually ATG but occasionally others such as TTG, CTG, GTG, ATT, CGA, ACG, or AGT, depending on the organism), the Codons state corresponds to the 64 codons found in genes (not counting the start or stop codons of the genes), and the StopCodons state corresponds to the stop codons of genes (usually TAA, TGA, and TAG, but occasionally others such as AGA, AGG, or GGA, depending on the organism).

Suppose we want to use the above HMM to predict genes in a genomic sequence from the bacteria Escherichia coli. First, we would need to determine the parameters of the HMM. For example, what is the probability of emitting different nucleotides from each of the four states? If we have reason to believe that the GC-content of intergenic regions in E. coli is about 44%, we might set the probability of emitting nucleotide G or C in the .Intergenic state to be 0.22 each, and the probability of emitting nucleotide A or T to be 0.28 each. Similarly, if we have reason to believe that the stop codon used by E. coli is TAA for 65% of its genes, TGA for 28% of its genes, and TAG for 7% of its genes, then we might set the probability of emitting nucleotides TAA, TGA, and TAG in the StopCodons state to be 0.65, 0.28, and 0.07, respectively. The file Ecoli_states.txt specifies one possible set of reasonable emission probabilities for each of the four states. We would also need to determine the probability of transitioning from each of the four states to any other of the four states. For example, since approximately 99.4% of intergenic nucleotides in the E. coli genome are followed by another intergenic nucleotide and only 0.6% of intergenic nucleotides are followed in the genome by a protein-coding nucleotide (i.e., the first nucleotide of a gene's start codon), we might set the probability of transitioning from the .Integenic state to the .Intergenic state to be 0.994 and the probability of transitioning from the .Intergenic state to the StartCodons state to be 0.006. The file Ecoli_transitions.txt specifies one possible set of reasonable transition probabilities for the four states.

Once parameters of the HMM are determined, for a given genomic sequence (i.e., observation sequence), the HMM can then be used to predict genes in the genomic sequence by computing the optimal annotation of the genomic sequence. Any nucleotides emitted from one of the three codon states in the optimal annotation are predicted to be protein-coding gene regions and any nucleotides emitted from the .Intergenic state in the optimal annotation are predicted not to be protein-coding gene regions. For instance, if we want to predict whether there are any genes in the first 290 nucleotides of the E. coli genome, as specified in the file Ecoli_observation_290.txt, we can use the HMM to determine the optimal annotation of this 290 nucleotide observation sequence. Based on the model parameters specified in the files Ecoli_states.txt and Ecoli_transitions.txt, the optimal annotation of the 290 nucleotide observation sequence is: 


Optimal annotation:

                AGCTTTTCATTCTGACTGCAACGGGCAATATGTCTCTGTGTGGATTAAAAAAAGAGTGTC    60
                ............................................................

                TGATAGCAGCTTCTGAACTGGTTACCTGCCGTGAGTAAATTAAAATTTTATTGACTTAGG    120
                ............................................................

                TCACTAAATACTTTAACCAATATAGGCATAGCGCACAGACAGATAAAAATTACAGAGTAC    180
                ............................................................

                ACAACATCCATGAAACGCATTAGCACCACCATTACCACCACCATCACCATTACCACAGGT    240
                .........SSSCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC

                AACGGTGCGGGCTGACGCGTACAGGAAACACAGAAAAAAGCCCGCACCTG      290
                CCCCCCCCCCCCSSS...................................


Score of optimal annotation:    -394.77759698115904

In the optimal annotation above, nucleotides with a period, ., below them correspond to the .Intergenic state (note that the first character in the name of the .Intergenic state is a period). Nucleotides with the letter S below them correspond either to the StartCodons or StopCodons state (the names of both states start with the letter S), and nucleotides with a C below them correspond to the Codons state. In the case of the optimal annotation above, the predicted protein-coding nucleotides correspond precisely to those of a documented gene, the thr operon leader peptide, in the E. coli genome known to reside between nucleotides 190 and 255 in the genome.

Of course, we could predict genes (i.e., determine the optimal annotation) in much longer genomic sequences (i.e., observation sequences) as well. We could predict genes throughout the E. coli genome. If we want to predict genes in genomic sequences from other organism besides E. coli, we can do so as long as we have reasonable sets of model parameters (emission probabilities and transition probabilities). The model parameters should be genome specific because different genomes have different GC-contents, have different affinities for codons, and have different densities of genes within their genomes.

With the code available to download on the CS server, we have provided you with several files in the data_OneStrand directory. These files contain reasonable model parameters (emission and transition probabilities) for E.coli, for Yeast, for Arabidopsis, and for Fly genomes. Using these files and the observation sequence files in the data_OneStrand directory, you should predict genes throughout:

By default, the HMM application outputs the optimal annotation of an observation sequence to the screen as well as to a file named annotation.txt. For large genome sequences, your program may be slow to output the annotation to the screen, so you may want to comment out the lines in the main method that print the annotation to the screen (you only really need the file, annotation.txt).

Once you have predicted genes in a genomic sequence, it would useful to evaluate how accurate the predictions are. In the data_OneStrand directory that you downloaded, there are files listing the known genes in E. coli, Yeast, Arabidopsis, and Fly. The provided application EvaluateGenePredictions will allow you to compare your gene predictions to the known genes and assess the accuracy of your predictions. You can find the contract for the EvaluateGenePredictions class here. The EvaluateGenePredictions class reports the sensitivity and specificity of predictions. The sensitivity is the percent of documented coding nucleotides that are correctly predicted as coding nucleotides. The specificity is the percent of documented non-coding (i.e., intergenic) nucleotides that are correctly predicted as non-coding nucleotides.

In the first four rows of the Table of Results, please fill in the sensitivity and specificity of your gene predictions based on the four-state HMM for E. coli, Yeast, Arabidopsis, and Fly.

Task 3: Gene Finding (on both strands of a genome)

The four-state HMM described in Task 2 only predicts genes on one strand of a genomic sequence. Of course, to predict genes on both strands of a genomic sequence, we could always predict genes on one strand of the sequence and then create a second sequence that is the reverse complement of the first and then predict genes on the second sequence. However, a better approach may be to use a HMM that predicts genes along both strands simultaneously.

Consider the seven state HMM shown in the image below:

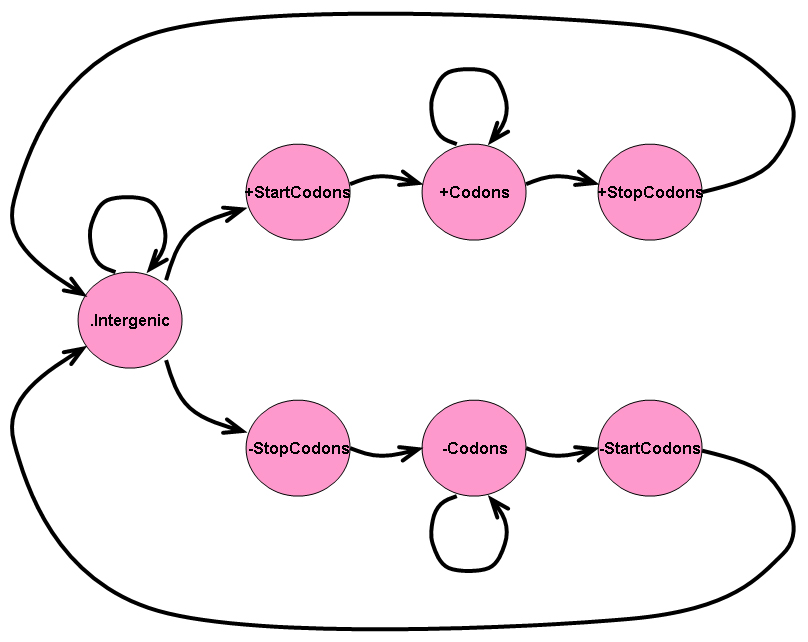
If we were searching for genes along one strand, call it the "+" strand, of a genomic sequence, we would look for a start codon followed by a series of codons followed by a stop codon. If we were searching for genes that resided on the opposite strand, call it the "-" strand, of a genomic sequence, we would look for the reverse complement of a stop codon followed by the reverse complement of a series of codons followed by the reverse complement of a start codon. The seven state HMM above is meant to reflect a HMM that can search for genes along both strands of a genomic sequence simultaneously.

Using the model parameter (emission and transition probabilities) files in the data_OneStrand directory as a starting point, you should create new model parameter (emission and transition probabilities) files corresponding to the seven state HMM depicted above. You should create new model parameter files for E. coli, for Yeast, for Arabidopsis, and for Fly. You should store these new files in the directory data_TwoStrand. Once you have created these model parameter files, you should predict genes throughout:

Use the EvaluateGenePredictions application to assess your gene predictions. In rows five through eight of the Table of Results, please fill in the sensitivity and specificity of your gene predictions based on the seven-state HMM for E. coli, Yeast, Arabidopsis, and Fly.

Task 4: Gene Finding (on both strands of a genome with introns)

The seven-state HMM described in Task 3 only predicts genes that have continuous coding regions. Such a model will work well for bacteria, which do not have introns and exons as part of their genes. However, for eukaryotes, genes are often split into protein-coding exons and non-coding introns. Ideally, we would like our HMM to be able to predict genes that contain exons and introns.

Consider the thirteen state HMM shown in the image below:

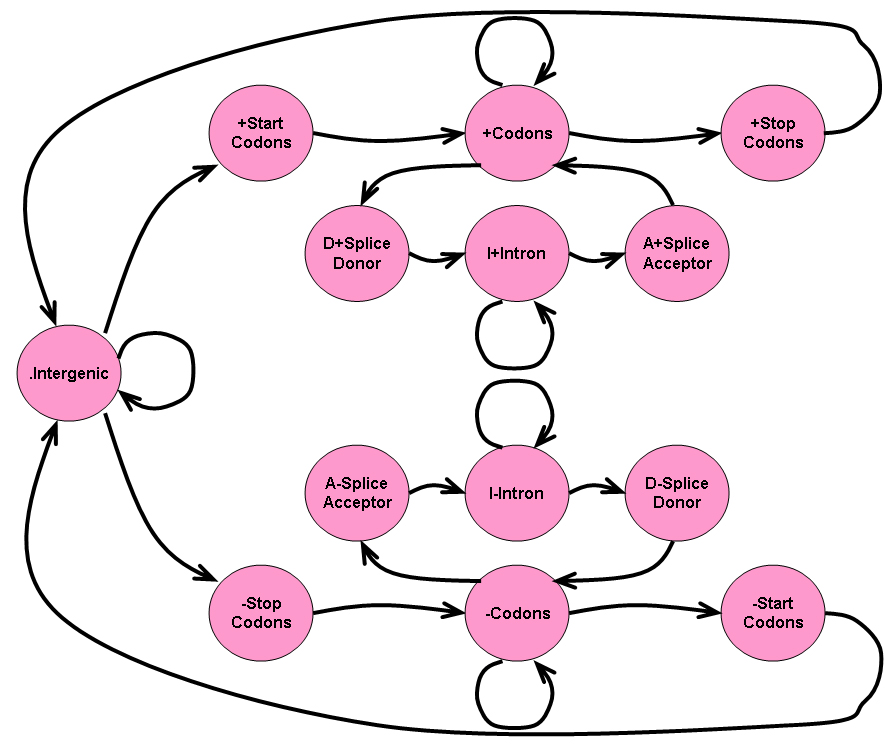
The HMM depicted above is meant to model genes that may have exons and introns. In the model above, a coding region (a series of codons) may be broken up by introns (sequences of non-coding nucleotides).

For the model above, we will make a few simplifying assumptions:

For this task, your goal is to create new model parameter (emission and transition probabilities) files corresponding to the thirteen state HMM depicted above. You should create new model parameter files for E. coli, for Yeast, for Arabidopsis, and for Fly. You should store these new files in the directory data_TwoStrandIntron. When developing your model parameter files, think about how you can use the simplifying assumptions described above. As an example to help you think about the transition probabilities out of a state:

Once you have created the model parameter files, you should predict genes throughout:

Use the EvaluateGenePredictions application to assess your gene predictions. In rows nine through twelve of the Table of Results, please fill in the sensitivity and specificity of your gene predictions based on the thirteen-state HMM for E. coli, Yeast, Arabidopsis, and Fly.