Take-Home Exam 1
-
Due: 2:30am Tuesday, March 8, 2016. This is a hard deadline.
-
Overview: This is a week-long take-home exam. It has 6 problems, most of which require writing Racket programs. The number of points for each problem and subproblem appear in parentheses next to the problem. There are 100 points total on the exam. The problems are independent of one another, and you can do them in any order you find convenient. Even the subproblems have been designed so that you can do them in any order.
- Exam Policy: This exam is open book, in the sense that you can consult any books, handouts, or online materials to solve the problems, subject to the restrictions specified below. However:
- You may not consult solutions for exams or problem sets used in previous semesters of CS251.
- The only person you may talk with about the exam is Lyn. If you ask a question about the exam and I decide that I can answer it, we will send an email with the question and answer to the whole class.
- You may not communicate in any way with any other person (including course tutors and other students taking this course) about any aspect of this exam.
- Although you may consult the Internet for general documentation and tutorials on Racket and programming language concepts, you are not allowed to search the Internet for specific answers to the problems on this exam, and you are not allowed to ask questions on any forum about this exam.
- Except for helper functions provide in this exam itself, you must write all code on your own.
- If you have any questions about what is and is not allowed on this exam, ask Lyn.
- By submitting the exam, you acknowledge that you have followed this exam policy. Any violations of this policy will be brought before the Honor Code Council. In the past, violations of this policy have resulted in failing the course and even expulsion.
-
Starting the Exam:
-
Click on this link to exam1-starter.rkt to download a file with starter code for this exam.
-
Rename the downloaded file to
yourAccountName-exam1.rkt. Write all of your Racket code in this file at the spots where the comments indicate you should write it. -
In the yourFullName CS251 Spring 2016 Folder that you created for PS1, create a Google Doc named yourFullName CS251 Exam1.
-
Include all answers, including copies of code from your
.rktfile in your Exam1 google doc.
-
- Notes:
-
The problems needn’t be done in order. Feel free to jump around.
-
For each problem and subproblem, please indicate at the beginning of each writeup approximately how long that problem took you to solve and write up.
-
Changes to problem description wording from the original exam will be highlighted in magenta.
-
-
Submission:
- Drop your
yourAccountName-exam1.rktfile in your~/cs251/drop/exam1drop folder on cs.wellesley.edu. - Verify that your yourFullName CS251 Exam1 document is shared with Lyn, Sara, and Sravanti.
- Drop your
1. Conjunction Junction (10 points)
We have seen that Racket’s and is not a function, but syntactic sugar. For example, if exp1 and exp2 are expressions, (and exp1 exp2 ) desugars to (if exp1 exp2 #f).
Suppose we define a function and-fun as follows:
(define (and-fun a b) (if a b #f))Although and and and-fun seem similar, there are some subtle but important differences between them.
-
(8 points) For each of the following three function definitions using
and, explain whether the defined functions would or would not have exactly the same behavior ifandwere replaced byand-fun. In this problem ``behavior’’ not only means the input/output behavior of the function, but also how much work it does (i.e., how many operations does it perform?) Explain each answer. In cases where behaviors are different, give one or more concrete examples in which the two versions behave differently, and explain why they behave differently.(define (between x lo hi) (and (<= lo x) (<= x hi))) (define (first-positive? nums) (and (not (null? nums)) (> (first nums) 0))) (define (all-negative? nums) (foldr and #t (map (λ (n) (< n 0)) nums)))Note:
-
The original
all-positive?function was problematic has been replaced by thefirst-positive?function. -
The
all-negative?function above has a syntax error, but that is intentional. Understanding this error is part of the problem. Hint: is there still an error ifandis replaced byand-funinall-negative?
-
-
(2 points) Is Java’s
&&construct more like (1) Racket’sandor (2) theand-funfunction defined above? Briefly explain your answer, using examples as appropriate.
2. It’s a Factor (16 points)
The following least-divisor-rec function correctly returns the least positive integer that evenly divides the given positive integer num.
(define (least-divisor-rec num) ;; Assume num is a postive integer
(let ((limit (ceiling (sqrt num)))) ;; The largest divisor to be tested
(define (search-for-divisor candidate)
(if (> candidate limit)
num
(if (divisible-by? num candidate)
candidate
(search-for-divisor (+ candidate 2)))))
(if (divisible-by? num 2)
2
(search-for-divisor 3))))
(define (divisible-by? num divisor)
(= (remainder num divisor) 0))We can use map with range to test least-divisor-rec on many inputs:
> (map (λ (n) (list n (least-divisor-rec n))) (range 45 56))
'((45 3) (46 2) (47 47) (48 2) (49 7) (50 2) (51 3) (52 2) (53 53) (54 2) (55 5))Using least-divisor-rec, we can define a function factors-rec that returns a list of all primes factors of a given positive integer, sorted from low to high:
(define (factors-rec num)
(let ((factor (least-divisor-rec num)))
(if (= factor num)
(list factor)
(cons factor (factors-rec (quotient num factor))))))
> (map (λ (n) (list n (factors-rec n))) (range 60 73))
'((60 (2 2 3 5))
(61 (61))
(62 (2 31))
(63 (3 3 7))
(64 (2 2 2 2 2 2))
(65 (5 13))
(66 (2 3 11))
(67 (67))
(68 (2 2 17))
(69 (3 23))
(70 (2 5 7))
(71 (71))
(72 (2 2 2 3 3)))-
(3 points) Using
factors-recin conjunction with the higher-orderforall?function we defined in class (it is one of your given helper functions), it is possible to give a very simple definition of thehamming?function from PS2. Flesh out this skeleton ofhamming?:(define (hamming? num) (and (integer? num) (> num 0) (or (= num 1) (forall? ; put expression 1 here ; put expression 2 here )) > (filter hamming? (range 0 101)) '(1 2 3 4 5 6 8 9 10 12 15 16 18 20 24 25 27 30 32 36 40 45 48 50 54 60 64 72 75 80 81 90 96 100) -
(4 points) Using the higher-order
findfunction we defined in class (it is one of your given helper functions), it is possible to define a functionleast-divisor-findthat searches through the same candidates to return the same answer asleast-divisor-recfor every positive integer input. Flesh out this skeleton ofleast-divisor-find:(define (least-divisor-find num) (find ; put expression 1 here ; put expression 2 here ; put expresion 3 here )) > (map (λ (n) (list n (least-divisor-find n))) (range 45 56)) '((45 3) (46 2) (47 47) (48 2) (49 7) (50 2) (51 3) (52 2) (53 53) (54 2) (55 5))Notes:
-
Your definition of
least-divisor-findshould use the same algorithm asleast-divisor-recto find the least divisor. In particular, it should search through exactly the same candidates thatleast-divisor-recsearches through. -
For generating candidate divisors, it is helpful to know that the Racket
rangefunction (like the Pythonrangefunction) takes an optional thirdstepargument that is added to the current number to determine the next one. (The default step is 1.) For example:> (range 1 20 3) '(1 4 7 10 13 16 19) -
You are not allowed to use
factors-recin your definition ofleast-divisor-rec. -
least-divisor-findshould perform thedivisible-by?test on exactly the same candidates asleast-divisor-rec. -
(least-divisor-find n)may take time proportional to the square root of n, even in cases whereleast-divisor-recwould return after a small number of steps (e.g., when n is an even number.)
-
-
(4 points) Using the higher-order
genlistfunction we defined in class (it is one of your given helper functions), it is possible to define a functionfactors-genlistthat behaves likefactors-recfor every positive integer input. Flesh out the following skeleton offactors-genlist. You may useleast-divisor-recin your definition.(define (factors-genlist num) (map second (genlist ; put expression 1 here ; put expression 2 here (list num ; put expression 3 here )))) > (map (λ (n) (list n (factors-genlist n))) (range 60 73)) '((60 (2 2 3 5)) (61 (61)) (62 (2 31)) (63 (3 3 7)) (64 (2 2 2 2 2 2)) (65 (5 13)) (66 (2 3 11)) (67 (67)) (68 (2 2 17)) (69 (3 23)) (70 (2 5 7)) (71 (71)) (72 (2 2 2 3 3))) -
(5 points) Using the higher-order
iterate-applyfunction we defined in class (it is one of your given helper functions), it is possible to define a functionfactors-iterate-applythat behaves likefactors-recfor every positive integer input. Flesh out the following skeleton offactors-iterate-apply. You may useleast-divisor-recandreversein your definition.(define (factors-iterate-apply num) (iterate-apply ; put expression 1 here ; put expression 2 here ; put expression 3 here (list num null))) > (map (λ (n) (list n (factors-iterate-apply n))) (range 60 73)) '((60 (2 2 3 5)) (61 (61)) (62 (2 31)) (63 (3 3 7)) (64 (2 2 2 2 2 2)) (65 (5 13)) (66 (2 3 11)) (67 (67)) (68 (2 2 17)) (69 (3 23)) (70 (2 5 7)) (71 (71)) (72 (2 2 2 3 3)))
3. Mysterious Composition (18 points)
This problem involves the following mystery function:
(define (mystery nums)
(foldr max 0
(filter (λ (n) (> n 0))
(map (λ (pair) (* (car pair) (cdr pair)))
((λ (ns) (zip ns (rest ns)))
(cons 0 nums))))))-
(3 points) Explain in English what the
mysteryfunction does. Do not explain in words the Racket code or algorithm. Rather, describe a high-level specification for the output ofmysteryfor its input. -
(1 point) Explain why the last subexpression is
(cons 0 nums)rather thannums. -
(4 points) Using Racket’s
foldl, we can define a functionmystery-foldlthat has the same input/output behavior asmystery. Flesh out the following skeleton ofmystery-foldl:(define (mystery-foldl nums) (cdr (foldl ; put combiner expression here (cons 0 0) ; pair of (1) previous list value and (2) maximum so far nums))) -
(2 points) Describe two advantages of
mystery-foldlvs.mystery. -
(8 points) Here are some helper functions useful for expressing functions in a compositional style:
(define (id x) x) (define (o f g) (λ (x) (f (g x)))) (define (o-all fun-list) (foldr o id fun-list)) (define (flip2 binop) (λ (x y) (binop y x))) (define (curry2 binop) (λ (x) (λ (y) (binop x y)))) (define (curry3 ternop) (λ (x) (λ (y) (λ (z) (ternop x y z))))) (define (pair-dup x) (cons x x)) (define (pair-apply f g) (λ (pair) (cons (f (car pair)) (g (cdr pair))))) (define (unpair-apply binop) (λ (pair) (binop (car pair) (cdr pair))))You have seen the first six functions before, but the last three (
pair-dup,pair-apply, andunpair-apply) are new.Give an alternative definition of
mysterythat has the following pattern, where each of the functions<fun_1>through<fun_k>is expressed without using any explicitlambdas:(define mystery-composed (o-all (list <fun_1> ... <fun_k>)))Notes:
-
In your definition, use the helper functions at the beginning of this part in addition to
foldr,filter,map, andzip. -
If you are unable to remove all
lambdas, remove as many as you can for partial credit.
-
4. Folding (15 points)
-
(3 points) Python has a
reduceoperator that is a folding-like operator. (You may look up documentation for Python’sreduceon the interwebz.) Is it closer tofoldrorfoldl? Briefly but carefully justify your answer. -
(5 points) Using
foldr, define a function(unzip pairs)that takes a list of pairs (cons cells) and returns a list of two lists that, if zipped together withzip, would yield the original pairs.> (unzip (zip (list 1 2 3 4) (list 5 6 7 8))) '((1 2 3 4) (5 6 7 8)) > (unzip (list)) '(() ())Your definition should flesh out the following skeleton:
(define (unzip pairs) (foldr ; put expression 1 here ; put expression 2 here pairs))Note:
- This is very similar to the divide-conquer-glue recursions from PS2 and
foldrexamples from PS3. Keep in mind that your function needs to produce only one of the potential solutions like those shown above.
- This is very similar to the divide-conquer-glue recursions from PS2 and
-
(7 points) Suppose that we represent a set in Racket as a list without duplicates. Using
foldr, define a function(subsets set)that returns a list of all subsets of a given set. The subsets within this can be in any order, but the order of elements within each set should have the same relative order as inset.For example here are some of the (huge number of) possible answers for
(subsets (list 3 1 2)), any single one of which would be considered correct:'(() (1) (2) (3) (1 2) (3 1) (3 2) (3 1 2)) '((3 1 2) (3 2) (3 1) (1 2) (3) (2) (1) ()) '(() (2) (1) (1 2) (3) (3 2) (3 1) (3 1 2)) '((3 1 2) () (3 1) (2) (3) (1 2) (1) (3 2))However, lists containing subsets like
(2 1),(1 3),(3 2 1), or(1 2 3)could not be solutions, since the elements of these subsets are not in the same relative order as(3 1 2).Your definition should flesh out the following skeleton, and may use other higher-order operators and standard list combiners (e.g.
append), but may not use any form of list reversal.(define (subsets set) (foldr ; put expression 1 here ; put expression 2 here set))Note:
- This is very similar to the divide-conquer-glue recursions from PS2 and
foldrexamples from PS3. Keep in mind that your function needs to produce only one of the potential solutions like those shown above.
- This is very similar to the divide-conquer-glue recursions from PS2 and
5. Down and Up Recursion (29 points)
We have seen that a list recursion can have both a down phase (in which values may be accumulated as the elements are processed left-to-right) and an up phase (in which values may be accumulated as the elements are processed right-to-left). It is even possible in a single recursion over a list of elements to combine those elements and the intermediate results of the down and up accumulations in interesting ways.
In this problem we will consider a function (down-and-up nums) that is an example of such a list recursion over a list of integers nums.
To understand what down-and-up does, we’ll define the partial sum list of a list of numbers to be the partial sums of the numbers in a left-to-right summation of the elements. E.g., the partial sum list of '(1 2 3 4 5) is '(1 3 6 10 15), the partial sum list of '(2 4 5 1 3) is '(2 6 11 12 15), and the partial sum list of '(8 2 1 16 4 1) is '(8 10 11 27 31 32).
(down-and-up nums) returns a list of 3 elements:
-
The first element of the resulting list is a list whose elements are the elements of
numsscaled by the corresponding elements of the partial sum list ofnums. For example:- When nums is
'(1 2 3 4 5), the partial sum list is'(1 3 6 10 15), so the scaled list is'(1 6 18 40 75). - When nums is
'(2 4 5 1 3), the partial sum list is'(2 6 11 12 15), so the scaled list is'(4 24 55 12 45). - When nums is
'(8 2 1 16 4 1), the partial sum list is'(8 10 11 27 31 32), so the scaled list is'(64 20 11 432 124 32). - When nums is
'(8 2 17 4 1), the partial sum list is'(8 10 27 31 32), so the scaled list is'(64 20 459 124 32).
- When nums is
-
The second element of the resulting list is the sum of the elements in
nums. For example, both'(1 2 3 4 5)and'(2 4 5 1 3)have sum15, while'(8 2 1 16 4 1)has sum32. -
The third element of the resulting list is a list of booleans that indicate which elements of
numsevenly divide the sum of the elements innums. For example:- When nums is
'(1 2 3 4 5), the boolean list is'(#t #f #t #f #t), because 1, 3, and 5 divide 15 but 2 and 4 do not. - When nums is
'(2 4 5 1 3), the boolean list is'(#f #f #t #t #t)for the same reason. - When nums is
'(8 2 1 16 4 1), the boolean list is'(#t #t #t #t #t #t)because all of the elements divide 32.
- When nums is
So here are examples of down-and-up:
> (down-and-up '(1 2 3 4 5))
'((1 6 18 40 75) 15 (#t #f #t #f #t))
> (down-and-up '(2 4 5 1 3))
'((4 24 55 12 45) 15 (#f #f #t #t #t))
> (down-and-up '(8 2 1 16 4 1))
'((64 20 11 432 124 32) 32 (#t #t #t #t #t #t))
> (down-and-up '(8 2 12 4 6))
'((64 20 264 104 192) 32 (#t #t #f #t #f))
> (down-and-up '(8 2 17 4 1))
'((64 20 459 124 32) 32 (#t #t #f #t #t)) ; This has been corrected from an earlier incorrect answer-
(9 points) Define the
down-and-upfunction by fleshing out the skeleton of thedown-and-up-helperfunction in the following sekeleton. Yourdown-and-up-helperfunction should be recursive and should make only one pass over the list. You should not use any higher-order list functions or any helper functions other thandivisible-by?in your definition.(define (down-and-up nums) (down-and-up-helper 0 nums)) (define (down-and-up-helper sumSoFar ns) (if (null? ns) ; put expression 1 here ; put expression 2 here ))Notes:
-
You should not need to use any list operators other than
first,second,third,rest,cons, andlist. In particular,appendis not necessary. (Note:secondandthirdwere recently added to the list.) -
Your definition should make exactly one recursive call to
down-and-up-helper; otherwise it would make more than one pass over the list. Also, if there is more than one such call, the definition will suffer from the problem withbad-maxlistshown in slides 9-17 through 9-19 of the slides on Local Naming and Scope. Using the strategy forgood-maxlistin slide 9-20, this problem can be solved by having only a single recursive call. Note: you will still get substantial partial credit in this problem if there are multiple recursive calls todown-and-up-helper. -
Below is an image showing all the operations that are performed in (down-and-up-helper 0 ‘(1 2 3 4 5)). Click here for a sequence of images animating the down and up phases of
down-and-up-helperin this example.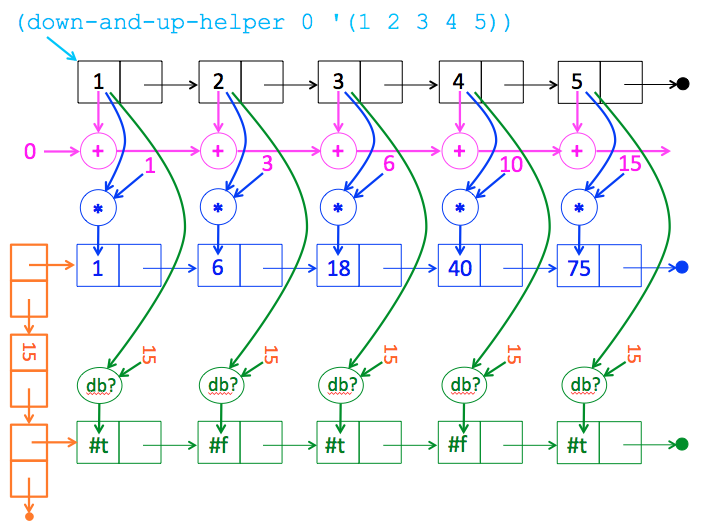
-
In the twelve images of the sequence, there are six calls to
down-and-up-helper. Two images are shown for each such call: one for the state of the system when the call is made, and one for the state of the system when it returns. I have modified the return slides to show the return value. Here are the six calls and their results. You can use these as six test cases fordown-and-up-helper:> (down-and-up-helper 15 '()) '(() 15 ()) > (down-and-up-helper 10 '(5)) '((75) 15 (#t)) > (down-and-up-helper 6 '(4 5)) '((40 75) 15 (#f #t)) > (down-and-up-helper 3 '(3 4 5)) '((18 40 75) 15 (#t #f #t)) > (down-and-up-helper 1 '(2 3 4 5)) '((6 18 40 75) 15 (#f #t #f #t)) > (down-and-up-helper 0 '(1 2 3 4 5)) '((1 6 18 40 75) 15 (#t #f #t #f #t))
-
-
(6 points) We can generalize
down-and-upinto a higher-order list functionfoldLRthat has aspects of bothfoldlandfoldr. The lettersLRat the end offoldLRhave been capitalized to emphasize them; since Racket identifiers are case-sensitive, they must be capitalized.(define (foldLR combineL state combineR nullfun xs) (if (null? xs) (nullfun state) (let ((next-state (combineL (car xs) state))) (combineR (first xs) next-state (foldLR combineL next-state combineR nullfun (rest xs))))))Give an alternative definition of
down-and-upnameddown-and-up-foldLRthat is implemented in terms offoldLRby fleshing out this skeleton:(define (down-and-up-foldLR nums) (foldLR ; put expression 1 here ; put expression 2 here ; put expression 3 here ; put expression 4 here nums))Notes:
-
To understand
foldLR, it may be helpful to review the definitions ofmy-foldrfrom slide 6-24 of the First-Class Functions in Racket slides and the definition ofmy-foldlfrom slide 8-25 of the Iteration Via Tail Recursion slides.foldLR’scombineLandstatecorrespond tocombinerandresultSoFarinmy-foldlfoldLR’scombineRandnullfunare generalizations ofcombineandnullvalinmy-foldr
-
In both parts 5b and 5c, keep in mind that it is often useful for a function to ignore one or more of its arguments. For example, consider the following:
(define (return17 x) 17) ; ignores argument and always returns 17 (define (add-first-and-last x y z) (+ x z)) ; ignores middle argument (define (foldr-ternop ternop null-value xs) ; standard definition of foldr-ternop from PS3 (if (null? xs) null-value (ternop (car xs) (cdr xs) (foldr-ternop ternop null-value (cdr xs))))) > (return17 42) 17 > (map return17 (range 10)) '(17 17 17 17 17 17 17 17 17 17) > (add-first-and-last 1 20 300) 301 > (foldr-ternop add-first-and-last 0 (list 1 2 3 4)) 10 ; = 1 + 2 + 3 + 4 ; add-first-and-last ignore the second argument in the combiner of foldr-ternop
-
-
(12 points) Define versions of
foldl,foldr, andfoldr-ternop(this last one from PS3) in terms offoldLRby fleshing out the following skeletons:(define (my-foldl combine state xs) (foldLR ; put expression 1 here ; put expression 2 here ; put expression 3 here ; put expression 4 here xs)) (define (my-foldr combine nullval xs) (foldLR ; put expression 1 here ; put expression 2 here ; put expression 3 here ; put expression 4 here xs)) (define (my-foldr-ternop ternop nullval xs) (foldLR ; put expression 1 here ; put expression 2 here ; put expression 3 here ; put expression 4 here xs))For example:
> (my-foldl cons (list) (list 1 2 3 4)) '(4 3 2 1) > (my-foldr cons (list 17) (list 1 2 3 4)) '(1 2 3 4 17) > (my-foldr-ternop (λ (fst rst subres) (cons (list fst rst) subres)) (list) (list 1 2 3 4)) '((1 (2 3 4)) (2 (3 4)) (3 (4)) (4 ()))Notes:
-
The idea here is that
foldLRis a generalization of bothfoldlandfoldr, and by passing it appropriate arguments, you can make it behave likefoldl,foldr, andfoldr-ternopin addition to expressing more complicated functions likedown-and-up. -
See the note in 5b about functions that ignore one or more of their arguments.
-
-
(2 points) After you define
my-foldlin terms offoldLR, you fall asleep and are visited in a dream by a spirit that calls itself “The Great Quux”. It tells you that a correctly-definedmy-foldlwill often return the same results asfoldl, but will fail to act likefoldlin a fundamental respect. You wake up in a cold sweat and realize the spirit is correct. Explain.
6. Losing Your Marbles (12 points)
Assume that m is a nonnegative integer and that c is a positive integer. Given m marbles and a row of c cups, (marbles m c) returns a sorted list of all configurations whereby all m marbles are distributed among the c cups. Each configuration should be a list of length c whose elements are integers between 0 and m and the sum of whose elements is m. The returned list should be ordered lexicographically (i.e., in dictionary order).
At the end of this problem description are numerous sample invocations of the marbles function.
In Racket, define the marbles function so that it satisfies the above specification and has the same behavior as the sample invocations.
Notes:
-
As usual, you should use divide/conquer/glue as your problem-solving strategy. Strive to make your solution as simple as possible. For example, do not use more base cases than are strictly necessary.
-
You are expected to use higher-order list functions where they can simplify your definition.
-
Feel free to define any auxiliary functions you find helpful.
-
Your
marblesfunction should generate the elements in sorted order without calling any kind of sorting function. -
Don’t forget the very powerful notion of “wishful” thinking, in which you blindly apply a recursive function to smaller versions of the same problem and combine their results. Study the examples carefully to see how the result of a call to
marblesis stitched together from the results of calls to “smaller” versions ofmarbles. -
To help you see patterns better, the results of the following calls have been added below:
(marbles 0 1),(marbles 0 2),(marbles 0 3),(marbles 2 3).
> (marbles 0 1)
'((0))
> (marbles 0 2)
'((0 0))
> (marbles 0 3)
'((0 0 0))
> (marbles 1 1)
'((1))
> (marbles 1 2)
'((0 1) (1 0))
> (marbles 1 3)
'((0 0 1) (0 1 0) (1 0 0))
> (marbles 2 1)
'((2))
> (marbles 2 2)
'((0 2) (1 1) (2 0))
> (marbles 2 3)
'((0 0 2) (0 1 1) (0 2 0) (1 0 1) (1 1 0) (2 0 0))
> (marbles 3 1)
'((3))
> (marbles 3 2)
'((0 3) (1 2) (2 1) (3 0))
> (marbles 3 3)
'((0 0 3) (0 1 2) (0 2 1) (0 3 0) (1 0 2) (1 1 1) (1 2 0) (2 0 1) (2 1 0) (3 0 0))
> (marbles 3 4)
'((0 0 0 3)
(0 0 1 2)
(0 0 2 1)
(0 0 3 0)
(0 1 0 2)
(0 1 1 1)
(0 1 2 0)
(0 2 0 1)
(0 2 1 0)
(0 3 0 0)
(1 0 0 2)
(1 0 1 1)
(1 0 2 0)
(1 1 0 1)
(1 1 1 0)
(1 2 0 0)
(2 0 0 1)
(2 0 1 0)
(2 1 0 0)
(3 0 0 0))
> (marbles 4 1)
'((4))
> (marbles 4 2)
'((0 4) (1 3) (2 2) (3 1) (4 0))
> (marbles 4 3)
'((0 0 4)
(0 1 3)
(0 2 2)
(0 3 1)
(0 4 0)
(1 0 3)
(1 1 2)
(1 2 1)
(1 3 0)
(2 0 2)
(2 1 1)
(2 2 0)
(3 0 1)
(3 1 0)
(4 0 0))
> (marbles 4 4)
'((0 0 0 4)
(0 0 1 3)
(0 0 2 2)
(0 0 3 1)
(0 0 4 0)
(0 1 0 3)
(0 1 1 2)
(0 1 2 1)
(0 1 3 0)
(0 2 0 2)
(0 2 1 1)
(0 2 2 0)
(0 3 0 1)
(0 3 1 0)
(0 4 0 0)
(1 0 0 3)
(1 0 1 2)
(1 0 2 1)
(1 0 3 0)
(1 1 0 2)
(1 1 1 1)
(1 1 2 0)
(1 2 0 1)
(1 2 1 0)
(1 3 0 0)
(2 0 0 2)
(2 0 1 1)
(2 0 2 0)
(2 1 0 1)
(2 1 1 0)
(2 2 0 0)
(3 0 0 1)
(3 0 1 0)
(3 1 0 0)
(4 0 0 0))
> (marbles 5 1)
'((5))
> (marbles 5 2)
'((0 5) (1 4) (2 3) (3 2) (4 1) (5 0))
> (marbles 5 3)
'((0 0 5)
(0 1 4)
(0 2 3)
(0 3 2)
(0 4 1)
(0 5 0)
(1 0 4)
(1 1 3)
(1 2 2)
(1 3 1)
(1 4 0)
(2 0 3)
(2 1 2)
(2 2 1)
(2 3 0)
(3 0 2)
(3 1 1)
(3 2 0)
(4 0 1)
(4 1 0)
(5 0 0))
> (marbles 5 4)
'((0 0 0 5)
(0 0 1 4)
(0 0 2 3)
(0 0 3 2)
(0 0 4 1)
(0 0 5 0)
(0 1 0 4)
(0 1 1 3)
(0 1 2 2)
(0 1 3 1)
(0 1 4 0)
(0 2 0 3)
(0 2 1 2)
(0 2 2 1)
(0 2 3 0)
(0 3 0 2)
(0 3 1 1)
(0 3 2 0)
(0 4 0 1)
(0 4 1 0)
(0 5 0 0)
(1 0 0 4)
(1 0 1 3)
(1 0 2 2)
(1 0 3 1)
(1 0 4 0)
(1 1 0 3)
(1 1 1 2)
(1 1 2 1)
(1 1 3 0)
(1 2 0 2)
(1 2 1 1)
(1 2 2 0)
(1 3 0 1)
(1 3 1 0)
(1 4 0 0)
(2 0 0 3)
(2 0 1 2)
(2 0 2 1)
(2 0 3 0)
(2 1 0 2)
(2 1 1 1)
(2 1 2 0)
(2 2 0 1)
(2 2 1 0)
(2 3 0 0)
(3 0 0 2)
(3 0 1 1)
(3 0 2 0)
(3 1 0 1)
(3 1 1 0)
(3 2 0 0)
(4 0 0 1)
(4 0 1 0)
(4 1 0 0)
(5 0 0 0))